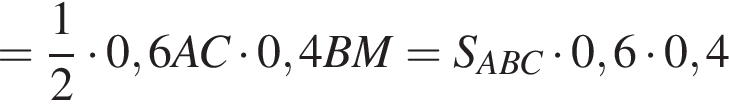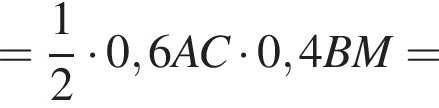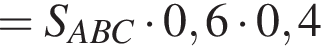Биссектриса CD угла ACB при основании равнобедренного треугольника ABC (AB = AC) делит сторону AB так, что AD = BC = 2.
а) Докажите, что CD = BC.
б) Найдите площадь треугольника ABC.
Решение. а) По свойству биссектрисы получим:

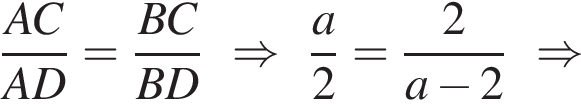
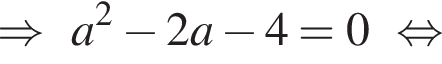

Воспользуемся теоремой синусов для треугольника ABC:
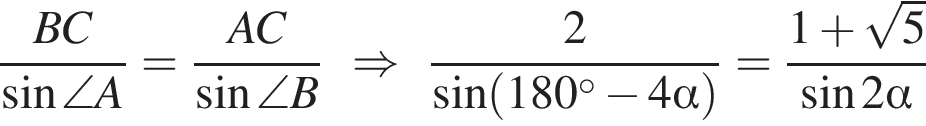






![]()

Осталось по теореме косинусов найти CD из треугольника BCD:


![]()






Таким образом, CD = BC = 2. Что и требовалось доказать.
б) Найдем площадь треугольника по формуле Герона:


![]()


![]()








Ответ: 
Примечание: в данной задаче получилось, что ADC равнобедренный, откуда  откуда
откуда 
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б. | 3 |
| Получен обоснованный ответ в пункте б. ИЛИ Имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. | 2 |
| Имеется верное доказательство утверждения пункта а. ИЛИ При обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. ИЛИ Обоснованно получен верный ответ в пункте б и использованием утверждения пункта а, при этом пункт а не выполнен. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 3 |


 а также
а также  получим:
получим: 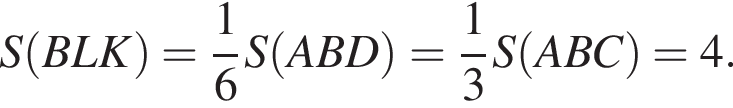
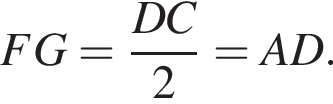 Итак, в четырехугольнике AFGD две стороны равны и параллельны, значит, он параллелограмм и
Итак, в четырехугольнике AFGD две стороны равны и параллельны, значит, он параллелограмм и 
 откуда
откуда 
 откуда
откуда 



 где
где 




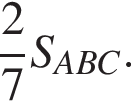




 ) с коэффициентом
) с коэффициентом  ). Значит, и треугольники ACD и BCD подобны.
). Значит, и треугольники ACD и BCD подобны.
 Тогда по теореме Пифагора
Тогда по теореме Пифагора  откуда
откуда 
 и BC = 5. На стороне AB взята точка D такая. что AD = 1.
и BC = 5. На стороне AB взята точка D такая. что AD = 1. откуда
откуда 
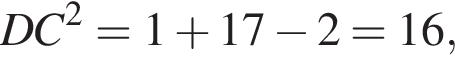 откуда
откуда  и по теореме, обратной к теореме Пифагора, треугольник ADC прямоугольный.
и по теореме, обратной к теореме Пифагора, треугольник ADC прямоугольный.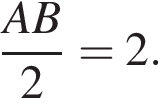
 Рассмотрим два случая, изображенных на рисунке.
Рассмотрим два случая, изображенных на рисунке. находим
находим  а значит,
а значит, 
 то есть
то есть
 Заметим, что второй случай включает в себя первый.
Заметим, что второй случай включает в себя первый. Возможны три варианта.
Возможны три варианта.


 или
или  что невозможно в равнобедренном треугольнике.
что невозможно в равнобедренном треугольнике.


 или
или  откуда углы треугольника равны 30°, 30°, 120°.
откуда углы треугольника равны 30°, 30°, 120°. В этом случае треугольник является равнобедренным прямоугольным, а высота, проведенная к боковой стороне, является боковой стороной и равна 2.
В этом случае треугольник является равнобедренным прямоугольным, а высота, проведенная к боковой стороне, является боковой стороной и равна 2. кроме того,
кроме того, 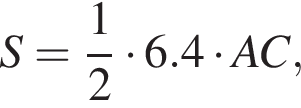 откуда AC = 5.
откуда AC = 5.


 или
или 
 Пусть
Пусть  тогда
тогда 
 так как
так как  Значит,
Значит, 







 поэтому такой случай невозможен.
поэтому такой случай невозможен.









 Значит,
Значит,
 тогда и
тогда и  а по свойству внешнего угла треугольника:
а по свойству внешнего угла треугольника:  Поскольку по условию углы ABD и CAD равны, угол CAD равен 2α. Это значит, что отрезок AB — биссектриса угла CAD, что и требовалось доказать.
Поскольку по условию углы ABD и CAD равны, угол CAD равен 2α. Это значит, что отрезок AB — биссектриса угла CAD, что и требовалось доказать. следовательно,
следовательно, 

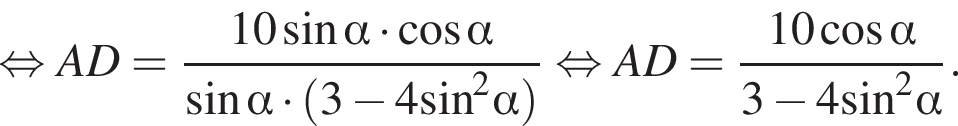
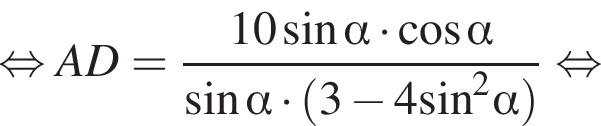



 BE также будет служить высотой этого треугольника. Тогда в прямоугольном треугольнике ABE по теореме Пифагора
BE также будет служить высотой этого треугольника. Тогда в прямоугольном треугольнике ABE по теореме Пифагора  числа 3; 4 и 5 — пифагоровы. Следовательно,
числа 3; 4 и 5 — пифагоровы. Следовательно, 

 Положим
Положим  тогда
тогда  По теореме косинусов для треугольника АВС находим:
По теореме косинусов для треугольника АВС находим:
 Чтобы найти х, используем теорему косинусов для треугольника ADB, подставив найденный косинус угла BAC:
Чтобы найти х, используем теорему косинусов для треугольника ADB, подставив найденный косинус угла BAC:
 откуда
откуда  или
или 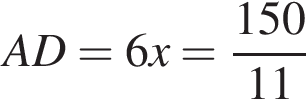 или
или 



 тогда точки лежат в таком порядке A, H, L, M, B.
тогда точки лежат в таком порядке A, H, L, M, B.

 что и требовалось (во втором равенстве использовалось свойство медианы прямоугольного треугольнике).
что и требовалось (во втором равенстве использовалось свойство медианы прямоугольного треугольнике). По свойству биссектрисы треугольника
По свойству биссектрисы треугольника  откуда
откуда  и
и 
 точки
точки  и
и  поэтому указанные треугольники подобны по двум углам.
поэтому указанные треугольники подобны по двум углам. следует, что
следует, что  аналогично
аналогично  поэтому треугольники BAC и BA1C1 подобны с коэффициентом подобия
поэтому треугольники BAC и BA1C1 подобны с коэффициентом подобия  поэтому их площади относятся как
поэтому их площади относятся как 
 тогда
тогда 







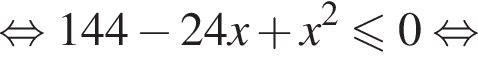
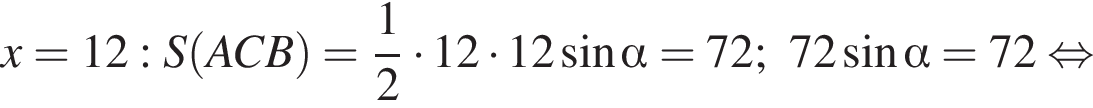

 что и требовалось доказать.
что и требовалось доказать. 
 И пусть MNPQ — упомянутый квадрат
И пусть MNPQ — упомянутый квадрат  Проведем отрезок СО, который пересечет NP в точке K. И пусть b — длина стороны квадрата.
Проведем отрезок СО, который пересечет NP в точке K. И пусть b — длина стороны квадрата. 
 А это значит, что
А это значит, что 


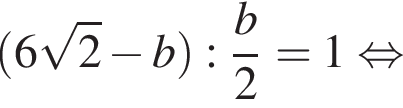

 В ΔCNB:
В ΔCNB:  Откуда:
Откуда: 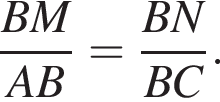
 угол В, заключенный между пропорциональными сторонами, общий. Это значит, что ΔMNB ~ ΔACB, откуда ∠ACB = ∠MNB, что и требовалось доказать.
угол В, заключенный между пропорциональными сторонами, общий. Это значит, что ΔMNB ~ ΔACB, откуда ∠ACB = ∠MNB, что и требовалось доказать.
 то непременно
то непременно 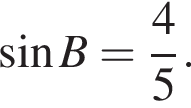 По следствию из теоремы синусов:
По следствию из теоремы синусов: 








































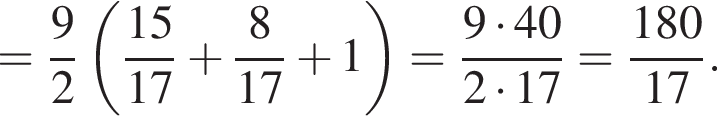





 то
то 

 значит, точка L лежит между M и В.
значит, точка L лежит между M и В. 










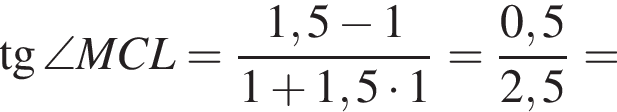
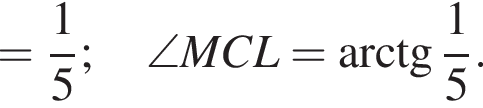



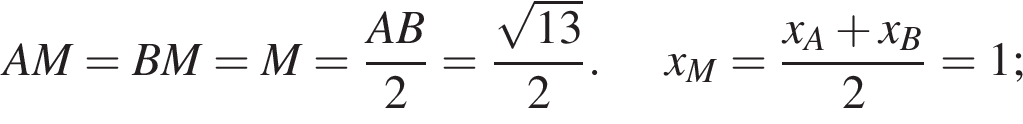








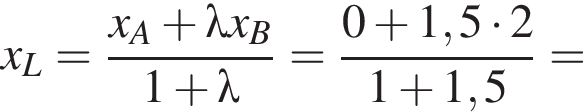










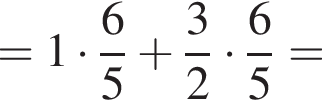









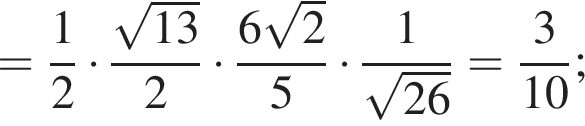



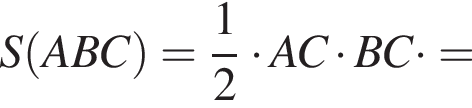






 Будем рассуждать так:
Будем рассуждать так: 
 для заданного треугольника, то цель будет достигнута.
для заданного треугольника, то цель будет достигнута. 




 Тогда диаметр этой окружности d = a + b − c.
Тогда диаметр этой окружности d = a + b − c.
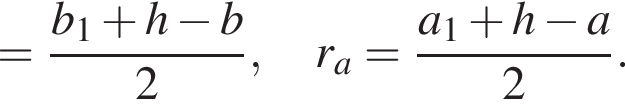




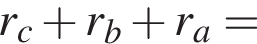
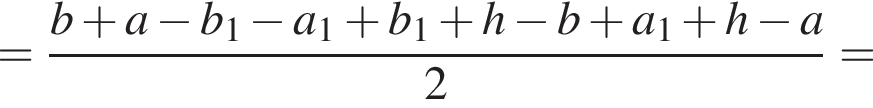



 то
то 
 Кроме того,
Кроме того,  Но по условию задачи известно, что
Но по условию задачи известно, что  значит,
значит,  Тогда:
Тогда: 


 Итак,
Итак, 







 Значит,
Значит, 
 значит:
значит: 



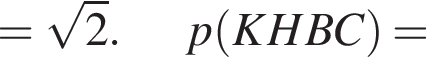






 Пусть отрезки BM и CNделят пополам углы В и С соответственно. Наша задача — доказать, что BM > CN.
Пусть отрезки BM и CNделят пополам углы В и С соответственно. Наша задача — доказать, что BM > CN. Так как этот угол равен углу
Так как этот угол равен углу  то четыре точки
то четыре точки  лежат на одной окружности.
лежат на одной окружности. 



 Следовательно,
Следовательно, 
 т. е. признак равнобедренного треугольника не выполняется. Тогда по лемме 2
т. е. признак равнобедренного треугольника не выполняется. Тогда по лемме 2  что противоречит условию теоремы. Значит, наше предположение о невыполнении равенства
что противоречит условию теоремы. Значит, наше предположение о невыполнении равенства  неверно.
неверно. 
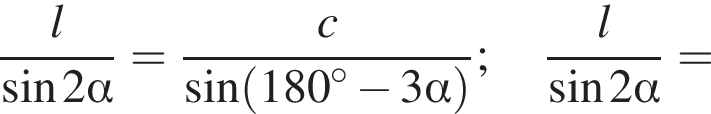


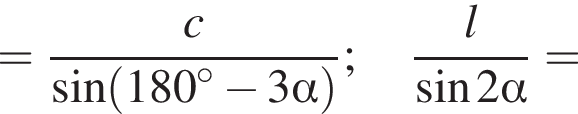








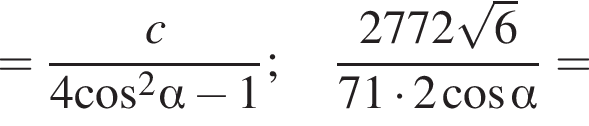
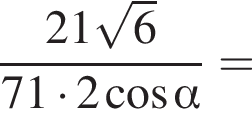






 отрицательное значение
отрицательное значение 








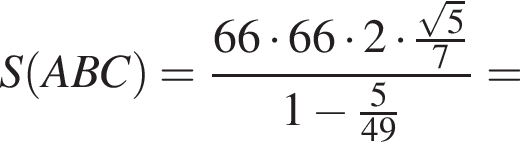




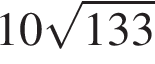 и
и  а площадь треугольника ABC равна
а площадь треугольника ABC равна 



 где h — высота
где h — высота 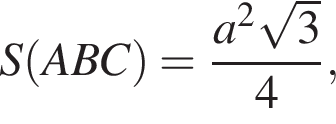 значит,
значит, 






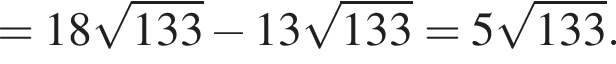

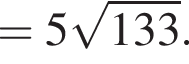

 а высоты треугольника A1B1C1 равны
а высоты треугольника A1B1C1 равны 

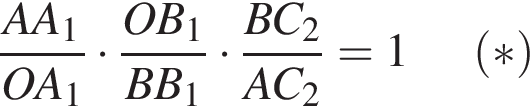

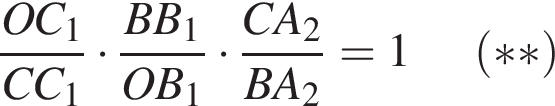
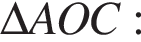


 что удовлетворяет условию теоремы Менелая относительно принадлежности точек:
что удовлетворяет условию теоремы Менелая относительно принадлежности точек:  одной прямой.
одной прямой. — стороны
— стороны  — соответствующие его высоты. Тогда:
— соответствующие его высоты. Тогда: 









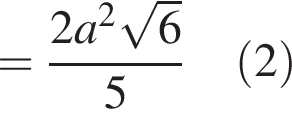
 — стороны
— стороны  При этом
При этом  — соответствующие его высоты. Тогда:
— соответствующие его высоты. Тогда: 




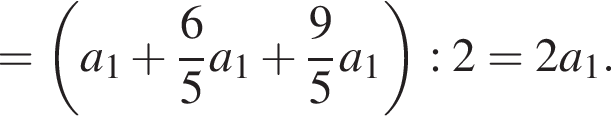



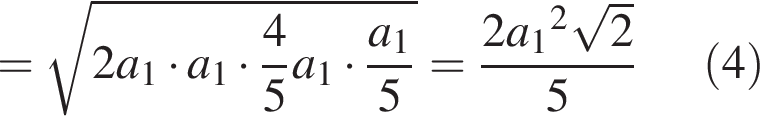









 Следовательно, мы вправе равенство (5) переписать так:
Следовательно, мы вправе равенство (5) переписать так: 
 получим:
получим: 

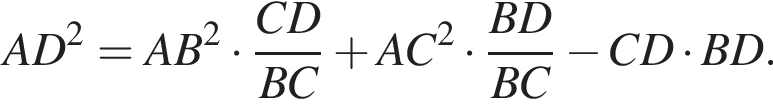

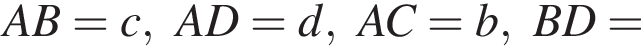

















 что и требовалось доказать.
что и требовалось доказать. (См. рис. 2).
(См. рис. 2).

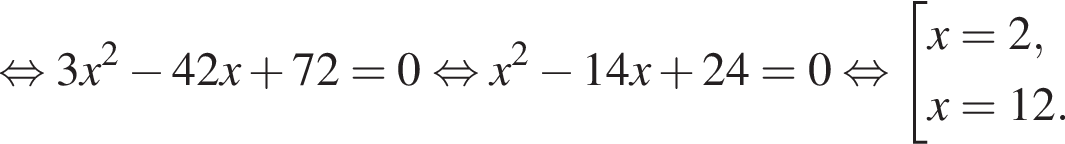






 то
то 



 (См. рис. 1) .
(См. рис. 1) . 











 в ΔABE
в ΔABE  Но
Но 


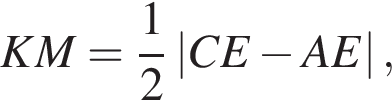 что и требовалось доказать.
что и требовалось доказать. 


 Значит,
Значит, 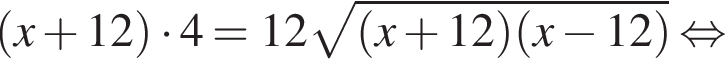



















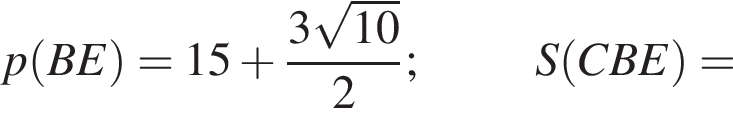










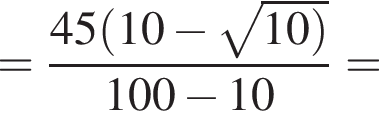






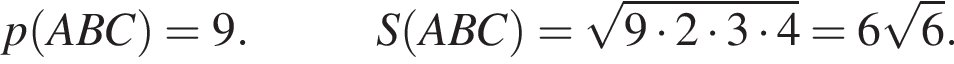



















 то
то  поэтому треугольники ABC и CBE подобны (по первому признаку подобия). Следовательно,
поэтому треугольники ABC и CBE подобны (по первому признаку подобия). Следовательно, 



 поскольку тогда
поскольку тогда  или
или  как перпендикуляры к одной прямой. Значит,
как перпендикуляры к одной прямой. Значит,  Обозначим основания высот треугольника ABC за
Обозначим основания высот треугольника ABC за 









 По теореме Менелая для треугольника
По теореме Менелая для треугольника 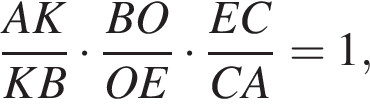
 Тогда
Тогда 
 По теореме Менелая для треугольника BAE и прямой KCO имеем
По теореме Менелая для треугольника BAE и прямой KCO имеем  откуда
откуда 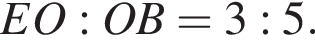 Тогда
Тогда 
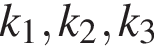 и заметим, что
и заметим, что  поскольку сумма сторон треугольников, параллельных данной стороне исходного треугольника, равна этой стороне (одна из трех там лежит, остальные две равны соответствующим частям стороны как противоположные стороны параллелограммов). Обозначая площади треугольников за
поскольку сумма сторон треугольников, параллельных данной стороне исходного треугольника, равна этой стороне (одна из трех там лежит, остальные две равны соответствующим частям стороны как противоположные стороны параллелограммов). Обозначая площади треугольников за  а площадь исходного за S, будем иметь
а площадь исходного за S, будем иметь

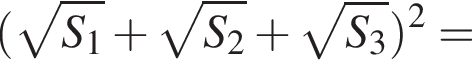



 откуда
откуда  и поэтому площадь последнего треугольника равна
и поэтому площадь последнего треугольника равна 
 Тогда четырехугольник AOBK — параллелограмм (его диагонали делятся пополам точкой пересечения))с прямым углом, поэтому его диагонали равны, то есть
Тогда четырехугольник AOBK — параллелограмм (его диагонали делятся пополам точкой пересечения))с прямым углом, поэтому его диагонали равны, то есть  что и требовалось.
что и требовалось.
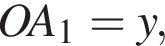

 По теореме пифагора имеем
По теореме пифагора имеем  откуда
откуда 
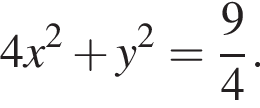 Решая эти уравнения, находим
Решая эти уравнения, находим 
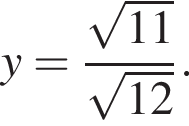


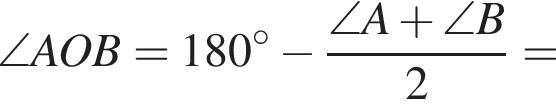

 и это угол между прямыми, поскольку он острый.
и это угол между прямыми, поскольку он острый.
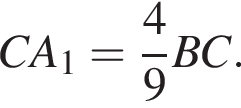




 откуда
откуда 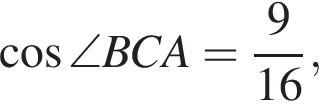



 Поэтому четырехугольник APKB вписанный и
Поэтому четырехугольник APKB вписанный и  поскольку они опираются на одну дугу.
поскольку они опираются на одну дугу. поэтому треугольники CPK и CBA подобны по двум углам, так как угол C общий. Вычислим коэффициент подобия.
поэтому треугольники CPK и CBA подобны по двум углам, так как угол C общий. Вычислим коэффициент подобия. поэтому
поэтому  Следовательно,
Следовательно,  по определению косинуса из треугольника AKC. Это и есть коэффициент подобия. Окончательно:
по определению косинуса из треугольника AKC. Это и есть коэффициент подобия. Окончательно: 
 то есть треугольник ACE равнобедренный. При этом его высота равна половине основания, поскольку
то есть треугольник ACE равнобедренный. При этом его высота равна половине основания, поскольку  Значит, она делит его на два равнобедренных прямоугольных треугольника,
Значит, она делит его на два равнобедренных прямоугольных треугольника,  то есть AC перпендикулярна CE. Тогда и AC перпендикулярна BD.
то есть AC перпендикулярна CE. Тогда и AC перпендикулярна BD. Значит, и их высоты отличаются в полтора раза, но разница между ними равна высоте трапеции, то есть
Значит, и их высоты отличаются в полтора раза, но разница между ними равна высоте трапеции, то есть  Значит, высота BTC равна
Значит, высота BTC равна  Получаем:
Получаем:
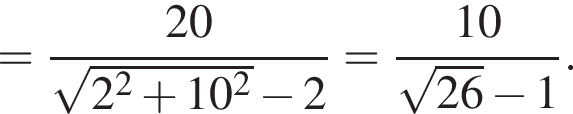









 Имеем:
Имеем:




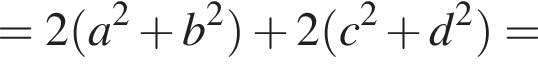

 поэтому
поэтому  и радиус окружности равен
и радиус окружности равен 


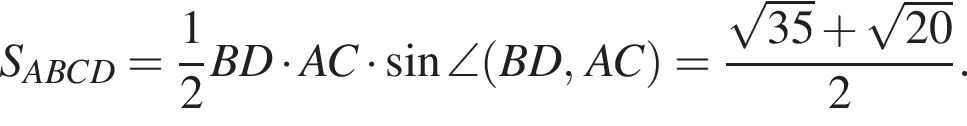





 — прямоугольная трапеция. Опустим из середины
— прямоугольная трапеция. Опустим из середины  тогда и для отрезка AB это будет серединный перпендикуляр.
тогда и для отрезка AB это будет серединный перпендикуляр. 

 (по два отрезка из точки T). Тогда:
(по два отрезка из точки T). Тогда: 










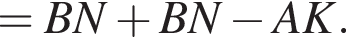
 откуда
откуда 
 находим
находим 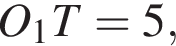
 Тогда, по теореме Пифагора,
Тогда, по теореме Пифагора, 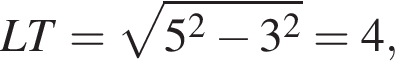 аналогично,
аналогично,  Тогда
Тогда  Но:
Но: 

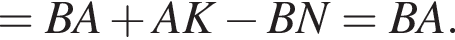



 поэтому
поэтому  Теперь можем найти AM:
Теперь можем найти AM:
 откуда
откуда 
 Пусть искомый отрезок имеет концы P, Q на AB, AC соответственно. Пусть
Пусть искомый отрезок имеет концы P, Q на AB, AC соответственно. Пусть  тогда
тогда 





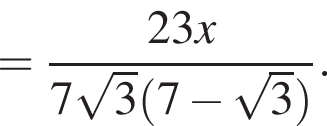



 лежат на одной окружности. Тогда
лежат на одной окружности. Тогда  — половине дуги
— половине дуги  что и требовалось доказать.
что и требовалось доказать. радиус маленькой —
радиус маленькой —  Но в такой окружности не может быть хорды
Но в такой окружности не может быть хорды  Тогда
Тогда 
 Тогда
Тогда 


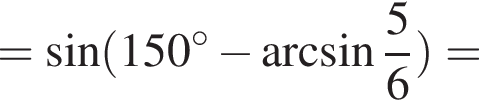





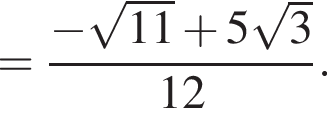
















 как опирающиеся на одну дугу. Тогда треугольники
как опирающиеся на одну дугу. Тогда треугольники 



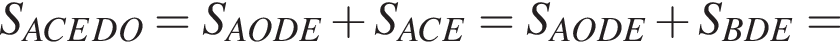



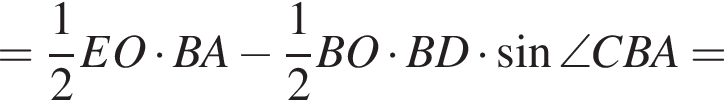



























 (они оба равны полусумме дуг CA и BE). Итак,
(они оба равны полусумме дуг CA и BE). Итак,  что и требовалось доказать.
что и требовалось доказать. Тогда треугольники
Тогда треугольники  Тогда треугольники
Тогда треугольники  так как оба угла равны
так как оба угла равны а
а  поскольку CD — биссектриса). Итак,
поскольку CD — биссектриса). Итак,  По теореме косинусов, обозначая
По теореме косинусов, обозначая  получим
получим


 (второй корень отрицательный).
(второй корень отрицательный). Тогда по теореме синусов для треугольника FDE:
Тогда по теореме синусов для треугольника FDE:

 поэтому
поэтому 





 поэтому в четырехугольнике
поэтому в четырехугольнике  и вписанная окружность действительно есть. Заметим, что KMDA — прямоугольник, поэтому точка
и вписанная окружность действительно есть. Заметим, что KMDA — прямоугольник, поэтому точка  Далее,
Далее, 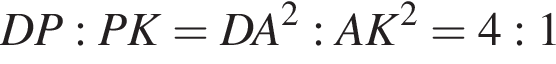 и при этом
и при этом 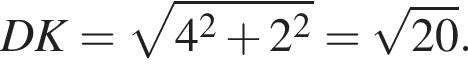




 Теперь найдем радиус по известной формуле
Теперь найдем радиус по известной формуле 
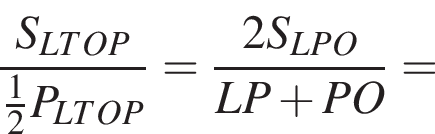


 откуда
откуда  Аналогично получим, что
Аналогично получим, что  Тогда KM параллельна AC, поскольку треугольники
Тогда KM параллельна AC, поскольку треугольники  Заметим, что
Заметим, что 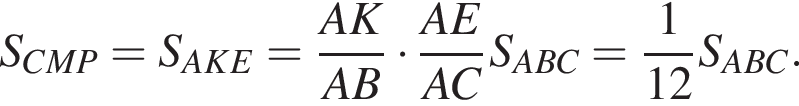


 На гипотенузе AB вне треугольника построен квадрат ABEF. Прямая CE пересекает AB в точке O.
На гипотенузе AB вне треугольника построен квадрат ABEF. Прямая CE пересекает AB в точке O.
 — на отношения отрезков или площадей это не влияет, мы просто сжимаем или растягиваем картинку. Тогда
— на отношения отрезков или площадей это не влияет, мы просто сжимаем или растягиваем картинку. Тогда 





 и по теореме косинусов
и по теореме косинусов 
 По теореме синусов в треугольнике
По теореме синусов в треугольнике 
 Значит,
Значит, 



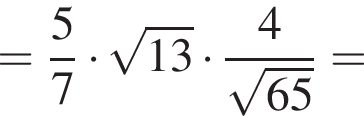
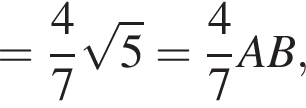
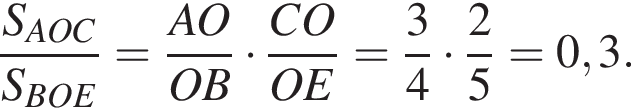

 поэтому
поэтому  По теореме синусов имеем также
По теореме синусов имеем также  поэтому
поэтому  Пусть K — точка пересечения
Пусть K — точка пересечения 







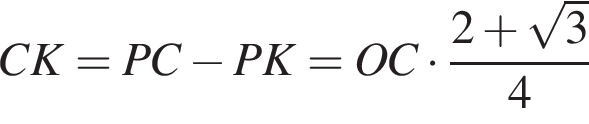 и
и 


 поэтому
поэтому  — параллелограмм и середины отрезков
— параллелограмм и середины отрезков 
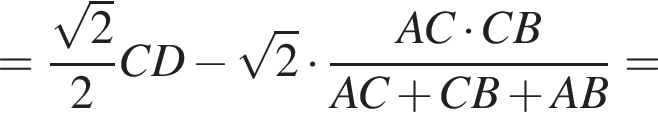

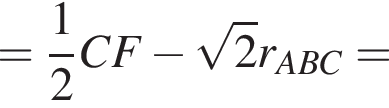



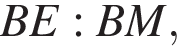 если
если 










 Пусть
Пусть  тогда по пункту а)
тогда по пункту а)  По теореме Пифагора
По теореме Пифагора

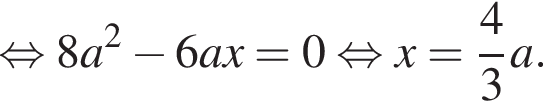

 Четырёхугольник KDEB — параллелограмм, поскольку его диагонали делятся точкой пересечения пополам, значит,
Четырёхугольник KDEB — параллелограмм, поскольку его диагонали делятся точкой пересечения пополам, значит,  Тогда
Тогда 


 тогда
тогда  а вневписанной
а вневписанной  Тогда:
Тогда: 



 и
и 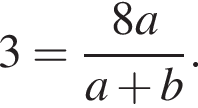

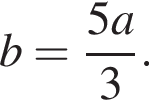 Подставляя в первое, получаем:
Подставляя в первое, получаем: 
 Тогда:
Тогда: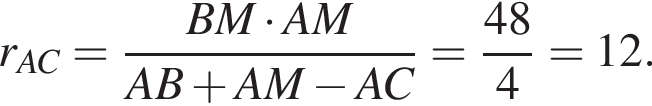









 В треугольнике отрезок от вершины до точки касания с вписанной окружностью можно вычислить по формуле
В треугольнике отрезок от вершины до точки касания с вписанной окружностью можно вычислить по формуле 



 Прямые
Прямые  если площадь треугольника
если площадь треугольника 
 Отсюда и следует нужное утверждение, поскольку высоты у данных треугольников совпадают.
Отсюда и следует нужное утверждение, поскольку высоты у данных треугольников совпадают.
 Тогда:
Тогда: 





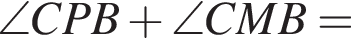




 Тогда в равнобедренном треугольнике AMC находим:
Тогда в равнобедренном треугольнике AMC находим: 

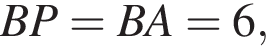




 Первая окружность вписана в треугольник АВС, а вторая касается AB и продолжения сторон BC и AC.
Первая окружность вписана в треугольник АВС, а вторая касается AB и продолжения сторон BC и AC.

 По обратной теореме Пифагора он прямоугольный, поэтому его площадь
По обратной теореме Пифагора он прямоугольный, поэтому его площадь  полупериметр
полупериметр 
 что и требовалось доказать.
что и требовалось доказать.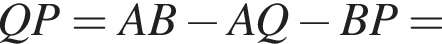










 и
и  равны
равны 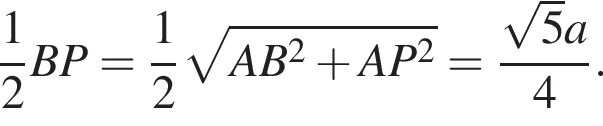
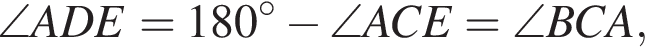
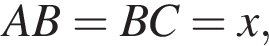 тогда:
тогда: 






 ). Тогда по свойству вписанного четырехугольника (AQPC) имеем:
). Тогда по свойству вписанного четырехугольника (AQPC) имеем:
 поэтому они подобны с коэффициентом
поэтому они подобны с коэффициентом  в частности
в частности  Пусть
Пусть 
 Тогда:
Тогда: 
 Далее:
Далее:  аналогично
аналогично  Теперь напишем теорему Пифагора для треугольников APC и
Теперь напишем теорему Пифагора для треугольников APC и 


 получим
получим  откуда
откуда  Тогда:
Тогда: 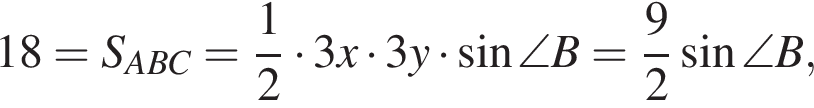


 и
и 

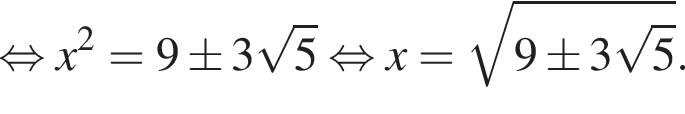




 то треугольник ABC получится тупоугольным, поскольку
то треугольник ABC получится тупоугольным, поскольку 
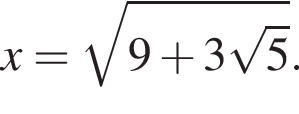 Но тогда площадь ABC равна:
Но тогда площадь ABC равна: 



 в этой системе не учитывалось никак, например.
в этой системе не учитывалось никак, например.
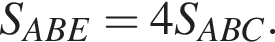 Заметим, что треугольники ABC и EBA подобны по двум углам:
Заметим, что треугольники ABC и EBA подобны по двум углам:  (первый — угол между касательной и хордой к большой окружности, второй — вписанный угол в ней же, оба равны половине дуги AB) и аналогично
(первый — угол между касательной и хордой к большой окружности, второй — вписанный угол в ней же, оба равны половине дуги AB) и аналогично  Коэффициент подобия равен
Коэффициент подобия равен 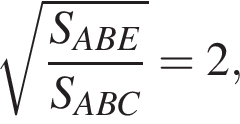 поэтому
поэтому 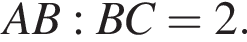
 По свойству биссектрисы тогда
По свойству биссектрисы тогда 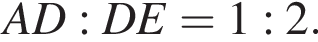 Имеем:
Имеем:


 и площадь четырехугольника BTMR равна 24.
и площадь четырехугольника BTMR равна 24.
 Значит,
Значит,  а треугольник MKL подобен треугольнику MRT с коэффициентом
а треугольник MKL подобен треугольнику MRT с коэффициентом  поэтому его площадь в
поэтому его площадь в  раз больше. Наконец, у треугольника ABC высота та же, а основание в
раз больше. Наконец, у треугольника ABC высота та же, а основание в 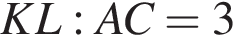 раза меньше, поэтому его площадь равна
раза меньше, поэтому его площадь равна 
 откуда
откуда  В решении мы нигде не использовали то, что AB диаметр, наше доказательство годится во всех случаях.
В решении мы нигде не использовали то, что AB диаметр, наше доказательство годится во всех случаях.









 поэтому абсциссы точек A и B находятся так —
поэтому абсциссы точек A и B находятся так —  Пусть
Пусть 
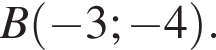 Пусть, далее, точка C имеет координаты
Пусть, далее, точка C имеет координаты  а во-вторых:
а во-вторых: 

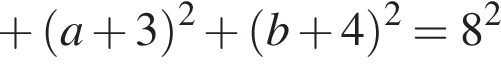


 Значит, точка C лежит левее AB, а центр окружностей правее.
Значит, точка C лежит левее AB, а центр окружностей правее. поэтому площадь треугольника равна
поэтому площадь треугольника равна 



 (если они перекрываются, то под модулем будет
(если они перекрываются, то под модулем будет 



 тогда из первого пункта
тогда из первого пункта  По формулам для радиусов вписанной и вневписанной окружности имеем:
По формулам для радиусов вписанной и вневписанной окружности имеем: 





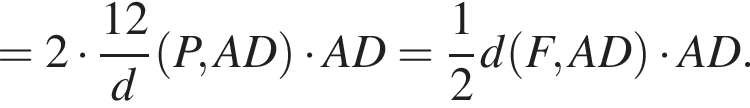


















 и двум углам (
и двум углам (
 как накрест лежащие при параллельных AD и FE). Значит,
как накрест лежащие при параллельных AD и FE). Значит,  По теореме Менелая для треугольника EAF и прямой OPT имеем:
По теореме Менелая для треугольника EAF и прямой OPT имеем:
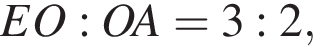 поэтому:
поэтому: 


 Треугольники
Треугольники 
 как угол между касательной и радиусом. Значит,
как угол между касательной и радиусом. Значит, 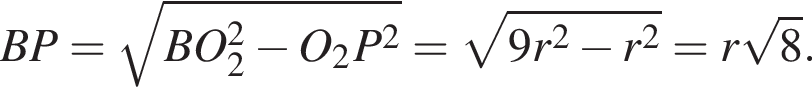


 потому что опирается на диаметр большой окружности) с коэффициентом
потому что опирается на диаметр большой окружности) с коэффициентом  поэтому
поэтому  Итак,
Итак, 








 и
и  а тогда и
а тогда и  Значит, у треугольников ABC и ADC с общим основанием AC одинаковые высоты. Тогда их площади равны.
Значит, у треугольников ABC и ADC с общим основанием AC одинаковые высоты. Тогда их площади равны.


 и
и  Тогда:
Тогда: 

 Пусть O — центр окружности. Тогда CO и DO — биссектрисы соответствующих углов и
Пусть O — центр окружности. Тогда CO и DO — биссектрисы соответствующих углов и 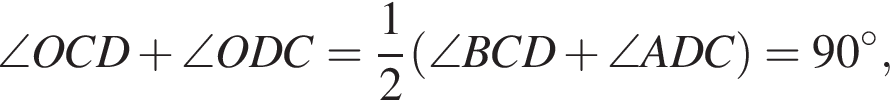


 По теореме Пифагора в треугольнике COD имеем
По теореме Пифагора в треугольнике COD имеем



 Отрезки касательных, проведенных из одной точки, равны, поэтому:
Отрезки касательных, проведенных из одной точки, равны, поэтому: 

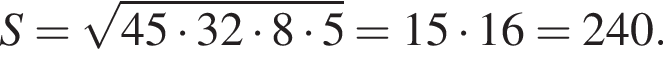
 и площадь трапеции составляет
и площадь трапеции составляет 































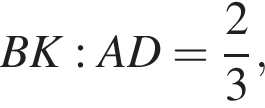 поэтому
поэтому
 откуда и следует утверждение п. а).
откуда и следует утверждение п. а). (поскольку KP : PD = 1 : 3 по соображениям, аналогичным п. а)) и расстояние составит
(поскольку KP : PD = 1 : 3 по соображениям, аналогичным п. а)) и расстояние составит

 что и требовалось доказать.
что и требовалось доказать. при этом дуга CE равна четверти окружности. Значит, хорда длины
при этом дуга CE равна четверти окружности. Значит, хорда длины 
 и площадь треугольника равна
и площадь треугольника равна 
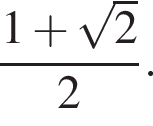

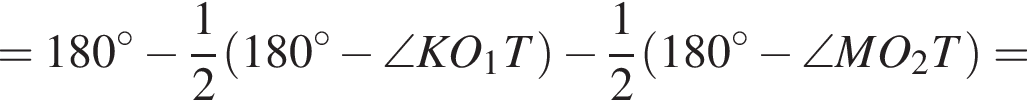
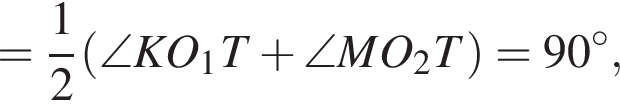

 По формуле для радиуса вписанной окружности имеем
По формуле для радиуса вписанной окружности имеем 
 откуда
откуда 
 откуда
откуда 
 подобны. Обозначив
подобны. Обозначив  найдем
найдем откуда
откуда  Значит,
Значит,  и
и  Тогда по теореме косинусов имеем
Тогда по теореме косинусов имеем 
 Получим
Получим и
и 
 Подставим это в предыдущее и получим
Подставим это в предыдущее и получим  откуда
откуда  Значит,
Значит,  и мы можем по теореме Виета угадать стороны
и мы можем по теореме Виета угадать стороны  (первые две можно было бы поменять местами, но по условию AC — наибольшаяя сторона).
(первые две можно было бы поменять местами, но по условию AC — наибольшаяя сторона). то есть
то есть  и
и 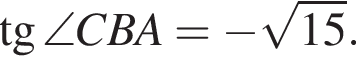

 Опустим перпендикуляр KH на AC и отметим на AC точку
Опустим перпендикуляр KH на AC и отметим на AC точку  Тогда в треугольнике CKE высота совпадает с медианой и
Тогда в треугольнике CKE высота совпадает с медианой и  Значит, у треугольников
Значит, у треугольников 
 поэтому построенная таким образом точка совпадает с точкой E, перпендикуляр- с перпендикуляром из задачи и точка
поэтому построенная таким образом точка совпадает с точкой E, перпендикуляр- с перпендикуляром из задачи и точка 
 откуда
откуда  По формуле для биссектрисы имеем
По формуле для биссектрисы имеем 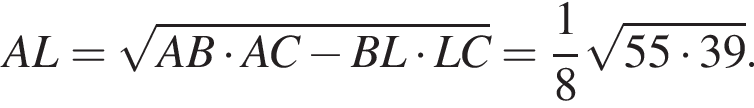 По теореме о пересекающихся хордах
По теореме о пересекающихся хордах 

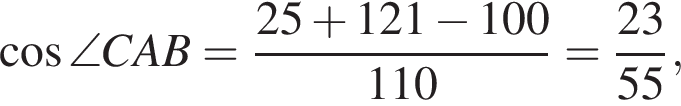 Значит,
Значит,  откуда
откуда 

 Отрезки АЕ и CD пересекаются в точке О.
Отрезки АЕ и CD пересекаются в точке О. 
 откуда
откуда 
 откуда
откуда  и
и  Кроме того
Кроме того 

 тогда
тогда  Снова применим теорему косинусов к этому треугольнику, получим
Снова применим теорему косинусов к этому треугольнику, получим  откуда
откуда  Наконец, по теореме косинусов для треугольника AOD находим
Наконец, по теореме косинусов для треугольника AOD находим  откуда
откуда 
 По теореме Фалеса
По теореме Фалеса  и Значит,
и Значит,  По свойству биссектрисы
По свойству биссектрисы  откуда
откуда  что и требовалось.
что и требовалось.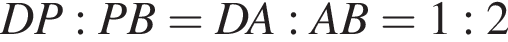 по свойству биссектрисы. Значит,
по свойству биссектрисы. Значит,
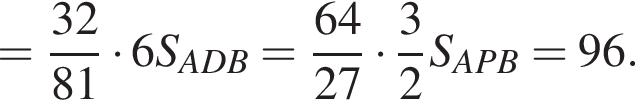



 По свойству биссектрисы
По свойству биссектрисы  поэтому
поэтому  По свойству пересекающихся хорд
По свойству пересекающихся хорд  откуда
откуда  Значит,
Значит,  (опираются на дугу BE описанной окружности), откуда
(опираются на дугу BE описанной окружности), откуда 
 откуда
откуда 
 тогда
тогда 

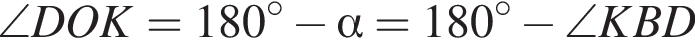 откуда четырехугольник DOKB — вписанный.
откуда четырехугольник DOKB — вписанный. поэтому треугольник — прямоугольный, поэтому
поэтому треугольник — прямоугольный, поэтому  и
и  длина же самого серединного перпендикуляра равна
длина же самого серединного перпендикуляра равна 







 поскольку эти углы опираются на диаметр.
поскольку эти углы опираются на диаметр. откуда по теореме косинусов
откуда по теореме косинусов 

 поэтому
поэтому  и
и  откуда
откуда 
 откуда
откуда  поэтому
поэтому  В прямоугольном треугольнике CHB имеем
В прямоугольном треугольнике CHB имеем  откуда
откуда  и
и 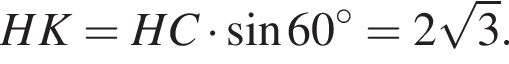
 как опирающиеся на ону дугу KP в окружности. Значит,
как опирающиеся на ону дугу KP в окружности. Значит,  Тогда по теореме косинусов
Тогда по теореме косинусов





 Тогда
Тогда  и
и  поэтому MBPK — вписанный четырехугольник. Заметим далее, что поскольку
поэтому MBPK — вписанный четырехугольник. Заметим далее, что поскольку  то прямая KC составляет с BK ровно такой же угол, как касательная в точке
то прямая KC составляет с BK ровно такой же угол, как касательная в точке 



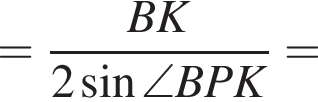


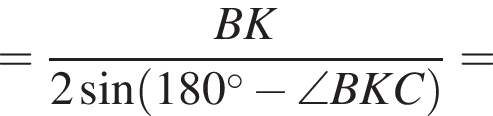




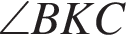 из треугольника BKC по теореме косинусов. Заметим, что
из треугольника BKC по теореме косинусов. Заметим, что









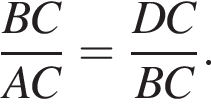 Тогда треугольники BCA и DCB подобны по углу C и отношению сторон. Значит,
Тогда треугольники BCA и DCB подобны по углу C и отношению сторон. Значит, 
 находим
находим 










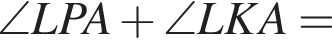





 откуда
откуда 
 Поскольку
Поскольку  и
и  (последнее равенство верно, поскольку
(последнее равенство верно, поскольку  ), треугольники BCL, PCL, ACK подобны (первые два даже равны, потому что у них общая сторона CL). Тогда:
), треугольники BCL, PCL, ACK подобны (первые два даже равны, потому что у них общая сторона CL). Тогда:









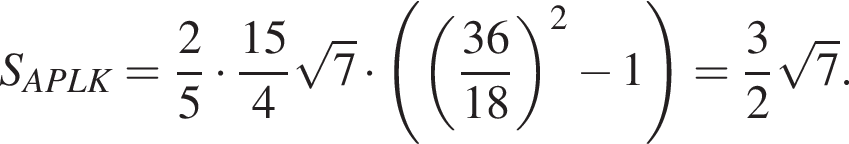





 тогда
тогда  где O — точка пересечения диагоналей параллелограмма. Далее,
где O — точка пересечения диагоналей параллелограмма. Далее,  откуда
откуда  В треугольнике KLM отрезок LO — медиана, значит, P — точка пересечения медиан. Итак, KP — медиана, поэтому R — середина LM. Аналогично для треугольника KMN получаем, что S — середина MN.
В треугольнике KLM отрезок LO — медиана, значит, P — точка пересечения медиан. Итак, KP — медиана, поэтому R — середина LM. Аналогично для треугольника KMN получаем, что S — середина MN.




 (вертикальные углы, опирающиеся на одну дугу, соответственные), поэтому треугольники подобны по двум углам, угол K у них общий.
(вертикальные углы, опирающиеся на одну дугу, соответственные), поэтому треугольники подобны по двум углам, угол K у них общий. тогда
тогда 
 поскольку медианы делятся точкой пересечения в отношении
поскольку медианы делятся точкой пересечения в отношении  то есть
то есть  откуда
откуда  и
и 



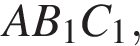 если известно, что
если известно, что 

 и
и 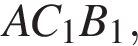 то есть его центр вписанной окружности. Поэтому нужно найти
то есть его центр вписанной окружности. Поэтому нужно найти  Вычислим:
Вычислим: 




 Отрезки СЕ и AD пересекаются в точке О.
Отрезки СЕ и AD пересекаются в точке О.
 Значит, треугольник AEC равнобедренный, поэтому его биссектриса совпадает с медианой. Итак,
Значит, треугольник AEC равнобедренный, поэтому его биссектриса совпадает с медианой. Итак,  что и требовалось доказать.
что и требовалось доказать. тогда
тогда  и
и 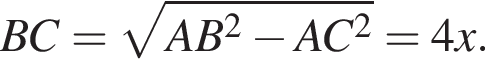 Поскольку AD — биссектриса,
Поскольку AD — биссектриса, 
 Тогда:
Тогда: 





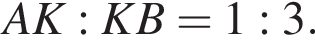

 Значит,
Значит, 
 По свойству биссектрисы тогда
По свойству биссектрисы тогда  и
и  по свойству треугольников с общей высотой.
по свойству треугольников с общей высотой. поэтому
поэтому  Следовательно,
Следовательно,  поскольку AO — биссектриса треугольника BAE.
поскольку AO — биссектриса треугольника BAE.

 откуда
откуда 
 Значит,
Значит,  и
и  откуда:
откуда: 







 проведена медиана AD и биссектриса СЕ, пересекающиеся в точке M. Через M проведена прямая, параллельная AC и пересекающая стороны AB и BC в точках P и Q соответственно.
проведена медиана AD и биссектриса СЕ, пересекающиеся в точке M. Через M проведена прямая, параллельная AC и пересекающая стороны AB и BC в точках P и Q соответственно.
 По свойству биссектрисы в треугольнике ACD имеем
По свойству биссектрисы в треугольнике ACD имеем 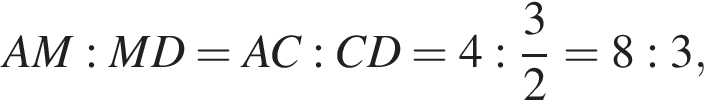
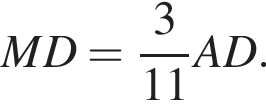 Из подобия треугольников DMQ и DAC получаем:
Из подобия треугольников DMQ и DAC получаем: 

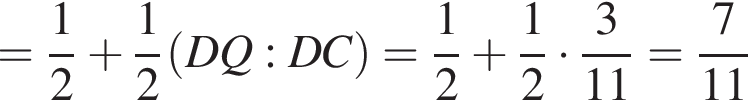






 поэтому
поэтому  Значит, у подобного ему PQB радиус равен
Значит, у подобного ему PQB радиус равен 
 Точка D' симметрична точке D относительно прямой BC, точка D'' симметрична точке D’ относительно прямой AC и лежит на прямой BC. Известно, что
Точка D' симметрична точке D относительно прямой BC, точка D'' симметрична точке D’ относительно прямой AC и лежит на прямой BC. Известно, что 


 Тогда
Тогда 
 и
и  откуда
откуда  Кроме того,
Кроме того, 

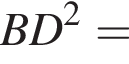

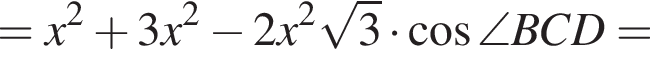















 Кроме того, BC — диаметр окружности, а M — ее центр. Пусть O — точка пересечения медиан треугольника ABC. Обозначим
Кроме того, BC — диаметр окружности, а M — ее центр. Пусть O — точка пересечения медиан треугольника ABC. Обозначим 
 Тогда
Тогда 



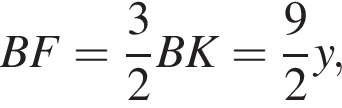
 Применим теорему о равенстве произведений отрезков хорд:
Применим теорему о равенстве произведений отрезков хорд:
 Далее:
Далее:

 Значит,
Значит, 
 тогда
тогда 


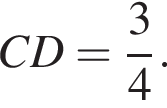
 (треугольник EDA по условию равнобедренный), тогда и
(треугольник EDA по условию равнобедренный), тогда и  (поскольку DE и AD — биссектрисы). Тогда
(поскольку DE и AD — биссектрисы). Тогда  и
и  Значит, треугольники AED и ADC подобны по двум углам, то есть
Значит, треугольники AED и ADC подобны по двум углам, то есть  и
и  откуда
откуда 

 Далее,
Далее,  поэтому прямая ED параллельна прямой AC и треугольники BED и BAC подобны с коэффициентом
поэтому прямая ED параллельна прямой AC и треугольники BED и BAC подобны с коэффициентом  Значит,
Значит,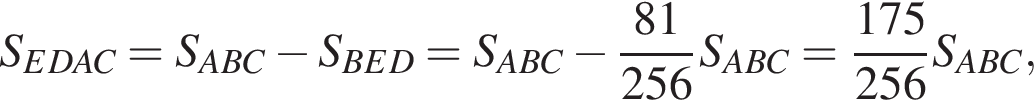





 по теореме о вписанном угле. Треугольник OBC прямоугольный, поскольку касательная перепендикулярна радиусу, проведенному в точку касания. То есть
по теореме о вписанном угле. Треугольник OBC прямоугольный, поскольку касательная перепендикулярна радиусу, проведенному в точку касания. То есть 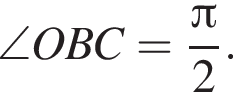 Тогда третий угол треугольника OBC равен
Тогда третий угол треугольника OBC равен 
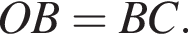

 поэтому
поэтому  Кроме того,
Кроме того,  По теореме синусов тогда
По теореме синусов тогда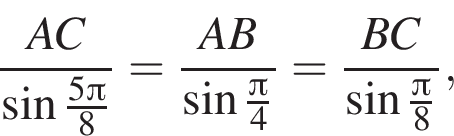
 и
и 





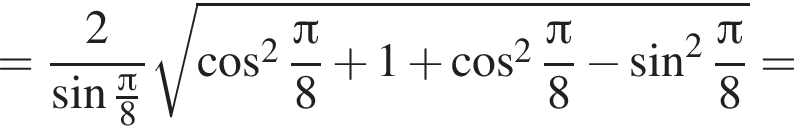







 (из того, что
(из того, что  ).
). откуда
откуда 

 а из подобия треугольников CKM и CBH следует, что
а из подобия треугольников CKM и CBH следует, что 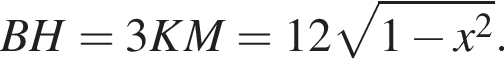






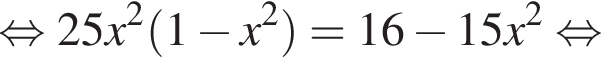
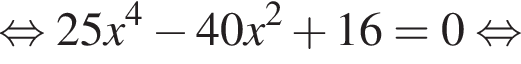




 и
и 


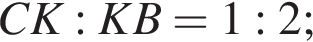 б)
б) 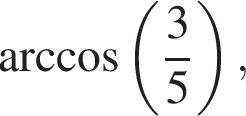 вписан в окружность радиуса
вписан в окружность радиуса  Тогда
Тогда 
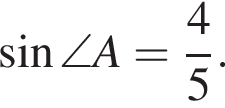 Поскольку четырехугольник вписанный,
Поскольку четырехугольник вписанный,  Значит,
Значит, 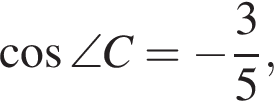
 Пусть, далее,
Пусть, далее, 

 тогда, из-за описанности,
тогда, из-за описанности, 

 откуда
откуда  Найдем двумя способами площадь четырехугольника ABCD. Во-первых, она равна
Найдем двумя способами площадь четырехугольника ABCD. Во-первых, она равна 







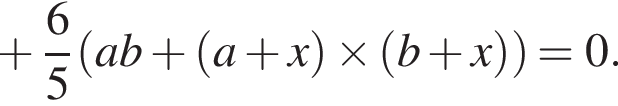



 поскольку это полупериметр. Значит,
поскольку это полупериметр. Значит,  Теперь сделаем замену
Теперь сделаем замену 
 и запишем первые два уравнения.
и запишем первые два уравнения.










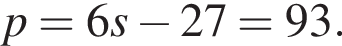 Тогда a, b — корни квадратного уравнения
Тогда a, b — корни квадратного уравнения  то есть они равны
то есть они равны 



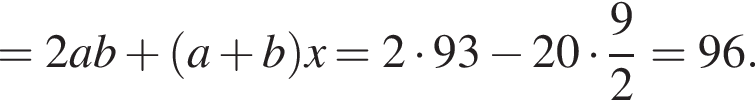







 медиана
медиана  На биссектрисе СЕ выбрана точка F такая, что
На биссектрисе СЕ выбрана точка F такая, что  Через точку F проведена прямая l, параллельная BC.
Через точку F проведена прямая l, параллельная BC.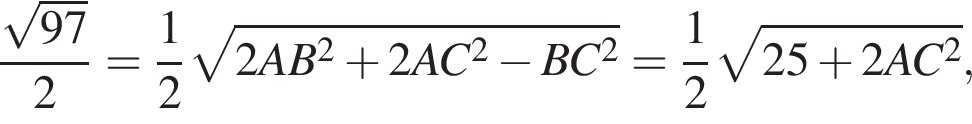
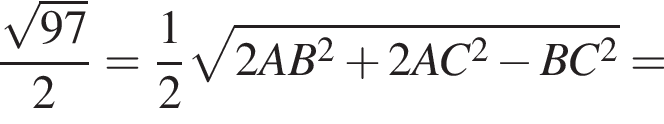
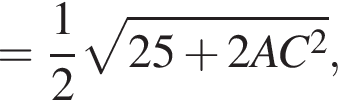

 Обозначим за T точку пересечения прямой l с AB.
Обозначим за T точку пересечения прямой l с AB.
 Поскольку прямая l параллельна прямой BC, треугольники BEC и TEF подобны с коэффициентом
Поскольку прямая l параллельна прямой BC, треугольники BEC и TEF подобны с коэффициентом 

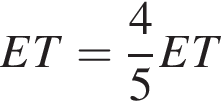 и
и  Поэтому расстояние между l и AB равно
Поэтому расстояние между l и AB равно 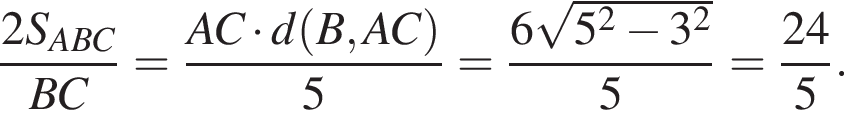



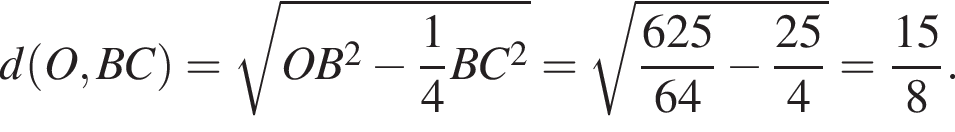


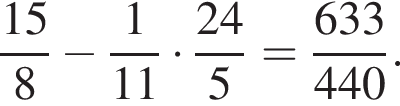






 По теореме Пифагора для треугольника ALE имеем
По теореме Пифагора для треугольника ALE имеем 
 По теореме Пифагора для треугольника BLE получим
По теореме Пифагора для треугольника BLE получим  Значит, и
Значит, и  Тогда по теореме Пифагора для треугольника ACE получим:
Тогда по теореме Пифагора для треугольника ACE получим: 


 Значит,
Значит, 




 и
и 
 б)
б)  и
и 

 поскольку опирается на диаметр окружности, поэтому P — основание высоты из вершины прямого угла. QPLM — вписанная в данную окружность трапеция, поэтому она равнобедренная и
поскольку опирается на диаметр окружности, поэтому P — основание высоты из вершины прямого угла. QPLM — вписанная в данную окружность трапеция, поэтому она равнобедренная и 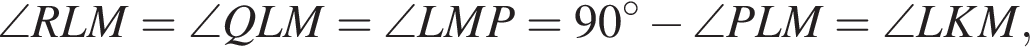




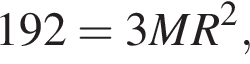









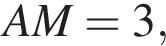


 и BNC опираются на диаметр, они прямые. То есть CM и BN — высоты треугольника (и Значит, он остроугольный, иначе хоть одна из точек M и N лежала бы на продолжении стороны), а P — его точка пересечения высот. Тогда
и BNC опираются на диаметр, они прямые. То есть CM и BN — высоты треугольника (и Значит, он остроугольный, иначе хоть одна из точек M и N лежала бы на продолжении стороны), а P — его точка пересечения высот. Тогда  как медианы прямоугольных треугольников ANP и AMP, равные половине общей гипотенузы.
как медианы прямоугольных треугольников ANP и AMP, равные половине общей гипотенузы. откуда
откуда  и
и  По теореме Пифагора для треугольника BNA получим
По теореме Пифагора для треугольника BNA получим 








 откуда
откуда 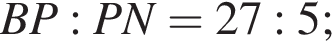








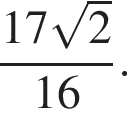
 хорда KN окружности, описанной около треугольника ABC, пересекает отрезки AC и BC в точках M и L соответственно. Известно, что
хорда KN окружности, описанной около треугольника ABC, пересекает отрезки AC и BC в точках M и L соответственно. Известно, что  площадь четырехугольника ABLM равна 2, а длина LM равна 1.
площадь четырехугольника ABLM равна 2, а длина LM равна 1. поэтому
поэтому 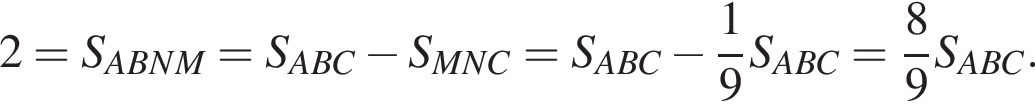

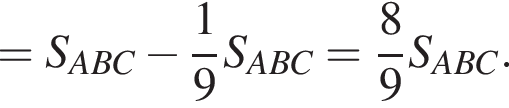
 Обозначим стороны треугольника
Обозначим стороны треугольника 
 Тогда
Тогда 
 По теореме косинусов для треугольника ABC в то же время имеем
По теореме косинусов для треугольника ABC в то же время имеем 


 поэтому
поэтому  и
и  Значит, a и b являются корнями квадратного уравнения
Значит, a и b являются корнями квадратного уравнения 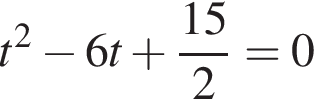 (теорема Виета), поэтому они равны
(теорема Виета), поэтому они равны  Будем считать, что
Будем считать, что  тогда
тогда 


 Из подобия, кроме того,
Из подобия, кроме того, 
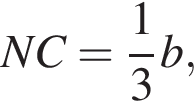

 По свойству пересекающихся хорд имеем
По свойству пересекающихся хорд имеем  и
и  Далее:
Далее: и
и 






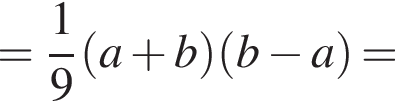
 Прибавляя к этому уравнению удвоенное уравнение
Прибавляя к этому уравнению удвоенное уравнение  получим:
получим:





 Продолжение биссектрисы AF угла A этого треугольника пересекает окружность в точке L, а радиус AO пересекает сторону BC в точке E. Пусть AH — высота треугольника ABC. Известно, что
Продолжение биссектрисы AF угла A этого треугольника пересекает окружность в точке L, а радиус AO пересекает сторону BC в точке E. Пусть AH — высота треугольника ABC. Известно, что 


 Тогда
Тогда 









 Треугольник AOL — равнобедренный, поэтому
Треугольник AOL — равнобедренный, поэтому  По теореме синусов для треугольника AOL получаем
По теореме синусов для треугольника AOL получаем  откуда
откуда  Площадь AOL равна
Площадь AOL равна 















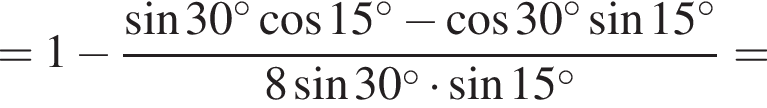


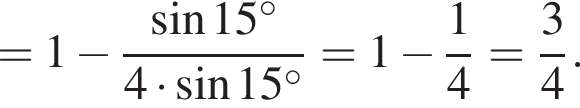


 то коэффициент подобия CEB и DEA равен трем,
то коэффициент подобия CEB и DEA равен трем, 

 и
и 




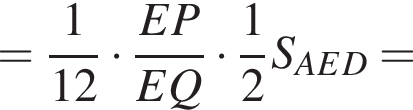



 Обозначим
Обозначим 

 тогда
тогда 
 поэтому
поэтому  Далее,
Далее,  поскольку первый из них — вписанный, опирающийся на дугу AB, а второй — угол между касательной и хордой, стягивающей дугу AB. Значит, и
поскольку первый из них — вписанный, опирающийся на дугу AB, а второй — угол между касательной и хордой, стягивающей дугу AB. Значит, и  откуда прямая AT параллельна прямой LM и треугольники AKT и LKM подобны, поэтому
откуда прямая AT параллельна прямой LM и треугольники AKT и LKM подобны, поэтому 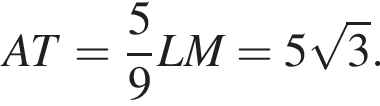
 откуда
откуда 
 или
или  тогда
тогда  и
и  По свойству биссектрисы
По свойству биссектрисы  откуда
откуда  Тогда по условию
Тогда по условию 




 (верное при любых значениях переменных) не выполняется в этом случае. Значит,
(верное при любых значениях переменных) не выполняется в этом случае. Значит,  и
и  Тогда
Тогда 







 как вписанные углы, опирающиеся на одну дугу описанной окружности AMNC.
как вписанные углы, опирающиеся на одну дугу описанной окружности AMNC.







 откуда
откуда  и ответ
и ответ 


 получаем:
получаем: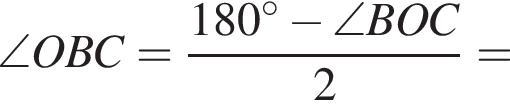
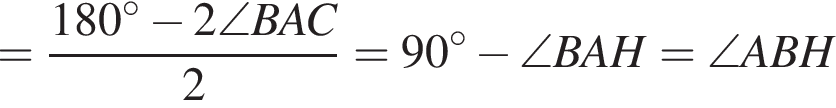


 Тогда из прямоугольных треугольников ABH и OBT получаем:
Тогда из прямоугольных треугольников ABH и OBT получаем: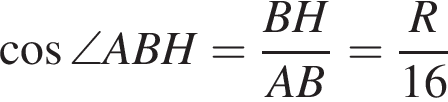 и
и 
 откуда
откуда  и
и 


 как отрезки касательных, проведенных из одной точки. Тогда в прямоугольном треугольнике COP имеем
как отрезки касательных, проведенных из одной точки. Тогда в прямоугольном треугольнике COP имеем 
 откуда
откуда  и
и 



 Кроме того, уравнение прямой CP это
Кроме того, уравнение прямой CP это  то есть
то есть  Значит, координаты точки P имеют вид
Значит, координаты точки P имеют вид  при этом
при этом  Значит,
Значит,  откуда
откуда  (
( Найдем уравнение прямой AM. Оно имеет вид
Найдем уравнение прямой AM. Оно имеет вид 


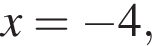

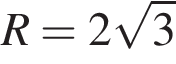 от точки O. Пусть ее координата по y равна t, тогда координата по x равна
от точки O. Пусть ее координата по y равна t, тогда координата по x равна  и расстояние до O получается:
и расстояние до O получается:


 Значит,
Значит,  Тогда
Тогда 
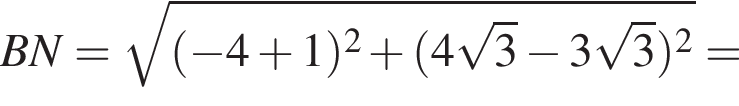


 и вычислим расстояние от K до этой прямой: ##
и вычислим расстояние от K до этой прямой: ##


 поэтому
поэтому  Обозначим этот угол
Обозначим этот угол  а
а 
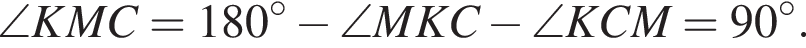






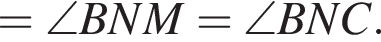
 треугольник BMN равнобедренный и
треугольник BMN равнобедренный и  Значит, BNAC — параллелограмм (его диагонали делятся пополам точкой пересечения), поэтому
Значит, BNAC — параллелограмм (его диагонали делятся пополам точкой пересечения), поэтому 






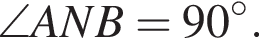

 Проведём прямую MN параллельно AD. Пусть h1 — высота треугольника CMN, проведённая к MN, h2 — высота треугольника DMN, проведённая к MN, h — высота ABCD. Следовательно,
Проведём прямую MN параллельно AD. Пусть h1 — высота треугольника CMN, проведённая к MN, h2 — высота треугольника DMN, проведённая к MN, h — высота ABCD. Следовательно, 

 Следовательно,
Следовательно, 













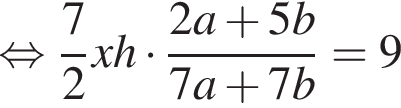


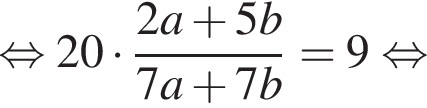




 Положим
Положим  тогда
тогда 


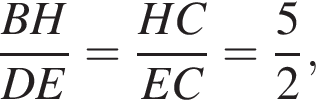 откуда
откуда  что и требовалось доказать.
что и требовалось доказать.
 откуда
откуда 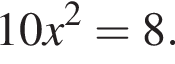 Тогда:
Тогда:


 откуда
откуда  Треугольники BMD и BHC подобны, следовательно,
Треугольники BMD и BHC подобны, следовательно, 

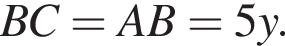 Треугольник ABD — прямоугольный, тогда
Треугольник ABD — прямоугольный, тогда





 значит, и отношение радиусов равно 5 : 13.
значит, и отношение радиусов равно 5 : 13.



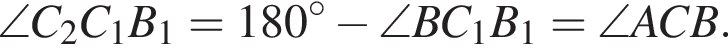



 откуда
откуда 





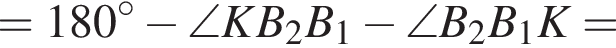
 Таким образом,
Таким образом, 
 Проведем TN параллельно ВР. Заметим, что
Проведем TN параллельно ВР. Заметим, что  поскольку NT — средняя линия треугольника APQ. Значит, площади треугольников ASB и AST равны, так как в них BS = ST, а высота, проведенная из вершины A, — общая.
поскольку NT — средняя линия треугольника APQ. Значит, площади треугольников ASB и AST равны, так как в них BS = ST, а высота, проведенная из вершины A, — общая. откуда
откуда  Из пункта а) известно, что треугольники NTS и PBS равны,
Из пункта а) известно, что треугольники NTS и PBS равны,  и
и  Значит,
Значит,  а тогда:
а тогда:
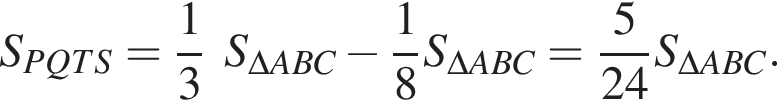
 поэтому KCMB вписан в окружность с диаметром BC, отсюда углы CMK и CBK равны 30°. Аналогично углы CML и CDL равны 30°, откуда угол KML равен 60°. Кроме того, треугольники KBM и LDM равны по двум сторонам и углу между ними. Таким образом, стороны LM и MK равны, следовательно, треугольник LMK равносторонний.
поэтому KCMB вписан в окружность с диаметром BC, отсюда углы CMK и CBK равны 30°. Аналогично углы CML и CDL равны 30°, откуда угол KML равен 60°. Кроме того, треугольники KBM и LDM равны по двум сторонам и углу между ними. Таким образом, стороны LM и MK равны, следовательно, треугольник LMK равносторонний. отсюда
отсюда  Пусть
Пусть  по теореме синусов
по теореме синусов




 откуда
откуда  следовательно,
следовательно, 



 Тогда
Тогда  а
а  по свойству медианы. Следовательно,
по свойству медианы. Следовательно, 

 тогда
тогда 
 Значит,
Значит, 
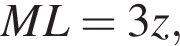 тогда
тогда 
 следовательно,
следовательно, 


 (треугольники имеют общую высоту, проведенную из вершины A, BK = KC), аналогично
(треугольники имеют общую высоту, проведенную из вершины A, BK = KC), аналогично  значит,
значит, 


 значит,
значит, 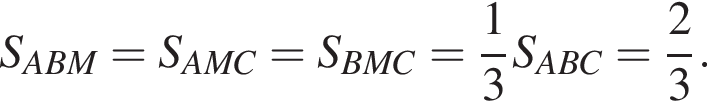

 Аналогично, треугольники BMR и BMC имеют общую высоту, проведенную из вершины B, значит,
Аналогично, треугольники BMR и BMC имеют общую высоту, проведенную из вершины B, значит, 
 Следовательно,
Следовательно, 
 (треугольники PMB и PMQ имеют общую высоту из вершины P, их площади относятся как основания BM и QM),
(треугольники PMB и PMQ имеют общую высоту из вершины P, их площади относятся как основания BM и QM), 
 Площадь
Площадь  (треугольники имеют общую высоту, проведенную из вершины R, их площади относятся как основания PM и AR). Имеем:
(треугольники имеют общую высоту, проведенную из вершины R, их площади относятся как основания PM и AR). Имеем:
 Получаем:
Получаем:


 Из подобия треугольников получаем
Из подобия треугольников получаем 
 Выразим площадь треугольника KMP:
Выразим площадь треугольника KMP: