1. Тип Д17 C6 № 505590 

Классификатор алгебры: Неравенства с параметром
Сложные задачи с параметром. Неравенства с параметром
i
Найти все значения параметра a, при каждом из которых неравенство выполняется для всех x.
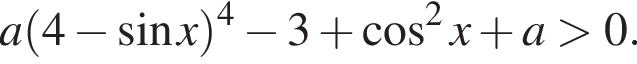
Решение. Преобразуем неравенство:


Таким образом, просто нужно чтобы a было больше наибольшего значения функции  Оно, очевидно, достигается при
Оно, очевидно, достигается при  то есть при
то есть при  поскольку
поскольку 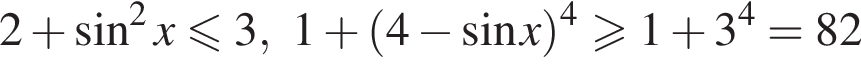 и оба равенства достигаются в указанных точках.
и оба равенства достигаются в указанных точках.
Ответ: 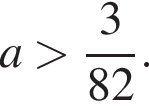
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен правильный ответ. | 4 |
| С помощью верного рассуждения получено множество значений a, отличающееся от искомого конечным числом точек. | 3 |
| С помощью верного рассуждения получены все граничные точки искомого множества значений a. | 2 |
| Верно найдена хотя бы одна граничная точка искомого множества значений a ИЛИ установлено, что исходное уравнение при всех значениях a имеет единственное решение . | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
Ответ: 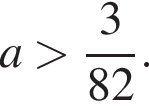
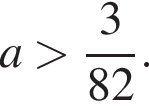
505590
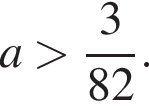
Классификатор алгебры: Неравенства с параметром
 не содержит ни одного решения неравенства
не содержит ни одного решения неравенства 




 (рис. 1). Для этого построим график уравнения
(рис. 1). Для этого построим график уравнения  — прямую, которая разбивает плоскость на две полуплоскости. Соотношению
— прямую, которая разбивает плоскость на две полуплоскости. Соотношению  (см. рис. 2).
(см. рис. 2).  Одновременно исключим из полученных результатов полосу, задаваемую неравенством
Одновременно исключим из полученных результатов полосу, задаваемую неравенством  т. е. соотношением
т. е. соотношением  (см. рис. 3).
(см. рис. 3).







 и
и  прямых
прямых  справа — прямой
справа — прямой  все граничные точки не включены. Каждая точка, принадлежащая указанной фигуре, имеет ординату, принадлежащую интервалу (0; 3). Следовательно, искомые значения параметра p заполнят весь промежуток
все граничные точки не включены. Каждая точка, принадлежащая указанной фигуре, имеет ординату, принадлежащую интервалу (0; 3). Следовательно, искомые значения параметра p заполнят весь промежуток 
 выполняется для всех х, таких, что
выполняется для всех х, таких, что 



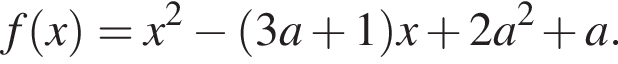
 достаточно выполнения условия:
достаточно выполнения условия: 






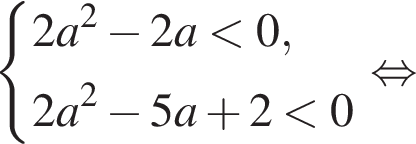




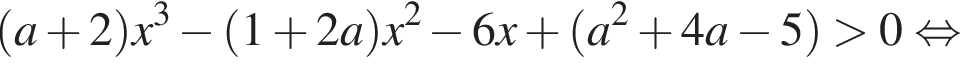

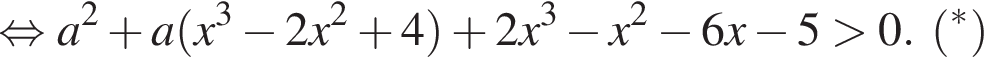



 и
и 








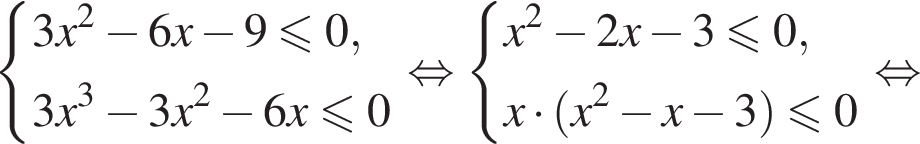





 выполняется хотя бы для одного числа x такого, что | x | < 0,01.
выполняется хотя бы для одного числа x такого, что | x | < 0,01. то подходит
то подходит  так как
так как 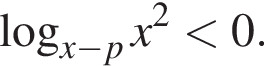

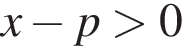 )
)


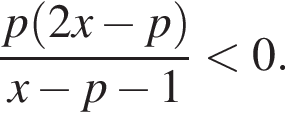
 Решая неравенство методом интервалов, получим
Решая неравенство методом интервалов, получим 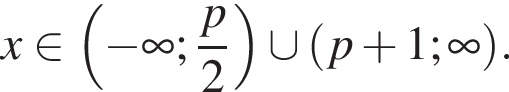 Учитывая ОДЗ, получим
Учитывая ОДЗ, получим 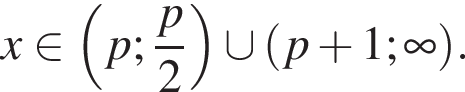

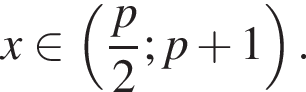 Учитывая ОДЗ, получим
Учитывая ОДЗ, получим  Нужные точки найдутся в этом множестве если
Нужные точки найдутся в этом множестве если 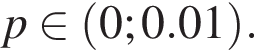


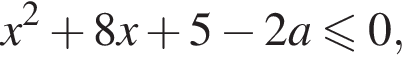 то есть
то есть  Если
Если  это вообще невозможно. Кроме того, при
это вообще невозможно. Кроме того, при  имеем
имеем  и
и  возрастает при
возрастает при  поэтому на данном промежутке нет решений неравенства.
поэтому на данном промежутке нет решений неравенства. то все возможные целые x находятся в промежутке
то все возможные целые x находятся в промежутке  поскольку
поскольку  Мы говорим лишь о возможности, поскольку не сравнивали эти значения с границами промежутка. Несомненно, при некоторых a эти точки так и не попадут на нужные промежутки.
Мы говорим лишь о возможности, поскольку не сравнивали эти значения с границами промежутка. Несомненно, при некоторых a эти точки так и не попадут на нужные промежутки.  то есть
то есть  Если
Если  это вообще невозможно. Кроме того, при
это вообще невозможно. Кроме того, при  имеем
имеем  и
и  убывает при
убывает при  поэтому на данном промежутке нет решений неравенства.
поэтому на данном промежутке нет решений неравенства. то все возможные целые x находятся в промежутке
то все возможные целые x находятся в промежутке 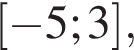 поскольку
поскольку 
 Очевидно, это невозможно при допустимых a.
Очевидно, это невозможно при допустимых a. Очевидно, это невозможно при допустимых a.
Очевидно, это невозможно при допустимых a.

 Решая это неравенство, находим
Решая это неравенство, находим 
 Решая это неравенство, находим
Решая это неравенство, находим 
 Решая это неравенство, находим
Решая это неравенство, находим 


 Очевидно, это невозможно при положительных a, а при прочих a имеем
Очевидно, это невозможно при положительных a, а при прочих a имеем  что тоже невозможно.
что тоже невозможно. Очевидно, это невозможно при допустимых a.
Очевидно, это невозможно при допустимых a. Очевидно, это невозможно при допустимых a.
Очевидно, это невозможно при допустимых a. Очевидно, это невозможно при допустимых a.
Очевидно, это невозможно при допустимых a. или
или 

 удовлетворяют неравенству
удовлетворяют неравенству 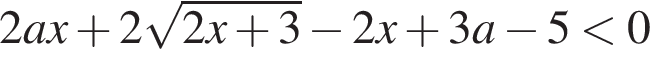 ?
?

 причем все эти значения достигаются.
причем все эти значения достигаются. при
при 


 Поэтому функция
Поэтому функция  возрастает при
возрастает при  а потом начинает убывать. Это значит, что если неравенство нарушается в какой-то точке отрезка
а потом начинает убывать. Это значит, что если неравенство нарушается в какой-то точке отрезка  (если эта точка лежит на нужном отрезке), либо при
(если эта точка лежит на нужном отрезке), либо при  откуда
откуда  Тогда
Тогда 
 Поскольку также
Поскольку также 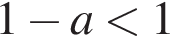 и
и  во всех подходящих нам ситуациях точка
во всех подходящих нам ситуациях точка 
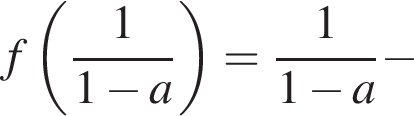
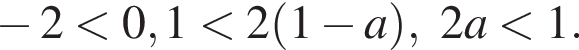






 поэтому числитель всегда имеет корни.
поэтому числитель всегда имеет корни. является корнем числителя. То есть
является корнем числителя. То есть 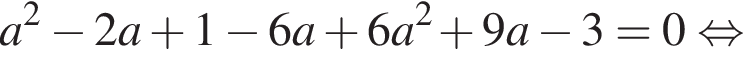



 и в нем знак меняться будет). При больших x выражение очевидно положительно, поэтому нужно только, чтобы
и в нем знак меняться будет). При больших x выражение очевидно положительно, поэтому нужно только, чтобы  и неверно при
и неверно при  Итак, подходит
Итак, подходит 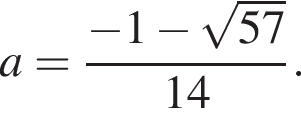
 что невозможно.
что невозможно.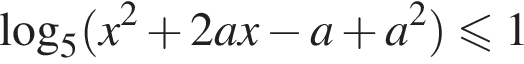 найдутся два числа, разность которых равна 1.
найдутся два числа, разность которых равна 1.



 можно взять просто
можно взять просто 








 поэтому выбирать точки надо на одном отрезке. Очевидно, такие точки есть в том и только том случае, когда длина отрезка больше 1. Будем рассматривать первый отрезок, у второго длина такая же.
поэтому выбирать точки надо на одном отрезке. Очевидно, такие точки есть в том и только том случае, когда длина отрезка больше 1. Будем рассматривать первый отрезок, у второго длина такая же.




 не имеет решений на отрезке [−3; 0].
не имеет решений на отрезке [−3; 0]. при всех
при всех  То есть чтобы
То есть чтобы  на всем этом отрезке.
на всем этом отрезке.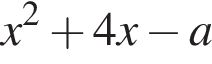 принимает при
принимает при  и это
и это  а наибольшее либо при
а наибольшее либо при  либо при
либо при  и
и  то есть
то есть 

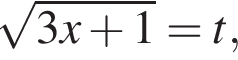
 причем все эти значения достигаются.
причем все эти значения достигаются. при
при 




 то график представляет собой параболу ветвями вниз с вершиной при
то график представляет собой параболу ветвями вниз с вершиной при  Поэтому функция
Поэтому функция  возрастает при
возрастает при  а потом начинает убывать. Это значит, что если неравенство нарушается в какой-то точке отрезка
а потом начинает убывать. Это значит, что если неравенство нарушается в какой-то точке отрезка  (если эта точка лежит на нужном отрезке), либо при
(если эта точка лежит на нужном отрезке), либо при 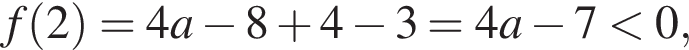 откуда
откуда 
 откуда
откуда 


 получаем ответ.
получаем ответ.



 получим из системы
получим из системы  откуда
откуда 
 то поделим оба неравенства на
то поделим оба неравенства на 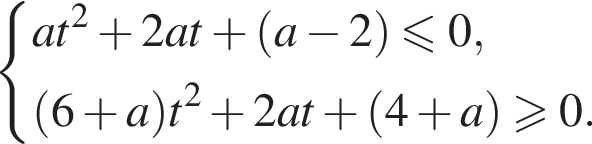



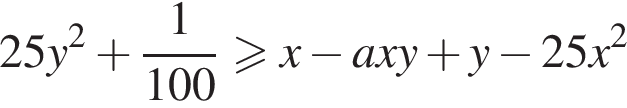
 Значит,
Значит,  и
и  откуда
откуда 
 Тогда требуется, чтобы при всех x выполнялось
Тогда требуется, чтобы при всех x выполнялось  Значит,
Значит, 

 справедливо для всех действительных x.
справедливо для всех действительных x.

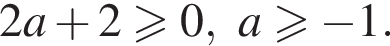







 Получим
Получим
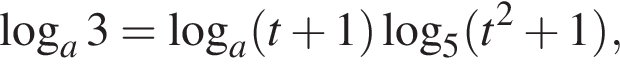
 (перешли к основанию 3)
(перешли к основанию 3) имело единственный корень. Для этого нужно, чтобы
имело единственный корень. Для этого нужно, чтобы  Но при
Но при 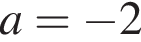 корней у исходного уравнения нет совсем (поскольку −2 не может быть основанием логарифма).
корней у исходного уравнения нет совсем (поскольку −2 не может быть основанием логарифма).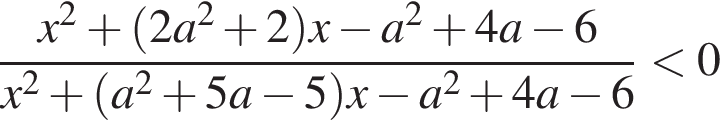 не меньше 1.
не меньше 1.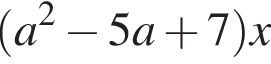 и совпадает по знаку с x. Поэтому при положительных x числитель должен быть положителен, а знаменатель отрицателен, при отрицательных x — наоборот. Заметим также, что
и совпадает по знаку с x. Поэтому при положительных x числитель должен быть положителен, а знаменатель отрицателен, при отрицательных x — наоборот. Заметим также, что  поэтому и числитель, и знаменатель имеют по два корня разных знаков. Обозначая за
поэтому и числитель, и знаменатель имеют по два корня разных знаков. Обозначая за  корни числителя, а за
корни числителя, а за  корни знаменателя имеем
корни знаменателя имеем  и
и  Итак,
Итак,  поэтому интересующая нас сумма длин интервалов есть просто
поэтому интересующая нас сумма длин интервалов есть просто 










 положительно и на него можно домножать.
положительно и на него можно домножать.




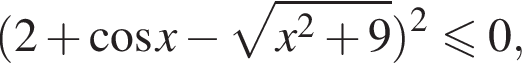



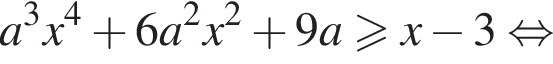



 при любых значениях а и х.
при любых значениях а и х. будем иметь:
будем иметь:  заданное неравенство для всех х не выполняется. Таким образом, искомые значения параметра а, если они есть, могут быть только строго положительными.
заданное неравенство для всех х не выполняется. Таким образом, искомые значения параметра а, если они есть, могут быть только строго положительными.















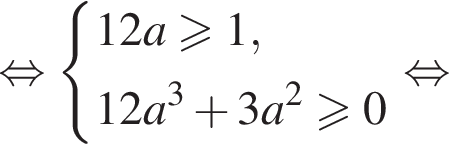

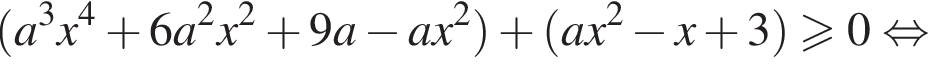
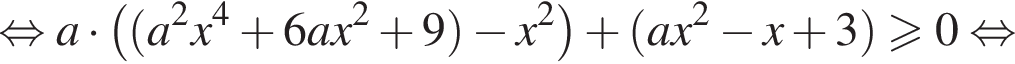



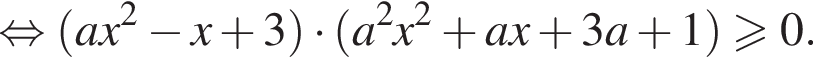

 имеет хотя бы одно решение.
имеет хотя бы одно решение. Тогда заданное неравенство будет иметь вид:
Тогда заданное неравенство будет иметь вид: 
 оба корня квадратного трехчлена отрицательны (свободный член и второй коэффициент положительны).
оба корня квадратного трехчлена отрицательны (свободный член и второй коэффициент положительны).


 т. е. число 0 лежит правее большего корня.
т. е. число 0 лежит правее большего корня. 
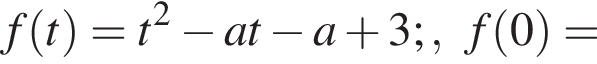





 не равно значению выражения
не равно значению выражения 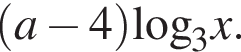
 будет выполнено равенство
будет выполнено равенство 
 Тогда
Тогда 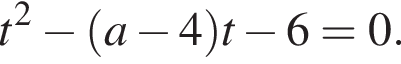 Поскольку
Поскольку  рассматриваемый промежуток для t будет
рассматриваемый промежуток для t будет  будет выполнено равенство
будет выполнено равенство  равен 1, т. е. положителен; ограничений на значения а нет;
равен 1, т. е. положителен; ограничений на значения а нет;  при любом значении параметра, значит,
при любом значении параметра, значит, 



 т. е.
т. е. 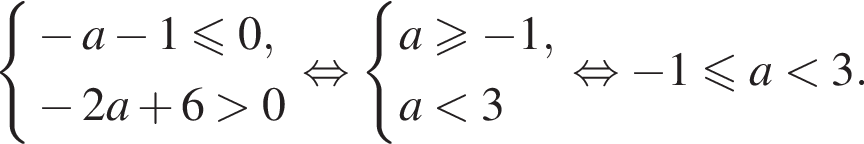
 найдётся
найдётся  или
или 
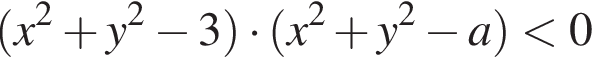 имеет ровно четыре целочисленных решения (x; у).
имеет ровно четыре целочисленных решения (x; у).

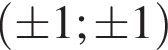 и положительно во всех остальных точках.
и положительно во всех остальных точках. что дает уже 8 решений.
что дает уже 8 решений. Выражение во второй скобке неположительно только в точках
Выражение во второй скобке неположительно только в точках 
 Выражение во второй скобке неположительно только в точках
Выражение во второй скобке неположительно только в точках 
 решений нет.
решений нет. Выражение во второй скобке отрицательно только в точках.
Выражение во второй скобке отрицательно только в точках.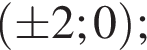


 что дает уже 8 решений.
что дает уже 8 решений.



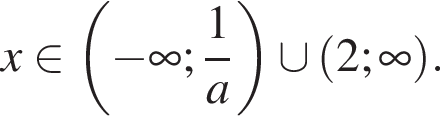

 поэтому ответ
поэтому ответ 

 ответ
ответ 
 при всех
при всех  то есть
то есть 
 при всех
при всех  то есть
то есть  имеет единственное целочисленное решение. Для найденных значений a выпишите это решение.
имеет единственное целочисленное решение. Для найденных значений a выпишите это решение. то есть
то есть 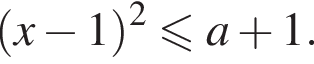
 то решений нет.
то решений нет.  то единственное решение
то единственное решение  то единственное целое решение
то единственное целое решение 
 то есть два подходящих целых решения
то есть два подходящих целых решения 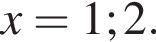 Если
Если 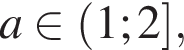 то есть одно подходящее целое решение
то есть одно подходящее целое решение 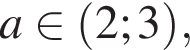 то подходящих целых решений нет.
то подходящих целых решений нет. 
 то есть
то есть 
 то единственное целое решение
то единственное целое решение  то
то  поэтому есть целые решения
поэтому есть целые решения  из которых подходит только
из которых подходит только  то подходящих решений нет.
то подходящих решений нет.  то
то  поэтому есть целые решения
поэтому есть целые решения  из которых подходит только
из которых подходит только 
 но они все не подходят.
но они все не подходят.  при
при 
 при
при  при
при 
 выполняется для любых
выполняется для любых 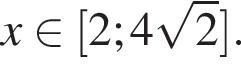
 Тогда задачу можно будет переформулировать так: найдите все значения а, при каждом из которых неравенство
Тогда задачу можно будет переформулировать так: найдите все значения а, при каждом из которых неравенство  выполняется для любых
выполняется для любых 




 Она (функция) квадратичная, график ее — парабола с ветвями, направленными вверх. Для того чтобы числа 1 и
Она (функция) квадратичная, график ее — парабола с ветвями, направленными вверх. Для того чтобы числа 1 и 

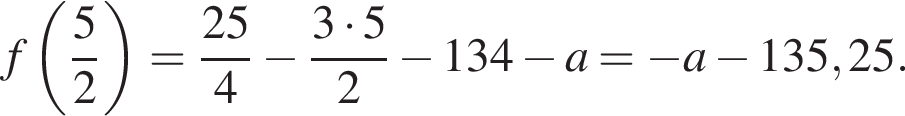




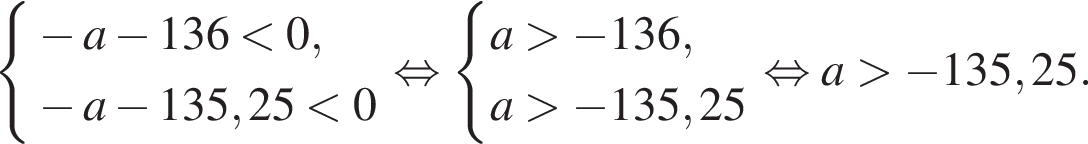




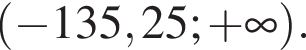
 содержит ровно четыре целых значения x.
содержит ровно четыре целых значения x. Прямые, задаваемые уравнениями
Прямые, задаваемые уравнениями  разбивают плоскость хОа на четыре области. Раскроем модули, на каждой из этих областей и построим на этих областях график неравенства (см. ниже).
разбивают плоскость хОа на четыре области. Раскроем модули, на каждой из этих областей и построим на этих областях график неравенства (см. ниже). или
или 
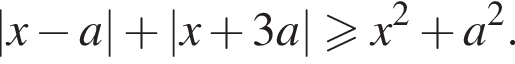 Раскрывая модули, получаем четыре области.
Раскрывая модули, получаем четыре области.






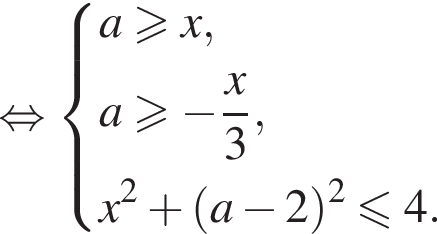








 ограниченную прямыми
ограниченную прямыми  Заметим, что окружность ω1, являющаяся границей круга, пересекает ось абсцисс в точках
Заметим, что окружность ω1, являющаяся границей круга, пересекает ось абсцисс в точках  и
и  Найдем координаты точек пересечения данной окружности с указанными прямыми. Для прямой
Найдем координаты точек пересечения данной окружности с указанными прямыми. Для прямой 


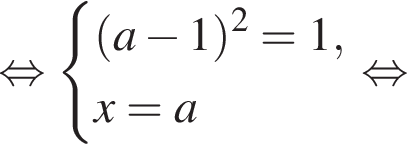


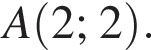
 находим:
находим: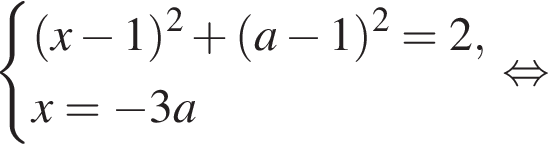





 ограниченную прямыми
ограниченную прямыми 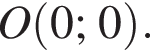 Найдем координаты точек пересечения данной окружности с указанными прямыми. Для прямой
Найдем координаты точек пересечения данной окружности с указанными прямыми. Для прямой 










 является его решением:
является его решением: 



 и
и  при
при  при условии
при условии 
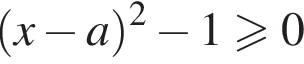 при условии
при условии 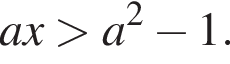
 при условии
при условии 
 или
или  при условии
при условии 
 при
при  это дает
это дает  или
или 
 Неравенство тогда равносильно
Неравенство тогда равносильно  при условии
при условии 
 при условии
при условии 
 при условии
при условии  при условии
при условии  ) или
) или 

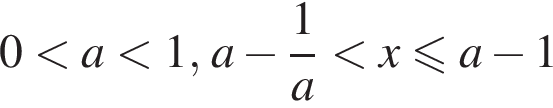 или
или  решений нет,
решений нет,



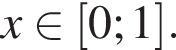 Заметим, что
Заметим, что  Получим
Получим
 Возможны два случая.
Возможны два случая. Тогда точка
Тогда точка 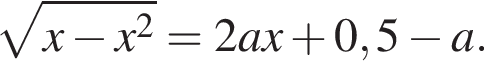 Нетрудно видеть, что этого не происходит ни при каком a.
Нетрудно видеть, что этого не происходит ни при каком a. где числа t,
где числа t,  Получаем систему
Получаем систему

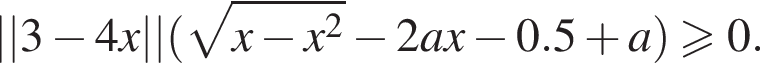
 отличается от нашего только (возможно) наличием точки
отличается от нашего только (возможно) наличием точки  Преобразуя его, получаем
Преобразуя его, получаем 

 (возможно, посторонний корень). Поэтому множество решений неравенства должно быть отрезком от одной из точек
(возможно, посторонний корень). Поэтому множество решений неравенства должно быть отрезком от одной из точек  до другой и содержать точку
до другой и содержать точку 
 Докажем, что такие a подходят.
Докажем, что такие a подходят.  имеем неравенство
имеем неравенство  именно с таким множеством решений.
именно с таким множеством решений.
 функция
функция  возрастает, а функция
возрастает, а функция 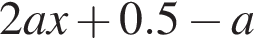 убывает. Поскольку в точке
убывает. Поскольку в точке 

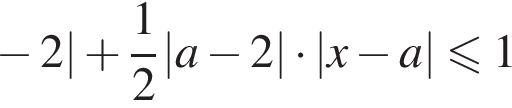


 (это не повлияет на число решений). Получим
(это не повлияет на число решений). Получим
 причем
причем 

 Докажем, что такие значения a действительно подходят. Подставляя их в неравенство, получим
Докажем, что такие значения a действительно подходят. Подставляя их в неравенство, получим
 неравенство сведется к
неравенство сведется к  — нет решений.
— нет решений. неравенство сведется к
неравенство сведется к  — нет решений.
— нет решений. неравенство сведется к
неравенство сведется к  — решения только
— решения только 
 на отрезке
на отрезке 

 и отрицательна на
и отрицательна на  отрицательна на
отрицательна на  положительна на
положительна на  поэтому наибольшее значение достигается при
поэтому наибольшее значение достигается при 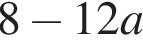 (второе больше при
(второе больше при 
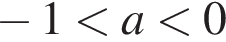 производная положительна на
производная положительна на 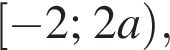 отрицательна на
отрицательна на  положительна на
положительна на  то есть равно
то есть равно  производная отрицательна на
производная отрицательна на 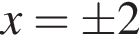 и равно 20 или 4 — значит, 20.
и равно 20 или 4 — значит, 20. Очевидно, надо выбирать
Очевидно, надо выбирать 
 при
при 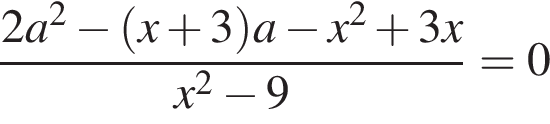

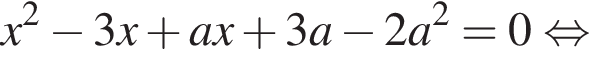


 то есть
то есть  тогда
тогда  и уравнение имеет единственный корень
и уравнение имеет единственный корень  тогда
тогда  тогда
тогда  или
или 




 получим уравнение
получим уравнение 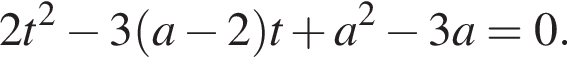 Оно раскладывается на множители
Оно раскладывается на множители  и имеет корни
и имеет корни 
 убывает из
убывает из  и неограниченно возрастает при
и неограниченно возрастает при 
 имеет наибольшее количество решений на отрезке
имеет наибольшее количество решений на отрезке  Чему равно это количество?
Чему равно это количество? и обозначим
и обозначим  Получим:
Получим:





 имеет на промежутке вида
имеет на промежутке вида  одно решение при
одно решение при  два решения при
два решения при  и ни одного решения при прочих
и ни одного решения при прочих  уравнение может иметь максимум 8 решений: два несовпадающих корня, дающих по 2 решения и на
уравнение может иметь максимум 8 решений: два несовпадающих корня, дающих по 2 решения и на  и на
и на  Восемь решений возможны и в нашем случае. Для этого необходимо, чтобы на промежутке
Восемь решений возможны и в нашем случае. Для этого необходимо, чтобы на промежутке 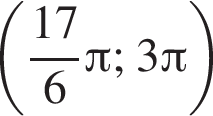 решений не было. Тогда
решений не было. Тогда 




 Ясно, что количество решений от этого не изменится — по каждой паре x и y однозначно строится пара u и
Ясно, что количество решений от этого не изменится — по каждой паре x и y однозначно строится пара u и 

 (если
(если  и радиусом
и радиусом  которая пересекает окружность в точках
которая пересекает окружность в точках  (можно проверить подстановкой). Наконец, последнее уравнение задаёт прямую, проходящую через начало координат (см. рис.).
(можно проверить подстановкой). Наконец, последнее уравнение задаёт прямую, проходящую через начало координат (см. рис.). до этой прямой должно быть равно 2. То есть
до этой прямой должно быть равно 2. То есть  Отсюда:
Отсюда:




 прямая не пересекает окружность. При
прямая не пересекает окружность. При  есть одна общая точка. При
есть одна общая точка. При  есть две общие точки. При
есть две общие точки. При 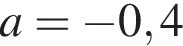 есть одна общая точка (вторая выколота). При
есть одна общая точка (вторая выколота). При  есть одна общая точка (вторая не в той полуплоскости). При
есть одна общая точка (вторая не в той полуплоскости). При 
 имеет ровно три корня. Для каждого а укажите корни.
имеет ровно три корня. Для каждого а укажите корни. то есть
то есть  Разберем теперь случаи.
Разберем теперь случаи. оно имеет корни
оно имеет корни 
 Будем искать положительные корни. Избавляясь от модуля и деля на x, имеем
Будем искать положительные корни. Избавляясь от модуля и деля на x, имеем  Поскольку при подстановке
Поскольку при подстановке  Будем искать положительные корни. Избавляясь от модуля и деля на x, имеем
Будем искать положительные корни. Избавляясь от модуля и деля на x, имеем  Домножим на знаменатель и обозначим
Домножим на знаменатель и обозначим  Получим
Получим  откуда
откуда 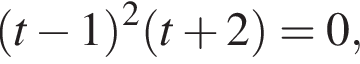 что дает
что дает 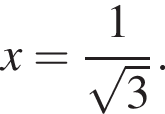 Как раз один положительный корень, общее число корней — три.
Как раз один положительный корень, общее число корней — три.
 при
при 
 при
при  (поскольку
(поскольку 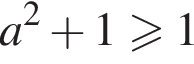 ). Тогда второе превращается в
). Тогда второе превращается в 
 и
и  Чтобы не было решений, нужно, чтобы эти числа не могли быть значениями косинуса. Отсюда
Чтобы не было решений, нужно, чтобы эти числа не могли быть значениями косинуса. Отсюда 


 откуда
откуда  Кроме того,
Кроме того, 



 Домножим на
Домножим на 





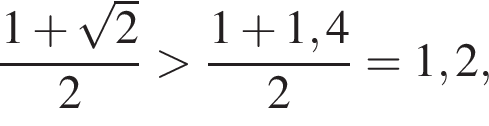 получим ответ
получим ответ 


 Значит, уравнение
Значит, уравнение  должно иметь ровно одно решение на отрезке
должно иметь ровно одно решение на отрезке  в точках
в точках 



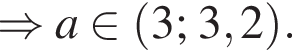
 оно имеет один подходящий корень.
оно имеет один подходящий корень. уравнение принимает вид
уравнение принимает вид  поэтому его сумма корней равна 6,4. Один из корней равен 6, поэтому второй равен 0,4. Эта ситуация нас устраивает.
поэтому его сумма корней равна 6,4. Один из корней равен 6, поэтому второй равен 0,4. Эта ситуация нас устраивает.
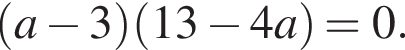
 (тогда есть один корень, равный 3,25).
(тогда есть один корень, равный 3,25).










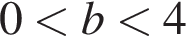 (
( имеет единственный корень меньший 2;
имеет единственный корень меньший 2;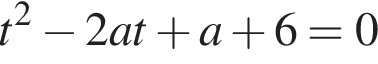 имеет два корня большие 2.
имеет два корня большие 2. Значит, квадратное уравнение имеет единственный корень
Значит, квадратное уравнение имеет единственный корень 
 что подходит. (Исходное уравнение имеет четыре корня)
что подходит. (Исходное уравнение имеет четыре корня)




 Исследуем функцию
Исследуем функцию  Она четная, убывает на
Она четная, убывает на  она принимает по 4 раза, значение 2 — три раза, а значения из промежутка
она принимает по 4 раза, значение 2 — три раза, а значения из промежутка  она принимает по 2 раза. Рассмотрим квадратное уравнение
она принимает по 2 раза. Рассмотрим квадратное уравнение  Каждый его корень дает 2, 3 или 4 корня исходного уравнения. Значит, либо оба корня должны давать по два, либо корень должен быть единственным и давать 4.
Каждый его корень дает 2, 3 или 4 корня исходного уравнения. Значит, либо оба корня должны давать по два, либо корень должен быть единственным и давать 4.
 При
При  имеем
имеем  при
при 
 правее двойки и значение данного трехчлена при
правее двойки и значение данного трехчлена при 
 Получаем
Получаем 
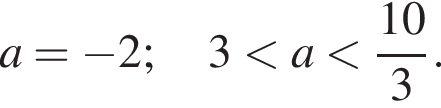


 имеет корень на интервале
имеет корень на интервале  то уравнение
то уравнение  (этот корень) будет иметь на данном промежутке минимум два корня. Если оно имеет корень, по модулю больший <1, по нему не подберется ни одного корня
(этот корень) будет иметь на данном промежутке минимум два корня. Если оно имеет корень, по модулю больший <1, по нему не подберется ни одного корня 


 и будет иметь еще корень 0. Не подходит.
и будет иметь еще корень 0. Не подходит. и будет иметь только корень 1. Подходит.
и будет иметь только корень 1. Подходит. и будет иметь еще корень -3. Подходит.
и будет иметь еще корень -3. Подходит.

 поэтому одно из этих чисел ноль. Функция непрерывна на всей вещественной оси поэтому принимает все промежуточные значения, поэтому вторым значением может быть только
поэтому одно из этих чисел ноль. Функция непрерывна на всей вещественной оси поэтому принимает все промежуточные значения, поэтому вторым значением может быть только  имеет корень, а уравнения
имеет корень, а уравнения  и
и  корней не имеют. Уравнение
корней не имеют. Уравнение  имеет корни, а уравнения
имеет корни, а уравнения 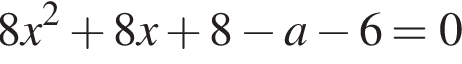 и
и 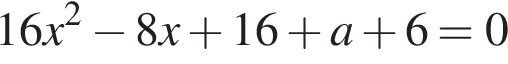 корней не имеет. Вычислим дискриминанты:
корней не имеет. Вычислим дискриминанты:


 эти два целых числа 0 и 1.
эти два целых числа 0 и 1. корней не имеют. Уравнение
корней не имеют. Уравнение  корней не имеет. Вычислим дискриминанты:
корней не имеет. Вычислим дискриминанты:
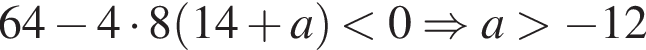

 эти два целых числа 0 и
эти два целых числа 0 и  с целыми коэффициентами имеет три различных корня. Оказалось, что первый корень является синусом, второй — косинусом, а третий — тангенсом одного и того же угла. Найдите все такие уравнения.
с целыми коэффициентами имеет три различных корня. Оказалось, что первый корень является синусом, второй — косинусом, а третий — тангенсом одного и того же угла. Найдите все такие уравнения.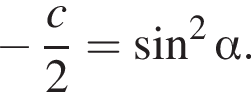 Значит, возможные значения для
Значит, возможные значения для  Тогда
Тогда  и есть совпадающие корни.
и есть совпадающие корни.  имеем:
имеем: 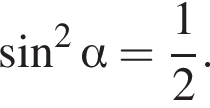 Тогда
Тогда 

 Их сумма равна
Их сумма равна  Значит,
Значит, 
 имеем:
имеем:  Тогда
Тогда  а
а 

 неположительно. Первое уравнение дает
неположительно. Первое уравнение дает





 Ясно, что она может пересекать построенные два луча и прямую один раз только если она не пересекает интервал от
Ясно, что она может пересекать построенные два луча и прямую один раз только если она не пересекает интервал от 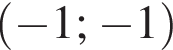 до
до  который нам подходит) и не параллельна
который нам подходит) и не параллельна 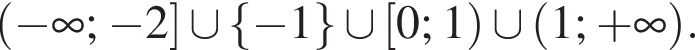

 Поэтому оно задает четыре дуги окружностей радиуса
Поэтому оно задает четыре дуги окружностей радиуса  (дуги, а не окружности целиком, потому что нужно следить за знаками при раскрытии модулей). Все эти окружности проходят через начало координат, поэтому точка
(дуги, а не окружности целиком, потому что нужно следить за знаками при раскрытии модулей). Все эти окружности проходят через начало координат, поэтому точка  Это прямая, проходящая через точку
Это прямая, проходящая через точку 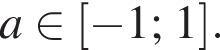 Кроме того, при
Кроме того, при 
 при
при 

 до прямой равно
до прямой равно 








 (в ответ добавлены числа вида
(в ответ добавлены числа вида 
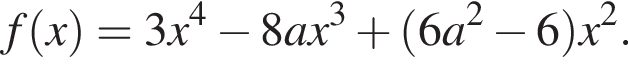


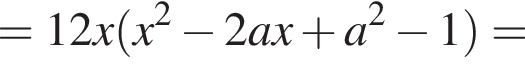




 Разберем случаи их расположения на прямой.
Разберем случаи их расположения на прямой. это точка 0, при
это точка 0, при  это точка
это точка  При
При  производная неположительна при
производная неположительна при  и неотрицательна при
и неотрицательна при  поэтому точки максимума нет.
поэтому точки максимума нет. это точка 0; при
это точка 0; при  точки максимума нет.
точки максимума нет.


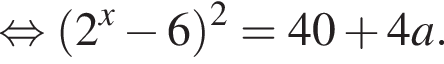


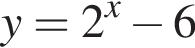 принимает значения от −4 невключительно до 2 включительно, причем не принимает значения
принимает значения от −4 невключительно до 2 включительно, причем не принимает значения  принимает по одному разу значения 0 и из промежутка
принимает по одному разу значения 0 и из промежутка 
 либо
либо 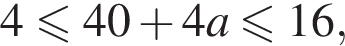 откуда
откуда 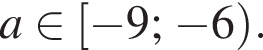



 все слагаемые, кроме последнего, сохранятся, а последнее увеличится. Заметим также, что если заменить одновременно a на
все слагаемые, кроме последнего, сохранятся, а последнее увеличится. Заметим также, что если заменить одновременно a на 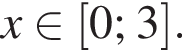 Тогда модуль не нужен и функция принимает вид
Тогда модуль не нужен и функция принимает вид 
 Возьмем ее производную — наибольшее значение может быть либо в ее корнях, либо в концах отрезка
Возьмем ее производную — наибольшее значение может быть либо в ее корнях, либо в концах отрезка 
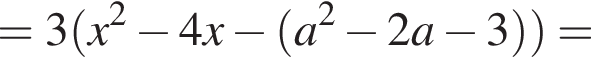

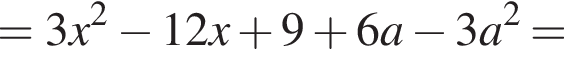
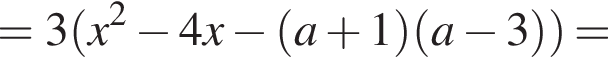






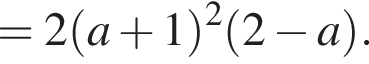


 то есть
то есть  Наконец,
Наконец, 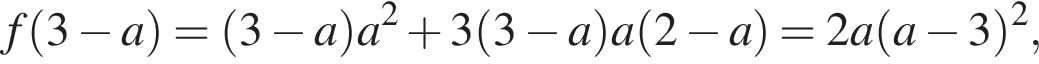




 то есть
то есть  Теперь сравним значения функции в этих точках. Напомним, что
Теперь сравним значения функции в этих точках. Напомним, что 








 наибольшее, если
наибольшее, если 







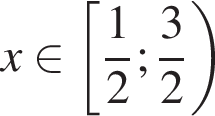 (и еще при
(и еще при  и
и  Это имеет смысл только на промежутке
Это имеет смысл только на промежутке 


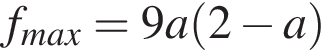
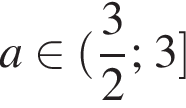



 при
при  при
при  при
при  при
при  при
при  при
при  при
при 






 поэтому нам подойдет только
поэтому нам подойдет только 

 уравнение примет вид
уравнение примет вид  его корни 1 и 3 — не подходит.
его корни 1 и 3 — не подходит.
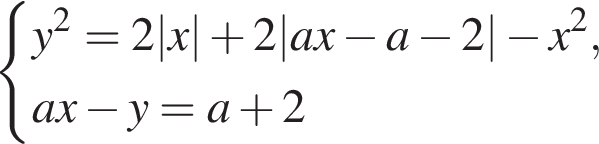
 и подставим в первое:
и подставим в первое:


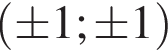 (дуги, а не окружности целиком, потому что нужно следить за знаками при раскрытии модулей). Все эти окружности проходят через начало координат, поэтому точка
(дуги, а не окружности целиком, потому что нужно следить за знаками при раскрытии модулей). Все эти окружности проходят через начало координат, поэтому точка 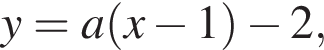 то есть задает прямую, проходящую через точку
то есть задает прямую, проходящую через точку 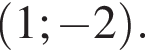
 до прямой было равно
до прямой было равно 





 и давать два решения (только в четвертой четверти), пока либо не пройдет через точку
и давать два решения (только в четвертой четверти), пока либо не пройдет через точку  то есть
то есть 
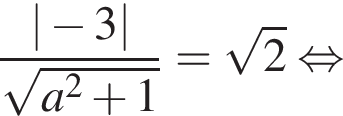



 (коснуться дуги во второй четверти она не может). Дальше их снова будет два (на второй и четвертой дугах) и так будет все время, кроме случая, когда прямая проходит через начало координат — отдельную точку нашей фигуры. Там решений будет три. Это произойдет при
(коснуться дуги во второй четверти она не может). Дальше их снова будет два (на второй и четвертой дугах) и так будет все время, кроме случая, когда прямая проходит через начало координат — отдельную точку нашей фигуры. Там решений будет три. Это произойдет при 

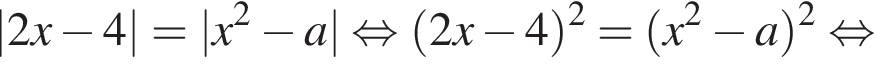



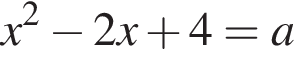 и
и 
 будет парабола с вершиной в точке
будет парабола с вершиной в точке 

 будет парабола с вершиной в точке
будет парабола с вершиной в точке  Поэтому при
Поэтому при  по одному разу (
по одному разу ( ). Итак, количество положительных корней:
). Итак, количество положительных корней: 

 Заметим, что условие положительности a нам не пригодилось.
Заметим, что условие положительности a нам не пригодилось.

 Заметим сразу, что
Заметим сразу, что  поэтому
поэтому 
 При всех таких t должно выполняться неравенство
При всех таких t должно выполняться неравенство
 — парабола, ветви которой направлены вверх, поэтому ее наименьшее значение на множестве
— парабола, ветви которой направлены вверх, поэтому ее наименьшее значение на множестве  достигается либо в точке
достигается либо в точке  если абсцисса вершины лежит в множестве
если абсцисса вершины лежит в множестве  ), либо, наконец, не достигается, потому что
), либо, наконец, не достигается, потому что  функция возрастает на всем нашем множестве и могла бы иметь наименьшее значение при
функция возрастает на всем нашем множестве и могла бы иметь наименьшее значение при 













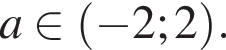
 то есть к
то есть к  Соответственно, оно лишь запрещает промежуток
Соответственно, оно лишь запрещает промежуток 
 Здесь нестрогое неравенство, поскольку брать саму точку
Здесь нестрогое неравенство, поскольку брать саму точку  поэтому неравенство написать нужно. Окончательно:
поэтому неравенство написать нужно. Окончательно: 


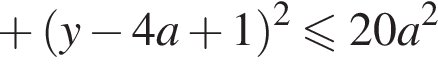


 Второе - круг радиуса
Второе - круг радиуса  с центром в
с центром в  (возможно вырождается в точку, при
(возможно вырождается в точку, при 



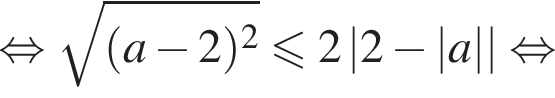

 что верно. При нуле один из кругов точка. При отрицательных a раскроем внутренний модуль и возведем в квадрат (обе части неотрицательны, поэтому так делать можно):
что верно. При нуле один из кругов точка. При отрицательных a раскроем внутренний модуль и возведем в квадрат (обе части неотрицательны, поэтому так делать можно):



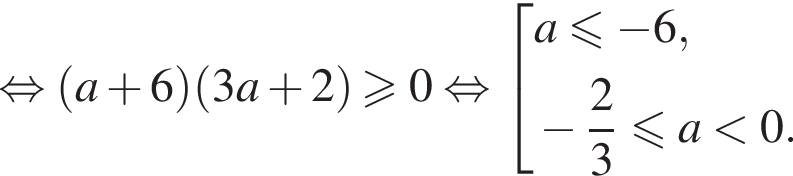
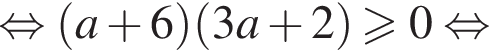



 то есть
то есть  Кроме того,
Кроме того,  При таких x рационализируем неравенство:
При таких x рационализируем неравенство:



 и отрицателен при
и отрицателен при  Знаменатель при отрицательных a положителен всегда, при
Знаменатель при отрицательных a положителен всегда, при  и положителен при
и положителен при 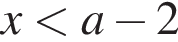 или
или  Тем самым нужно сравнивать
Тем самым нужно сравнивать  с
с 


 имеем:
имеем:  поэтому ответ
поэтому ответ  (предыдущий случай можно будет объединить с этим);
(предыдущий случай можно будет объединить с этим); и знаки числителя и знаменателя одинаковы всегда, решений нет;
и знаки числителя и знаменателя одинаковы всегда, решений нет; имеем
имеем  откуда ответ
откуда ответ 
 ответ такой же;
ответ такой же;

 при
при  при
при  ответ
ответ  при
при 








 а число
а число  там лежать не должно. Первые два числа лежат на этом интервале при
там лежать не должно. Первые два числа лежат на этом интервале при  (дальше нельзя, попадет и третье, раньше нельзя, попадет 0,890625). Второе и третье числа там лежат при
(дальше нельзя, попадет и третье, раньше нельзя, попадет 0,890625). Второе и третье числа там лежат при  Третье и четвертое числа там лежат при
Третье и четвертое числа там лежат при 




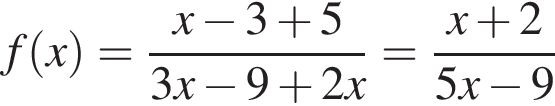 при
при  при
при 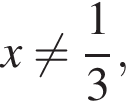

 То есть нас интересует, какие значения принимает функция
То есть нас интересует, какие значения принимает функция 









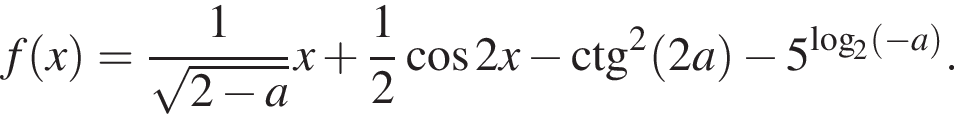


 имеет на отрезке
имеет на отрезке 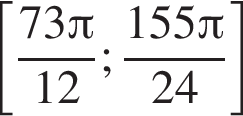 ровно два корня?
ровно два корня?

 будем иметь:
будем иметь:
 до
до  ) и потом, убывая, принимает еще раз значения до
) и потом, убывая, принимает еще раз значения до  и потом какие-то еще меньшие значения. Значит, ровно два раза одно значение он принимает, только если это значение попадает в промежуток
и потом какие-то еще меньшие значения. Значит, ровно два раза одно значение он принимает, только если это значение попадает в промежуток  Имеем:
Имеем:



 Выколотая точка возникла из-за ограничений на котангенс, а 1 заменилась на 0 из-за условия
Выколотая точка возникла из-за ограничений на котангенс, а 1 заменилась на 0 из-за условия 




 нужно, чтобы угловой коэффициент касательной равнялся −2, поэтому
нужно, чтобы угловой коэффициент касательной равнялся −2, поэтому  и
и 




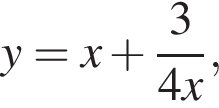 уравнение
уравнение  не должно иметь решений. Перепишем его в виде
не должно иметь решений. Перепишем его в виде  Это уравнение не должно иметь корней. Исследуем функцию
Это уравнение не должно иметь корней. Исследуем функцию  Очевидно, при положительных x она положительна, при
Очевидно, при положительных x она положительна, при  а значение этой функции в точке
а значение этой функции в точке  единственная возможность — взять
единственная возможность — взять  (дискриминант отрицательный), поэтому:
(дискриминант отрицательный), поэтому: 


 (то есть
(то есть  или
или  чтобы
чтобы  был определен (концы отрезка запрещены, эти корни уже есть).
был определен (концы отрезка запрещены, эти корни уже есть).





 Отметим, что аргумент косинуса пробегает значения
Отметим, что аргумент косинуса пробегает значения 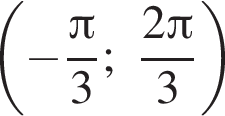 и косинус там принимает один раз значение 1 и значения в промежутке
и косинус там принимает один раз значение 1 и значения в промежутке  и два раза принимает значения в промежутке
и два раза принимает значения в промежутке  Значит, уравнение
Значит, уравнение 
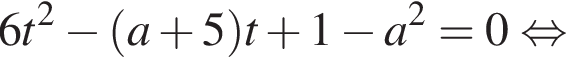



 при
при  (по
(по  при
при  (по
(по  при
при  (по
(по  при
при  (по
(по 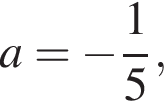 оно дает один корень исходного уравнения и нам не подходит. Если первое t дает два корня, то второе — не меньше одного и наоборот, как видно из рассмотрения промежутков. Остается только случай, когда оба дают по одному корню.
оно дает один корень исходного уравнения и нам не подходит. Если первое t дает два корня, то второе — не меньше одного и наоборот, как видно из рассмотрения промежутков. Остается только случай, когда оба дают по одному корню.

 принимает все значения. Если
принимает все значения. Если 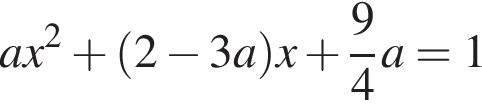 при
при 






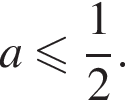
 при
при 





 Уравнение примет вид:
Уравнение примет вид: 
 ), это возможно в том и только том случае, когда
), это возможно в том и только том случае, когда  Значит, именно это уравнение должно иметь два корня. Имеем:
Значит, именно это уравнение должно иметь два корня. Имеем:


 то есть при
то есть при 


 один корень. При прочих a это квадратное уравнение, вычислим дискриминант:
один корень. При прочих a это квадратное уравнение, вычислим дискриминант: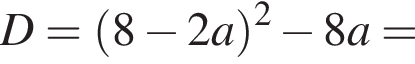

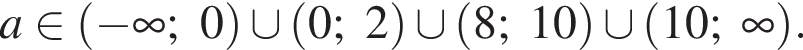


 то есть
то есть  Это уравнение окружности с центром
Это уравнение окружности с центром 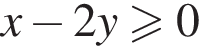
 то есть
то есть  Это уравнение окружности с центром
Это уравнение окружности с центром  и радиусом
и радиусом 
 На рисунке изображены различные положения прямой. Из рисунка видно, что нам подходят
На рисунке изображены различные положения прямой. Из рисунка видно, что нам подходят  Осталось их найти. При этом a прямая касается нижней окружности, то есть расстояние от центра окружности до этой прямой равно
Осталось их найти. При этом a прямая касается нижней окружности, то есть расстояние от центра окружности до этой прямой равно 


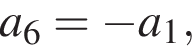

 Подставляя это в первое уравнение, получим:
Подставляя это в первое уравнение, получим: 
 поэтому
поэтому  Из симметрии
Из симметрии 

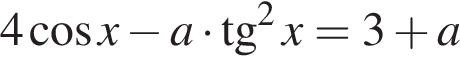 имеет на отрезке
имеет на отрезке  то есть
то есть  при этом
при этом  тогда уравнение
тогда уравнение  должно иметь ровно один корень на множестве
должно иметь ровно один корень на множестве 
 Ее производная
Ее производная 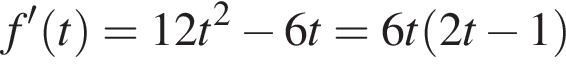 отрицательна при
отрицательна при  и положительна при
и положительна при  Значит, функция возрастает на
Значит, функция возрастает на 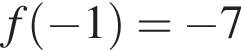 до
до  затем убывает до
затем убывает до 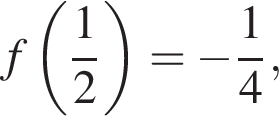 затем снова возрастает до
затем снова возрастает до  Поэтому она принимает один раз такие значения —
Поэтому она принимает один раз такие значения —  Мы включаем
Мы включаем  имеет два корня (
имеет два корня (



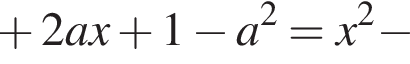
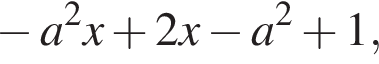




 Подставим их.
Подставим их.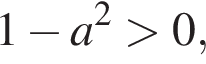 поэтому этот корень есть при
поэтому этот корень есть при 



 получаем
получаем 
 поэтому корень есть при
поэтому корень есть при 




 Ясно что
Ясно что  то есть
то есть  то модуль на всем промежутке раскрывается с одним и тем же знаком,
то модуль на всем промежутке раскрывается с одним и тем же знаком,  Тогда наша функция — квадратный трехчлен, он принимает наибольшее значение либо при
Тогда наша функция — квадратный трехчлен, он принимает наибольшее значение либо при  (если эта точка лежит на интервале!), либо на концах отрезка. Значит, нужно сравнить числа:
(если эта точка лежит на интервале!), либо на концах отрезка. Значит, нужно сравнить числа:
 при
при 
 при
при 
 Во втором
Во втором  график — парабола ветвями вниз, поэтому наибольшее значение именно в вершине и равно
график — парабола ветвями вниз, поэтому наибольшее значение именно в вершине и равно  то функция устроена так:
то функция устроена так: 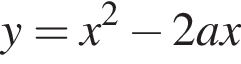 при
при  и
и  при
при  На промежутке
На промежутке  следовательно, функция возрастает, а на промежутке
следовательно, функция возрастает, а на промежутке  имеет наибольшее значение при
имеет наибольшее значение при 





 наибольшее значение
наибольшее значение  а при
а при 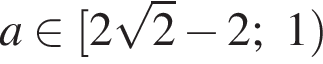 наибольшее значение
наибольшее значение  будет
будет 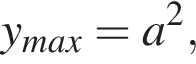 при прочих a
при прочих a 



 Преобразуем уравнение:
Преобразуем уравнение:


 или
или 
 или
или 
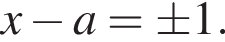
 у него больше двух корней. Далее считаем
у него больше двух корней. Далее считаем 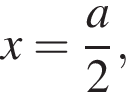










 Он определен при всех
Он определен при всех 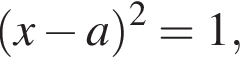

 они будут и корнями уравнения, если подходят в ОДЗ корня
они будут и корнями уравнения, если подходят в ОДЗ корня 
 или
или 
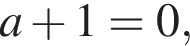
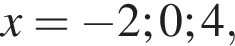

 как раз три корня;
как раз три корня;


 (
(
 верно неравенство
верно неравенство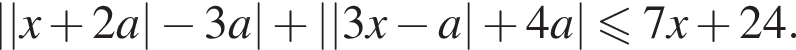







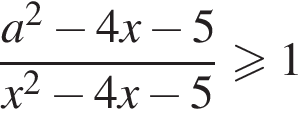 имеет ровно четыре целочисленных решения. Для каждого такого укажите эти решения.
имеет ровно четыре целочисленных решения. Для каждого такого укажите эти решения. Сразу отметим, что при замене a на
Сразу отметим, что при замене a на  там пять целых точек.
там пять целых точек.  Тогда
Тогда  там четыре целые точки —
там четыре целые точки — 
 там четыре целые точки —
там четыре целые точки — 
 Тогда
Тогда  Нетрудно видеть, что при целых a там по
Нетрудно видеть, что при целых a там по  там четыре целые точки —
там четыре целые точки — 
 Тогда
Тогда  там четыре целые точки —
там четыре целые точки — 

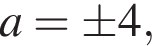








 тогда неравенство примет вид
тогда неравенство примет вид 

 то можно немного увеличить t и получить другое решение. Значит,
то можно немного увеличить t и получить другое решение. Значит, 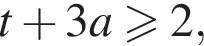 поэтому
поэтому  При меньших a можно взять
При меньших a можно взять  для отрицательных a и получить решение, для которого
для отрицательных a и получить решение, для которого 








 имеет корни на промежутке
имеет корни на промежутке  то в этом корне получаем
то в этом корне получаем  принимает на данном промежутке значения в промежутке
принимает на данном промежутке значения в промежутке  то есть
то есть 
 Правая часть принимает значения на промежутке
Правая часть принимает значения на промежутке  поэтому неравенство имеет решения при
поэтому неравенство имеет решения при 
 это не может быть верно, правая часть не меньше
это не может быть верно, правая часть не меньше 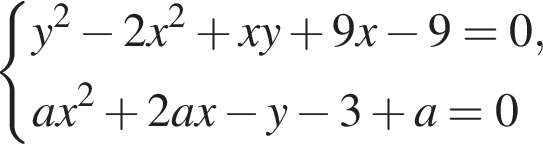

 или
или  Значит, уравнения
Значит, уравнения 
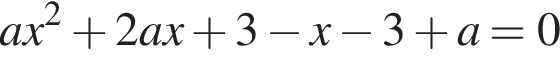
 то есть
то есть  и
и  поэтому при
поэтому при  и
и 
 и
и 
 и
и 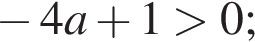




 Отметим сразу, что при
Отметим сразу, что при 

 Далее:
Далее:


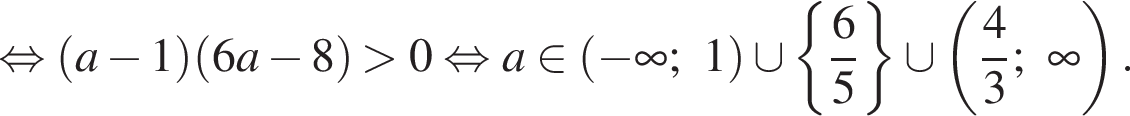


 Далее:
Далее:






 Разделим уравнение на
Разделим уравнение на  и обозначим
и обозначим  Имеем:
Имеем: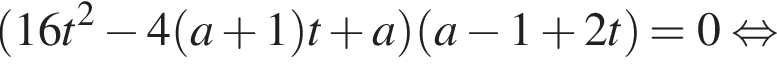



 равносильно уравнению
равносильно уравнению  и потому имеет один корень при
и потому имеет один корень при  (то есть при
(то есть при 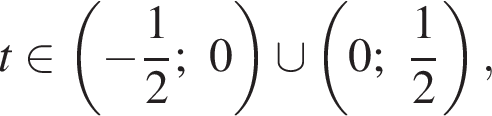 один корень при
один корень при  и не имеет корней при прочих
и не имеет корней при прочих  и два из них совпадают. Первые совпадают при
и два из них совпадают. Первые совпадают при  и не дает корней при
и не дает корней при  Третье дает
Третье дает  и
и  Значит, нам подходит промежуток
Значит, нам подходит промежуток 
 Это получается при
Это получается при 

 Тогда либо
Тогда либо  либо
либо  поэтому решения будут лишь при
поэтому решения будут лишь при  Заметим далее, что при подстановке вместо x любого числа в оба уравнения легко найти два значения a, при которых x будет корнем. Значит, полученные значения должны совпасть, то есть x годится сразу в оба уравнения. Решим систему
Заметим далее, что при подстановке вместо x любого числа в оба уравнения легко найти два значения a, при которых x будет корнем. Значит, полученные значения должны совпасть, то есть x годится сразу в оба уравнения. Решим систему
 то есть
то есть  Оно получается лишь при
Оно получается лишь при 


 Получим:
Получим:
 что верно только при
что верно только при  При таких x множитель
При таких x множитель  Ясно, что при
Ясно, что при  то есть
то есть 
 при
при 
 и положительна при
и положительна при 
 то можно взять
то можно взять  то вторая скобка будет положительна при любом a. Итак, нужно чтобы
то вторая скобка будет положительна при любом a. Итак, нужно чтобы  Окончательно:
Окончательно: 

 положительно, при всех значениях
положительно, при всех значениях 



 где
где  Чтобы исходное неравенство выполнялось при любом значении x, необходимо и достаточно, чтобы выполнялось неравенство
Чтобы исходное неравенство выполнялось при любом значении x, необходимо и достаточно, чтобы выполнялось неравенство  где
где  — наибольшее значение функции
— наибольшее значение функции  Найдём это наибольшее значение.
Найдём это наибольшее значение.

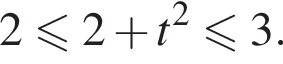

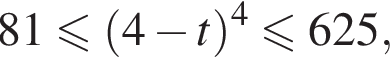

 то есть наибольшее значение числителя и наименьшее значение знаменателя достигается одновременно. Это означает, что
то есть наибольшее значение числителя и наименьшее значение знаменателя достигается одновременно. Это означает, что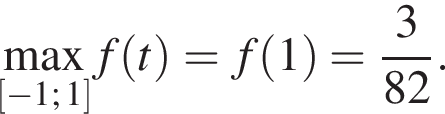
 исходное неравенство выполняется при любом значении x.
исходное неравенство выполняется при любом значении x.













 Получаем:
Получаем: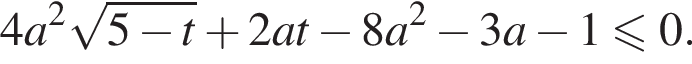
 тогда
тогда  Далее:
Далее:

 что верно. Поэтому
что верно. Поэтому 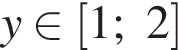 необходимо и достаточно, чтобы оно выполнялось при
необходимо и достаточно, чтобы оно выполнялось при  если
если 
 то достаточно проверять первые два условия.
то достаточно проверять первые два условия. 






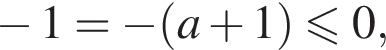

 то еще нужно, чтобы
то еще нужно, чтобы 





 и
и  Если хоть одно из неравенств строгое, то сумма квадратов меньше чем
Если хоть одно из неравенств строгое, то сумма квадратов меньше чем  и нужная точка найдена. Если же оба неравенства обращаются в равенства, то оба числа
и нужная точка найдена. Если же оба неравенства обращаются в равенства, то оба числа 



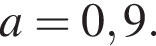





 и только их. Значит,
и только их. Значит,  (иначе неравенство не при всех x определено), то есть
(иначе неравенство не при всех x определено), то есть  Далее,
Далее,  и
и  (иначе основание логарифма будет неподходящим), поэтому
(иначе основание логарифма будет неподходящим), поэтому  и
и  Заменим теперь
Заменим теперь  на t и рационализируем неравенство:
на t и рационализируем неравенство:



 Разберем случаи.
Разберем случаи. то знаменатель отрицателен, а числитель положителен при всех допустимых t.
то знаменатель отрицателен, а числитель положителен при всех допустимых t. то
то  поэтому в одной из точек отрезка числитель будет равен 0.
поэтому в одной из точек отрезка числитель будет равен 0. то знаменатель положителен, а числитель отрицателен при всех допустимых t.
то знаменатель положителен, а числитель отрицателен при всех допустимых t.





 — неравенство верно всегда. Если
— неравенство верно всегда. Если 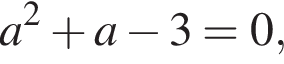 то получаем линейную непостоянную функцию
то получаем линейную непостоянную функцию  которая не может быть всюду положительна.
которая не может быть всюду положительна. то получается квадратное неравенство. Для того, чтобы оно было всегда выполнено при
то получается квадратное неравенство. Для того, чтобы оно было всегда выполнено при 


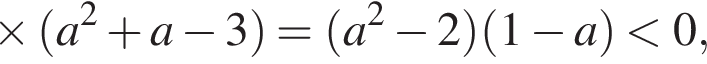
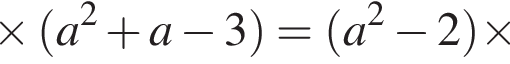

 Корни уравнения
Корни уравнения  это
это  Сравним числа
Сравним числа  и
и 
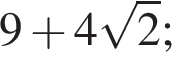

 Первое неравенство поэтому дает
Первое неравенство поэтому дает 



 корни у уравнения есть, но они неположительны. Тогда нужно потребовать, чтобы:
корни у уравнения есть, но они неположительны. Тогда нужно потребовать, чтобы: 


 Второе оставляет от первого промежутка лишь
Второе оставляет от первого промежутка лишь  которое подходит во все неравенства. Первое превращается для
которое подходит во все неравенства. Первое превращается для  в
в  что противоречит условию про положительность старшего коэффициента. Для
что противоречит условию про положительность старшего коэффициента. Для 


 значения больше 2?
значения больше 2? На всем этом отрезке функция
На всем этом отрезке функция 










 то есть при
то есть при  еще требуется:
еще требуется: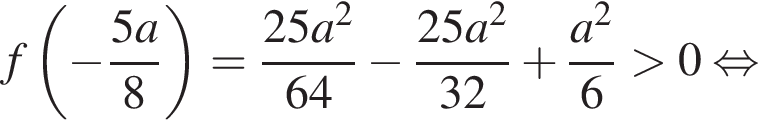



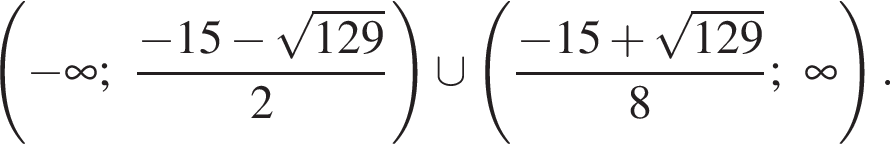

 неравенство принимает вид:
неравенство принимает вид:

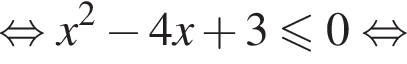

 можно взять
можно взять  и оно подойдет. Брать бОльшие x нельзя по условию — нас интересует лишь отрезок
и оно подойдет. Брать бОльшие x нельзя по условию — нас интересует лишь отрезок  неравенство принимает вид:
неравенство принимает вид:



 достигается при самом большом возможном x, то есть при
достигается при самом большом возможном x, то есть при 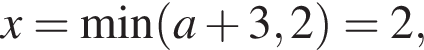 поскольку
поскольку  то есть
то есть 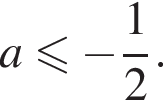 И действительно, при
И действительно, при  выполнено неравенство
выполнено неравенство  поэтому взять такое x можно.
поэтому взять такое x можно.
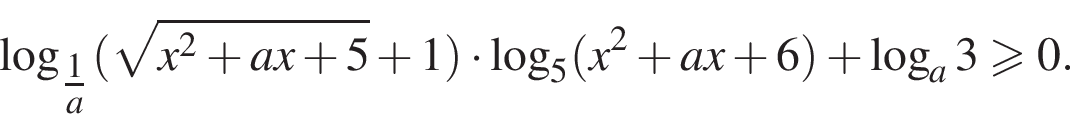


 тогда неравенство примет вид
тогда неравенство примет вид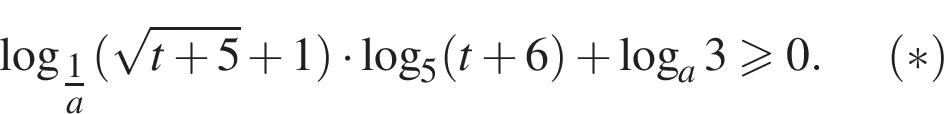


 в координатах
в координатах  то каждому значению переменной t соответствуют ровно два значения переменной x, значению
то каждому значению переменной t соответствуют ровно два значения переменной x, значению  соответствуют ровно одно значение x, значениям
соответствуют ровно одно значение x, значениям  не соответствуют никакие значения переменной x.
не соответствуют никакие значения переменной x.








 при
при 
 и не должно иметь решений
и не должно иметь решений 
 при
при 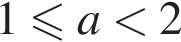 исходное неравенство решений не имеет.
исходное неравенство решений не имеет.


 тогда неравенство примет вид:
тогда неравенство примет вид:

 — возрастающая, как произведение двух неотрицательных возрастающих функций. Следовательно,неравенство (*) равносильно
— возрастающая, как произведение двух неотрицательных возрастающих функций. Следовательно,неравенство (*) равносильно  Тогда
Тогда
 если
если  т. е.
т. е.  Тогда
Тогда 
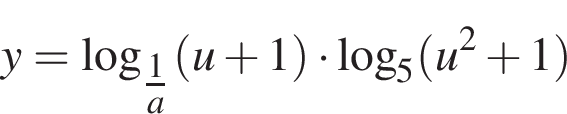 — возрастающая, как произведение двух неотрицательных возрастающих функций. Следовательно, неравенство (**) равносильно
— возрастающая, как произведение двух неотрицательных возрастающих функций. Следовательно, неравенство (**) равносильно  Тогда
Тогда





 — отрезок
— отрезок  на нём
на нём  имеет конечное число решений на
имеет конечное число решений на 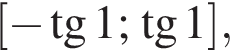 где
где  Преобразуем неравенство:
Преобразуем неравенство:


 при
при  которое входит в
которое входит в  Найдём соответствующие значения x:
Найдём соответствующие значения x: 
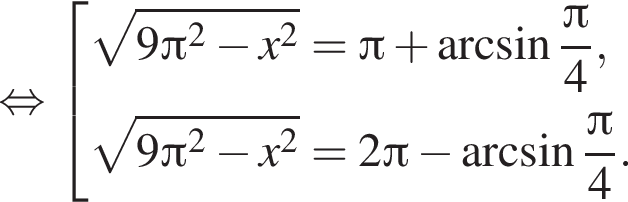
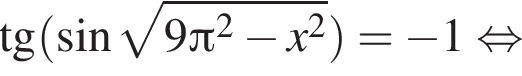



 или
или 
 имело конечное число точек, необходимо и достаточно, чтобы выполнялись условия
имело конечное число точек, необходимо и достаточно, чтобы выполнялись условия
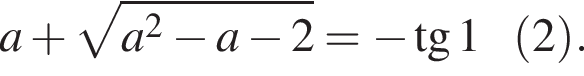


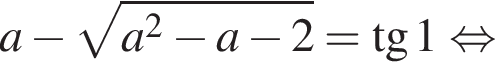










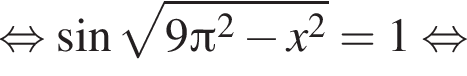
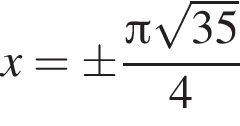 и
и 

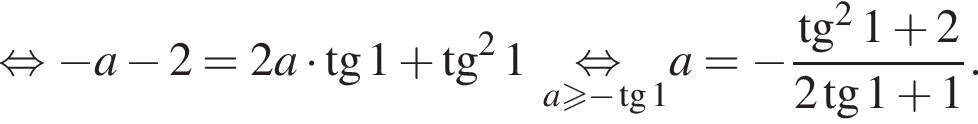




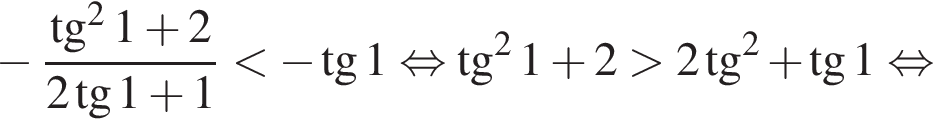

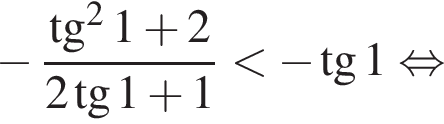


 при
при 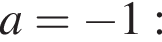

 выполняется неравенство
выполняется неравенство 
 поскольку иначе при
поскольку иначе при  так как иначе нельзя взять
так как иначе нельзя взять 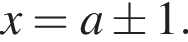 Далее, поскольку
Далее, поскольку  должно быть положительно на всем промежутке, то
должно быть положительно на всем промежутке, то 




 Учитывая ограничения из ОДЗ, получаем ответ
Учитывая ограничения из ОДЗ, получаем ответ 
