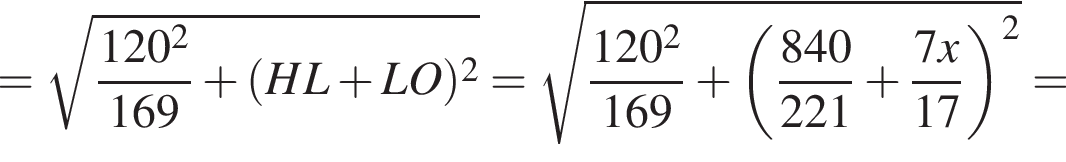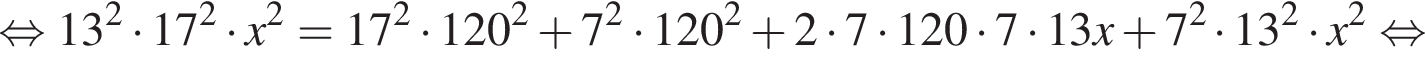В окружность вписан четырехугольник ABCD, диагонали которого взаимно перпендикулярны и пересекаются в точке E. Прямая, проходящая через точку E и перпендикулярная к AB, пересекает сторону CD в точке M. Известно, что AD = 8, AB = 4, угол CDB равен 60 градусов.
а) Докажите, что EM — медиана треугольника CED.
б) Найдите длину EM.
Решение. а) Углы ∠BDC и ∠BAC равны, так как они опираются на одну и ту же дугу BC. Тогда в ΔABE угол ∠ABE = 30° (так как ∠BAC = 60°). Обозначим точку пересечения прямой ME со стороной AB за K. Тогда в прямоугольном треугольнике BKE угол ∠BEK = 60°. Далее, ∠BEK = ∠MED = 60° (как вертикальные). Отсюда получаем, что ΔEDM — равносторонний (так как все углы по 60°), то есть EM = ED = MD ~ x. Так как в прямоугольном треугольнике CED против угла в 30° лежит катет, в 2 раза меньший гипотенузы, то CD = 2x. Получили, что так как DM = x, точка M является серединой гипотенузы CD, то есть EM — медиана ΔCED. Что и требовалось доказать.
б) Из ΔABE получаем, что  Тогда по теореме Пифагора из ΔADE получаем:
Тогда по теореме Пифагора из ΔADE получаем:


Ответ: ![]()
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б. | 3 |
| Получен обоснованный ответ в пункте б. ИЛИ Имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. | 2 |
| Имеется верное доказательство утверждения пункта а. ИЛИ При обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. ИЛИ Обоснованно получен верный ответ в пункте б и использованием утверждения пункта а, при этом пункт а не выполнен. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 3 |
 Величина угла АВМ равна 60 градусам, BM = 8.
Величина угла АВМ равна 60 градусам, BM = 8. тогда
тогда  (рис. 1).
(рис. 1).



 Так как
Так как 





 (Рис. 2).
(Рис. 2).






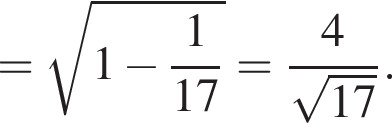














 где
где  по теореме Пифагорa получим:
по теореме Пифагорa получим: 
 аналогично
аналогично 

 б) 17.
б) 17. ), то есть получается, что BO — гипотенуза и диаметр малой окружности с центром в точке E. Далее, треугольник BTO вписан в малую окружность, а его угол BTO опирается на диаметр, и потому равен
), то есть получается, что BO — гипотенуза и диаметр малой окружности с центром в точке E. Далее, треугольник BTO вписан в малую окружность, а его угол BTO опирается на диаметр, и потому равен  и O является центром окружности, описанной вокруг треугольника ABC, то OT — серединный перпендикуляр, то есть T — середина AB. Значит, TR — средняя линия треугольника ABC, поэтому TR || AC.
и O является центром окружности, описанной вокруг треугольника ABC, то OT — серединный перпендикуляр, то есть T — середина AB. Значит, TR — средняя линия треугольника ABC, поэтому TR || AC.  (как соответственные при параллельных прямых). В итоге получаем:
(как соответственные при параллельных прямых). В итоге получаем:


 — равносторонний (так как все углы по
— равносторонний (так как все углы по  Тогда по теореме Пифагора из ΔADE получаем:
Тогда по теореме Пифагора из ΔADE получаем:
 откуда
откуда  Тогда
Тогда




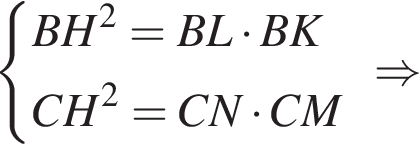

 откуда
откуда  Выразим различными способами площадь треугольника ABC.
Выразим различными способами площадь треугольника ABC.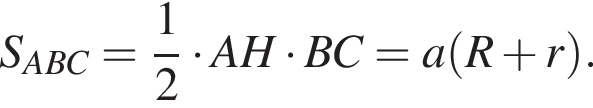


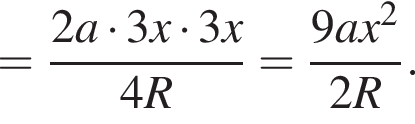









 ), получим:
), получим: 



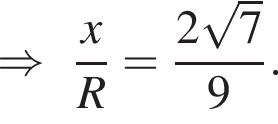

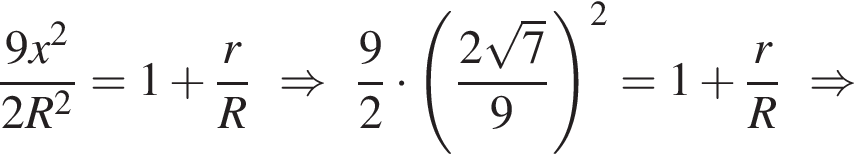



 Известно, что в четырехугольник можно вписать окружность в том и только в том случае, если суммы противолежащих сторон этого четырехугольника равны. Следовательно, MN + BC = AM + CN. Поскольку по условию задачи MN — средняя линия треугольника АВС, то
Известно, что в четырехугольник можно вписать окружность в том и только в том случае, если суммы противолежащих сторон этого четырехугольника равны. Следовательно, MN + BC = AM + CN. Поскольку по условию задачи MN — средняя линия треугольника АВС, то  Тогда ВM + CN = BC + MN = 9,5 + 4,75 = 14,25. В таком случае также будет выполнено условия: АМ + АN = 14,25, АВ + АС = 2 · 14,25 = 28,5.
Тогда ВM + CN = BC + MN = 9,5 + 4,75 = 14,25. В таком случае также будет выполнено условия: АМ + АN = 14,25, АВ + АС = 2 · 14,25 = 28,5.
 В
В 


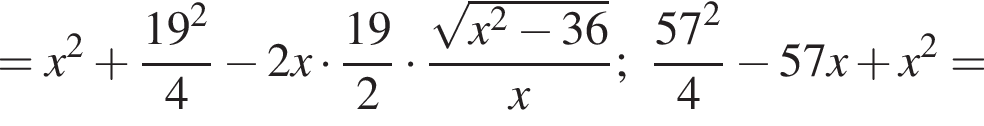




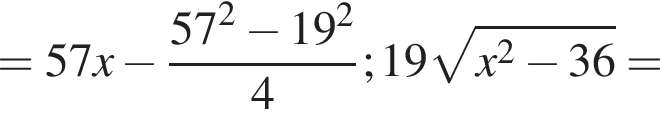













 (не подходит, так как 28,5 − 18,5 = 10, в таком случае 18,5 не есть дина меньшей из боковых сторон).
(не подходит, так как 28,5 − 18,5 = 10, в таком случае 18,5 не есть дина меньшей из боковых сторон).

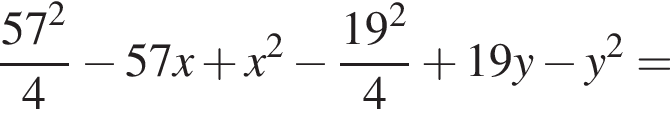
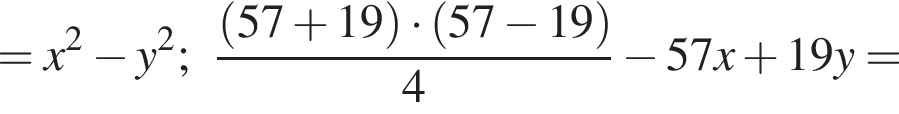





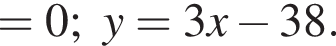




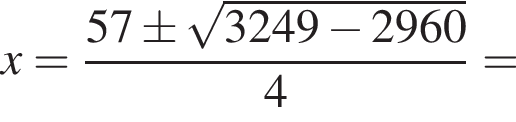

 что и требовалось доказать.
что и требовалось доказать.









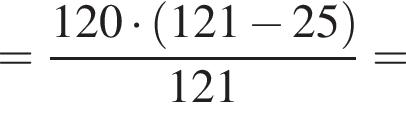

 Откуда:
Откуда:



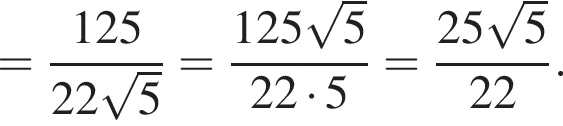

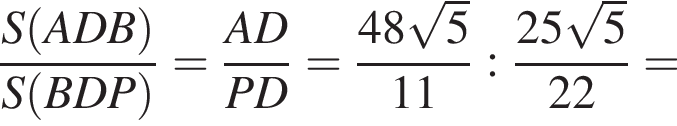


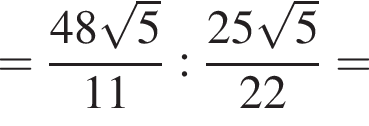


 то:
то:




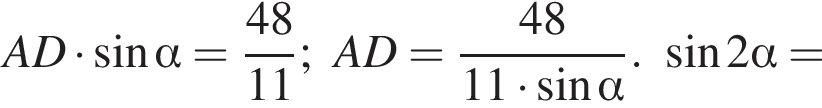











 (как вписанные углы, опирающиеся на одну дугу), а
(как вписанные углы, опирающиеся на одну дугу), а  как углы равнобедренного треугольника ADC, то
как углы равнобедренного треугольника ADC, то  Кроме того, у треугольников ABC и AEC есть общий угол C, поэтому они подобны по двум углам.
Кроме того, у треугольников ABC и AEC есть общий угол C, поэтому они подобны по двум углам. то есть
то есть  откуда
откуда  и
и 
 (опираются на дугу BC),
(опираются на дугу BC), 
 то есть треугольник DEM равнобедренный. Далее
то есть треугольник DEM равнобедренный. Далее 
 значит, EM — медиана CDE.
значит, EM — медиана CDE. и поэтому в треугольнике EAB имеем
и поэтому в треугольнике EAB имеем  Тогда
Тогда 
 за
за 

 C другой стороны, в описанной окружности треугольника KMH это центральный угол, опирающийся на ту же дугу, что и вписанный угол KHM. Значит,
C другой стороны, в описанной окружности треугольника KMH это центральный угол, опирающийся на ту же дугу, что и вписанный угол KHM. Значит,  откуда
откуда 
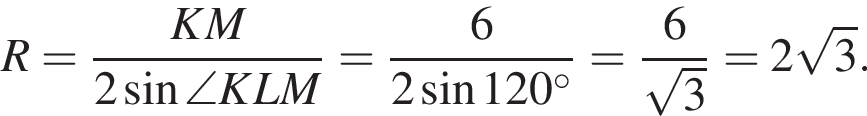




 Тогда
Тогда 








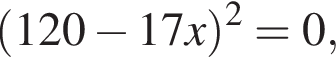






 По усиленной теореме синусов в треугольнике ABC имеем
По усиленной теореме синусов в треугольнике ABC имеем  откуда
откуда  и
и 

 Рассмотрим три случая.
Рассмотрим три случая. 
 Отсюда
Отсюда 

 Отсюда
Отсюда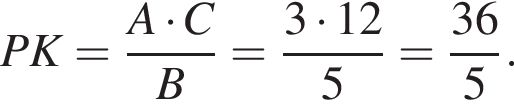
 Получаем:
Получаем:

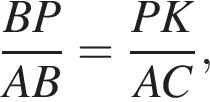








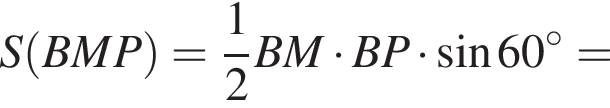




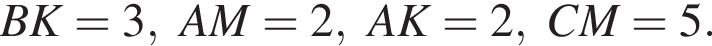
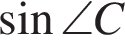 по теореме синусов.
по теореме синусов.



















 В треугольник вписана окружность, которая касается сторон AC, CB, BA в точках K, T и M соответственно. Прямая AT пересекает окружность в точке L, причем AL = 2. Найдите площадь треугольника, одна из сторон которого AT, а другая содержит точку касания окружностью треугольника АВС, если AK = 4.
В треугольник вписана окружность, которая касается сторон AC, CB, BA в точках K, T и M соответственно. Прямая AT пересекает окружность в точке L, причем AL = 2. Найдите площадь треугольника, одна из сторон которого AT, а другая содержит точку касания окружностью треугольника АВС, если AK = 4.

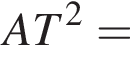





 не подходит по смыслу задачи.
не подходит по смыслу задачи. 








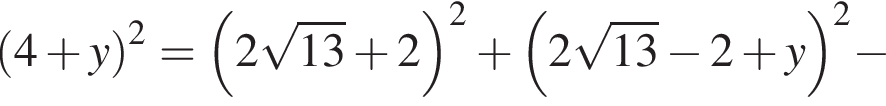







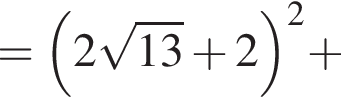



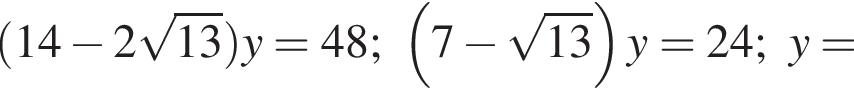









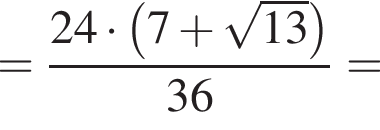

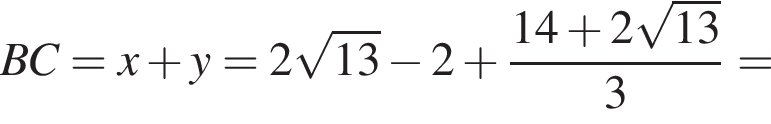


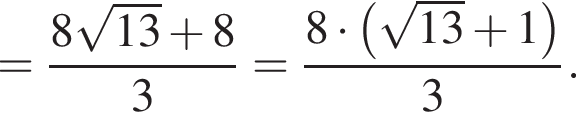










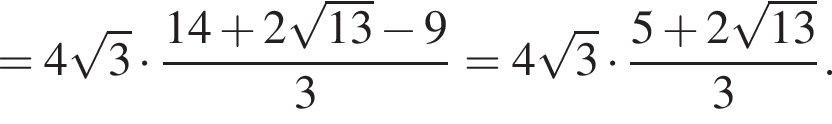
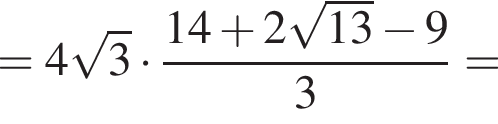
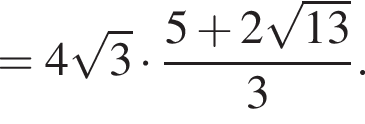






 и
и 
 а все отрезки на сторонах равны
а все отрезки на сторонах равны 
 а перпендикуляры на меньший катет падают на расстояниях 2 и
а перпендикуляры на меньший катет падают на расстояниях 2 и 
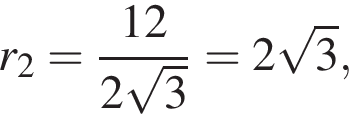 а перпендикуляры на меньший катет падают на расстояниях 2 и 6 от вершины прямого угла, и расстояние между ними будет 4.
а перпендикуляры на меньший катет падают на расстояниях 2 и 6 от вершины прямого угла, и расстояние между ними будет 4. 
 а перпендикуляры на меньший катет падают на расстояниях 3 и
а перпендикуляры на меньший катет падают на расстояниях 3 и 


 и
и  (вписанные углы, опирающиеся на одну дугу), треугольники LKF и MNF подобны с коэффициентом
(вписанные углы, опирающиеся на одну дугу), треугольники LKF и MNF подобны с коэффициентом  Пусть
Пусть 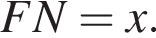 Тогда
Тогда 









 откуда
откуда 

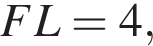 и все вычисления дают радиус окружности, описанной треугольника около FLM, который подобен треугольнику KFN с коэффициентом
и все вычисления дают радиус окружности, описанной треугольника около FLM, который подобен треугольнику KFN с коэффициентом  Тогда треугольники
Тогда треугольники  и углу между ними. Равенство углов следует из равенства дуг
и углу между ними. Равенство углов следует из равенства дуг 
 стягиваемых равными хордами. Тогда равны дуги
стягиваемых равными хордами. Тогда равны дуги  и
и 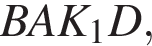 а значит, равны и опирающиеся на них вписанные углы.
а значит, равны и опирающиеся на них вписанные углы. При этом точка
При этом точка  Значит, точка
Значит, точка 

 где l — длина хорды, в нашем случае l = АС = 12.
где l — длина хорды, в нашем случае l = АС = 12. 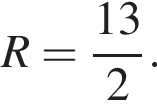



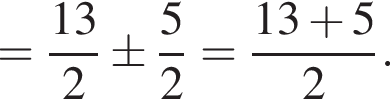

 Итак, АС и диаметр окружности S — две хорды этой же окружности, пересекающиеся в точке D. Для них выполнимо:
Итак, АС и диаметр окружности S — две хорды этой же окружности, пересекающиеся в точке D. Для них выполнимо:  или
или 










 в точке M и основание
в точке M и основание  в точке N. Обозначим также центр окружности за O, а точку пересечения диагоналей за T. Имеем тогда
в точке N. Обозначим также центр окружности за O, а точку пересечения диагоналей за T. Имеем тогда




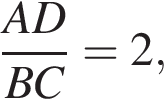 поэтому и их высоты из точки T относятся также, откуда
поэтому и их высоты из точки T относятся также, откуда  Наконец,
Наконец, 


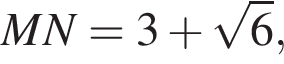 соответственно
соответственно  то есть точка T лежит с той же стороны от центра, что и меньшее основание трапеции, поэтому
то есть точка T лежит с той же стороны от центра, что и меньшее основание трапеции, поэтому 

 тогда
тогда 














 (равные хорды стягивают равные дуги, углы опирающиеся на равные дуги, равны), откуда ABCD — равнобедренная трапеция. Ее высота равна
(равные хорды стягивают равные дуги, углы опирающиеся на равные дуги, равны), откуда ABCD — равнобедренная трапеция. Ее высота равна  Искомая окружность тогда — описанная окружность треугольника DAC. Найдем ее радиус по формуле
Искомая окружность тогда — описанная окружность треугольника DAC. Найдем ее радиус по формуле

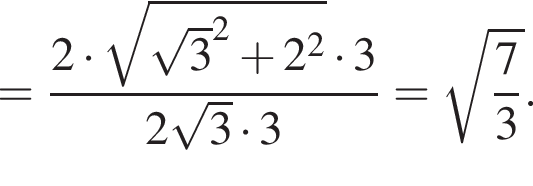
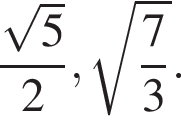




 ), рисунок слева (для экономии места изображена часть окружности). Тупой вписанный угол, опирающийся на дугу AC, находится как разность
), рисунок слева (для экономии места изображена часть окружности). Тупой вписанный угол, опирающийся на дугу AC, находится как разность  Далее аналогично первому случаю: из треугольника ABC получаем:
Далее аналогично первому случаю: из треугольника ABC получаем:  Из треугольника AMC получим:
Из треугольника AMC получим:

 в противном случае
в противном случае 
 а это противоречит условию.
а это противоречит условию.

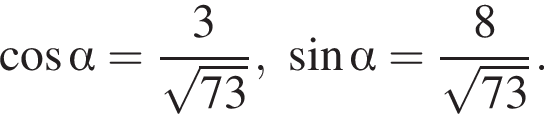




 то
то 








 Точка Р совпадет с точками пресечения окружности с осью ординат.
Точка Р совпадет с точками пресечения окружности с осью ординат. Найдем абсциссы точки Р.
Найдем абсциссы точки Р. 

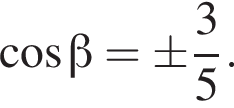 Так как абсцисса точки Р будет равна
Так как абсцисса точки Р будет равна  то искомое расстояние либо равно
то искомое расстояние либо равно  (не подходит), либо
(не подходит), либо  (удовлетворяет условию задачи).
(удовлетворяет условию задачи). поскольку они оба равны
поскольку они оба равны  — один как накрест лежащий, второй — как угол при биссектрисе.
— один как накрест лежащий, второй — как угол при биссектрисе. как касательные к вписанной окружности треугольника ABE. Тогда треугольники BMH и BAE подобны (
как касательные к вписанной окружности треугольника ABE. Тогда треугольники BMH и BAE подобны ( ) и
) и  откуда
откуда 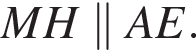
 тогда коэффициент подобия треугольников BMH и BAE равен
тогда коэффициент подобия треугольников BMH и BAE равен 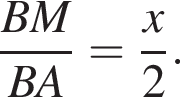 Тогда
Тогда 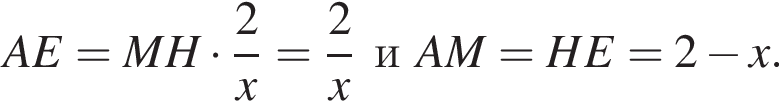
 то есть
то есть  откуда
откуда 
 У него две противолежащие стороны
У него две противолежащие стороны  по построению, то
по построению, то  Значит,
Значит,  — параллелограмм по признаку параллелограмма.
— параллелограмм по признаку параллелограмма.  этого параллелограмма прямой по построению, значит,
этого параллелограмма прямой по построению, значит,  А это значит, что прямая
А это значит, что прямая  см. рис.)
см. рис.) 
 как внутренние накрест лежащие при параллельных прямых AB, DC и секущей AF. Значит,
как внутренние накрест лежащие при параллельных прямых AB, DC и секущей AF. Значит,  Отсюда:
Отсюда: 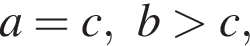
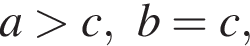

 не выполняется неравенство b > c.
не выполняется неравенство b > c. не выполняется неравенство a > c.
не выполняется неравенство a > c. то
то  не выполняется равенство (*). Следовательно, равенство (*) будет иметь место только при выполнении равенства a = b = c.
не выполняется равенство (*). Следовательно, равенство (*) будет иметь место только при выполнении равенства a = b = c. 








 Выпишем теорему косинусов для треугольника ABC:
Выпишем теорему косинусов для треугольника ABC:









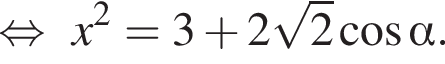









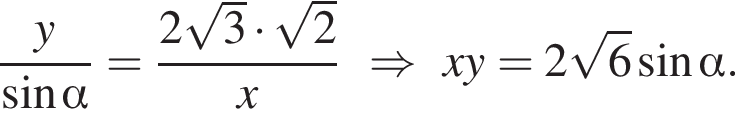
 в самое первое выражение теоремы косинусов:
в самое первое выражение теоремы косинусов:


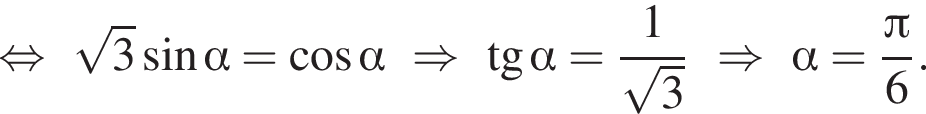




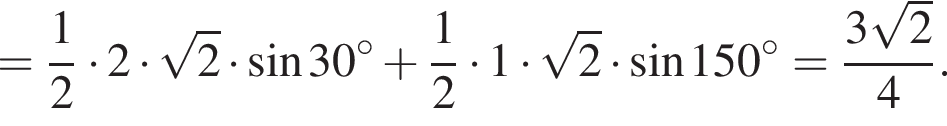

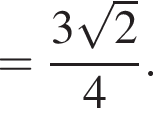


 отсюда:
отсюда: 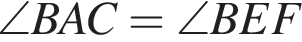 как углы, заключенные между взаимно перпендикулярными прямыми. (2)
как углы, заключенные между взаимно перпендикулярными прямыми. (2) как вертикальные углы. (3)
как вертикальные углы. (3)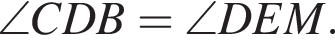 Отсюда: DM = EM. Аналогично можно доказать, что CM = EM. Следовательно, EM — медиана треугольника CЕD.
Отсюда: DM = EM. Аналогично можно доказать, что CM = EM. Следовательно, EM — медиана треугольника CЕD.
 в котором
в котором  по теореме Пифагора:
по теореме Пифагора: 


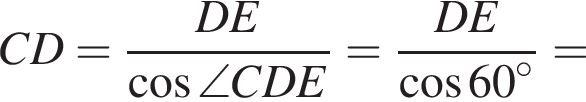



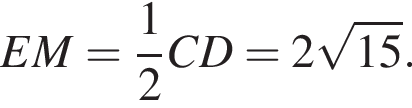
 опирающимся на ее диаметр ВС, т. е.
опирающимся на ее диаметр ВС, т. е.  что и требовалось доказать.
что и требовалось доказать.  (Здесь радиусы окружностей
(Здесь радиусы окружностей 

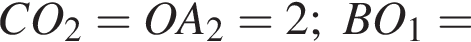




 — прямоугольник,
— прямоугольник, 
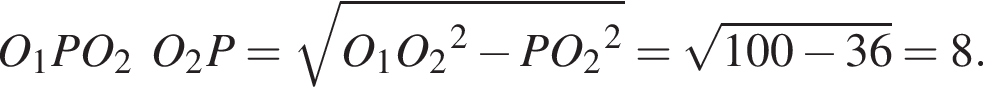

 (СК есть высота
(СК есть высота  проведенная к продолжению стороны
проведенная к продолжению стороны  (Отрезок ВК равен высоте
(Отрезок ВК равен высоте  проведенной к
проведенной к 



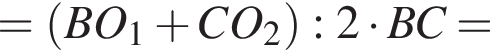



 а радиус окружности равен
а радиус окружности равен  Пусть
Пусть 
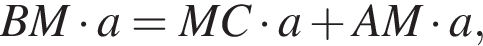 т. е. BM = MC + AM, что и требовалось доказать.
т. е. BM = MC + AM, что и требовалось доказать. — это с одной стороны, а с другой же стороны
— это с одной стороны, а с другой же стороны 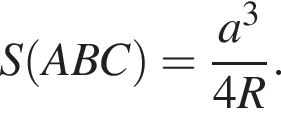


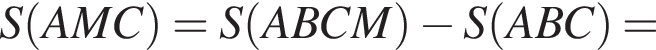







 по теореме косинусов:
по теореме косинусов:







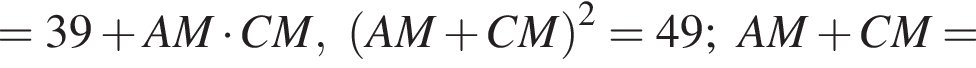




 MN и CD — не параллельны, четырехугольник NMDC — трапеция. Однако, любая трапеция, вписанная в окружность, непременно является равнобедренной. А у равнобедренной трапеции диагонали равны.
MN и CD — не параллельны, четырехугольник NMDC — трапеция. Однако, любая трапеция, вписанная в окружность, непременно является равнобедренной. А у равнобедренной трапеции диагонали равны. 






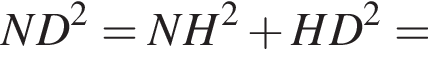




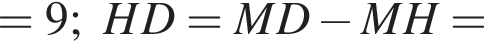






 и DX = 6.
и DX = 6.
 Тогда
Тогда 
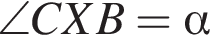 (накрест лежащий с
(накрест лежащий с  ),
),  (накрест лежащий с
(накрест лежащий с 

 (поскольку точки лежат на окружности), и поэтому
(поскольку точки лежат на окружности), и поэтому  Тогда
Тогда 
 (из подобия треугольников ABX и BXC).
(из подобия треугольников ABX и BXC). (из подобия треугольников BXC и XCD).
(из подобия треугольников BXC и XCD).




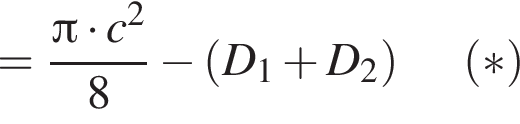






 значит,
значит,  (**)
(**) что и требовалось доказать.
что и требовалось доказать. 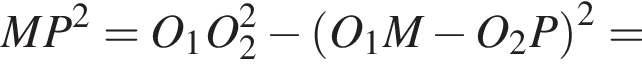












 что и требовалось доказать.
что и требовалось доказать. 
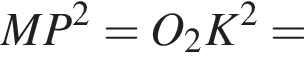




 или AD · BP = BC · DP, что и требовалось доказать.
или AD · BP = BC · DP, что и требовалось доказать.

 т. е.
т. е. 



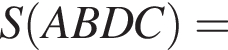












 что и требовалось доказать.
что и требовалось доказать.




 Тогда
Тогда  с одной стороны,
с одной стороны,  — со стороны другой. Следовательно,
— со стороны другой. Следовательно, 
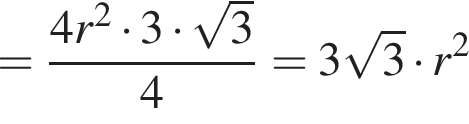












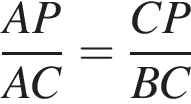 или BC : AC = CP : AP, что и требовалось доказать.
или BC : AC = CP : AP, что и требовалось доказать. По доказанному выше:
По доказанному выше:  значит,
значит,
 Следовательно,
Следовательно, 





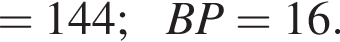
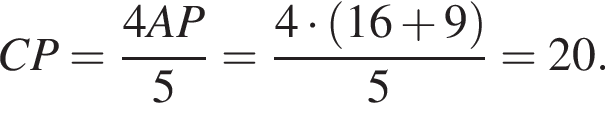
 проведены медианы АМ и ВК. Известно, что около четырехугольника АВМК можно описать окружность.
проведены медианы АМ и ВК. Известно, что около четырехугольника АВМК можно описать окружность. Так как по условию
Так как по условию 
 то
то  откуда
откуда  что и требовалось доказать.
что и требовалось доказать. где
где 

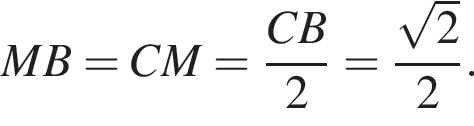

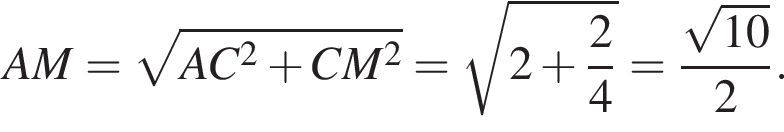



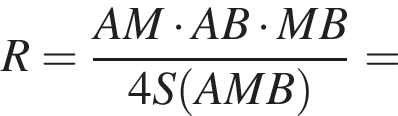

 то есть ABMK — вписанная трапеция. Значит, она равнобедренная, то есть
то есть ABMK — вписанная трапеция. Значит, она равнобедренная, то есть  Тогда и
Тогда и 
 тогда
тогда 
 и
и 

 точки касания окружностей:
точки касания окружностей:  общую точку AC и окр.
общую точку AC и окр.  Он равносторонний, поскольку каждая его сторона равна
Он равносторонний, поскольку каждая его сторона равна  следовательно, каждая его сторона будет равна r, что и требовалось доказать.
следовательно, каждая его сторона будет равна r, что и требовалось доказать.  а это значит, что
а это значит, что 



















 то есть
то есть 










 площадь ромба
площадь ромба  Надо показать следующее:
Надо показать следующее:
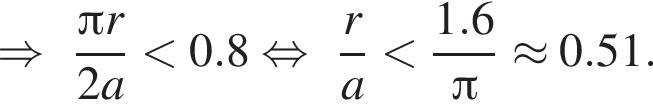
 Значит, во всех остальных случаях высота OH будет только меньше, чем 0.5. Таким образом, доказали, что
Значит, во всех остальных случаях высота OH будет только меньше, чем 0.5. Таким образом, доказали, что 
 и из прямоугольного треугольника BOC найдем:
и из прямоугольного треугольника BOC найдем: 


 обозначим
обозначим  откуда получим по основному тригонометрическому тождеству:
откуда получим по основному тригонометрическому тождеству:

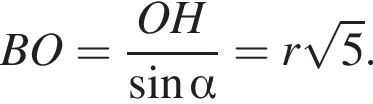
 Из прямоугольного треугольника
Из прямоугольного треугольника 
















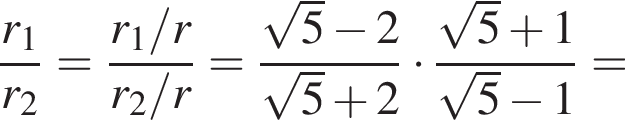







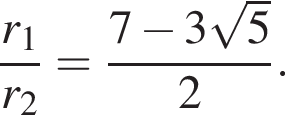

 Можно заметить, что
Можно заметить, что  — это парабола с ветвями, направленными вниз. Тогда вершина параболы находится по формуле
— это парабола с ветвями, направленными вниз. Тогда вершина параболы находится по формуле 















 Тогда:
Тогда:
 Если OD = t, то AO = 2t. А также:
Если OD = t, то AO = 2t. А также: 




 Таким образом,
Таким образом, 

































 Тогда по теореме Пифагора находим
Тогда по теореме Пифагора находим  Значит,
Значит, 
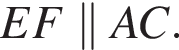 Рассматривая аналогично остальные стороны EFGH, получаем, что это параллелограмм и даже прямоугольник (так как
Рассматривая аналогично остальные стороны EFGH, получаем, что это параллелограмм и даже прямоугольник (так как  ). Значит, его площадь равна:
). Значит, его площадь равна:

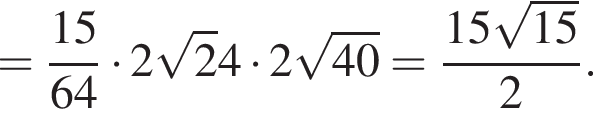

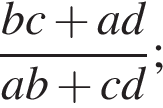








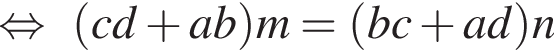

 тогда
тогда 




























 откуда искомая высота равна
откуда искомая высота равна 
 то равны и дуги AB и CD, а значит и опирающиеся на них углы
то равны и дуги AB и CD, а значит и опирающиеся на них углы  Поэтому накрест лежащие углы, образованные сторонами BC и AD с секущей BD, равны. Поэтому ABCD — трапеция. Ее боковые стороны равны по условию.
Поэтому накрест лежащие углы, образованные сторонами BC и AD с секущей BD, равны. Поэтому ABCD — трапеция. Ее боковые стороны равны по условию. Опустим перпендикуляры BE и CF на сторону AD. Тогда
Опустим перпендикуляры BE и CF на сторону AD. Тогда  аналогично
аналогично  поэтому
поэтому 
 тогда
тогда 
 и
и 















 (по теореме о пересекающихся хордах). Тогда высота равнобедренного треугольника CDK равна
(по теореме о пересекающихся хордах). Тогда высота равнобедренного треугольника CDK равна 







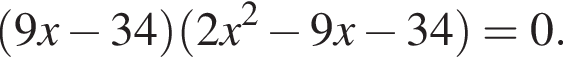
 или
или 
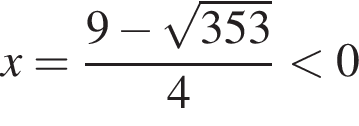 и
и 





 Тогда
Тогда 
 значит,
значит,


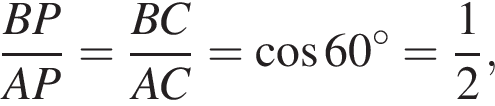 значит,
значит,  Поэтому
Поэтому
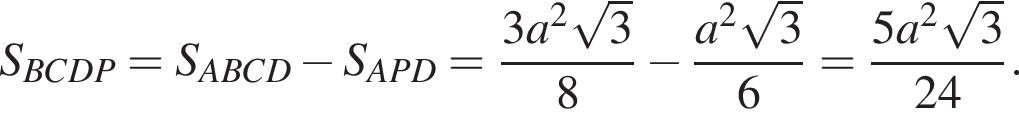

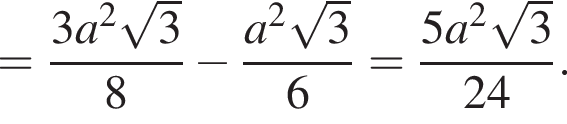


 Опустим высоты BE и CF на основание AD. Тогда
Опустим высоты BE и CF на основание AD. Тогда  Поскольку трапеция описанная и равнобедренная, то
Поскольку трапеция описанная и равнобедренная, то 
 Очевидно, что диаметр окружности равен расстоянию между основаниями трапеции, то есть как раз найденной высоте.
Очевидно, что диаметр окружности равен расстоянию между основаниями трапеции, то есть как раз найденной высоте. а радиус, следовательно, равен 6. Боковая сторона трапеции равна 13. Поскольку верхнее основание поделено точкой касания на отрезки длиной 4, а нижнее — на отрезки длиной 9, боковая сторона поделена на отрезки длиной 4 и 9.
а радиус, следовательно, равен 6. Боковая сторона трапеции равна 13. Поскольку верхнее основание поделено точкой касания на отрезки длиной 4, а нижнее — на отрезки длиной 9, боковая сторона поделена на отрезки длиной 4 и 9.


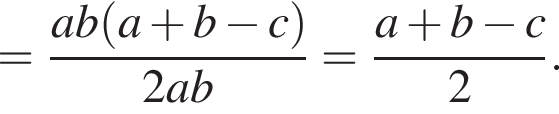


 Как известно, треугольники ABD и BCD подобны с коэффициентом
Как известно, треугольники ABD и BCD подобны с коэффициентом  Тогда
Тогда 
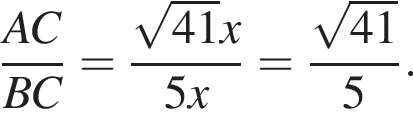

 Тогда если r — радиус вписанной окружности и
Тогда если r — радиус вписанной окружности и  Вычислим площадь треугольника ABC двумя способами:
Вычислим площадь треугольника ABC двумя способами:






 Найдем радиус вписанной окружности.
Найдем радиус вписанной окружности. 

 Заметим также, что
Заметим также, что 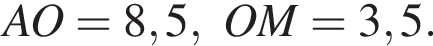
 тогда
тогда 
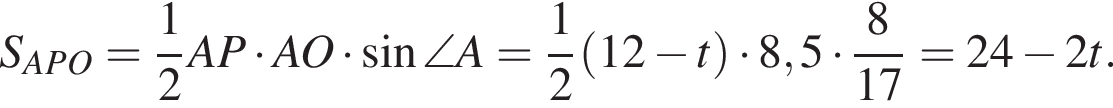


 Поскольку
Поскольку  а
а  по теореме Пифагора для треугольника ABC имеем
по теореме Пифагора для треугольника ABC имеем




 (поскольку центр описанной окружности — середина гипотенузы). Тогда прямая OP, проходящая через нее, имеет уравнение
(поскольку центр описанной окружности — середина гипотенузы). Тогда прямая OP, проходящая через нее, имеет уравнение 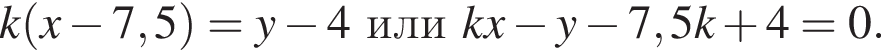







 дает прямую AB).
дает прямую AB). Значит, координаты точки P —
Значит, координаты точки P — 

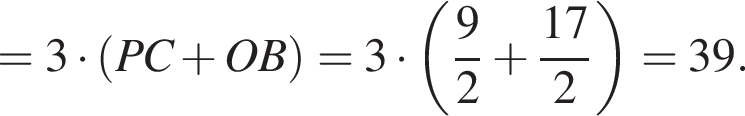




 точки M, A и B лежат на одной прямой, значит, отрезок CM — высота треугольника ABC (см. рис.).
точки M, A и B лежат на одной прямой, значит, отрезок CM — высота треугольника ABC (см. рис.).









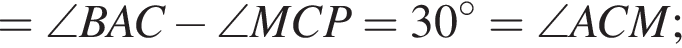


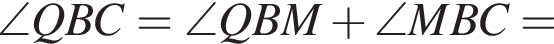




 как хорды стягивающие равные дуги. Таким образом,
как хорды стягивающие равные дуги. Таким образом, 




 (из вписанности), откуда
(из вписанности), откуда  и ABCD — ромб.
и ABCD — ромб.
 Опустим также перпендикуляры HE и HF на AO и BO. Тогда прямоугольник EHFO по площади ровно в 4 раза меньше, чем требуемый четырехугольник (он состоит из четырех таких прямоугольников). Тогда
Опустим также перпендикуляры HE и HF на AO и BO. Тогда прямоугольник EHFO по площади ровно в 4 раза меньше, чем требуемый четырехугольник (он состоит из четырех таких прямоугольников). Тогда






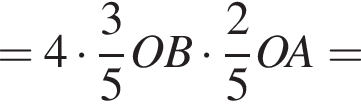


 и ВС = 15.
и ВС = 15. Тогда
Тогда  поскольку
поскольку  тогда
тогда  и
и  по теореме о вписанном угле. Аналогично
по теореме о вписанном угле. Аналогично 



 По признаку вписанноти чеырехугольника BMCO — вписанный. Центр его описанной окружности и есть искомая точка.
По признаку вписанноти чеырехугольника BMCO — вписанный. Центр его описанной окружности и есть искомая точка. поэтому точка M лежит вне треугольника, порядок точек именно такой и признаком пользоваться можно).
поэтому точка M лежит вне треугольника, порядок точек именно такой и признаком пользоваться можно).









 Теперь применим теорему синусов
Теперь применим теорему синусов
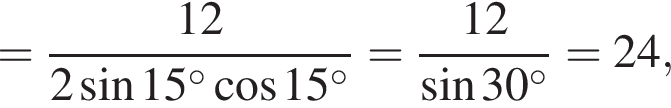

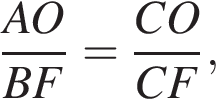 откуда
откуда






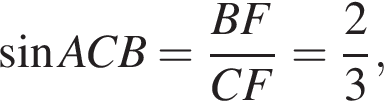
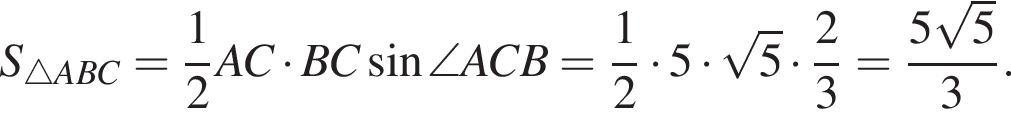
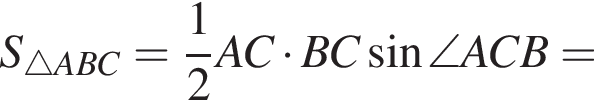

 Найдите расстояние от вершины В до прямой АС.
Найдите расстояние от вершины В до прямой АС. тогда
тогда  как угол между касательной и хордой. Тогда
как угол между касательной и хордой. Тогда 
 тогда по теореме косинусов имеем
тогда по теореме косинусов имеем 
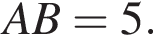

 и по свойству биссектрисы
и по свойству биссектрисы  откуда
откуда 
 находим
находим 
 на сторону AC и обозначим их
на сторону AC и обозначим их  соответственно. Тогда
соответственно. Тогда
 K — середина BC и
K — середина BC и 
 и
и 
 и
и 


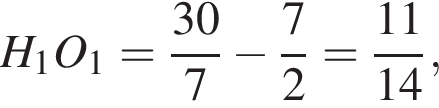

 мы знаем все стороны, кроме
мы знаем все стороны, кроме 





 BC = 9, AD = 18.
BC = 9, AD = 18.


 лежат на одной окружности. Но тогда
лежат на одной окружности. Но тогда 
 По свойству описанного четырехугольника
По свойству описанного четырехугольника  По теореме Пифагора для треугольника CHD находим
По теореме Пифагора для треугольника CHD находим  откуда
откуда 
 Далее, треугольники BEC и DEA подобны с коэффициентом
Далее, треугольники BEC и DEA подобны с коэффициентом 






 поскольку BD — диаметр окружности. Значит, в треугольнике CBD точка P — точка пересечения высот, поэтому
поскольку BD — диаметр окружности. Значит, в треугольнике CBD точка P — точка пересечения высот, поэтому  Тогда
Тогда 

 Пусть H - основание высоты из A на
Пусть H - основание высоты из A на 

 Тогда по свойству пересекающихся хорд
Тогда по свойству пересекающихся хорд  откуда
откуда 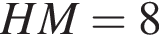 и
и  Далее,
Далее,  поэтому
поэтому  По теореме косинусов найдем
По теореме косинусов найдем





 а радиус окружности, вписанной в ромб, равен 1.
а радиус окружности, вписанной в ромб, равен 1.
 Тогда из прямоугольных треугольников EHC и EGA получаем
Тогда из прямоугольных треугольников EHC и EGA получаем 
 Поэтому:
Поэтому: 






 откуда
откуда 
 и
и 
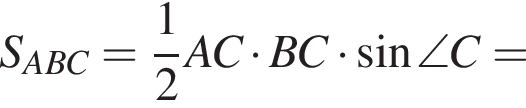


 и расстояние между центрами равно:
и расстояние между центрами равно:


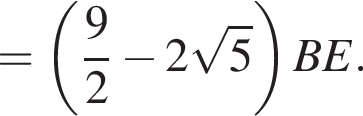



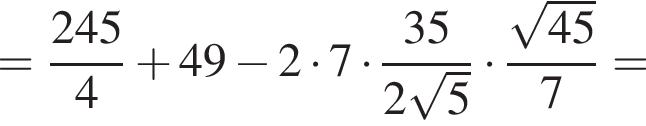






 откуда
откуда  тогда
тогда  или
или  Воспользуемся тем, что AD > BC. Если сдвигать точку A к точке D, точка M будет перемещаться по дуге в сторону точки D, таким образом, дуга NBM будет увеличиваться. В тот момент, когда основания станут равны, точки M и N станут симметричны относительно середины отрезка BD, то есть станут диаметрально противоположны. Итак, если увеличивать дугу NBM, то она станет полуокружностью, значит, на исходной картинке она меньше полуокружности, поэтому
Воспользуемся тем, что AD > BC. Если сдвигать точку A к точке D, точка M будет перемещаться по дуге в сторону точки D, таким образом, дуга NBM будет увеличиваться. В тот момент, когда основания станут равны, точки M и N станут симметричны относительно середины отрезка BD, то есть станут диаметрально противоположны. Итак, если увеличивать дугу NBM, то она станет полуокружностью, значит, на исходной картинке она меньше полуокружности, поэтому  Таким образом,
Таким образом,  Высота трапеции равна диаметру окружности:
Высота трапеции равна диаметру окружности:  Пусть длина верхнего основания трапеции равна а, а длина нижнего равна b, из выражения для площади трапеции находим, что:
Пусть длина верхнего основания трапеции равна а, а длина нижнего равна b, из выражения для площади трапеции находим, что: 
 а
а  В прямоугольном треугольнике CBD находим:
В прямоугольном треугольнике CBD находим:  В прямоугольном треугольнике ADB находим:
В прямоугольном треугольнике ADB находим:  Угол MDC, равный сумме углов CBD и ADB, опирается на ту же хорду, что и угол MBC, но его вершина лежит по другую сторону от этой хорды, поэтому
Угол MDC, равный сумме углов CBD и ADB, опирается на ту же хорду, что и угол MBC, но его вершина лежит по другую сторону от этой хорды, поэтому  Следовательно,
Следовательно, 



 Подставляя значения тангенсов, находим:
Подставляя значения тангенсов, находим:
 получаем:
получаем:





 и
и 
 тогда
тогда 
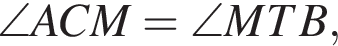 прямая AC параллельна прямой TB и
прямая AC параллельна прямой TB и  Кроме того
Кроме того  и
и  поэтому треугольники TBC и DCK равны по первому признаку. Значит,
поэтому треугольники TBC и DCK равны по первому признаку. Значит, 

 и
и 



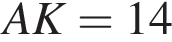 из такого же треугольника ACK.
из такого же треугольника ACK.
 а радиус окружности равен 13.
а радиус окружности равен 13. (первый — угол между касательной и хордой, второй — вписанный угол) и
(первый — угол между касательной и хордой, второй — вписанный угол) и  (вписанные, опирающиеся на одну дугу). Значит,
(вписанные, опирающиеся на одну дугу). Значит,


 поэтому треугольники подобны по двум углам.
поэтому треугольники подобны по двум углам.






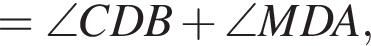
 Кроме того,
Кроме того,  из параллельности. Значит,
из параллельности. Значит,  поэтому BC — касательная к окружности. Тогда высота CH трапеции является частью диаметра окружности и, следовательно, проходит через середину хорды ND, откуда
поэтому BC — касательная к окружности. Тогда высота CH трапеции является частью диаметра окружности и, следовательно, проходит через середину хорды ND, откуда  Из теоремы синусов для треугольника CDN имеем
Из теоремы синусов для треугольника CDN имеем 





 откуда
откуда 
 то есть
то есть 















 Тогда
Тогда 











 а DC = 10.
а DC = 10. углы BDC и BCD равны. Углы EBC и DAC равны как вписанные углы. Угол EAD равен углу ABD как угол между касательной и хордой. Пусть
углы BDC и BCD равны. Углы EBC и DAC равны как вписанные углы. Угол EAD равен углу ABD как угол между касательной и хордой. Пусть  тогда:
тогда:































 и
и  Значит, треугольники FAK и HBK подобны по двум углам и треугольники KAH и KBE подобен по двум углам. Таким образом,
Значит, треугольники FAK и HBK подобны по двум углам и треугольники KAH и KBE подобен по двум углам. Таким образом,
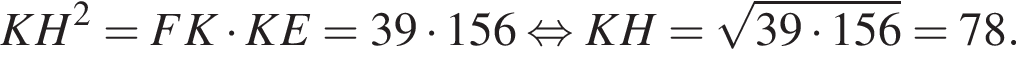



 Значит,
Значит,



 Пусть P и Q — проекции точек O и O1 соответственно на прямую BA1. Точка P — середина BE, точка Q — середина A1E, тогда
Пусть P и Q — проекции точек O и O1 соответственно на прямую BA1. Точка P — середина BE, точка Q — середина A1E, тогда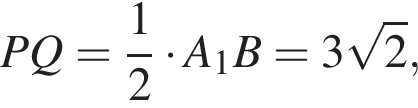



 значит, FD — диаметр, а
значит, FD — диаметр, а 
 тогда
тогда 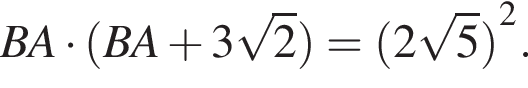 Значит,
Значит,  откуда
откуда  Таким образом,
Таким образом, 
 а тогда
а тогда 
 откуда
откуда 

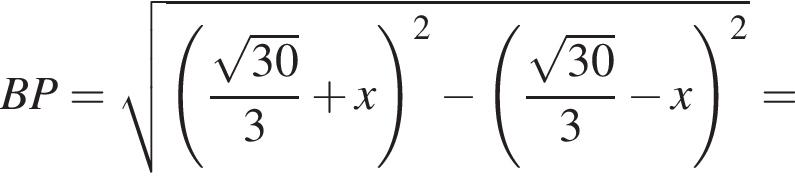


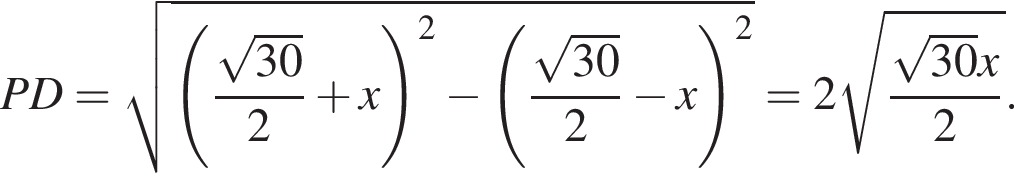





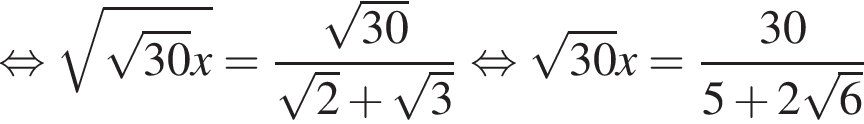

 б)
б) 


 а значит, и
а значит, и 
 Теперь найдем радиус окружности, описанной около треугольника ABD:
Теперь найдем радиус окружности, описанной около треугольника ABD:






 AE = 8.
AE = 8. 
 Следовательно, DE = 18.
Следовательно, DE = 18.


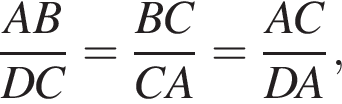



 Значит:
Значит: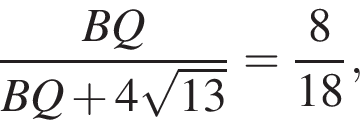




 отсюда следует
отсюда следует 

 то
то 


 откуда
откуда  Далее,
Далее,  откуда
откуда 

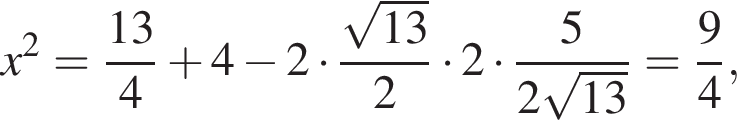
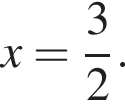
 как вписанные (опираются на дугу АС).
как вписанные (опираются на дугу АС). как вписанные (опираются на дугу AL). Тогда
как вписанные (опираются на дугу AL). Тогда  и треугольники PCL и BCL равны по стороне и двум прилежащим к ней углам. Следовательно,
и треугольники PCL и BCL равны по стороне и двум прилежащим к ней углам. Следовательно, 
 Треугольники ALK и CLB подобны по двум углам, тогда
Треугольники ALK и CLB подобны по двум углам, тогда  Кроме того, по свойству биссектрисы
Кроме того, по свойству биссектрисы 
 (1);
(1); 




 Обозначим угол
Обозначим угол  Тогда
Тогда 



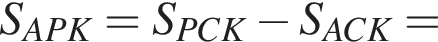




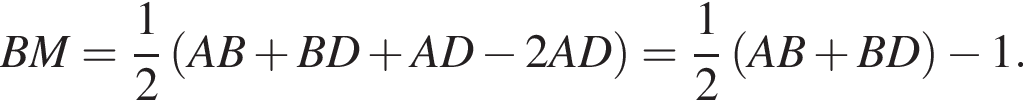






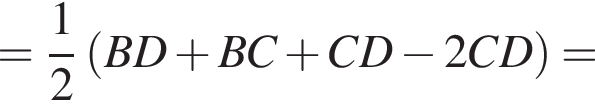





 Заметим, что площадь треугольника ABD равна двум площадям BDC. Получим:
Заметим, что площадь треугольника ABD равна двум площадям BDC. Получим:




 угол
угол  угол
угол 

 то есть
то есть  Тогда угол AEB равен 45°, откуда угол BAE равен 90°. Следовательно, BE — диаметр окружности.
Тогда угол AEB равен 45°, откуда угол BAE равен 90°. Следовательно, BE — диаметр окружности. Далее найдем:
Далее найдем:





 Площадь треугольника ABC можно вычислить, например, по формуле Герона, получится 48. Тогда радиус вписанной окружности равен
Площадь треугольника ABC можно вычислить, например, по формуле Герона, получится 48. Тогда радиус вписанной окружности равен 
 отсюда
отсюда  M2E = 4 и площадь треугольника BM2E равна 6. Обозначим вершину пятиугольника, лежащую на отрезке AC, буквой F. Заметим, что
M2E = 4 и площадь треугольника BM2E равна 6. Обозначим вершину пятиугольника, лежащую на отрезке AC, буквой F. Заметим, что 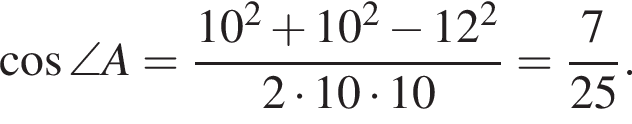

 и площадь треугольника AM1F равна
и площадь треугольника AM1F равна 

 и
и  Пусть точка E — середина FK, тогда
Пусть точка E — середина FK, тогда 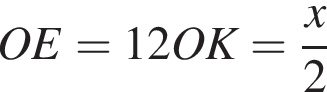 и
и  Значит,
Значит,  следовательно,
следовательно, 









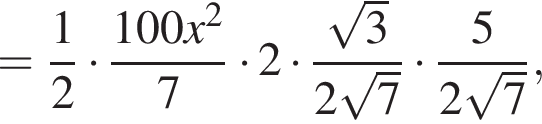

 то
то




 и что
и что 
 Найдите R.
Найдите R.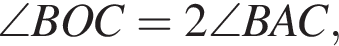 поэтому
поэтому  и, значит,
и, значит, 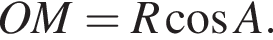 По неравенству треугольника
По неравенству треугольника 
 Что и требовалось доказать.
Что и требовалось доказать.  то центр описанной окружности лежит на медиане AM. Тогда треугольник ABC равнобедренный:
то центр описанной окружности лежит на медиане AM. Тогда треугольник ABC равнобедренный:  Углы CBH и CAM равны, поэтому равны углы MBH и MAB. Следовательно, треугольники MBH и MAB подобны. Получаем, что
Углы CBH и CAM равны, поэтому равны углы MBH и MAB. Следовательно, треугольники MBH и MAB подобны. Получаем, что 
 Пусть точка O — центр описанной около ABC окружности. Тогда по теореме Пифагора
Пусть точка O — центр описанной около ABC окружности. Тогда по теореме Пифагора  то есть
то есть  Решая это уравнение, получаем ответ: R = 7.
Решая это уравнение, получаем ответ: R = 7. 
 откуда
откуда 
 а
а  Следовательно, точка O действительно ближе к точке M, чем точка H.
Следовательно, точка O действительно ближе к точке M, чем точка H. высота
высота  и биссектриса
и биссектриса 
 Тогда из равнобедренного треугольника BOC
Тогда из равнобедренного треугольника BOC  и
и  Углы BAC и BOC опираются на одну дугу, поэтому
Углы BAC и BOC опираются на одну дугу, поэтому 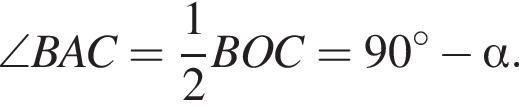 В прямоугольном треугольнике ABH:
В прямоугольном треугольнике ABH:



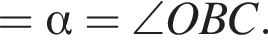











 Пусть
Пусть  По свойству биссектрисы в треугольнике HBO получаем:
По свойству биссектрисы в треугольнике HBO получаем: