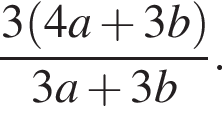В трапеции ABCD с боковыми сторонами AB = 8 и CD = 5 биссектриса угла B пересекает биссектрисы углов A и C в точках M и N соответственно, а биссектриса угла D пересекает те же две биссектрисы в точках L и K, причем точка L лежит на основании BC.
а) Докажите, что прямая MK проходит через середину стороны AB.
б) Найти отношение KL : MN, если LM : KN = 4 : 7.
Решение.
а) Обозначим буквой E точку пересечения отрезков MK и AB. Углы ∠ALB и ∠LAD равны, как накрест лежащие углы; аналогично ∠CLD = ∠ADL, как накрест лежащие. Отсюда получаем, что ∠BAL = ∠BLA, ∠CDL = ∠CLD, то есть треугольники ABL и CLD равнобедренные (AB = BL, CL = CD). Тогда биссектрисы этих треугольников BM и CK являются также высотами и медианами. Значит, точки M и K являются серединами сторон AL и DL соответственно. Отсюда следует, что отрезок MK является средней линией треугольника ALD. Значит, MK || AD.
Теперь если рассмотреть треугольник ABL, получаем, что отрезок EM параллелен стороне BL и исходит из середины стороны AL. Отсюда следует, что EM является средней линией этого треугольника, а значит точка E — середина стороны AB. Что и требовалось доказать.
б) Рассмотрим 4-угольник MLKN. Из предыдущего пункта получили, что ∠M = 90°, ∠K = 90°, откуда следует, что

То есть у данного 4-угольника суммы противоположных углов дают ![]() откуда следует, что вокруг него можно описать окружность. Соединим точки N и L (пересечение с MK в точке F) — получим 2 прямоугольных треугольника NML и NKL. Тогда центр описанной окружности лежит на середине общей гипотенузы NL.
откуда следует, что вокруг него можно описать окружность. Соединим точки N и L (пересечение с MK в точке F) — получим 2 прямоугольных треугольника NML и NKL. Тогда центр описанной окружности лежит на середине общей гипотенузы NL.
Теперь заметим, что треугольники MFL и NFK подобны по 2 углам (∠MFL = ∠NFK, как вертикальные; ∠MLF = ∠NKF, как вписанные углы, опирающиеся на одну и ту же дугу MN). Тогда 
Аналогично треугольники NMF и KFL подобны по 2 углам (∠NFM = ∠KFL, как вертикальные; ∠MNF = ∠FKL, как вписанные углы, опирающиеся на одну и ту же дугу ML). Тогда 
Поделим соотношения друг на друга:

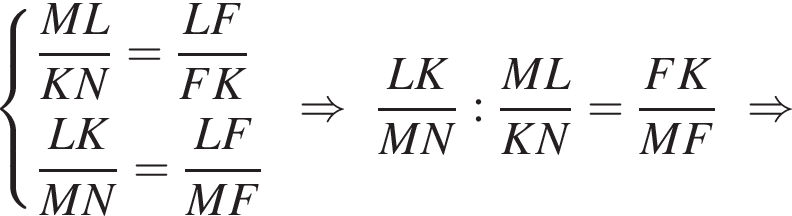




Из подобия треугольников NLC и NFK (по 3-м углам) получим, что  Аналогично из подобия треугольников NLB и NFM получим, что
Аналогично из подобия треугольников NLB и NFM получим, что  откуда следует:
откуда следует:
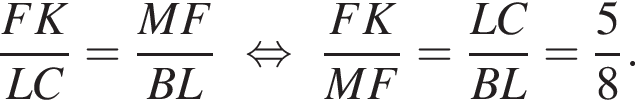
Окончательно получаем, что

Ответ: 5 : 14.
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б. | 3 |
| Получен обоснованный ответ в пункте б. ИЛИ Имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. | 2 |
| Имеется верное доказательство утверждения пункта а. ИЛИ При обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. ИЛИ Обоснованно получен верный ответ в пункте б и использованием утверждения пункта а, при этом пункт а не выполнен. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 3 |
 По теореме Фалеса получаем
По теореме Фалеса получаем  откуда
откуда

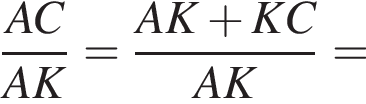


 откуда MK = NL. Что и требовалось доказать.
откуда MK = NL. Что и требовалось доказать.

 и выпишем полученную систему двух уравнений:
и выпишем полученную систему двух уравнений:
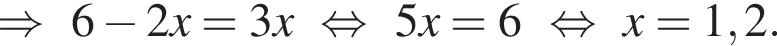

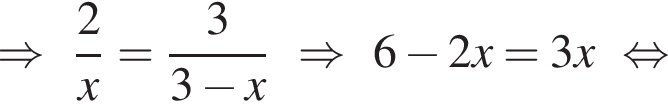





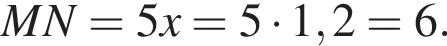
 из треугольника KON
из треугольника KON  Далее получим, что
Далее получим, что 
 откуда
откуда  Что и требовалось доказать.
Что и требовалось доказать. Теперь если рассмотреть треугольник KMN, то в нем CD является средней линией. Тогда
Теперь если рассмотреть треугольник KMN, то в нем CD является средней линией. Тогда  Отсюда получаем, что
Отсюда получаем, что  Аналогично доказывается, что
Аналогично доказывается, что 
 Аналогично доказывается из площадей треугольников MBO и NDO, что
Аналогично доказывается из площадей треугольников MBO и NDO, что 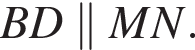 Значит,
Значит,  и KLMN — трапеция.
и KLMN — трапеция.
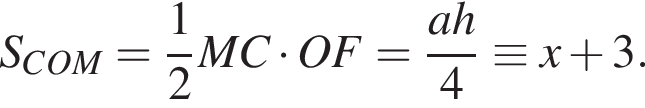




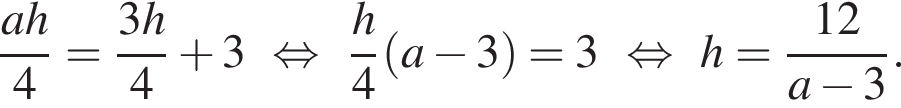


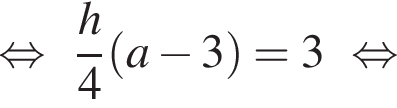


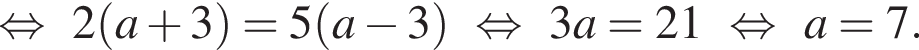





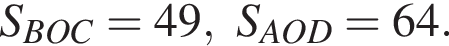

 имеем
имеем






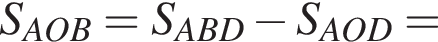











 тогда
тогда 

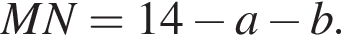 Отметим на MN точку T такую, что
Отметим на MN точку T такую, что 
 На продолжении CB а точку B отметим точку K так, чтобы
На продолжении CB а точку B отметим точку K так, чтобы 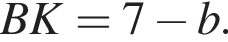 Тогда
Тогда 

 поэтому A лежит на биссектрисе угла KMN.
поэтому A лежит на биссектрисе угла KMN.
 поэтому B и D — точки касания.
поэтому B и D — точки касания.
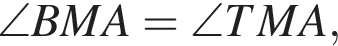 AM — общая). Значит,
AM — общая). Значит,  Кроме того,
Кроме того,  Тогда треугольники TNA и DNA равны по катету и гипотенузе, поэтому
Тогда треугольники TNA и DNA равны по катету и гипотенузе, поэтому 





 четырехугольник AODE — вписанный. Значит,
четырехугольник AODE — вписанный. Значит,  (как хорды, стягивающие равные дуги в его описанной окружности. Равенство дуг следует из равенства углов AOE и DOE).
(как хорды, стягивающие равные дуги в его описанной окружности. Равенство дуг следует из равенства углов AOE и DOE). Тогда
Тогда 





 тогда треугольники
тогда треугольники 





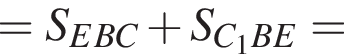
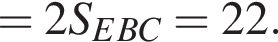

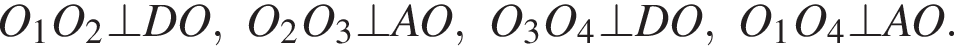
 — параллелограмм,
— параллелограмм,  Ясно, что также
Ясно, что также 
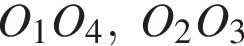 — серединные перпендикуляры к отрезкам АО и СО, то
— серединные перпендикуляры к отрезкам АО и СО, то 
 Значит,
Значит,  т. е
т. е 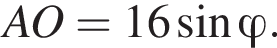
 где
где  ВО = 6.
ВО = 6. т. е.
т. е. 
 Разделим обе части равенства на
Разделим обе части равенства на  Получим:
Получим:

















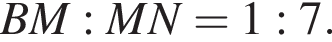 Найдите BC, если AB = 12.
Найдите BC, если AB = 12. выполняться не будет.
выполняться не будет. (по условию),
(по условию),  как внутренние накрест лежащие при параллельных ВС и AD, секущей АМ. Значит,
как внутренние накрест лежащие при параллельных ВС и AD, секущей АМ. Значит,  по свойству транзитивности равенства. Отсюда BM = AB = 12.
по свойству транзитивности равенства. Отсюда BM = AB = 12.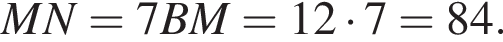 Тогда
Тогда 

 тогда
тогда 

 откуда
откуда  Следовательно, BM = 12, и
Следовательно, BM = 12, и 
 Найдите диагональ LN.
Найдите диагональ LN. значит,
значит,  — тупой,
— тупой,  — острый,
— острый, 










 — тупой,
— тупой, 











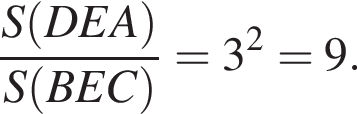 Значит,
Значит, 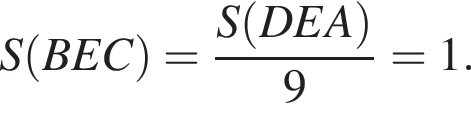
 Треугольники АСD и АВD также равновелики как имеющие одно и тоже основание АD и равные высоты, проведенные к этой стороне.
Треугольники АСD и АВD также равновелики как имеющие одно и тоже основание АD и равные высоты, проведенные к этой стороне. 



 Значит,
Значит, 



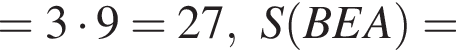









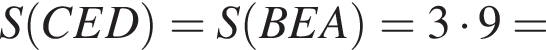


 ) проведена высота BH. Обозначим
) проведена высота BH. Обозначим 
 Тогда
Тогда 

 Кроме того,
Кроме того,  Тогда
Тогда 
 и по теореме, обратной к теореме Виета, получаем
и по теореме, обратной к теореме Виета, получаем  или
или 
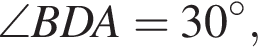 то
то  и
и  В этом случае AD — большее основание.
В этом случае AD — большее основание.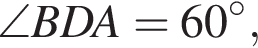 то
то  и
и  В этом случае AD — меньшее основание, а острый угол трапеции равен
В этом случае AD — меньшее основание, а острый угол трапеции равен 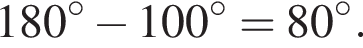


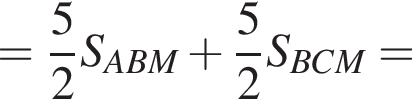


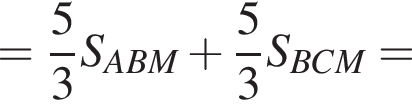

 E — точка касания на стороне CD, CE = 8, ED = 18. Пусть также O — центр вписанной окружности. Тогда треугольник COD прямоугольный (так как CO и DO — биссектрисы односторонних углов трапеции). OE — его высота, опущенная на гипотенузу, поэтому
E — точка касания на стороне CD, CE = 8, ED = 18. Пусть также O — центр вписанной окружности. Тогда треугольник COD прямоугольный (так как CO и DO — биссектрисы односторонних углов трапеции). OE — его высота, опущенная на гипотенузу, поэтому Итак, радиус окружности равен 12. Поэтому высота трапеции равна 24.
Итак, радиус окружности равен 12. Поэтому высота трапеции равна 24. откуда AB = 30.
откуда AB = 30. из треугольника CDH получим
из треугольника CDH получим 














 Проведем через C прямую, параллельную BD. Она пересечет продолжение AD в точке
Проведем через C прямую, параллельную BD. Она пересечет продолжение AD в точке  — параллелограмм, и площадь равна
— параллелограмм, и площадь равна 



 Опустим его высоту
Опустим его высоту  Тогда
Тогда 
 откуда
откуда  и
и 



 и
и 



 и
и 


 как вертикальные,
как вертикальные,  как внутренние накрест лежащие углы при параллельных ВС, DF и секущей CD.
как внутренние накрест лежащие углы при параллельных ВС, DF и секущей CD. Значит, параллелограмм ABEF — ромб (по признаку ромба). Отсюда следует, что ВР — биссектриса угла АВС.
Значит, параллелограмм ABEF — ромб (по признаку ромба). Отсюда следует, что ВР — биссектриса угла АВС. 


 Коли это так, то S(PBC) = S(FPD).
Коли это так, то S(PBC) = S(FPD).



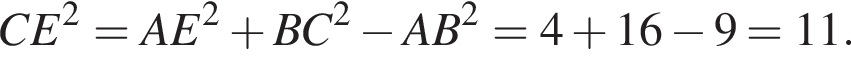

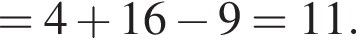


 Следовательно,
Следовательно, 



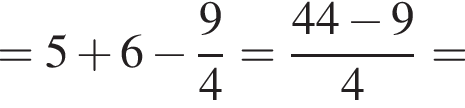

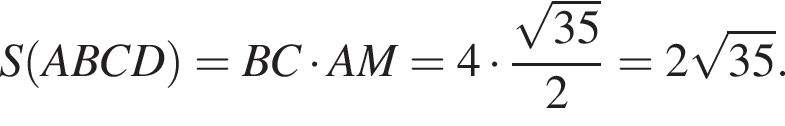
 получаем
получаем  поэтому в четырехугольник ABCD можно вписать окружность.
поэтому в четырехугольник ABCD можно вписать окружность. (*). Пусть p — полупериметр каждого из данных треугольников, тогда из (*) получаем:
(*). Пусть p — полупериметр каждого из данных треугольников, тогда из (*) получаем:  откуда находим искомый радиус:
откуда находим искомый радиус:  (Известное свойство (*) нетрудно доказать, пользуясь тем, что площадь каждого из треугольников равна половине произведения сторон на синус заключенного между ними угла.)
(Известное свойство (*) нетрудно доказать, пользуясь тем, что площадь каждого из треугольников равна половине произведения сторон на синус заключенного между ними угла.) 




 а площадь вписанного круга равна
а площадь вписанного круга равна 
 Так как около окружности можно описать четырехугольник в том и только в том случае, если суммы противолежащих его сторон равны, то сумма оснований трапеции будет равна сумме ее боковых сторон, т. е. AD + BC = a + b.
Так как около окружности можно описать четырехугольник в том и только в том случае, если суммы противолежащих его сторон равны, то сумма оснований трапеции будет равна сумме ее боковых сторон, т. е. AD + BC = a + b.









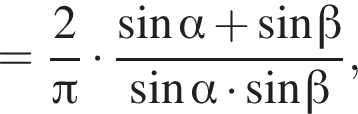

 значит,
значит, 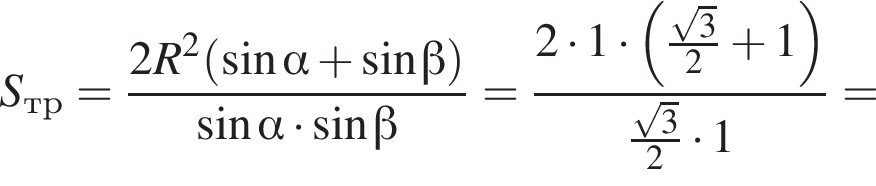






 Так как BK || AC, то
Так как BK || AC, то  т. е.
т. е.  Следовательно, около
Следовательно, около 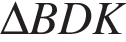 можно описать окружность с центром в точке Н и радиусом R = BH = KH = DH. Итак,
можно описать окружность с центром в точке Н и радиусом R = BH = KH = DH. Итак, 
 т. е.
т. е. 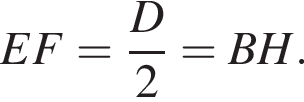 Отсюда вывод: в равнобочной трапеции, у которого диагонали взаимно перпендикулярны, высота равна средней линии этой же трапеции.
Отсюда вывод: в равнобочной трапеции, у которого диагонали взаимно перпендикулярны, высота равна средней линии этой же трапеции.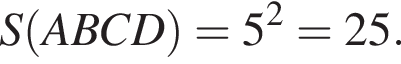
 Значит,
Значит, 
 как внутренние накрест лежащие при параллельных ВА, СD и секущей ВD. Следовательно,
как внутренние накрест лежащие при параллельных ВА, СD и секущей ВD. Следовательно,  В таком случае в
В таком случае в  где
где 
 — равнобедренный, т. е. BH = DH, что и требовалось доказать.
— равнобедренный, т. е. BH = DH, что и требовалось доказать. откуда
откуда
 Отсюда
Отсюда 


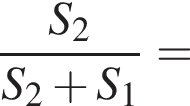



 откуда
откуда


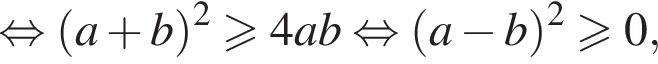





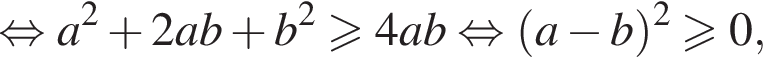







 — середина отрезка
— середина отрезка 

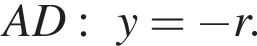






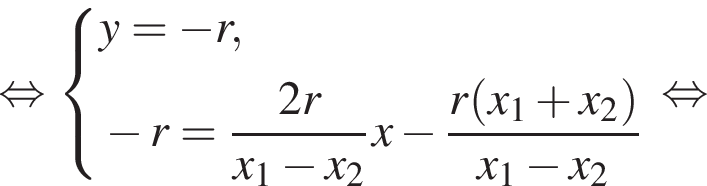











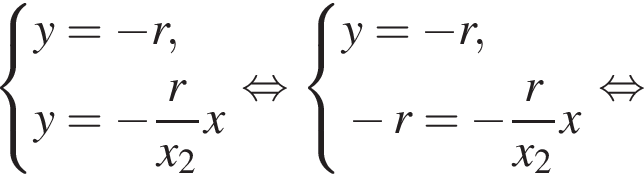


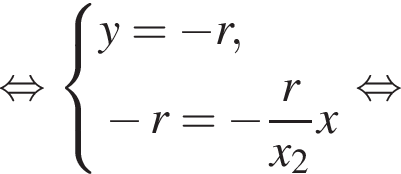

 По признаку окружности , вписанной в четырехугольник:
По признаку окружности , вписанной в четырехугольник: 

 Значит,
Значит, 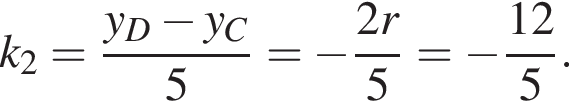

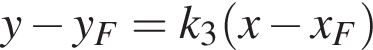 или
или 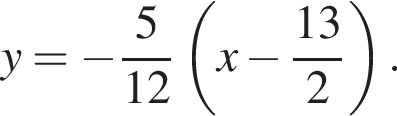











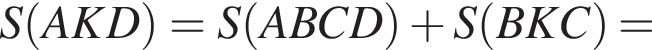




 (ABCD — параллелограмм по признаку параллелограмма), что и требовалось доказать.
(ABCD — параллелограмм по признаку параллелограмма), что и требовалось доказать.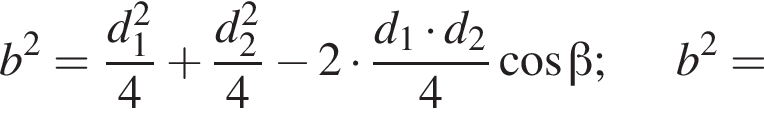

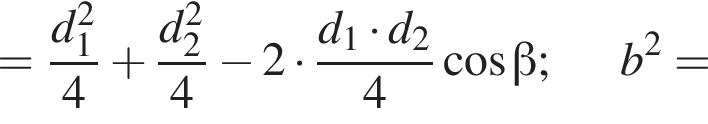



 откуда
откуда 
















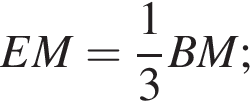






 Следовательно,
Следовательно, 



 Тогда:
Тогда: 
 Но равновеликие
Но равновеликие  что в свою очередь свидетельствует о том, что точки A и D одинаково удалены от прямой
что в свою очередь свидетельствует о том, что точки A и D одинаково удалены от прямой 
 и
и 

 Очевидно, что
Очевидно, что 
 Пусть
Пусть 
 Тогда:
Тогда: 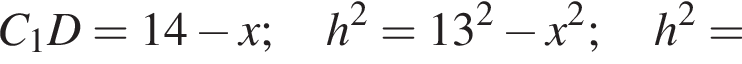




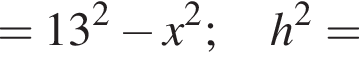



 как накрест лежащие, образованные при пересечении двух параллельных прямых третьей-секущей;
как накрест лежащие, образованные при пересечении двух параллельных прямых третьей-секущей;  как вертикальные, откуда:
как вертикальные, откуда: 





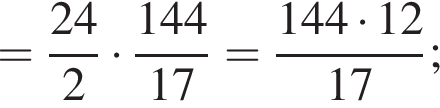


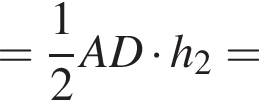

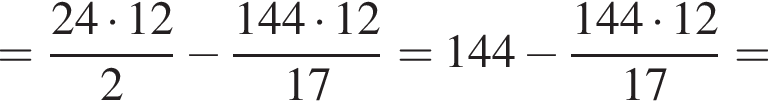








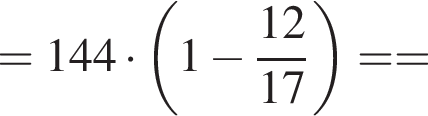

 если
если 
 из равенства треугольников ABK и CBK по первому признаку. Обозначим за E середину
из равенства треугольников ABK и CBK по первому признаку. Обозначим за E середину 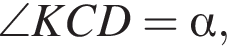 тогда
тогда  (из параллельности стороны и серединного перпендикуляра к другой стороне).
(из параллельности стороны и серединного перпендикуляра к другой стороне). 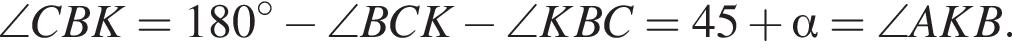
 то
то  тогда
тогда  откуда треугольник CBM — равнобедренный. Значит,
откуда треугольник CBM — равнобедренный. Значит,  то есть
то есть  и
и 


 Найдем координаты пересечения этой прямой с осью x:
Найдем координаты пересечения этой прямой с осью x:  Итак,
Итак, 
 и уравнение прямой AO:
и уравнение прямой AO:  Пусть B — точка их пересечения. Подставляя, имеем:
Пусть B — точка их пересечения. Подставляя, имеем: 
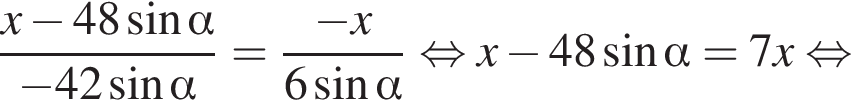

 и
и 







 и уравнение прямой AO:
и уравнение прямой AO: 


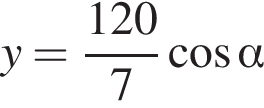 и
и 




 откуда
откуда  и
и 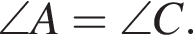

 Так как PM и QN делят треугольник ABC на три равновеликие части, что
Так как PM и QN делят треугольник ABC на три равновеликие части, что  Если сложить треугольники APM и QNC по большему катету, то получится треугольник подобный ABC, с коэффициентом подобия равным
Если сложить треугольники APM и QNC по большему катету, то получится треугольник подобный ABC, с коэффициентом подобия равным  Имеем:
Имеем:

 или
или 


 и
и  Тогда
Тогда  откуда
откуда  и
и  откуда
откуда  Следовательно, треугольники ADE и BGF равны, и
Следовательно, треугольники ADE и BGF равны, и 
 тогда из подобия треугольников AGL и ADE следует, что
тогда из подобия треугольников AGL и ADE следует, что  то есть
то есть  Тогда
Тогда 









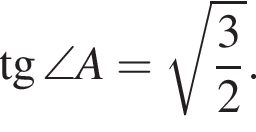








 или
или  или
или 


 и по теореме косинусов для треугольника MCK имеем
и по теореме косинусов для треугольника MCK имеем
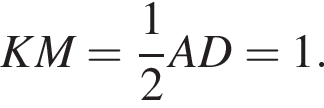

 откуда
откуда  поэтому M — середина AD.
поэтому M — середина AD.
 откуда
откуда 
 поэтому
поэтому 
 откуда
откуда  Тогда
Тогда 
 Аналогично
Аналогично  поэтому треугольники AKE и MCP имеют суммарную площадь
поэтому треугольники AKE и MCP имеют суммарную площадь 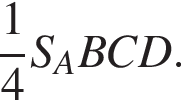 Аналогично и треугольники BKM и EPD. Значит, на долю KMPE приходится
Аналогично и треугольники BKM и EPD. Значит, на долю KMPE приходится  что и требовалось.
что и требовалось. и
и  поэтому KMPE — параллелограмм. Причем
поэтому KMPE — параллелограмм. Причем 




 откуда углы параллелограмма — 60° и 120°. В таком случае его большая диагональ равна по теореме косинусов
откуда углы параллелограмма — 60° и 120°. В таком случае его большая диагональ равна по теореме косинусов 
 поэтому
поэтому 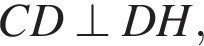 следовательно, CD — касательная.
следовательно, CD — касательная.
 поэтому
поэтому 
 по теореме косинусов находим
по теореме косинусов находим 

 Это и есть ответ.
Это и есть ответ. Длина общей хорды в два раза больше высоты треугольника со сторонами
Длина общей хорды в два раза больше высоты треугольника со сторонами  проведенной к большей стороне. Значит,
проведенной к большей стороне. Значит, 



 то условие задачи выполняется. Очевидно при увеличении CN будет уменьшаться AM и наоборот, поэтому ситуация равных отношений возможна лишь один раз.
то условие задачи выполняется. Очевидно при увеличении CN будет уменьшаться AM и наоборот, поэтому ситуация равных отношений возможна лишь один раз.  тогда
тогда 
 Значит,
Значит,  тогда по теореме синусов
тогда по теореме синусов  откуда
откуда  и Значит,
и Значит, 


 ? следоваельно в треугольнике ABP медиана PQ равна половине стороны AB, поэтому
? следоваельно в треугольнике ABP медиана PQ равна половине стороны AB, поэтому 

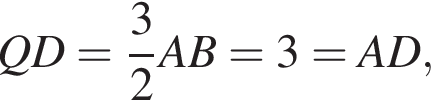 треугольник равнобедренный), окончательный ответ
треугольник равнобедренный), окончательный ответ 
 и
и  — прямоугольные с общим острым углом
— прямоугольные с общим острым углом 
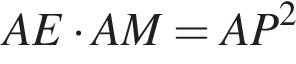 и
и  откуда
откуда 
 а тогда
а тогда  наконец, углы MEF и MKC равны как вписанные, опирающиеся на дугу MF. Тогда
наконец, углы MEF и MKC равны как вписанные, опирающиеся на дугу MF. Тогда  а это соответственные углы при прямых EF и AB, которые пересекает секущая AC. Тем самым, данные прямые параллельны, и
а это соответственные углы при прямых EF и AB, которые пересекает секущая AC. Тем самым, данные прямые параллельны, и  Подставляя полученное соотношение в равенство (1), находим:
Подставляя полученное соотношение в равенство (1), находим: 
 и
и  — прямоугольные,
— прямоугольные,  Полагая PN = x, получаем:
Полагая PN = x, получаем: 
 и
и  также прямоугольные,
также прямоугольные,  Отсюда находим, что
Отсюда находим, что 
 Подставляя (2), получим уравнение
Подставляя (2), получим уравнение  Его единственным решением является
Его единственным решением является 
 Значит,
Значит, 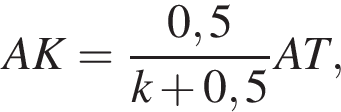 Значит,
Значит, 
 поэтому
поэтому  Следовательно, OE - средняя линия CKD и
Следовательно, OE - средняя линия CKD и 

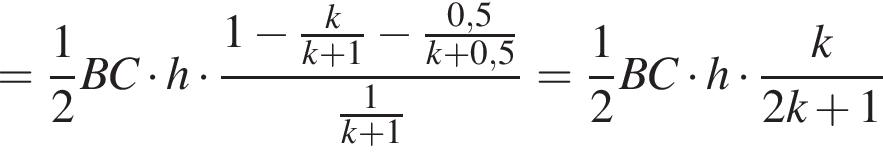

 откуда
откуда 


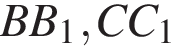 — высоты. Тогда
— высоты. Тогда  и поэтому
и поэтому  то есть
то есть  что и требовалось.
что и требовалось.
 поэтому
поэтому 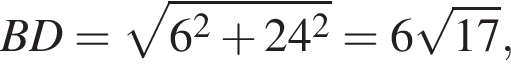 откуда
откуда 
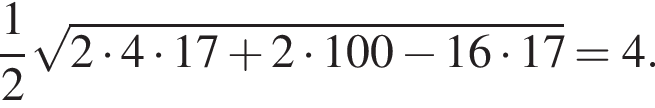
 из которых
из которых  приходятся на углы, прилегающие к пятиугольнику (два набора его внешних углов). Поэтому сумма углов при вершинах равна
приходятся на углы, прилегающие к пятиугольнику (два набора его внешних углов). Поэтому сумма углов при вершинах равна 













 Применяя формулу для медианы, преобразуем условие в двойное неравенство.
Применяя формулу для медианы, преобразуем условие в двойное неравенство.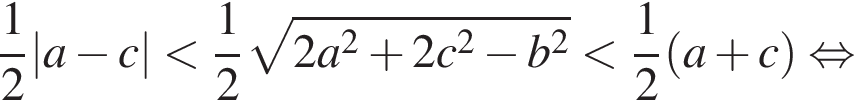

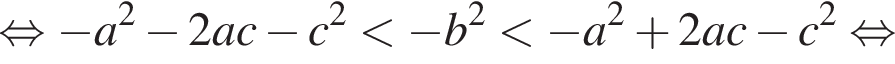



 откуда
откуда 




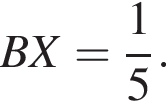
 Прямая, перпендикулярная
Прямая, перпендикулярная  откуда и следует подобие треугольников ABN и DCM по двум углам.
откуда и следует подобие треугольников ABN и DCM по двум углам. где k — коэффициент подобия треугольников из п. а). Значит,
где k — коэффициент подобия треугольников из п. а). Значит, 
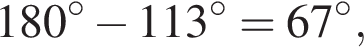 поэтому ударится о другой борт под углом
поэтому ударится о другой борт под углом  Аналогично в следующий раз угол станет
Аналогично в следующий раз угол станет 

 откуда
откуда 
 Поскольку
Поскольку 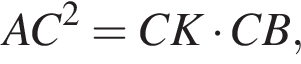 прямая AC является касательной к окружности.
прямая AC является касательной к окружности.


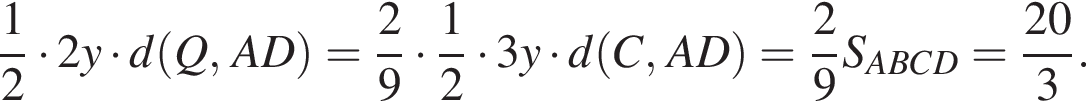


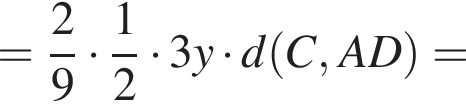







 опирается на диаметр MA, он прямой. Тогда треугольник AFK тоже прямоугольный и середина AK — его центр описанной окружности. Поскольку треугольники ABD и BMC равны по двум катетам, а треугольники MBC и CDK равны по катету и острому углу, то
опирается на диаметр MA, он прямой. Тогда треугольник AFK тоже прямоугольный и середина AK — его центр описанной окружности. Поскольку треугольники ABD и BMC равны по двум катетам, а треугольники MBC и CDK равны по катету и острому углу, то  так что центро окружности является точка D и
так что центро окружности является точка D и 

 откуда, учитывая
откуда, учитывая  и
и  находим
находим 


 по теореме косинусов получаем
по теореме косинусов получаем 

 Поскольку
Поскольку  следует взять
следует взять  то есть
то есть  и
и 
 откуда
откуда 





 и
и 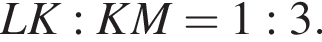
 и
и  Тогда
Тогда  и
и  — параллелограммы (их диагонали делятся точками пересечения пополам). Тогда
— параллелограммы (их диагонали делятся точками пересечения пополам). Тогда  и
и  как соответственные. Значит, треугольники
как соответственные. Значит, треугольники  Тогда и
Тогда и  откуда следует подобие треугольников BKC и DKA по углу и двум парам пропорциональных сторон. Значит,
откуда следует подобие треугольников BKC и DKA по углу и двум парам пропорциональных сторон. Значит,  то есть прямая BC параллельна прямой AD, что и требовалось доказать.
то есть прямая BC параллельна прямой AD, что и требовалось доказать.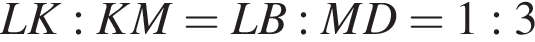 из подобия треугольников BLK и KMD по двум углам. Пусть
из подобия треугольников BLK и KMD по двум углам. Пусть 
 Из условия описанности
Из условия описанности 
 и напишем теорему косинусов для треугольников BCA и CAD:
и напишем теорему косинусов для треугольников BCA и CAD:







 Поскольку
Поскольку 
 поэтому AB — высота трапеции. Радиус окружности, очевидно, равен половине этой высоты.
поэтому AB — высота трапеции. Радиус окружности, очевидно, равен половине этой высоты.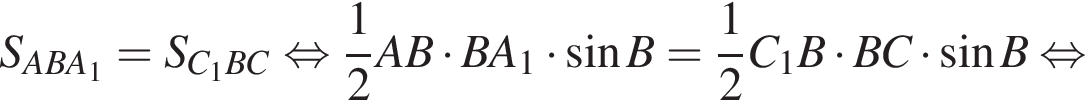















 Тогда:
Тогда:



 Кроме того,
Кроме того, 
 Далее,
Далее,  следовательно, прямая
следовательно, прямая 

 Следовательно,
Следовательно,  — равнобедренная трапеция, а углы BAD, ADC и BCD равны. Значит, в ABCD три равных угла: 108°, 108°, 108° и 36° или 108°, 84°, 84° или 84°.
— равнобедренная трапеция, а углы BAD, ADC и BCD равны. Значит, в ABCD три равных угла: 108°, 108°, 108° и 36° или 108°, 84°, 84° или 84°. Длины оснований BC и AD относятся как
Длины оснований BC и AD относятся как 
 поэтому
поэтому 
 По теореме Менелая для треугольника CAB и прямой NMT имеем:
По теореме Менелая для треугольника CAB и прямой NMT имеем:  откуда
откуда 
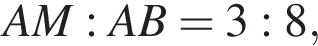 поэтому:
поэтому:
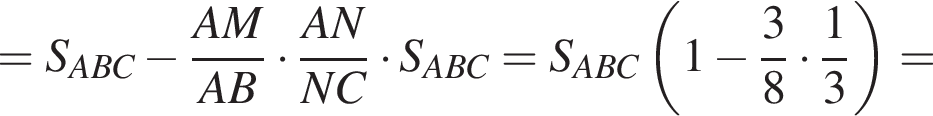


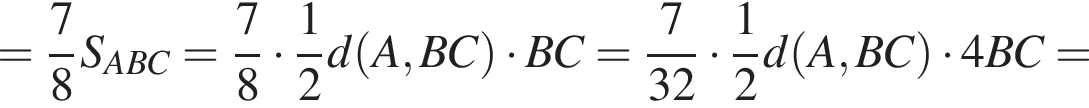







 Значит, треугольники DNH и DMS подобны с коэффициентом
Значит, треугольники DNH и DMS подобны с коэффициентом  Тогда
Тогда  и
и 
 Окружность ω с центром в точке M касается прямой AC и пересекает прямую KL в точках P и Q,
Окружность ω с центром в точке M касается прямой AC и пересекает прямую KL в точках P и Q, 



 тогда
тогда 



 Значит,
Значит,  Тогда
Тогда  и радиус окружности равен
и радиус окружности равен 


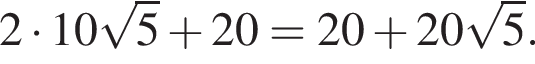




 Пусть
Пусть  тогда KN — высота равностороннего треугольника со стороной
тогда KN — высота равностороннего треугольника со стороной 







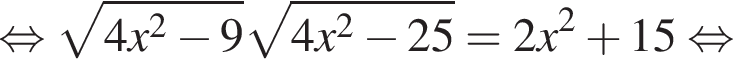



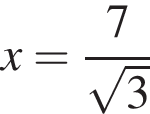 и
и  Тогда
Тогда 



 получаем
получаем  Далее:
Далее:








 и
и 


 а
а 








 Поскольку C, T, A лежат на одной прямой, отсюда следует, что O, T, Q лежат на одной прямой, что и требовалось доказать.
Поскольку C, T, A лежат на одной прямой, отсюда следует, что O, T, Q лежат на одной прямой, что и требовалось доказать. поскольку
поскольку 
 ). Поэтому точки R, T, N лежат на одной прямой. Коэффициент подобия треугольников равен
). Поэтому точки R, T, N лежат на одной прямой. Коэффициент подобия треугольников равен 


 потому что это радиусы вписанной окружности треугольника ABC. Тогда
потому что это радиусы вписанной окружности треугольника ABC. Тогда 
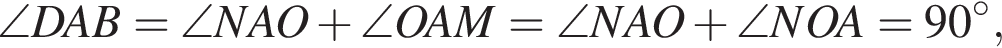


 Пусть
Пусть  тогда
тогда  (здесь за x обозначена длина отрезка от вершины C до точек касания со сторонами CB и CA). По теореме Пифагора имеем
(здесь за x обозначена длина отрезка от вершины C до точек касания со сторонами CB и CA). По теореме Пифагора имеем 



 и
и 

 сторона
сторона  Продолжения боковых сторон пересекаются в точке K, образуя прямой угол AKD. Окружность ω проходит через точки А и В и касается стороны CD в точке P.
Продолжения боковых сторон пересекаются в точке K, образуя прямой угол AKD. Окружность ω проходит через точки А и В и касается стороны CD в точке P. поэтому
поэтому  Значит,
Значит,  откуда
откуда  и
и  По теореме Пифагора для треугольника BKC находим
По теореме Пифагора для треугольника BKC находим 





 и T — середина AB, то прямая OT перпендикулярна прямой AK. Значит, TKPO — прямоугольник (его углы T, K и P — прямые). Значит,
и T — середина AB, то прямая OT перпендикулярна прямой AK. Значит, TKPO — прямоугольник (его углы T, K и P — прямые). Значит, 
 б) 10.
б) 10. следовательно,
следовательно, 
 Следовательно,
Следовательно,  и
и  Отсюда AMOH — параллелограмм с прямым углом, следовательно, AMOH — прямоугольник. Значит,
Отсюда AMOH — параллелограмм с прямым углом, следовательно, AMOH — прямоугольник. Значит, 
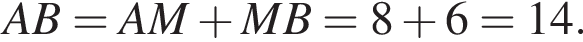
 тогда
тогда







 значит, прямая A1A2 параллельна прямой A5A3.
значит, прямая A1A2 параллельна прямой A5A3. Пусть
Пусть  Тогда
Тогда 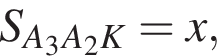



 Тогда для треугольника A1A2A3 получаем:
Тогда для треугольника A1A2A3 получаем:
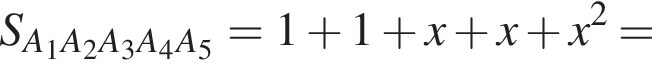




 Таким образом,
Таким образом, 

 таким образом, треугольники MHN и NLR подобны. Тогда
таким образом, треугольники MHN и NLR подобны. Тогда 

 Тогда
Тогда  откуда
откуда 
 значит,
значит,  Пусть
Пусть  сумма углов треугольника ACD равна
сумма углов треугольника ACD равна  Отсюда
Отсюда  что и требовалось доказать.
что и требовалось доказать. Тогда большее основание AD равно
Тогда большее основание AD равно  Высота трапеции равна
Высота трапеции равна  Следовательно, для площади трапеции получаем:
Следовательно, для площади трапеции получаем: 


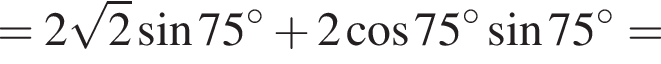




 Тогда высоты трапеций FLMP и KFPN равны, поэтому их площади относятся как
Тогда высоты трапеций FLMP и KFPN равны, поэтому их площади относятся как 
 Поэтому площадь треугольника FEP составляет
Поэтому площадь треугольника FEP составляет 
 то есть
то есть  Теперь заметим, что треугольники LME и FPN подобны по двум пропорциональным сторонам и углу между ними. Отсюда углы MEL и PNF равны, поэтому прямые LE и FN параллельны. Что и требовалось доказать.
Теперь заметим, что треугольники LME и FPN подобны по двум пропорциональным сторонам и углу между ними. Отсюда углы MEL и PNF равны, поэтому прямые LE и FN параллельны. Что и требовалось доказать.
 Заметим, что
Заметим, что 

 Затем, треугольник LEK равнобедренный (высота в нем совпадает с медианой). Поэтому
Затем, треугольник LEK равнобедренный (высота в нем совпадает с медианой). Поэтому 
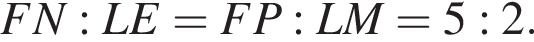

 и
и  Через середину отрезка CD проведена прямая, пересекающая стороны АС и ВС в точках M и N соответственно. Известно, что
Через середину отрезка CD проведена прямая, пересекающая стороны АС и ВС в точках M и N соответственно. Известно, что  площадь треугольника MCN равна
площадь треугольника MCN равна  откуда
откуда 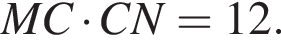 Положим
Положим  По условию,
По условию,  то есть
то есть 
 то есть
то есть  Следовательно,
Следовательно, 




 Решая систему на CM и CN получаем, что CM = 3, CN = 4. Запишем теорему косинусов для треугольников CNE и CME, получим, что
Решая систему на CM и CN получаем, что CM = 3, CN = 4. Запишем теорему косинусов для треугольников CNE и CME, получим, что 



 Тогда диагонали четырехугольника DNCM точкой пересечения делятся пополам, значит, он является параллелограммом. Что и требовалось доказать.
Тогда диагонали четырехугольника DNCM точкой пересечения делятся пополам, значит, он является параллелограммом. Что и требовалось доказать.  В итоге, BC = 6, AC = 9, и площадь треугольника ABC равна
В итоге, BC = 6, AC = 9, и площадь треугольника ABC равна 




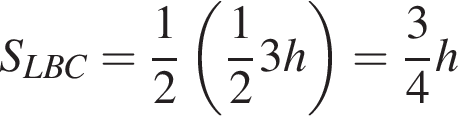

 Треугольники BCK и LMD подобны по двум пропорциональным сторонам и углу между ними, значит, равны углы BKC и MDL. Отсюда следует параллельность прямых BK и DL. Что и требовалось доказать.
Треугольники BCK и LMD подобны по двум пропорциональным сторонам и углу между ними, значит, равны углы BKC и MDL. Отсюда следует параллельность прямых BK и DL. Что и требовалось доказать.
 Значит, треугольники ECL и EAK подобны с коэффициентом 2 : 3, откуда AK = 6. KL — серединный перпендикуляр к AB, поэтому
Значит, треугольники ECL и EAK подобны с коэффициентом 2 : 3, откуда AK = 6. KL — серединный перпендикуляр к AB, поэтому  Наконец, треугольники BCK и LMD подобны с коэффициентом 1 : 2, поэтому
Наконец, треугольники BCK и LMD подобны с коэффициентом 1 : 2, поэтому 

 и
и 



 следовательно,
следовательно,  По теореме косинусов получаем, что
По теореме косинусов получаем, что


 тогда
тогда  а значит,
а значит, 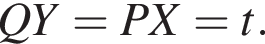 Находим:
Находим: 




 значит,
значит,