В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину В перпендикулярно АМ, пересекает сторону АС в точке N. АВ = 6; ВС = 5; АС = 9.
а) Докажите, что биссектриса угла С делит отрезок МN пополам.
б) Пусть Р — точка пересечения биссектрис треугольника АВС. Найдите отношение АР : РN.
Решение. а) Обозначим K точку пересечения отрезков AM и BN. Треугольник ABN равнобедренный, поскольку в нем AK является биссектрисой и высотой. Следовательно, AK является и медианой, то есть K — середина BN. Получаем, что AN = AB = 6, откуда NC = AC − AN = 3.
Рассмотрим треугольник ABC, биссектриса делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам: BM : MC = AB : AC, учитывая, что длина BC равна 5, получаем: BM = 2; MC = 3.
В треугольнике MNC стороны NC и MC равны, следовательно, треугольник MNC — равнобедренный, с основанием MN. Значит, биссектриса угла C также является медианой и высотой. Таким образом, получаем, что биссектриса угла С делит отрезок MN пополам.
б) Рассмотрим треугольник PMN: отрезок PO перпендикулярен прямой MN и делит её пополам, следовательно, треугольник PMN — равнобедренный с основанием MN. Значит, PM = PN и отношение AP : PN = AP : PM.
В треугольнике AMC отрезок CP — биссектриса, поэтому AP : PM = AC : MC = 3 : 1.
Ответ: 3 : 1.
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) ИЛИ имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) ИЛИ при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | 1 |
| Решение не соответствует ни одному из критериев, приведённых выше | 0 |
| Максимальный балл | 3 |

 AL = BC = KC . AC = CD.
AL = BC = KC . AC = CD.  что и требовалось доказать.
что и требовалось доказать. 





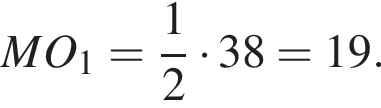
 а
а 




 откуда
откуда 








 Заметим, что
Заметим, что  как вписанные, опирающиеся на одну дугу. Значит,
как вписанные, опирающиеся на одну дугу. Значит, 




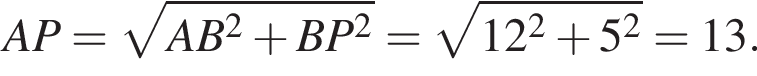

 В прямоугольном треугольнике CHK имеем:
В прямоугольном треугольнике CHK имеем:  Тогда
Тогда  Радиус окружности, описанной вокруг треугольника ABK по теореме синусов
Радиус окружности, описанной вокруг треугольника ABK по теореме синусов
 откуда получаем, что FH = 2DH.
откуда получаем, что FH = 2DH.











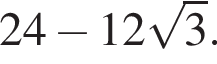





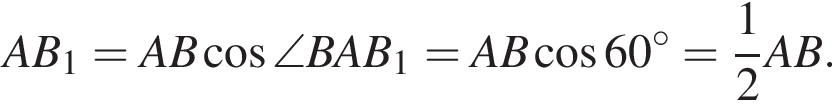
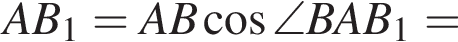




 Треугольники ABC и AB1C1 имеют общий угол A и
Треугольники ABC и AB1C1 имеют общий угол A и  следовательно, они подобны. Тогда
следовательно, они подобны. Тогда  Значит,
Значит,
 откуда
откуда 






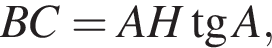 откуда
откуда 
 Тогда для отношения площади треугольника MBK к площади четырёхугольника AKMC получаем:
Тогда для отношения площади треугольника MBK к площади четырёхугольника AKMC получаем:



 Для треугольника ABC справедливо равенство
Для треугольника ABC справедливо равенство  Учитывая, что ∠KHB = ∠BAC, получаем:
Учитывая, что ∠KHB = ∠BAC, получаем:  Стороны BC и BK — сходственные в подобных треугольниках ABC и MBK, следовательно, их коэффициент подобия
Стороны BC и BK — сходственные в подобных треугольниках ABC и MBK, следовательно, их коэффициент подобия 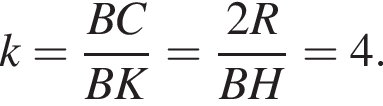 Найдём отношение площади треугольника MBK к площади четырёхугольника AKMC:
Найдём отношение площади треугольника MBK к площади четырёхугольника AKMC:




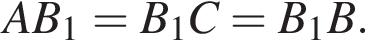 Отрезок
Отрезок  точка
точка  Из рисунка видно, что площадь шестиугольника
Из рисунка видно, что площадь шестиугольника  равна сумме площадей
равна сумме площадей  Поскольку треугольник A1B1C1 подобен треугольнику ABC c коэффициентом подобия
Поскольку треугольник A1B1C1 подобен треугольнику ABC c коэффициентом подобия  Пусть K — точка пересечения медианы AA1 и средней линии B1C1. Медиана и средняя линия делят друг друга пополам, поскольку они являются диагоналями параллелограмма AB1A1C1. Откуда
Пусть K — точка пересечения медианы AA1 и средней линии B1C1. Медиана и средняя линия делят друг друга пополам, поскольку они являются диагоналями параллелограмма AB1A1C1. Откуда 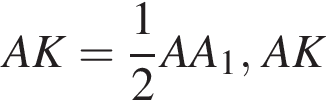 — медиана треугольника AB1C1. Заметим, что
— медиана треугольника AB1C1. Заметим, что 


 Аналогично площади треугольников A1C1B2 и A1B1C2 равны
Аналогично площади треугольников A1C1B2 и A1B1C2 равны 
 Для доказательства на продолжении отрезка AA1 за точку A1 отложим отрезок A1P = AA1. Получим параллелограмм ACPB со сторонами AC = PB = b и AB = CP = c и диагоналями BC = a и AP = 2AA1. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон:
Для доказательства на продолжении отрезка AA1 за точку A1 отложим отрезок A1P = AA1. Получим параллелограмм ACPB со сторонами AC = PB = b и AB = CP = c и диагоналями BC = a и AP = 2AA1. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон:


 а
а  Пусть L — середина отрезка AB1. Поскольку A2 — точка пересечения медиан треугольника AB1C1, она лежит на отрезке C1L и делит его в отношении 2 : 1, считая от точки C1. Значит,
Пусть L — середина отрезка AB1. Поскольку A2 — точка пересечения медиан треугольника AB1C1, она лежит на отрезке C1L и делит его в отношении 2 : 1, считая от точки C1. Значит,  Но треугольники AB1C1 и ABC подобны с коэффициентом 1/2, поэтому
Но треугольники AB1C1 и ABC подобны с коэффициентом 1/2, поэтому  и
и  Повторяя те же рассуждения для треугольника A1B1C получаем, что отрезок A1C2 равен
Повторяя те же рассуждения для треугольника A1B1C получаем, что отрезок A1C2 равен 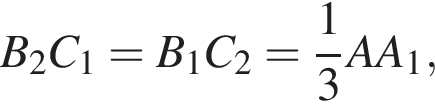
 Следовательно, сумма квадратов сторон шестиугольника равна:
Следовательно, сумма квадратов сторон шестиугольника равна:


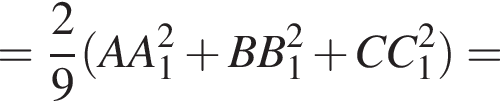

 площади треугольников APR и AQR будут равны друг другу. Из этого следует, что APQR — трапеция. По замечательному свойству трапеции BT делит PQ и AR пополам. Получаем, что
площади треугольников APR и AQR будут равны друг другу. Из этого следует, что APQR — трапеция. По замечательному свойству трапеции BT делит PQ и AR пополам. Получаем, что  и
и  откуда
откуда  Следовательно,
Следовательно,  а значит,
а значит,  Аналогично
Аналогично  Что и требовалось доказать.
Что и требовалось доказать. тогда
тогда  Имеем:
Имеем:





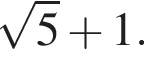
 откуда
откуда  а значит,
а значит,  Следовательно, четырехугольник DCEF вписан в окружность, а тогда
Следовательно, четырехугольник DCEF вписан в окружность, а тогда  Прямые DE и AB параллельны, поэтому
Прямые DE и AB параллельны, поэтому  Треугольник BFE равнобедренный с углом 60°, следовательно, он равносторонний. Что требовалось доказать.
Треугольник BFE равнобедренный с углом 60°, следовательно, он равносторонний. Что требовалось доказать.
 и
и  следовательно,
следовательно,


 и
и  а смежный с ним угол CED равен 60°. Это угол, в свою очередь, является соответственным с углом ABC при параллельных DE и AB и секущей BE. Таким образом, треугольник EFB — равнобедренный с углом 60°, то есть равносторонний.
а смежный с ним угол CED равен 60°. Это угол, в свою очередь, является соответственным с углом ABC при параллельных DE и AB и секущей BE. Таким образом, треугольник EFB — равнобедренный с углом 60°, то есть равносторонний. и
и 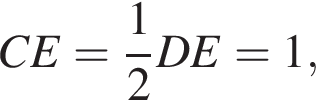 откуда
откуда  Гипотенуза AB вдвое больше средней линии DE, то есть AB = 4. По теореме Пифагора в треугольнике ABC получаем
Гипотенуза AB вдвое больше средней линии DE, то есть AB = 4. По теореме Пифагора в треугольнике ABC получаем  Площадь треугольника равна
Площадь треугольника равна
 Тогда
Тогда  поскольку они опираются на одну дугу KC в окружности, описанной вокруг четырёхугольника AMKC. Кроме того,
поскольку они опираются на одну дугу KC в окружности, описанной вокруг четырёхугольника AMKC. Кроме того,  поскольку они опираются на одну дугу KH в окружности, описанной вокруг четырёхугольника MKHE.
поскольку они опираются на одну дугу KH в окружности, описанной вокруг четырёхугольника MKHE.  поэтому прямые EH и АС параллельны, поскольку это соответственные углы при пересечении EH и AC секущей OA. Это и требовалось доказать.
поэтому прямые EH и АС параллельны, поскольку это соответственные углы при пересечении EH и AC секущей OA. Это и требовалось доказать.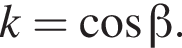 Треугольники OEH и OMK также подобны с тем же коэффициентом подобия. Кроме того, подобны треугольники OMK и AOC, поэтому подобны треугольники OEH и OAC, причем коэффициент подобия равен
Треугольники OEH и OMK также подобны с тем же коэффициентом подобия. Кроме того, подобны треугольники OMK и AOC, поэтому подобны треугольники OEH и OAC, причем коэффициент подобия равен  Тогда
Тогда 




 а
а  значит,
значит,  А это соответственные углы при прямых ЕН и АС и секущей AE. Из равенства этих углов следует параллельность прямых ЕН и АС, что и требовалось доказать.
А это соответственные углы при прямых ЕН и АС и секущей AE. Из равенства этих углов следует параллельность прямых ЕН и АС, что и требовалось доказать.
 (свойство вписанных углов),
(свойство вписанных углов),  (вертикальные). Коэффициент подобия равен
(вертикальные). Коэффициент подобия равен 
 и
и 





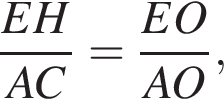 откуда
откуда 
 Аналогично прямая KB параллельна прямой EM, а потому
Аналогично прямая KB параллельна прямой EM, а потому  Следовательно, прямоугольные треугольники CKH и EMA подобны по двум углам, а значит,
Следовательно, прямоугольные треугольники CKH и EMA подобны по двум углам, а значит, 

 Итак, в треугольнике AOC прямые AC и EH делят общий угол AOC, начиная от вершины, на пропорциональные отрезки. Следовательно, по теореме, обратной теореме о пропорциональных отрезках, эти прямые параллельны, что и требовалось доказать.
Итак, в треугольнике AOC прямые AC и EH делят общий угол AOC, начиная от вершины, на пропорциональные отрезки. Следовательно, по теореме, обратной теореме о пропорциональных отрезках, эти прямые параллельны, что и требовалось доказать. и
и  Значит, треугольники MCN и MHN равны по трём сторонам, откуда
Значит, треугольники MCN и MHN равны по трём сторонам, откуда 
 (рис. 2).
(рис. 2).









 и
и 
 и
и 

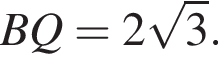 Тогда
Тогда 
 следовательно,
следовательно, 

 В равнобедренном треугольнике MPQ имеем:
В равнобедренном треугольнике MPQ имеем:  Тогда для площади треугольника MPQ получаем:
Тогда для площади треугольника MPQ получаем:


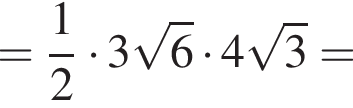




 прямоугольный.
прямоугольный. 





 В каком отношении прямая DL делит сторону AB?
В каком отношении прямая DL делит сторону AB?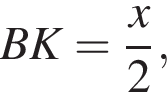
 откуда
откуда 
 поскольку
поскольку  получаем:
получаем:  В пункте а) было доказано, что треугольник LCD равнобедренный, поэтому
В пункте а) было доказано, что треугольник LCD равнобедренный, поэтому 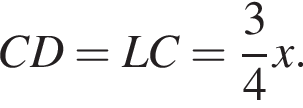 Применим теорему Менелая к треугольнику ABC:
Применим теорему Менелая к треугольнику ABC: 

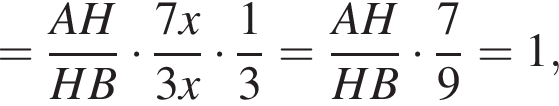
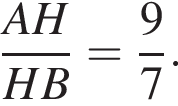
 Тогда
Тогда  как внешний угол треугольника BLD. По теореме синусов для треугольника BHL имеем
как внешний угол треугольника BLD. По теореме синусов для треугольника BHL имеем
 а
а  По теореме синусов для треугольника AHL имеем
По теореме синусов для треугольника AHL имеем




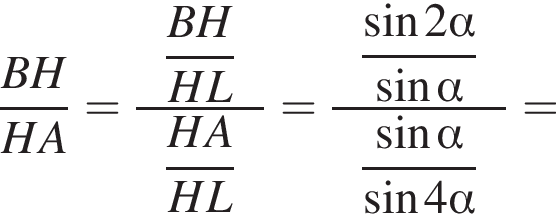



 тогда
тогда 
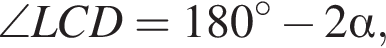
 поэтому
поэтому 
 значит, треугольник LCD равнобедренный.
значит, треугольник LCD равнобедренный.


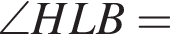

 по двум углам. Отсюда
по двум углам. Отсюда 
 то
то  Пусть BC = x, AB = 3x. По теореме о биссектрисе
Пусть BC = x, AB = 3x. По теореме о биссектрисе  откуда находим
откуда находим 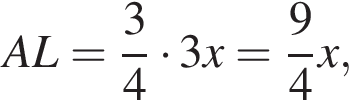
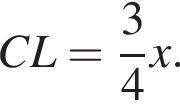 Тогда
Тогда 

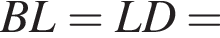

 откуда
откуда 




 Коэффициент подобия треугольников BLC и AML равен
Коэффициент подобия треугольников BLC и AML равен


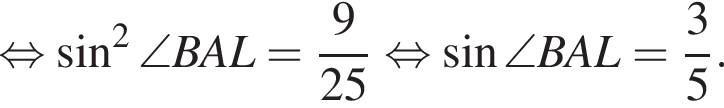


 и площади треугольников AML и BLC относятся как
и площади треугольников AML и BLC относятся как  и
и  Поскольку
Поскольку  находим:
находим: 
 Также имеем
Также имеем  Заметим, что треугольники AB1B и BCB1 имеют общую высоту, следовательно:
Заметим, что треугольники AB1B и BCB1 имеют общую высоту, следовательно:  Поэтому
Поэтому  Аналогично доказываем, что
Аналогично доказываем, что 

 Тогда
Тогда 
 из которого, в свою очередь, следует параллельность отрезков BC и
из которого, в свою очередь, следует параллельность отрезков BC и  в которой точка О — это точка пересечения диагоналей.
в которой точка О — это точка пересечения диагоналей. тогда
тогда 
 составит
составит  в которых
в которых 
 Поэтому площадь
Поэтому площадь  а площадь треугольника
а площадь треугольника  составит его 25-ю часть, то есть
составит его 25-ю часть, то есть  Наконец,
Наконец, 
 то есть DH = 50, тогда HK = 288. Значит,
то есть DH = 50, тогда HK = 288. Значит,  Тогда MH = 120 + 169 = 289.
Тогда MH = 120 + 169 = 289.
 Кроме того,
Кроме того,  Значит, треугольник AME равен треугольнику CMK и тоже прямоугольный, следовательно,
Значит, треугольник AME равен треугольнику CMK и тоже прямоугольный, следовательно,  как угол в прямоугольном треугольнике, лежащий напротив катета, который в два раза меньше гипотенузы.
как угол в прямоугольном треугольнике, лежащий напротив катета, который в два раза меньше гипотенузы.

 а из подобия треугольников CKP и AKT следует, что
а из подобия треугольников CKP и AKT следует, что  Значит, B — середина CP.
Значит, B — середина CP. а так как
а так как  AD — средняя линия треугольника BQP. Значит,
AD — средняя линия треугольника BQP. Значит, 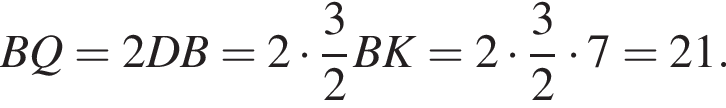







 тогда
тогда  Значит,
Значит,  что и требовалось доказать.
что и требовалось доказать. Значит, точка P имеет координаты (0; 2m). Зная координаты точек, принадлежащих прямым BK и AP, найдём уравнения этих прямых:
Значит, точка P имеет координаты (0; 2m). Зная координаты точек, принадлежащих прямым BK и AP, найдём уравнения этих прямых:


 и Q равно
и Q равно



 Значит, треугольник CMA равнобедренный. Поэтому угол BAC равен углу ACM. Следовательно,
Значит, треугольник CMA равнобедренный. Поэтому угол BAC равен углу ACM. Следовательно,




 то есть
то есть  поэтому
поэтому 
 Отсюда получаем, что
Отсюда получаем, что  Значит,
Значит,  поэтому
поэтому 
 Отсюда получаем, что
Отсюда получаем, что  Значит,
Значит,  поэтому
поэтому 
 и по теореме Пифагора
и по теореме Пифагора  По тереме синусов с учётом свойств вертикальных и смежных углов получаем:
По тереме синусов с учётом свойств вертикальных и смежных углов получаем: 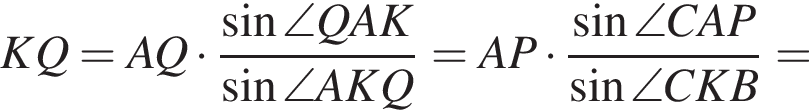








 тогда
тогда 

 Следовательно,
Следовательно, 
 Заметим, что B1O = OB, поскольку треугольник B1OB равнобедренный, и что
Заметим, что B1O = OB, поскольку треугольник B1OB равнобедренный, и что  из треугольника EOB.
из треугольника EOB.
 Далее опустим перпендикуляр OH на сторону BC. Тогда
Далее опустим перпендикуляр OH на сторону BC. Тогда  как радиус вписанной окружности. Тогда
как радиус вписанной окружности. Тогда 

 откуда
откуда 



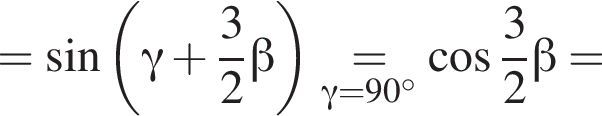



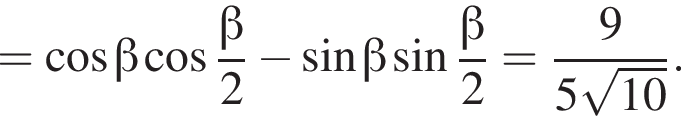





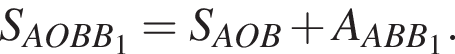 Причём
Причём  где r — радиус окружности, вписанный в треугольник ABC. Для сторон треугольника ABC выполнено соотношение
где r — радиус окружности, вписанный в треугольник ABC. Для сторон треугольника ABC выполнено соотношение  следовательно, угол C прямой. Тогда
следовательно, угол C прямой. Тогда













 и
и 

 Сторону AC найдём по теореме косинусов:
Сторону AC найдём по теореме косинусов: 






 сумма прямых углов
сумма прямых углов  и
и  Углы
Углы 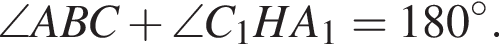 Таким образом, тупой угол между высотами дополняет угол между сторонами, к которым они проведены, до 180°.
Таким образом, тупой угол между высотами дополняет угол между сторонами, к которым они проведены, до 180°. откуда
откуда  Для остроугольного треугольника доказательство аналогично. Для прямоугольного треугольника доказательство напрямую следует из определения котангенса.
Для остроугольного треугольника доказательство аналогично. Для прямоугольного треугольника доказательство напрямую следует из определения котангенса. Теперь по теореме Пифагора вычисляем:
Теперь по теореме Пифагора вычисляем: 


 откуда получаем:
откуда получаем:  (это же следует из подобия треугольников
(это же следует из подобия треугольников 





 тогда в прямоугольном треугольнике BA1C имеем:
тогда в прямоугольном треугольнике BA1C имеем: 
 тогда
тогда
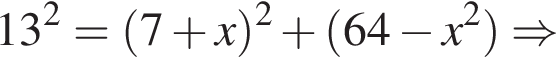

 и
и 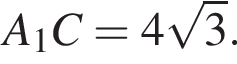












 тогда
тогда 

 откуда
откуда 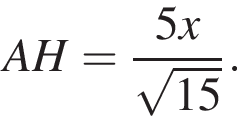 Тогда
Тогда  Но AB и есть диаметр описанной окружности треугольника
Но AB и есть диаметр описанной окружности треугольника 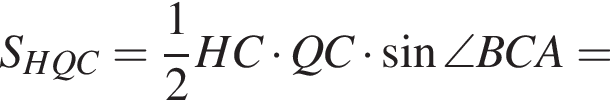
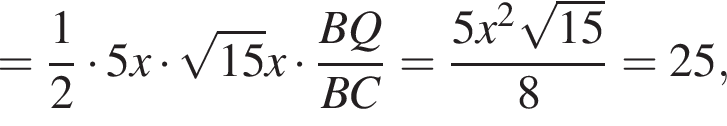
 и
и 

 Если
Если  то
то  Если же
Если же  то образуются треугольники BCD и GCA, которые равны по двум сторонам (
то образуются треугольники BCD и GCA, которые равны по двум сторонам (
 ) и углу между ними:
) и углу между ними:





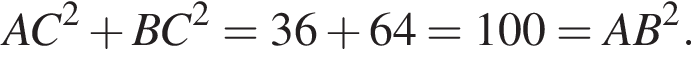

 где
где  Поэтому
Поэтому 
 и
и  Отрезки CP и CQ — биссектрисы треугольников ACB и NCM соответственно.
Отрезки CP и CQ — биссектрисы треугольников ACB и NCM соответственно. а
а 
 Прямая CQ — биссектриса угла NCM, поэтому
Прямая CQ — биссектриса угла NCM, поэтому  Следовательно,
Следовательно,  Что и требовалось доказать.
Что и требовалось доказать. с помощью формулы площади как половины произведения сторон на синус угла между ними:
с помощью формулы площади как половины произведения сторон на синус угла между ними:  тогда
тогда  Аналогично
Аналогично 

 и
и 

 четырехугольник BNPM — ромб. Значит, прямая PM параллельна прямой BC, а поскольку CP — медиана прямоугольного треугольника KCN, проведенная из вершины прямого угла, то
четырехугольник BNPM — ромб. Значит, прямая PM параллельна прямой BC, а поскольку CP — медиана прямоугольного треугольника KCN, проведенная из вершины прямого угла, то  Следовательно, четырехугольник BCPM — равнобедренная трапеция.
Следовательно, четырехугольник BCPM — равнобедренная трапеция. треугольник CPM равнобедренный, поэтому
треугольник CPM равнобедренный, поэтому 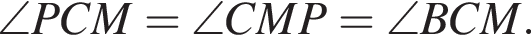 Значит, CM — биссектриса угла BCP. Тогда
Значит, CM — биссектриса угла BCP. Тогда 
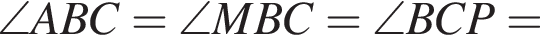



















 Имеем:
Имеем:  следовательно, треугольники
следовательно, треугольники  и
и  Но по условию
Но по условию  поэтому отрезки
поэтому отрезки  — параллелограмм по признаку параллелограмма.
— параллелограмм по признаку параллелограмма.
 а тогда
а тогда  По теореме Пифагора в треугольнике AQC имеем:
По теореме Пифагора в треугольнике AQC имеем:  По теореме Менелая
По теореме Менелая 
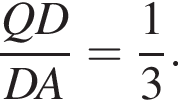 Тогда
Тогда  и по теореме Пифагора для треугольника DQC находим
и по теореме Пифагора для треугольника DQC находим 
 Пусть
Пусть 
 тогда из полученного соотношения находим, что
тогда из полученного соотношения находим, что  Снова применим обобщенную теорему Фалеса — для отрезков
Снова применим обобщенную теорему Фалеса — для отрезков  и параллельных прямых
и параллельных прямых Получим:
Получим:  Значит, точка D делит отрезок BB1 так же, как точка А1 делит ВС. По теореме, обратной обобщенной теореме Фалеса, из этого следует параллельность прямых DA1 и B1C, а также подобие треугольников BDA1 и BB1C.
Значит, точка D делит отрезок BB1 так же, как точка А1 делит ВС. По теореме, обратной обобщенной теореме Фалеса, из этого следует параллельность прямых DA1 и B1C, а также подобие треугольников BDA1 и BB1C. Но по условию
Но по условию  следовательно,
следовательно,  Таким образом, противоположные стороны
Таким образом, противоположные стороны 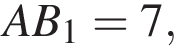
 Четырехугольник
Четырехугольник  По теореме Фалеса для отрезков
По теореме Фалеса для отрезков  откуда
откуда 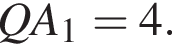 По теореме Пифагора в прямоугольном треугольнике
По теореме Пифагора в прямоугольном треугольнике  По теореме Пифагора в треугольнике DQC вычисляем
По теореме Пифагора в треугольнике DQC вычисляем 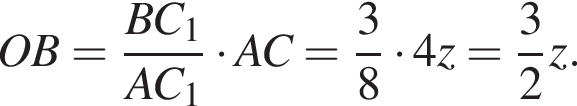

 откуда
откуда  то есть противоположные стороны
то есть противоположные стороны  прямоугольный с гипотенузой
прямоугольный с гипотенузой  и катетом
и катетом  а потому
а потому  Сумма углов, прилежащих к боковой стороне трапеции, равна 180°, поэтому
Сумма углов, прилежащих к боковой стороне трапеции, равна 180°, поэтому 





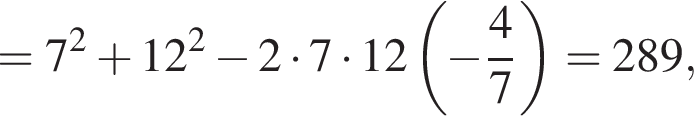




 Получаем:
Получаем:











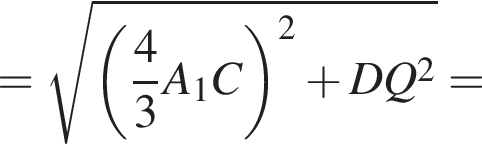
 В треугольнике ABC медиана AA1 является высотой, значит, треугольник ABC является равнобедренным и AB = AC.
В треугольнике ABC медиана AA1 является высотой, значит, треугольник ABC является равнобедренным и AB = AC.





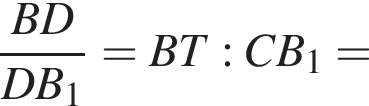
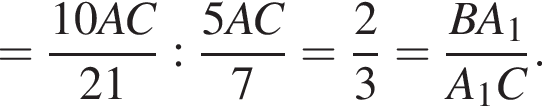
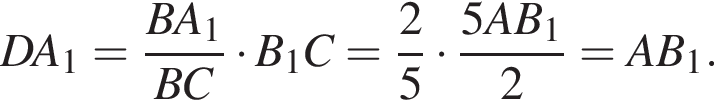

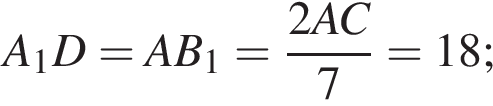



 C1A1 — медиана в прямоугольном треугольнике BC1C, поэтому
C1A1 — медиана в прямоугольном треугольнике BC1C, поэтому





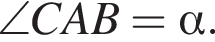 Треугольник ANC равнобедренный, поэтому
Треугольник ANC равнобедренный, поэтому  и
и  Треугольник CLN также равнобедренный, поэтому
Треугольник CLN также равнобедренный, поэтому Вычислим
Вычислим  как внешний угол в треугольнике LMC:
как внешний угол в треугольнике LMC:



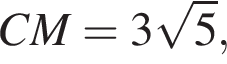

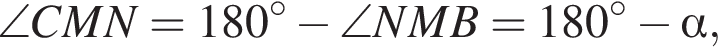









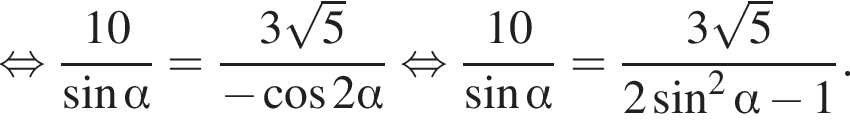


 тогда
тогда


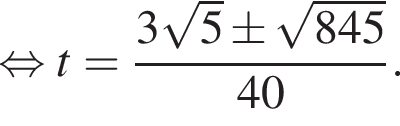
 поэтому
поэтому 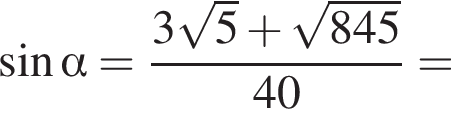






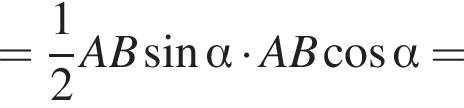

 поэтому дуга AL равна 90°. На эту дугу опирается центральный угол ANL, тогда
поэтому дуга AL равна 90°. На эту дугу опирается центральный угол ANL, тогда  Углы ANL и MNB равны как вертикальные, таким образом,
Углы ANL и MNB равны как вертикальные, таким образом,  тогда треугольники ABC и MNB подобны по двум углам. Следовательно,
тогда треугольники ABC и MNB подобны по двум углам. Следовательно, 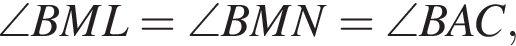 что и требовалось доказать.
что и требовалось доказать.



 тогда
тогда 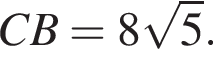















 то есть ALM — равнобедренный прямоугольный треугольник. Значит,
то есть ALM — равнобедренный прямоугольный треугольник. Значит,





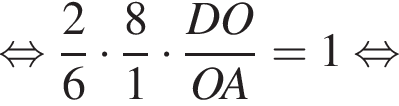
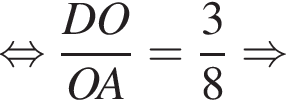




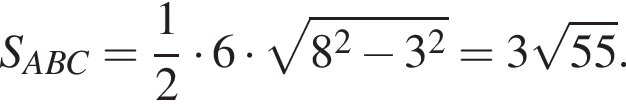



 Имеем:
Имеем: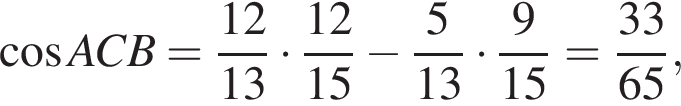












 По теореме о внешнем угле треугольника
По теореме о внешнем угле треугольника  Треугольник ABD равнобедренный, поэтому
Треугольник ABD равнобедренный, поэтому 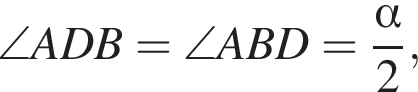 а так как AM параллельна BD,
а так как AM параллельна BD,
 значит,
значит,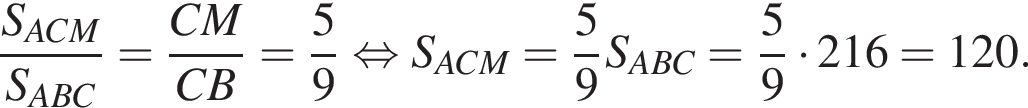






 BE : EC = 10 : 1, а треугольник AEF является равносторонним.
BE : EC = 10 : 1, а треугольник AEF является равносторонним. 
 поэтому
поэтому 






 значит,
значит, 
 то есть
то есть  Окончательно получаем уравнение
Окончательно получаем уравнение 
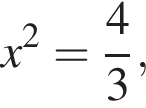 поэтому
поэтому  Для получения ответа заметим, что площадь равностороннего треугольника со стороной z равна
Для получения ответа заметим, что площадь равностороннего треугольника со стороной z равна 
 Пусть
Пусть  тогда
тогда


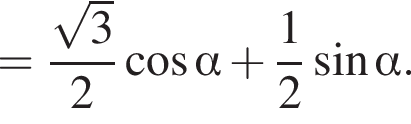








 Из прямоугольного треугольника AFP получим
Из прямоугольного треугольника AFP получим 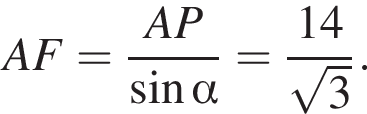

 Такая же величина у вертикального к нему угла LIK. По условию около четырёхугольника CKIL можно описать окружность. Следовательно, угол BCA дополняет угол LIK до 180°. С другой стороны, по теореме о сумме углов треугольника угол BCA дополняет до 180° сумму углов
Такая же величина у вертикального к нему угла LIK. По условию около четырёхугольника CKIL можно описать окружность. Следовательно, угол BCA дополняет угол LIK до 180°. С другой стороны, по теореме о сумме углов треугольника угол BCA дополняет до 180° сумму углов  и
и  Значит, угол BCA равен 60°.
Значит, угол BCA равен 60°. Площадь треугольника ABC равна половине произведения его периметра на радиус вписанной окружности. Значит, эта площадь равна
Площадь треугольника ABC равна половине произведения его периметра на радиус вписанной окружности. Значит, эта площадь равна 
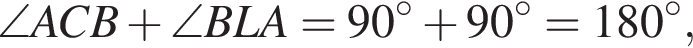

 и
и 




 следовательно,
следовательно,


 аналогично
аналогично 



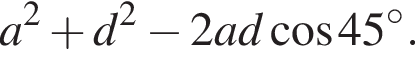

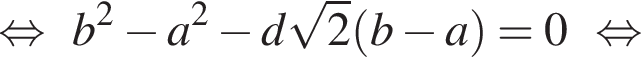

 либо a = b, тогда треугольник ABC равнобедренный, и
либо a = b, тогда треугольник ABC равнобедренный, и 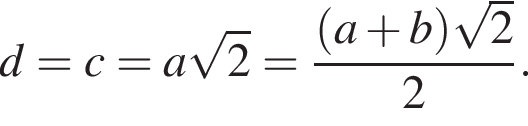



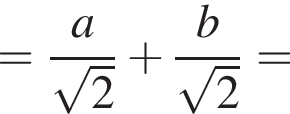


 и
и 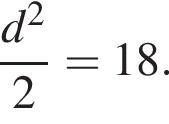
 как вписанные, следовательно,
как вписанные, следовательно,  откуда
откуда  Что требовалось доказать.
Что требовалось доказать.




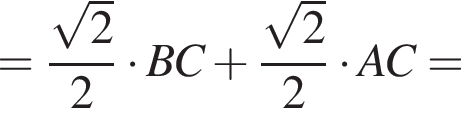










 что и требовалось доказать.
что и требовалось доказать.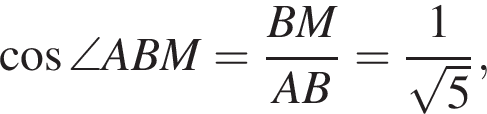

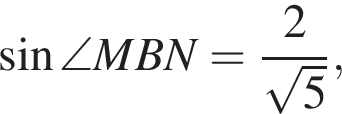 откуда
откуда
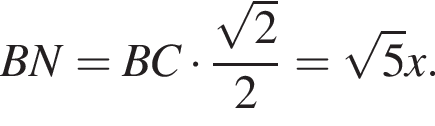
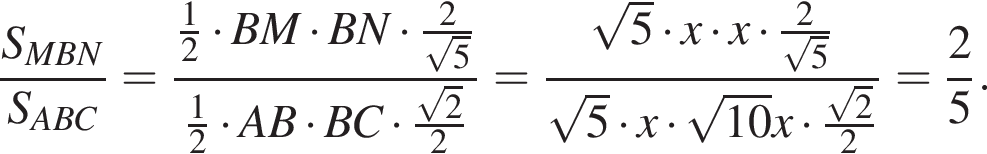



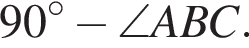 Таким образом, треугольники HMN и CAB подобны по двум углам. Это и требовалось доказать.
Таким образом, треугольники HMN и CAB подобны по двум углам. Это и требовалось доказать.
 Тогда треугольники CMH и BNH подобны по двум углам, причем из пункта а) следует, что
Тогда треугольники CMH и BNH подобны по двум углам, причем из пункта а) следует, что
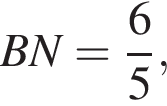 а тогда
а тогда 
 Аналогично, по свойству биссектрисы, только для треугольника ABH получаем:
Аналогично, по свойству биссектрисы, только для треугольника ABH получаем: 


 Тогда треугольники AFG и AHD подобны по двум сторонам и углу между ними. Значит, прямые FG и HD параллельны, то есть прямые FG и BC параллельны. Что и требовалось доказать.
Тогда треугольники AFG и AHD подобны по двум сторонам и углу между ними. Значит, прямые FG и HD параллельны, то есть прямые FG и BC параллельны. Что и требовалось доказать.

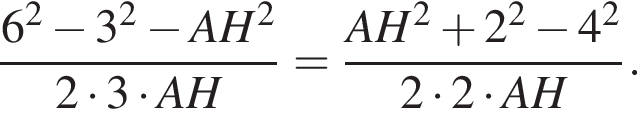



 а точка B лежит между C и P.
а точка B лежит между C и P. Теперь получаем, что угол PBB1 равен
Теперь получаем, что угол PBB1 равен  Угол ABB1 же тогда равен
Угол ABB1 же тогда равен  откуда
откуда 

 Диаметры описанных окружностей подобных треугольников относятся как коэффициент подобия, поэтому
Диаметры описанных окружностей подобных треугольников относятся как коэффициент подобия, поэтому  Отсюда AH = 6.
Отсюда AH = 6.
 поэтому треугольники AFH и BFC подобны по двум углам. Из подобия следует равенство:
поэтому треугольники AFH и BFC подобны по двум углам. Из подобия следует равенство: 


 Отсюда
Отсюда 

 Что и требовалось доказать.
Что и требовалось доказать.




 Что и требовалось доказать.
Что и требовалось доказать. найдем
найдем 

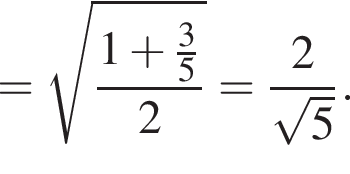

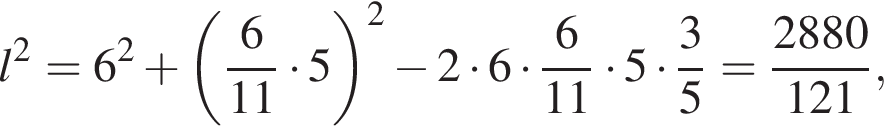
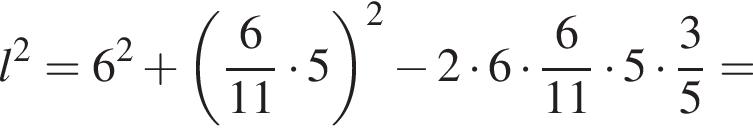

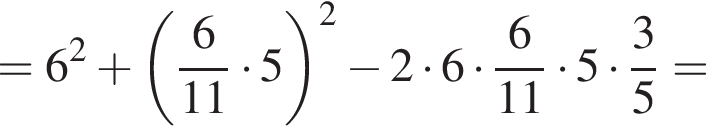
 Теперь, по свойству биссектрисы, получаем, что
Теперь, по свойству биссектрисы, получаем, что  Отсюда
Отсюда 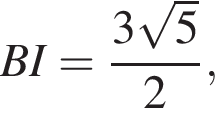 а тогда
а тогда 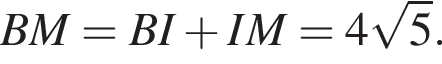
 поскольку CN — биссектриса, следовательно,
поскольку CN — биссектриса, следовательно, 
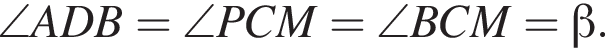
 по свойству вертикальных углов, треугольники APD и МРС подобны, поэтому ∠PMC = 90°. Таким образом, в треугольнике ВСР биссектриса СМ является высотой, а значит, треугольник ВСР равнобедренный и PM = MB, CP = CB.
по свойству вертикальных углов, треугольники APD и МРС подобны, поэтому ∠PMC = 90°. Таким образом, в треугольнике ВСР биссектриса СМ является высотой, а значит, треугольник ВСР равнобедренный и PM = MB, CP = CB.
 следует, что ∠PCD = ∠PDC. Поэтому треугольник PCD равнобедренный и PD = PC. Значит, треугольники APD и МРС равны, поэтому
следует, что ∠PCD = ∠PDC. Поэтому треугольник PCD равнобедренный и PD = PC. Значит, треугольники APD и МРС равны, поэтому  откуда следует, что BP = 2AP.
откуда следует, что BP = 2AP. Отсюда следует, что треугольник ВСР равносторонний, поэтому ∠BPC = 60°. Из равенства
Отсюда следует, что треугольник ВСР равносторонний, поэтому ∠BPC = 60°. Из равенства  получаем, что AP = 2 и
получаем, что AP = 2 и  Теперь найдём площадь четырёхугольника AВCD:
Теперь найдём площадь четырёхугольника AВCD:


 следовательно,
следовательно, 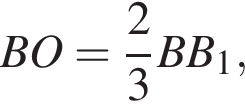
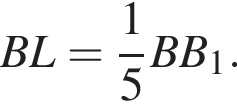 Отсюда
Отсюда 
 Тогда:
Тогда:
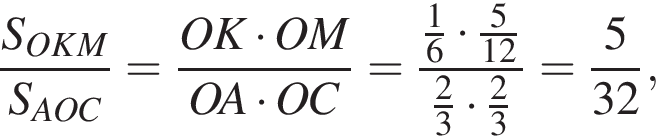









 Значит,
Значит, 
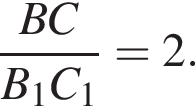 С другой стороны, коэффициент подобия равен
С другой стороны, коэффициент подобия равен  Отсюда
Отсюда 
 Тогда
Тогда  Пусть AA1 и B1C1 пересекаются в точке D. Запишем две теоремы синусов — для треугольников AB1D и AC1D:
Пусть AA1 и B1C1 пересекаются в точке D. Запишем две теоремы синусов — для треугольников AB1D и AC1D:






 По свойству биссектрисы,
По свойству биссектрисы,  тогда
тогда




 Окружность, вписанная в треугольник ABC, касается отрезка MN в точке K.
Окружность, вписанная в треугольник ABC, касается отрезка MN в точке K.
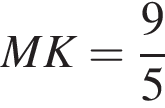 и
и 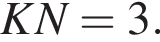
 MN = 3t, AC = 5t. По свойству описанного четырёхугольника,
MN = 3t, AC = 5t. По свойству описанного четырёхугольника, 


 Что и требовалось доказать.
Что и требовалось доказать.

 По теореме Пифагора
По теореме Пифагора 


 тогда радиус окружности, вписанной в треугольник ABC, равен 3.
тогда радиус окружности, вписанной в треугольник ABC, равен 3.




 Решая систему уравнений, получим AB = 17, BC = 15.
Решая систему уравнений, получим AB = 17, BC = 15. следовательно, он прямоугольный, и его площадь равна
следовательно, он прямоугольный, и его площадь равна  С другой стороны,
С другой стороны, 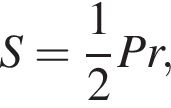 тогда
тогда
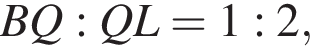 а
а  M — точка пересечения медиан.
M — точка пересечения медиан.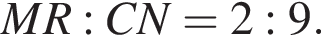
 Пусть
Пусть 
 Тогда из условия следует, что
Тогда из условия следует, что 
 Отсюда
Отсюда  Что и следовало доказать.
Что и следовало доказать.

 Медианы делят треугольник на шесть равновеликих треугольников, поэтому площади треугольников ABM, ACM, BCM равны 2 каждая. Тогда
Медианы делят треугольник на шесть равновеликих треугольников, поэтому площади треугольников ABM, ACM, BCM равны 2 каждая. Тогда 









 и
и 

 Тогда
Тогда 

 следовательно,
следовательно,  Равные дуги стягивают равные хорды, следовательно, BM = CN.
Равные дуги стягивают равные хорды, следовательно, BM = CN. таким образом, треугольник BDN равнобедренный,
таким образом, треугольник BDN равнобедренный,  Тогда, как гипотенуза в прямоугольном треугольнике BHD с углом 30 градусов BD = ND = 2BH = 14.
Тогда, как гипотенуза в прямоугольном треугольнике BHD с углом 30 градусов BD = ND = 2BH = 14. 

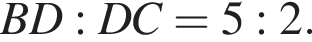
 По свойству биссектрисы треугольника
По свойству биссектрисы треугольника  Значит,
Значит,  что и требовалось доказать.
что и требовалось доказать. а
а  тогда
тогда  Треугольники BDE и CDK подобны по двум углам (
Треугольники BDE и CDK подобны по двум углам ( как вертикальные,
как вертикальные,  ), треугольники AEF и AKC подобны по двум углам (угол A — общий,
), треугольники AEF и AKC подобны по двум углам (угол A — общий,  ). Пусть
). Пусть  а
а  тогда
тогда 

 Тогда
Тогда



 Отрезок BF пересекает отрезок MN в точке E. Найдите радиус окружности, описанной около четырёхугольника AMNC, если
Отрезок BF пересекает отрезок MN в точке E. Найдите радиус окружности, описанной около четырёхугольника AMNC, если  и
и 
 Поскольку окружность можно описать только около равнобедренной трапеции,
Поскольку окружность можно описать только около равнобедренной трапеции,  то есть
то есть  а значит, треугольник ABC равнобедренный.
а значит, треугольник ABC равнобедренный. Поскольку отрезок MN — средняя линия треугольника ABC, он делит высоту BH пополам, значит,
Поскольку отрезок MN — средняя линия треугольника ABC, он делит высоту BH пополам, значит,  Треугольник ABC равнобедренный, поэтому
Треугольник ABC равнобедренный, поэтому 




 точка H лежит на прямой BO, а NO — радиус окружности, описанной около четырёхугольника AMNC.
точка H лежит на прямой BO, а NO — радиус окружности, описанной около четырёхугольника AMNC.
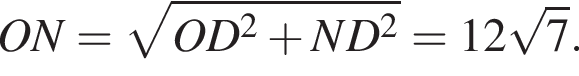





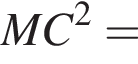





 и
и 

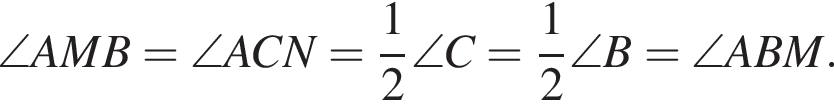


 Высота этого треугольника, проведенная из вершины C, равна высоте треугольника ABC, приведённой из вершины A, то есть
Высота этого треугольника, проведенная из вершины C, равна высоте треугольника ABC, приведённой из вершины A, то есть 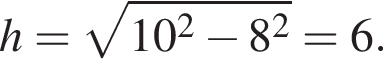 Поэтому из пропорции
Поэтому из пропорции  получаем
получаем

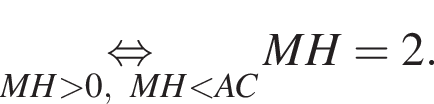
 а потому
а потому 
 взята точка D так, что
взята точка D так, что  Биссектриса BL пересекает отрезок AD в точке P, отрезок CK — перпендикуляр к прямой AD.
Биссектриса BL пересекает отрезок AD в точке P, отрезок CK — перпендикуляр к прямой AD.

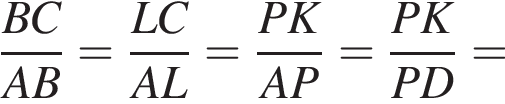
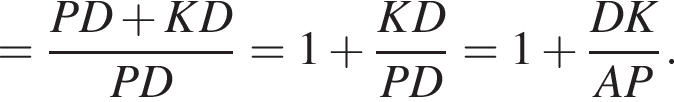




 то есть
то есть  Следовательно,
Следовательно,
 И поскольку
И поскольку  находим:
находим:
 и
и 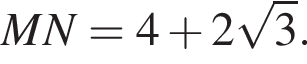
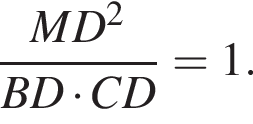
 Поэтому треугольники BMD и MCD подобны по двум углам, значит,
Поэтому треугольники BMD и MCD подобны по двум углам, значит,  откуда
откуда 
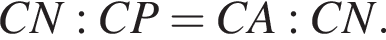 Отсюда следует, что
Отсюда следует, что  Из подобия треугольников CMD и CBM получаем, что
Из подобия треугольников CMD и CBM получаем, что  а потому
а потому  Из подобия треугольников CPB и CDA получаем, что
Из подобия треугольников CPB и CDA получаем, что  откуда следует, что
откуда следует, что  Таким образом,
Таким образом,  или
или 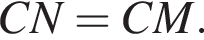 Следовательно, отрезок CL — биссектриса и высота треугольника CMN.
Следовательно, отрезок CL — биссектриса и высота треугольника CMN. тогда по теореме косинусов получаем
тогда по теореме косинусов получаем




 то есть
то есть








 представляет собой известное соотношение: высота прямоугольного треугольника, проведенная из вершины прямого угла, является средним пропорциональным между проекциями катетов на гипотенузу.
представляет собой известное соотношение: высота прямоугольного треугольника, проведенная из вершины прямого угла, является средним пропорциональным между проекциями катетов на гипотенузу.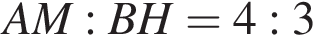 и MH = 3.
и MH = 3. значит,
значит,  откуда следует, что отрезок AM — медиана и высота, следовательно,
откуда следует, что отрезок AM — медиана и высота, следовательно, 
 то есть BC = 6. Пусть
то есть BC = 6. Пусть  и
и  тогда
тогда
 Следовательно,
Следовательно,  откуда для площади треугольника ABC получаем:
откуда для площади треугольника ABC получаем:
 и
и  Заметим, что
Заметим, что 



 или
или  Значит,
Значит, 

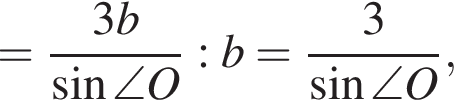





 поэтому
поэтому 


 Что и требовалось доказать.
Что и требовалось доказать.
 тогда
тогда  и
и  Следовательно, треугольник KLN равнобедренный, а отрезок LM — его высота и биссектриса. По доказанному ранее отрезок MC — биссектриса треугольника LMN, поэтому
Следовательно, треугольник KLN равнобедренный, а отрезок LM — его высота и биссектриса. По доказанному ранее отрезок MC — биссектриса треугольника LMN, поэтому 




 Из подобия треугольников A1BN и A1CA получим, что
Из подобия треугольников A1BN и A1CA получим, что  Из подобия треугольников B1PC и BPM получим, что
Из подобия треугольников B1PC и BPM получим, что  Аналогично
Аналогично 


 откуда
откуда  Далее, по теореме Менелая для треугольника ABA1 и секущей PC получим:
Далее, по теореме Менелая для треугольника ABA1 и секущей PC получим:
 то есть
то есть 


 AB = 7 и AC = 10.
AB = 7 и AC = 10. Тогда
Тогда 
 По условию
По условию  значит,
значит,

 Следовательно,
Следовательно, 



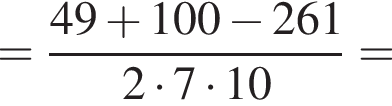






 следовательно,
следовательно, 
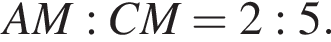
 Пусть
Пусть 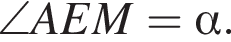 Тогда
Тогда 
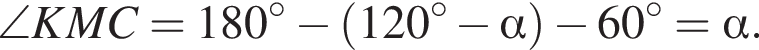


 и
и  По теореме косинусов:
По теореме косинусов:







 и
и  Отсюда
Отсюда 
 угол ABC прямой, значит,
угол ABC прямой, значит,

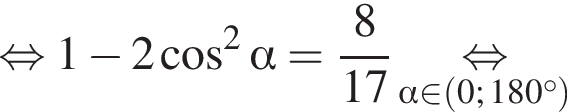









 значит, по обратной теореме Пифагора, треугольник ABC прямоугольный. Введем систему координат с началом в точке B, как показано на рисунке. В этой системе координат имеем:
значит, по обратной теореме Пифагора, треугольник ABC прямоугольный. Введем систему координат с началом в точке B, как показано на рисунке. В этой системе координат имеем:




 Найдем координаты точки B1:
Найдем координаты точки B1:






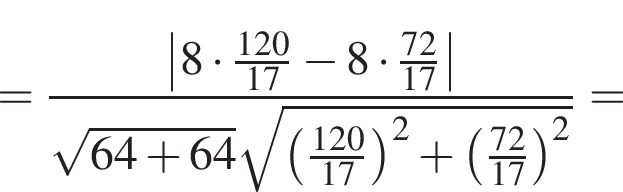



 угол A равен 60°. Точка D — точка пересечения биссектрис, точка Н — точка пересечения высот.
угол A равен 60°. Точка D — точка пересечения биссектрис, точка Н — точка пересечения высот.






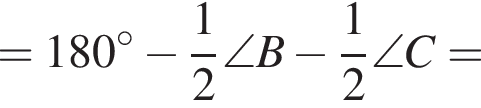
 следовательно, точки B, H, D, C лежат на одной окружности.
следовательно, точки B, H, D, C лежат на одной окружности. тогда
тогда  Значит,
Значит, 





 откуда
откуда 


 и
и 
















 Что и требовалось доказать.
Что и требовалось доказать.

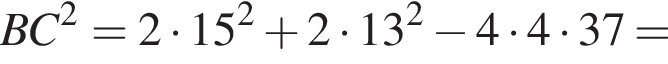







 то есть
то есть  Используя результат пункта a), получаем, что
Используя результат пункта a), получаем, что 


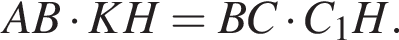

 и
и 
 откуда находим:
откуда находим: 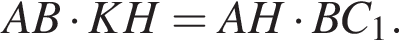 Из равенства углов
Из равенства углов  следует подобие треугольников BCC1 и HAC1, откуда находим:
следует подобие треугольников BCC1 и HAC1, откуда находим:




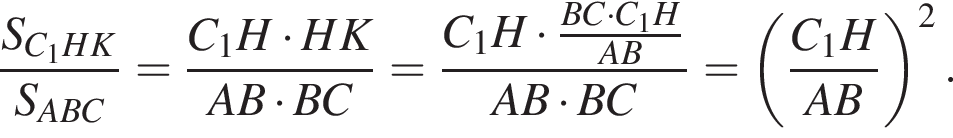



 Получаем:
Получаем: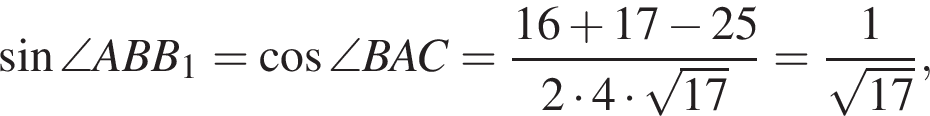



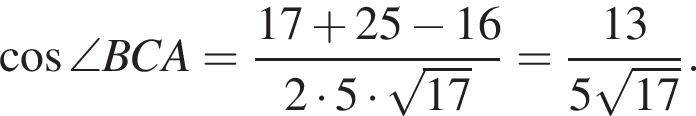






 и
и  В треугольник MNK вписан квадрат, две вершины которого лежат на стороне MN, одна на стороне NK и одна на стороне MK. Через середину стороны MN и центр квадрата проведена прямая, которая пресекается с высотой KH в точке O, а с прямой NK — в точке F.
В треугольник MNK вписан квадрат, две вершины которого лежат на стороне MN, одна на стороне NK и одна на стороне MK. Через середину стороны MN и центр квадрата проведена прямая, которая пресекается с высотой KH в точке O, а с прямой NK — в точке F.
 Из подобия треугольников MNK и DCK получаем, что
Из подобия треугольников MNK и DCK получаем, что 






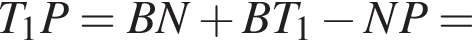








 откуда
откуда






 Точка D лежит на стороне FH, A и B — точки пересечения медиан треугольников FGD и DGH соответственно.
Точка D лежит на стороне FH, A и B — точки пересечения медиан треугольников FGD и DGH соответственно.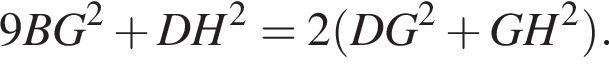







 поэтому
поэтому



 поскольку
поскольку  а высота, проведенная из точки G, — общая. Далее,
а высота, проведенная из точки G, — общая. Далее, 


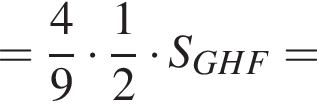
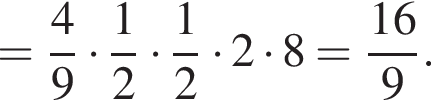
 и
и  отмечены точки E и D соответственно так, что
отмечены точки E и D соответственно так, что 
 Отрезки AD и CE пересекаются в точке O.
Отрезки AD и CE пересекаются в точке O.
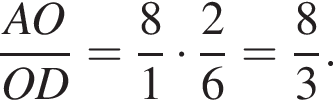 Запишем теорему Менелая для треугольника CBE и секущей DO:
Запишем теорему Менелая для треугольника CBE и секущей DO:
 Таким образом, отношение площадей треугольников AOE и COD равно
Таким образом, отношение площадей треугольников AOE и COD равно




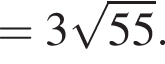




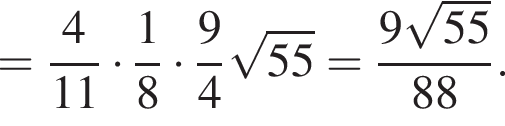


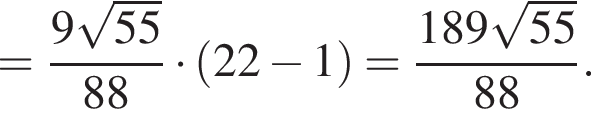

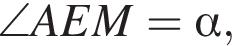 тогда
тогда  Треугольники BEK и MEK равны, поскольку они симметричны относительно EK. Тогда
Треугольники BEK и MEK равны, поскольку они симметричны относительно EK. Тогда  и
и 
 Пусть также CK = t, тогда
Пусть также CK = t, тогда  Из подобия треугольников AME и CKM находим:
Из подобия треугольников AME и CKM находим:


 следовательно,
следовательно, 







 Далее,
Далее,
 следовательно,
следовательно,

 тогда
тогда  По свойству прямоугольного треугольника
По свойству прямоугольного треугольника  Треугольник CHB прямоугольный,
Треугольник CHB прямоугольный,  тогда
тогда 
 поэтому в треугольнике ACK имеем
поэтому в треугольнике ACK имеем  тогда прямые AM и CN перпендикулярны.
тогда прямые AM и CN перпендикулярны.
 откуда AH = AQ и AC = 2AQ. Далее, AQ = QC, а из равных прямоугольных треугольников AQM и CQM находим: AM = MC. Получаем, что отрезок AM — медиана, равная половине стороны, к которой проведена. Из этого следует, что при вершине A треугольника ABC расположен прямой угол.
откуда AH = AQ и AC = 2AQ. Далее, AQ = QC, а из равных прямоугольных треугольников AQM и CQM находим: AM = MC. Получаем, что отрезок AM — медиана, равная половине стороны, к которой проведена. Из этого следует, что при вершине A треугольника ABC расположен прямой угол. откуда
откуда






 а потому смежный с ним
а потому смежный с ним  В четырехугольнике AQMH сумма градусных мер противолежащих углов равна 180°, значит, он вписанный. Отсюда
В четырехугольнике AQMH сумма градусных мер противолежащих углов равна 180°, значит, он вписанный. Отсюда  и, как следствие,
и, как следствие,  Из равных прямоугольных треугольников AQM и CQM находим AM = MC. Получаем, что отрезок AM — медиана, равная половине стороны, к которой проведена. Из этого следует, что при вершине A треугольника ABC расположен прямой угол.
Из равных прямоугольных треугольников AQM и CQM находим AM = MC. Получаем, что отрезок AM — медиана, равная половине стороны, к которой проведена. Из этого следует, что при вершине A треугольника ABC расположен прямой угол. значит,
значит,  Далее
Далее  как вертикальные углы, откуда в прямоугольном треугольнике FHM получаем
как вертикальные углы, откуда в прямоугольном треугольнике FHM получаем  и
и  Следовательно,
Следовательно,  и
и

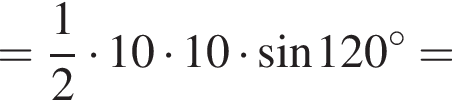
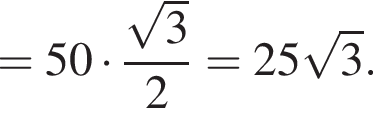


 Треугольник BMN — равнобедренный по определению, поэтому
Треугольник BMN — равнобедренный по определению, поэтому  Значит,
Значит,  треугольник OMN — равнобедренный, то есть
треугольник OMN — равнобедренный, то есть  Следовательно, треугольники MBO и NBO равны по трем сторонам, откуда
Следовательно, треугольники MBO и NBO равны по трем сторонам, откуда  Таким образом, луч BP — биссектриса угла ABC.
Таким образом, луч BP — биссектриса угла ABC.


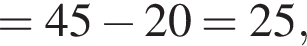



 Тогда по теореме косинусов в треугольнике ABP:
Тогда по теореме косинусов в треугольнике ABP: