1. Тип 18 № 509506 

Источники:
Классификатор алгебры: Комбинация прямых
Методы алгебры: Группировка
Задача с параметром. Системы с параметром
i
Найдите все значения a, при каждом из которых система уравнений

имеет ровно два различных решения.
Решение. Заметим, что





Поэтому исходная система равносильна смешанной системе

Полученная смешанная система имеет ровно два решения в том и только в том случае, когда прямые  имеет с графиком системы
имеет с графиком системы

ровно две общие точки. Прямые, соответствующие границам этих случаев, пронумерованы на рисунке числами от 1 до 5. Искомыми значениями параметра являются 
Ответ: 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен правильный ответ | 4 |
| Найдено множество значений a, корни, соответствующие единственному значению параметра не определены ИЛИ Найдены корни, но в множество значений a не включены одна или две граничные точки | 3 |
| Найдено множество значений a, но не включены одна или две граничные точки. Корни, соответствующие единственному значению параметра не найдены | 2 |
| Верно найдена хотя бы одна граничная точка искомого множества значений a | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
Ответ: 

509506


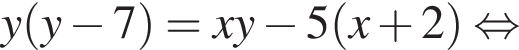




 имеет единственную общую точку с объединением двух лучей
имеет единственную общую точку с объединением двух лучей  при условиях
при условиях  (см. рис.).
(см. рис.).








 поэтому при
поэтому при  корней нет, при
корней нет, при  получаем один корень
получаем один корень  при
при  получаем два различных корня. У параболы
получаем два различных корня. У параболы  — ветви вверх, абсцисса вершины равна
— ветви вверх, абсцисса вершины равна 
 то есть при
то есть при  а при
а при  один корень меньше −3, а другой — больше −3.
один корень меньше −3, а другой — больше −3.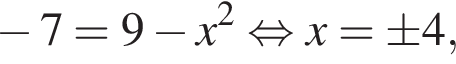 с учётом
с учётом  из
из  получаем, что x = 4, a = −3.
получаем, что x = 4, a = −3.

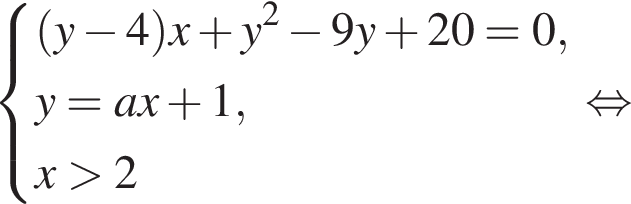


 задает пару пересекающихся прямых
задает пару пересекающихся прямых 

 задает прямую m с угловым коэффициентом a, проходящую через точку
задает прямую m с угловым коэффициентом a, проходящую через точку  Следует найти все значения a, при каждом из которых прямая m имеет единственную общую точку с объединением лучей BD и
Следует найти все значения a, при каждом из которых прямая m имеет единственную общую точку с объединением лучей BD и  Поэтому при
Поэтому при 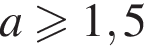 прямая m не пересечет ни луч BD, ни луч
прямая m не пересечет ни луч BD, ни луч  Поэтому при
Поэтому при 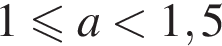 прямая m пересечет луч BD, но не пересечет луч
прямая m пересечет луч BD, но не пересечет луч  прямая m пресечет и луч BD, и луч
прямая m пресечет и луч BD, и луч  прямая m пересечет только луч CE, а при
прямая m пересечет только луч CE, а при  она не пересечет ни луч BD, ни луч
она не пересечет ни луч BD, ни луч 
 имеет ровно два решения.
имеет ровно два решения. то она имеет и решения
то она имеет и решения 
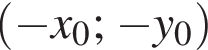 и
и  Чтобы система имела ровно два решения, какие-то из пар должны совпадать.
Чтобы система имела ровно два решения, какие-то из пар должны совпадать.  и
и  а второе принимает вид
а второе принимает вид 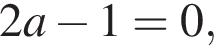 что невозможно одновременно.
что невозможно одновременно.  то первое уравнение системы принимает вид
то первое уравнение системы принимает вид  а второе принимает вид
а второе принимает вид 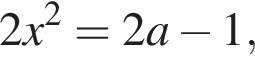 что также невозможно.
что также невозможно. Теперь первое уравнение системы принимает вид
Теперь первое уравнение системы принимает вид  В этом случае
В этом случае  откуда получаем единственное возможное значение
откуда получаем единственное возможное значение 

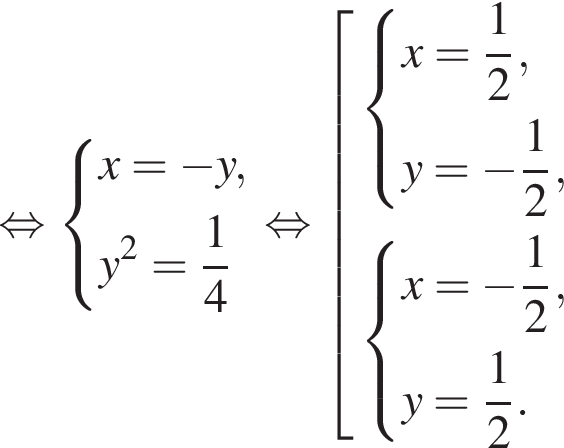




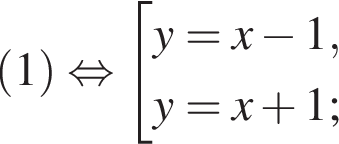

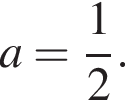 При этом значении параметра система принимает вид
При этом значении параметра система принимает вид 
 или
или  Такое значение параметра не подходит по условию. Следовательно, чтобы система имела ровно два решения, необходимо, чтобы
Такое значение параметра не подходит по условию. Следовательно, чтобы система имела ровно два решения, необходимо, чтобы 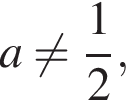 а потому
а потому 






 значит, этот случай не подходит. Найдем четверть дискриминанта:
значит, этот случай не подходит. Найдем четверть дискриминанта:  Полученное выражение обращается в нуль при
Полученное выражение обращается в нуль при 

 имеет решения?
имеет решения?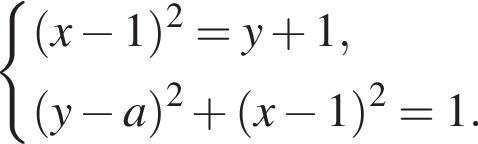



 Требование задачи будет выполнено, если последняя смешанная система имеет хотя бы одно решение. Искомые значения a находятся из совокупности неравенств
Требование задачи будет выполнено, если последняя смешанная система имеет хотя бы одно решение. Искомые значения a находятся из совокупности неравенств


 и
и 
 или
или  что дает
что дает 
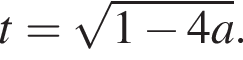 В этом случае
В этом случае  Тогда:
Тогда: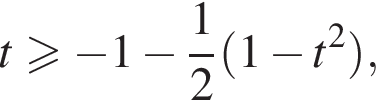 откуда
откуда 
 что дает
что дает 
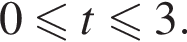 Возвращаясь к исходной переменной, получаем:
Возвращаясь к исходной переменной, получаем:






 имеет бесконечно много решений?
имеет бесконечно много решений? В общем случае две прямые, заданные уравнениями
В общем случае две прямые, заданные уравнениями  и
и 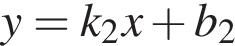 совпадают, если,
совпадают, если,  и
и  (при
(при  они имеют одну точку пересечения, при
они имеют одну точку пересечения, при  точек пересечения у них нет). Следовательно, система будет иметь бесконечно много решений в том случае, когда совместна система
точек пересечения у них нет). Следовательно, система будет иметь бесконечно много решений в том случае, когда совместна система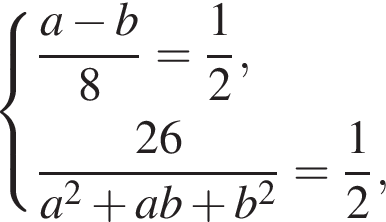
 или
или 






 имеет единственное решение при любом
имеет единственное решение при любом  Если
Если  или
или  и
и  соответственно. Исходная система будет иметь решения если существуют a и c, удовлетворяющие полученным соотношениям. При
соответственно. Исходная система будет иметь решения если существуют a и c, удовлетворяющие полученным соотношениям. При  и
и  Решая неравенства, находим
Решая неравенства, находим  и
и  Система должна иметь решения для любых значений b, поэтому найденные множества значений параметра а следует пересечь, получаем:
Система должна иметь решения для любых значений b, поэтому найденные множества значений параметра а следует пересечь, получаем: 
 и
и  После преобразований получим:
После преобразований получим:  и
и  Прямые не имеют общих точек тогда и только тогда, когда выполняются условия:
Прямые не имеют общих точек тогда и только тогда, когда выполняются условия:  и
и  Находим:
Находим:  и
и  Из первого уравнения находим
Из первого уравнения находим  Подставляя во второе соотношение, получим квадратные уравнения относительно с:
Подставляя во второе соотношение, получим квадратные уравнения относительно с:  и
и  Они не имеют корней, если а = 0 или если их дискриминанты отрицательны. Из условий
Они не имеют корней, если а = 0 или если их дискриминанты отрицательны. Из условий  и
и  получаем
получаем  При найденных значениях а система не имеет решений. При прочих — имеет.
При найденных значениях а система не имеет решений. При прочих — имеет.

 левая часть не имеет смысла. При
левая часть не имеет смысла. При  уравнение задаёт прямую
уравнение задаёт прямую  задаёт прямую с угловым коэффициентом a, проходящую через начало координат. Число решений исходной системы равно числу точек пересечения прямой
задаёт прямую с угловым коэффициентом a, проходящую через начало координат. Число решений исходной системы равно числу точек пересечения прямой 
 и при
и при  проходит через точку пересечения прямой
проходит через точку пересечения прямой  и при
и при 




 который удовлетворяет системе при
который удовлетворяет системе при  Второе уравнение имеет два различных корня
Второе уравнение имеет два различных корня  только при a > 0, причем x2 является корнем системы при любом положительном a, а x3 при
только при a > 0, причем x2 является корнем системы при любом положительном a, а x3 при  Таким образом, система будет иметь два различных решения при
Таким образом, система будет иметь два различных решения при  Кроме того, положительные корни x1 и x2 могут совпасть
Кроме того, положительные корни x1 и x2 могут совпасть  это происходит при a = 1.
это происходит при a = 1.
 множества значений a, возможно, с включением/исключением граничных точек
множества значений a, возможно, с включением/исключением граничных точек

 левая часть не имеет смысла. При
левая часть не имеет смысла. При  уравнение задаёт прямую
уравнение задаёт прямую  и
и  При этом прямая
При этом прямая 
 и при
и при 
 который удовлетворяет системе при
который удовлетворяет системе при  Второе уравнение имеет два различных корня
Второе уравнение имеет два различных корня  только при a > 0, причем, x2 является корнем системы при любом положительном a, а x3 при
только при a > 0, причем, x2 является корнем системы при любом положительном a, а x3 при  Таким образом, система будет иметь два различных решения при
Таким образом, система будет иметь два различных решения при  Кроме того, положительные корни x1 и x2 могут совпасть
Кроме того, положительные корни x1 и x2 могут совпасть  это происходит при a = 3.
это происходит при a = 3.
 множества значений a, возможно, с включением/исключением граничных точек
множества значений a, возможно, с включением/исключением граничных точек
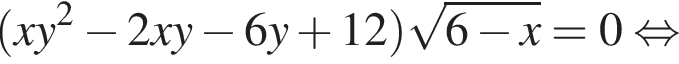




 два решения, при
два решения, при  три решения, при
три решения, при  четыре решения, при
четыре решения, при 




 имеют с прямой
имеют с прямой  две различных точки пересечения на области
две различных точки пересечения на области  (см. рис.).
(см. рис.). система имеет одно решение;
система имеет одно решение; — два решения;
— два решения;  — три решения;
— три решения;
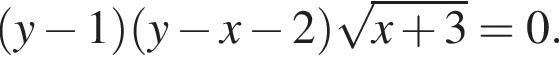 Решения первого уравнения системы совпадают с решениями уравнений
Решения первого уравнения системы совпадают с решениями уравнений 
 имеет единственное решение при любом значении a.
имеет единственное решение при любом значении a. откуда
откуда  C учётом условия
C учётом условия  получаем, что при
получаем, что при  решений нет, а при
решений нет, а при  имеется одно решение.
имеется одно решение. откуда
откуда  C учётом условия
C учётом условия  решений нет, а при
решений нет, а при  имеет одно решение.
имеет одно решение.
 либо
либо  откуда
откуда  либо
либо  откуда
откуда 
 имеет два решения при
имеет два решения при  и
и  и/или
и/или 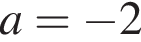
 множества значений a, возможно, с включением/исключением граничных точек
множества значений a, возможно, с включением/исключением граничных точек
 и
и  то получаем уравнение
то получаем уравнение



 Случаю удовлетворяют отрезки внутри квадрата
Случаю удовлетворяют отрезки внутри квадрата  то получаем уравнение
то получаем уравнение


 Случаю удовлетворяет только дуга ниже оси Ox.
Случаю удовлетворяет только дуга ниже оси Ox.  и
и 


 Случаю удовлетворяет только дуга левее оси Oy.
Случаю удовлетворяет только дуга левее оси Oy.  и
и 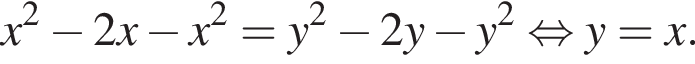


 являются точками пересечения полученных парабол с полученными прямыми и лежат на прямых
являются точками пересечения полученных парабол с полученными прямыми и лежат на прямых  дуги
дуги  с концами в точках B и C и дуги
с концами в точках B и C и дуги  с концами в точках A и C (см. рис.)
с концами в точках A и C (см. рис.)


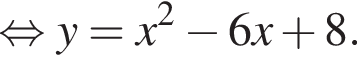



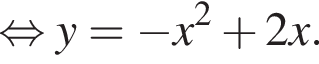

 c концом в точке
c концом в точке  во втором — прямую l, задаваемую уравнением х = 2, в третьем — дугу
во втором — прямую l, задаваемую уравнением х = 2, в третьем — дугу  с концом в точке А (см. рис.).
с концом в точке А (см. рис.). 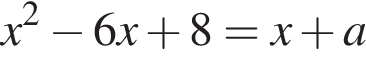 и
и  как квадратные относительно x и найдем, при каких значениях параметра их дискриминанты обращаются в нуль. Таким образом, при
как квадратные относительно x и найдем, при каких значениях параметра их дискриминанты обращаются в нуль. Таким образом, при  и
и  имеет две общие точки с дугой
имеет две общие точки с дугой  имеет одну общую точку с дугой
имеет одну общую точку с дугой  имеет две общие точки с дугой
имеет две общие точки с дугой 
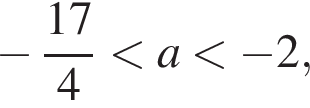

 или
или  ; возможно, с включением граничных точек
; возможно, с включением граничных точек
 уравнение
уравнение  принимает вид
принимает вид  при
при  его можно записать в виде
его можно записать в виде 
 Уравнение (**) задает окружность с центром в точке (1; 0) и радиусом
Уравнение (**) задает окружность с центром в точке (1; 0) и радиусом  получаемых сдвигом прямой
получаемых сдвигом прямой  лежат между прямыми m и n (см. рис.). Здесь прямая m проходит через точку (−1; 1), а прямая n является касательной к окружности.
лежат между прямыми m и n (см. рис.). Здесь прямая m проходит через точку (−1; 1), а прямая n является касательной к окружности. 






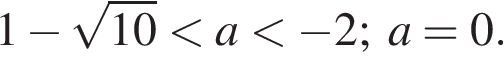


 которая имеет единственное решение
которая имеет единственное решение 



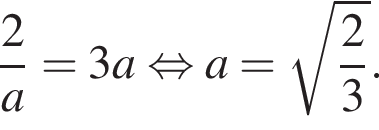 Заметим, что при любых положительных значениях a эти две прямые лежат ниже прямой
Заметим, что при любых положительных значениях a эти две прямые лежат ниже прямой  (на рисунке изображены синим цветом). Если две прямые совпадают, то у системы не может быть больше четырёх решений. Поэтому
(на рисунке изображены синим цветом). Если две прямые совпадают, то у системы не может быть больше четырёх решений. Поэтому 
 в двух различных точках в четвертой координатной четверти. Для этого нужно, чтобы гипербола дважды пересекала одну из прямых (на рисунке — красные точки), и не имела общих точек с другой прямой. (Ситуация, при которой каждая из прямых имеет одну общую точку с гиперболой и эти точки различны, невозможна.) Для этого нужно, чтобы из двух квадратных уравнений
в двух различных точках в четвертой координатной четверти. Для этого нужно, чтобы гипербола дважды пересекала одну из прямых (на рисунке — красные точки), и не имела общих точек с другой прямой. (Ситуация, при которой каждая из прямых имеет одну общую точку с гиперболой и эти точки различны, невозможна.) Для этого нужно, чтобы из двух квадратных уравнений и
и 




 приходим к ответу.
приходим к ответу.
 но неверно определены промежутки значений a
но неверно определены промежутки значений a  и
и  возможно, с включением граничных точек
возможно, с включением граничных точек
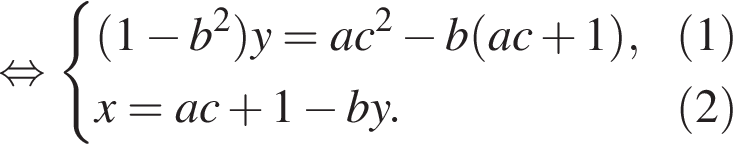

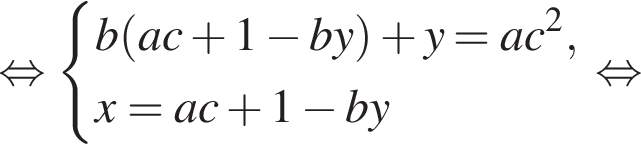
 и
и 



 Следовательно, не существует таких значений а, при которых хотя бы при одном c система уравнений имеет решения для любых значений b.
Следовательно, не существует таких значений а, при которых хотя бы при одном c система уравнений имеет решения для любых значений b.





 Тогда исходная система или имеет единственное решение
Тогда исходная система или имеет единственное решение  или не имеет решений.
или не имеет решений.


 (*)
(*) находим
находим  и
и 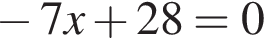 соответственно, имеющим единственное решение.
соответственно, имеющим единственное решение.
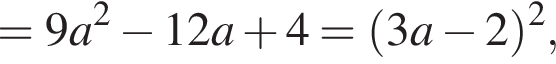



 На ОДЗ преобразуем второе уравнение системы:
На ОДЗ преобразуем второе уравнение системы: 





 прямая
прямая  изображенная на на рисунке зелёным цветом, проходит через выколотые точки гиперболы: точки
изображенная на на рисунке зелёным цветом, проходит через выколотые точки гиперболы: точки  где
где 
 этого уравнения равен нулю. Тогда
этого уравнения равен нулю. Тогда 


 система имеет два решения, а при
система имеет два решения, а при  или
или 


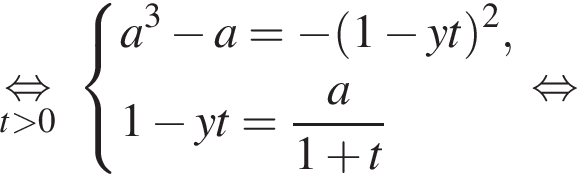



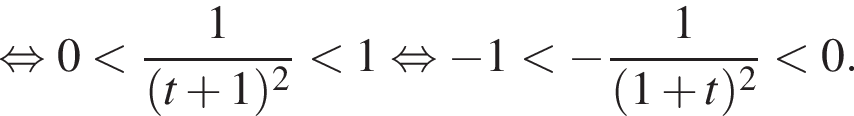


 Решим это двойное неравенство методом интервалов:
Решим это двойное неравенство методом интервалов:




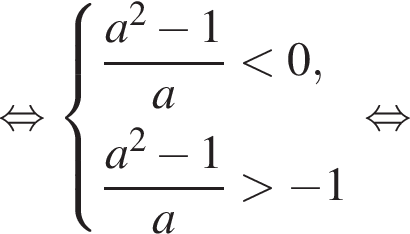








 количество решений системы совпадает с количеством решений уравнения
количество решений системы совпадает с количеством решений уравнения 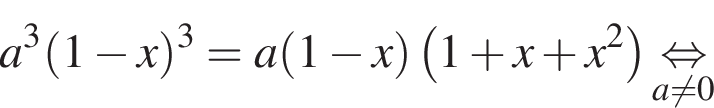

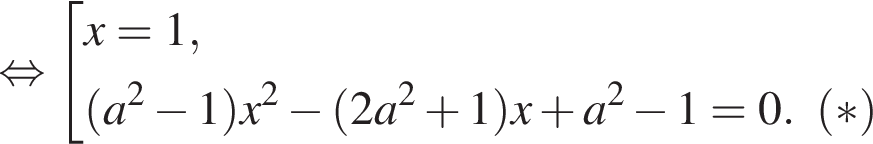
 уравнение (⁎) является линейным и имеет единственный корень
уравнение (⁎) является линейным и имеет единственный корень  уравнение (⁎) является квадратным и имеет не более одного корня, если его дискриминант неположителен. Имеем:
уравнение (⁎) является квадратным и имеет не более одного корня, если его дискриминант неположителен. Имеем:




 или если
или если 

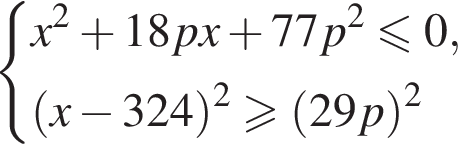



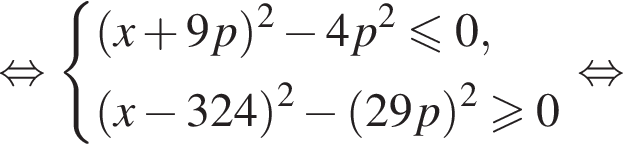
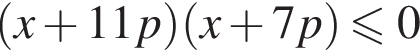 это вертикальные углы, образованные прямыми
это вертикальные углы, образованные прямыми  и
и  (см. рис., выделено синим);
(см. рис., выделено синим);  это вертикальные углы, образованные прямыми
это вертикальные углы, образованные прямыми  и
и  (выделено красным).
(выделено красным).  или
или  где
где 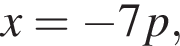 а
а 

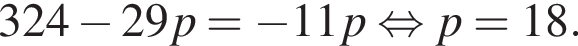
 или
или 

 или
или  система имеет бесконечно много решений, если
система имеет бесконечно много решений, если 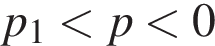 или
или 


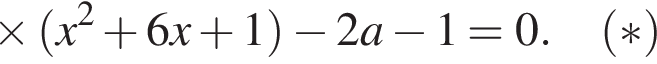



 Заметим, что
Заметим, что 




 Каждому значению
Каждому значению  соответствуют два значения переменной x, а значению
соответствуют два значения переменной x, а значению  — одно значение переменной x. Тогда уравнение (⁎) записывается в виде
— одно значение переменной x. Тогда уравнение (⁎) записывается в виде



 не имеет решений. Если
не имеет решений. Если 




 или при
или при 


 Заметим, что
Заметим, что 






 Графиком второго уравнения системы будет являться окружность (вырождающаяся в точку при
Графиком второго уравнения системы будет являться окружность (вырождающаяся в точку при 
 система (⁎) не имеет решений, а значит, и исходная система не имеет решений.
система (⁎) не имеет решений, а значит, и исходная система не имеет решений. система (⁎) имеет два решения (выделено красным), причём для обоих решений
система (⁎) имеет два решения (выделено красным), причём для обоих решений  система (⁎) имеет четыре решения (выделено зелёным), причём для всех решений
система (⁎) имеет четыре решения (выделено зелёным), причём для всех решений  система (⁎) имеет шесть решений (выделено оранжевым), для четырёх из которых
система (⁎) имеет шесть решений (выделено оранжевым), для четырёх из которых  система (⁎) имеет шесть решений, причём для всех решений
система (⁎) имеет шесть решений, причём для всех решений  система (⁎) имеет три решения (выделено небесно-голубым), причём для всех решений
система (⁎) имеет три решения (выделено небесно-голубым), причём для всех решений  система (⁎) не имеет решений, а значит и исходная система не имеет решений.
система (⁎) не имеет решений, а значит и исходная система не имеет решений.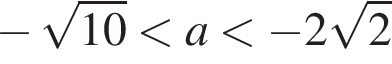 или
или 


 Заметим, что
Заметим, что 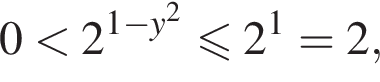
 Каждому значению
Каждому значению  соответствуют два значения переменной y, а значению
соответствуют два значения переменной y, а значению 



 при
при 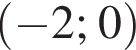 и радиусом
и радиусом  C учётом ограничения
C учётом ограничения  остаются две дуги и точка (выделено синим). Графиком второго уравнения системы (⁎) является прямая
остаются две дуги и точка (выделено синим). Графиком второго уравнения системы (⁎) является прямая  положение которой зависит от параметра a.
положение которой зависит от параметра a.  должна проходить через одну из точек
должна проходить через одну из точек 


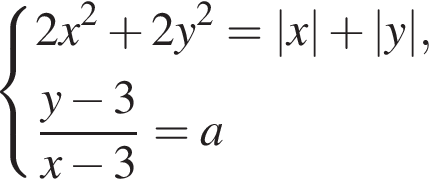



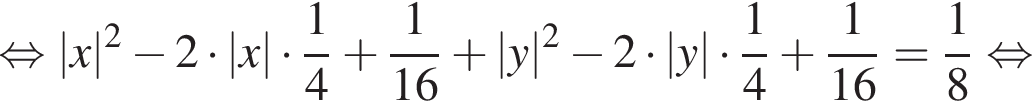



 то есть является уравнением окружности с центром в точке
то есть является уравнением окружности с центром в точке  и радиусом
и радиусом  Таким образом, при
Таким образом, при  является пучок прямых, проходящих через точку
является пучок прямых, проходящих через точку  Количество решений исходной системы совпадает с количеством точек пересечения графиков ее уравнений. Тем самым (см. рис.) исходная система может не иметь решений, либо иметь одно, два, три или четыре решения.
Количество решений исходной системы совпадает с количеством точек пересечения графиков ее уравнений. Тем самым (см. рис.) исходная система может не иметь решений, либо иметь одно, два, три или четыре решения.  если прямая
если прямая  если прямая
если прямая  или при
или при  если прямая проходит через точку
если прямая проходит через точку  (выделено зелёным),
(выделено зелёным),  если прямая
если прямая  Найдём
Найдём 



 которое равно радиусу
которое равно радиусу 







 и
и 




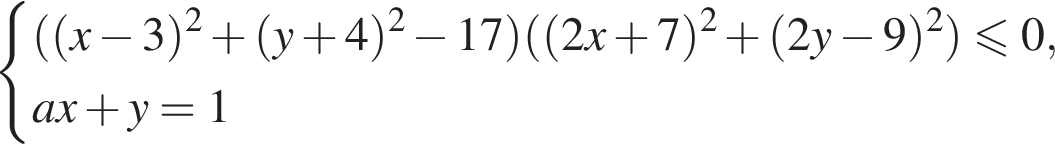
 и точки
и точки  Единственное решение будет тогда и только тогда, когда прямая
Единственное решение будет тогда и только тогда, когда прямая  касается круга, но не проходит через точку M, или проходит через точку M, но не имеет общих точек с кругом. Составим систему:
касается круга, но не проходит через точку M, или проходит через точку M, но не имеет общих точек с кругом. Составим систему: 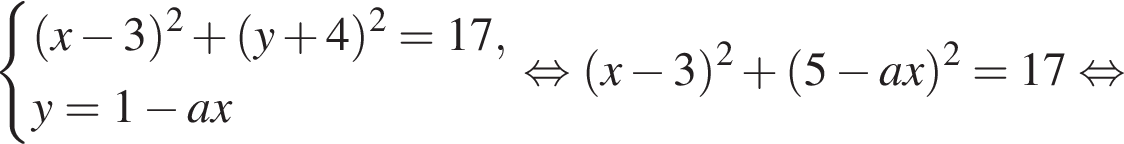







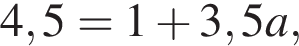 то есть
то есть 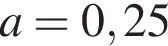 и
и  проходит через точку M. Проверим, пересекает ли она круг. Достаточно найти знак дискриминанта D при
проходит через точку M. Проверим, пересекает ли она круг. Достаточно найти знак дискриминанта D при 

 Второе уравнение задаёт две прямые
Второе уравнение задаёт две прямые  или
или  Центр ромба удалён от прямой
Центр ромба удалён от прямой  или
или  а центр ромба удалён от прямой
а центр ромба удалён от прямой 

 Следовательно, данная система не имеет решения тогда и только тогда, когда второму неравенству системы не удовлетворяет ни одно из решений первого неравенства.
Следовательно, данная система не имеет решения тогда и только тогда, когда второму неравенству системы не удовлетворяет ни одно из решений первого неравенства.
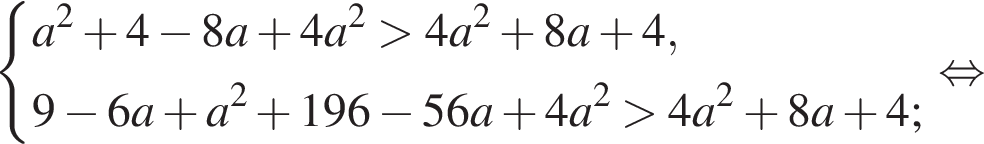


















 пересекает график первого уравнения системы в точке
пересекает график первого уравнения системы в точке  должна иметь с графиком первого уравнения системы не менее двух общих точек. Каждая из этих прямых проходит через точку с координатами
должна иметь с графиком первого уравнения системы не менее двух общих точек. Каждая из этих прямых проходит через точку с координатами 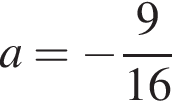 происходит касание прямой и гиперболы.
происходит касание прямой и гиперболы.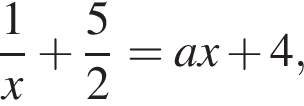 то есть уравнение
то есть уравнение  должно иметь единственное решение. Дискриминант полученного уравнения равен
должно иметь единственное решение. Дискриминант полученного уравнения равен  он обращается в нуль при
он обращается в нуль при 
 походит через точку B, а потому графики имеют лишь две общие точки.
походит через точку B, а потому графики имеют лишь две общие точки. отличных от
отличных от 






 и участка параболы
и участка параболы  на отрезке
на отрезке  с выколотыми точками
с выколотыми точками  Графиком второго уравнения для каждого значения параметра является горизонтальная прямая. Система имеет ровно два решения тогда и только тогда, когда графики уравнений имеют ровно две общие точки. Из построенных графиков находим искомые значения y:
Графиком второго уравнения для каждого значения параметра является горизонтальная прямая. Система имеет ровно два решения тогда и только тогда, когда графики уравнений имеют ровно две общие точки. Из построенных графиков находим искомые значения y:

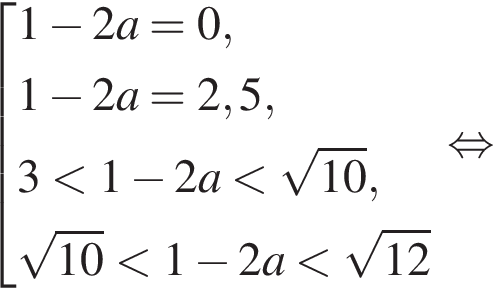



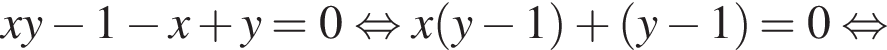





 и
и  и имеет два различных решения
и имеет два различных решения  входит в оба случая, а потому соответствующее значение параметра необходимо исключить. Найдем его, подставив решение
входит в оба случая, а потому соответствующее значение параметра необходимо исключить. Найдем его, подставив решение 
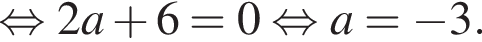
 в первое уравнение исходной системы и преобразуем полученное уравнение к квадратному относительно переменной y виду. Получим:
в первое уравнение исходной системы и преобразуем полученное уравнение к квадратному относительно переменной y виду. Получим:

 полученное уравнение решений не имеет, при прочих значениях параметра найдем дискриминант:
полученное уравнение решений не имеет, при прочих значениях параметра найдем дискриминант:


 или при
или при 












 или
или 










 лежащий не выше кривой
лежащий не выше кривой 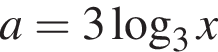 и не ниже кривой
и не ниже кривой  При
При  решением является отрезок
решением является отрезок 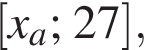 где
где  Значит, решением будет являться отрезок длиной 15, только если
Значит, решением будет являться отрезок длиной 15, только если  Это достигается при
Это достигается при 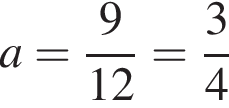 или при
или при 

 решается устно.
решается устно.
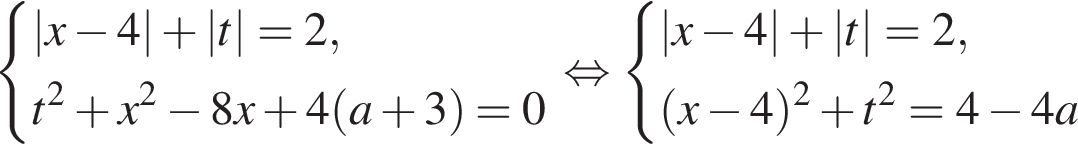


 второе уравнение, а значит, и вся система не имеет решений. При
второе уравнение, а значит, и вся система не имеет решений. При  решением второго уравнения является только пара чисел
решением второго уравнения является только пара чисел  в системе координат xOt графиком второго уравнения является окружность с центром в точке
в системе координат xOt графиком второго уравнения является окружность с центром в точке  а графиком первого уравнения являются стороны квадрата с вершинами в точках
а графиком первого уравнения являются стороны квадрата с вершинами в точках  Тогда ровно четыре решения система имеет в случаях, если окружность является либо вписанной в квадрат
Тогда ровно четыре решения система имеет в случаях, если окружность является либо вписанной в квадрат  либо описанной около квадрата
либо описанной около квадрата  в остальных случаях система либо не имеет решений, либо имеет восемь решений. Значит,
в остальных случаях система либо не имеет решений, либо имеет восемь решений. Значит,

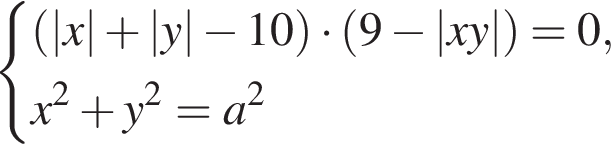






 а графиком второго уравнения является объединение двух гипербол (см. рис.). Точки пересечения гипербол и квадрата в первой четверти найдём из системы
а графиком второго уравнения является объединение двух гипербол (см. рис.). Точки пересечения гипербол и квадрата в первой четверти найдём из системы




 и
и 







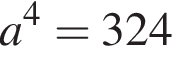 является число
является число  При этом значении параметра уравнение
При этом значении параметра уравнение  имеет ровно одно решение, лежащее в первой четверти, а потому в силу симметрии гипербола имеет с окружностью ровно 4 общих точки, лежащих по одной в каждой координатной четверти. При
имеет ровно одно решение, лежащее в первой четверти, а потому в силу симметрии гипербола имеет с окружностью ровно 4 общих точки, лежащих по одной в каждой координатной четверти. При  общих точек нет. При
общих точек нет. При 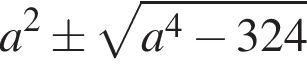 положительно, поэтому гипербола и окружность пересекаются в 8 точках, лежащих по две в каждой координатной четверти.
положительно, поэтому гипербола и окружность пересекаются в 8 точках, лежащих по две в каждой координатной четверти. 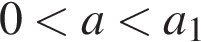 система не имеет решений;
система не имеет решений; система имеет 8 решений;
система имеет 8 решений; система имеет 16 решений;
система имеет 16 решений; система имеет 16 решений;
система имеет 16 решений;
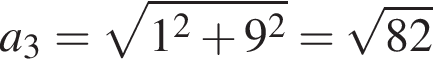
 (квадрат вписан в окружность).
(квадрат вписан в окружность). или
или 



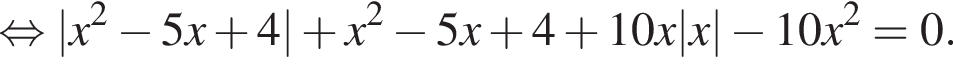





 и уравнение принимает вид
и уравнение принимает вид







 и
и 


 не выше прямой
не выше прямой 
 Абсциссы концов нижнего отрезка найдем из уравнения
Абсциссы концов нижнего отрезка найдем из уравнения  получим
получим  Разность абсцисс концов отрезков должна быть равна двум, имеем:
Разность абсцисс концов отрезков должна быть равна двум, имеем:



 или
или 

 Графиком второго уравнения системы является пучок прямых проходящих через точку
Графиком второго уравнения системы является пучок прямых проходящих через точку 
 система не имеет решений, при
система не имеет решений, при  система имеет одно решение, при
система имеет одно решение, при 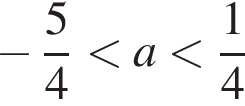 система имеет два решения,
система имеет два решения, 
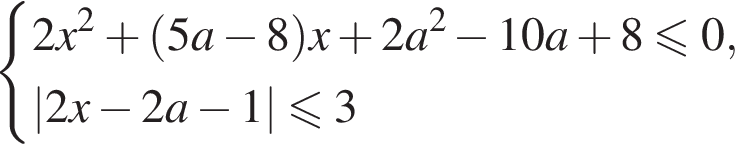



 и
и  включая сами прямые (выделено синим). Второму неравенству соответствует полоса между прямыми
включая сами прямые (выделено синим). Второму неравенству соответствует полоса между прямыми  и
и  включая сами прямые (выделено красным). Решением системы будут общие точки частей плоскости, соответствующих первому и второму неравенствам (выделено фиолетовым). Таким образом, система имеет хотя бы одно решение при
включая сами прямые (выделено красным). Решением системы будут общие точки частей плоскости, соответствующих первому и второму неравенствам (выделено фиолетовым). Таким образом, система имеет хотя бы одно решение при 



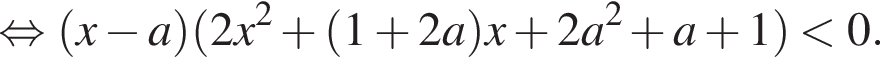
 равен
равен

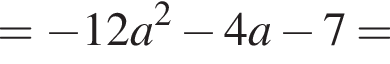


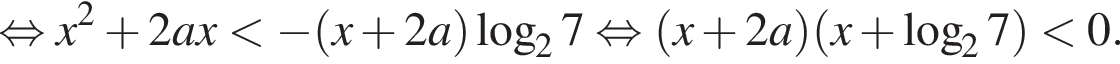


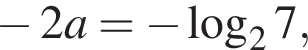 то неравенство
то неравенство 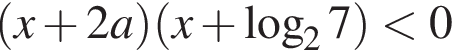 не имеет решений.
не имеет решений. то
то  и на отрезке [−2; 1] решений нет.
и на отрезке [−2; 1] решений нет. то получаем систему неравенств:
то получаем систему неравенств:  Чтобы на отрезке [−2; 1] было решение, нужно, чтобы наименьшее из чисел a и −2a было больше чем −2:
Чтобы на отрезке [−2; 1] было решение, нужно, чтобы наименьшее из чисел a и −2a было больше чем −2: 

 и
и  Первый график — парабола
Первый график — парабола  и второй — прямая
и второй — прямая  разбивают полуплоскость на 4 части, в двух из которых (выделены зелёным) неравенство выполняется.
разбивают полуплоскость на 4 части, в двух из которых (выделены зелёным) неравенство выполняется.  является пучок прямых
является пучок прямых  проходящих через точку с координатами
проходящих через точку с координатами 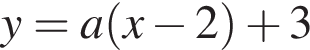 имеет только одну общую точку с выделенными зелёным частями плоскости. Это достигается в двух случаях.
имеет только одну общую точку с выделенными зелёным частями плоскости. Это достигается в двух случаях.  (выделено оранжевым). Тогда
(выделено оранжевым). Тогда 
 должно иметь единственное решение. Запишем его в виде
должно иметь единственное решение. Запишем его в виде  и найдем дискриминант:
и найдем дискриминант:


 При
При  абсцисса точки касания положительна, что не соответствует условию задачи. При
абсцисса точки касания положительна, что не соответствует условию задачи. При 
 имеет бесконечное число решений;
имеет бесконечное число решений; имеет одно решение;
имеет одно решение;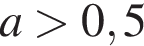 имеет бесконечное число решений.
имеет бесконечное число решений.


 пересекает левую ветвь гиперболы при
пересекает левую ветвь гиперболы при  и при
и при 







 три решения, при
три решения, при  два решения, при
два решения, при 

 задает окружность с центром в точке
задает окружность с центром в точке  и радиусом
и радиусом 






 касательными к окружности при найденных значениях параметра.
касательными к окружности при найденных значениях параметра. центр окружности имеет координаты
центр окружности имеет координаты  а радиус равен
а радиус равен  Расстояние от точки
Расстояние от точки  до прямых
до прямых  является верным, значит, при
является верным, значит, при  а радиус равен
а радиус равен  Расстояние от точки
Расстояние от точки  является неверным, значит, при
является неверным, значит, при 

 (выделено синим). При
(выделено синим). При  графиком второго уравнения является окружность с центром в точке
графиком второго уравнения является окружность с центром в точке  вырождающаяся в точку при
вырождающаяся в точку при  При
При  второе уравнение, а вместе с ним и вся система, решений не имеют.
второе уравнение, а вместе с ним и вся система, решений не имеют.  Значит, чтобы система имела нечётное число решений, окружность должна проходить либо через точку
Значит, чтобы система имела нечётное число решений, окружность должна проходить либо через точку  либо через точку
либо через точку 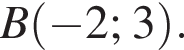 Найдём соответствующие значения параметра a.
Найдём соответствующие значения параметра a. при
при


 при
при


 радиус окружности равен 2 (выделено красным). Значит, окружность не имеет общих точек с прямой
радиус окружности равен 2 (выделено красным). Значит, окружность не имеет общих точек с прямой  центр окружности находится в точке
центр окружности находится в точке  радиус окружности равен 106 (выделено цветом фуксии). Значит, окружность не имеет общих точек с прямой
радиус окружности равен 106 (выделено цветом фуксии). Значит, окружность не имеет общих точек с прямой  радиус окружности равен 6 (выделено оранжевым). Тогда окружность касается прямой
радиус окружности равен 6 (выделено оранжевым). Тогда окружность касается прямой  значит, система имеет ровно пять решений.
значит, система имеет ровно пять решений. радиус окружности равен 18 (выделено зелёным). Тогда окружность касается прямой
радиус окружности равен 18 (выделено зелёным). Тогда окружность касается прямой 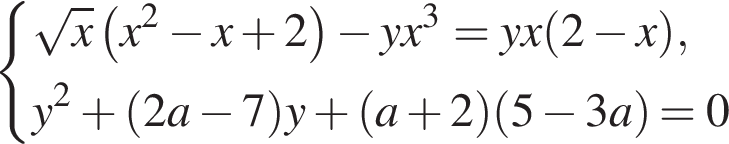
 Выражение
Выражение 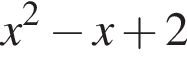 положительно при всех значениях x, поэтому на него можно разделить, откуда получаем уравнение
положительно при всех значениях x, поэтому на него можно разделить, откуда получаем уравнение 
 их сумма равна
их сумма равна  поэтому корни суть
поэтому корни суть  Получаем равносильную систему:
Получаем равносильную систему:
 и
и  если выполняется условие
если выполняется условие
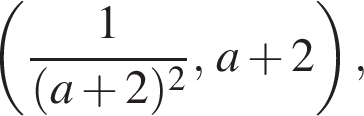 если выполняется условие
если выполняется условие
 Этими решениями являются пары чисел
Этими решениями являются пары чисел  и
и  При других значениях параметра исходная система будет иметь или три, или четыре различных решения.
При других значениях параметра исходная система будет иметь или три, или четыре различных решения.
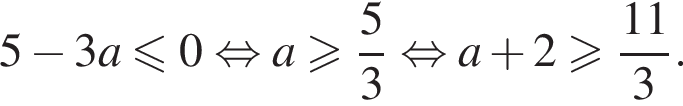
 система имеет три решения
система имеет три решения 

 система имеет четыре решения
система имеет четыре решения 



 система имеет четыре решения
система имеет четыре решения 





 и
и  Графиком неравенства системы является круг с центром в точке
Графиком неравенства системы является круг с центром в точке  и радиусом
и радиусом  при
при  вырождающийся в точку
вырождающийся в точку 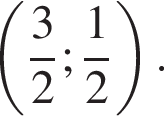 Прямые
Прямые  не проходят через точку
не проходят через точку 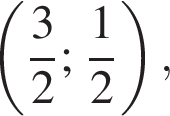 значит, система может иметь ровно одно решение только в случае, если одна из прямых является касательной к окружности
значит, система может иметь ровно одно решение только в случае, если одна из прямых является касательной к окружности 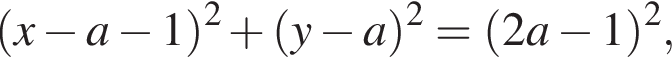
 Прямые
Прямые 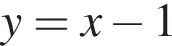 и
и  Прямые
Прямые  перпендикулярны и пересекаются в точке (0; −1), а потому прямая
перпендикулярны и пересекаются в точке (0; −1), а потому прямая  касается окружности в точке (0; −1).
касается окружности в точке (0; −1).

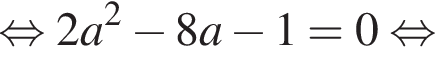

 окружность не имеет общих точек с прямой
окружность не имеет общих точек с прямой  а при
а при  или
или  прямая
прямая 
 прямая
прямая  прямая
прямая 



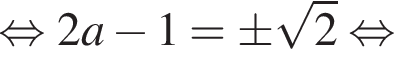
 значит, при
значит, при 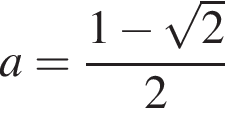 прямая
прямая  прямая
прямая 



 задает прямую
задает прямую  Система
Система 
 расположенную не выше прямой
расположенную не выше прямой  и параболы
и параболы  найдем из уравнения
найдем из уравнения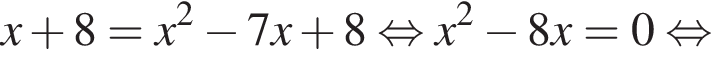


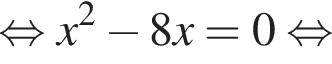
 задает семейство прямых, проходящих через точку (−1; 0). Если a = 1, то прямая
задает семейство прямых, проходящих через точку (−1; 0). Если a = 1, то прямая  В этом случае должно иметь единственное решение уравнение
В этом случае должно иметь единственное решение уравнение 



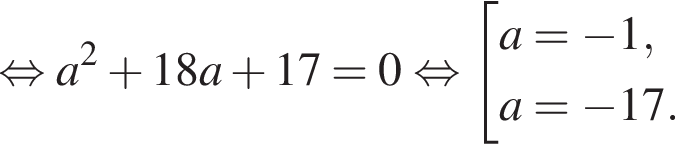




 При a = −1 находим: x = 3, соответствующая прямая изображена красным цветом. При a = −17 абсцисса точка касания x = −5 < 0, то есть точка касания не лежит на графике Г1.
При a = −1 находим: x = 3, соответствующая прямая изображена красным цветом. При a = −17 абсцисса точка касания x = −5 < 0, то есть точка касания не лежит на графике Г1. вторая лежит в четвертой четверти и является точкой касания с параболой.
вторая лежит в четвертой четверти и является точкой касания с параболой.  графики имеют три точки пересечений, две из которых лежат на параболе, а третья лежит на прямой
графики имеют три точки пересечений, две из которых лежат на параболе, а третья лежит на прямой  (случай
(случай  изображен зеленым) графики Г1 и Г2 пересекаются ровно в двух точках, одна из которых лежит на параболе, а вторая лежит на прямой
изображен зеленым) графики Г1 и Г2 пересекаются ровно в двух точках, одна из которых лежит на параболе, а вторая лежит на прямой 

 и гиперболы
и гиперболы  Графиком второго уравнения является прямая, параллельная прямой
Графиком второго уравнения является прямая, параллельная прямой  и проходящая через точку
и проходящая через точку  пересекаются при любом a, поэтому ровно два решения система будет иметь в случае, когда прямая
пересекаются при любом a, поэтому ровно два решения система будет иметь в случае, когда прямая  касается гиперболы или проходит через одну из точек пересечения гиперболы и прямой
касается гиперболы или проходит через одну из точек пересечения гиперболы и прямой 


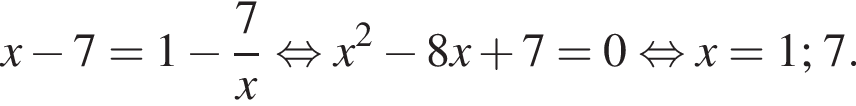


 и
и  соответственно.
соответственно.



 и дуги окружности радиуса 3 с центром в точке (−3; 0), лежащей выше этой прямой.
и дуги окружности радиуса 3 с центром в точке (−3; 0), лежащей выше этой прямой. и
и  пересекаются при любом a, поэтому система имеет два решения тогда и только тогда, когда прямая
пересекаются при любом a, поэтому система имеет два решения тогда и только тогда, когда прямая  касается дуги тогда, когда уравнение
касается дуги тогда, когда уравнение


 Получаем:
Получаем: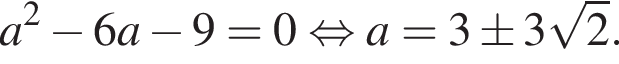
 прямая
прямая  а также пересекает один раз дугу, следовательно, исходная система имеет ровно два различных решения.
а также пересекает один раз дугу, следовательно, исходная система имеет ровно два различных решения.


 расположенную не выше прямой
расположенную не выше прямой  Найдем абсциссу вершины параболы:
Найдем абсциссу вершины параболы:  тогда
тогда 
 и
и 


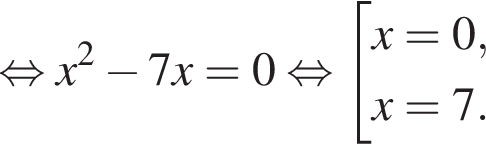
 имеет всегда одну общую точку с прямой
имеет всегда одну общую точку с прямой  так как не параллельна ей, следовательно, система будет иметь два различных решения в двух случаях:
так как не параллельна ей, следовательно, система будет иметь два различных решения в двух случаях: 
 ).
). имеет одно решение. Выполним преобразования:
имеет одно решение. Выполним преобразования:

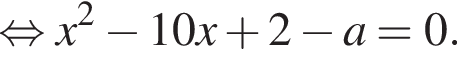

 имеет единственное решение, x = 5. Проверим, что при x = 5 точка касания лежит не ниже прямой
имеет единственное решение, x = 5. Проверим, что при x = 5 точка касания лежит не ниже прямой 


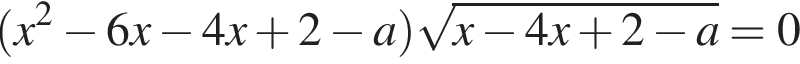 имеет 2 различных решения. Имеем:
имеет 2 различных решения. Имеем:
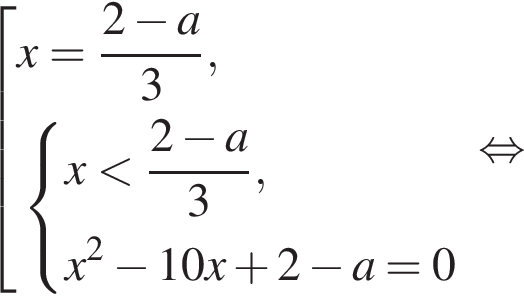


 — верно.
— верно.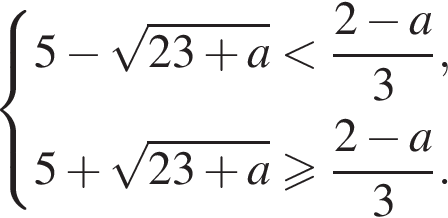
 тогда
тогда  Имеем:
Имеем:



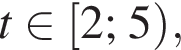 получаем:
получаем: 






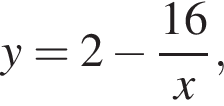 расположенную не ниже прямой
расположенную не ниже прямой 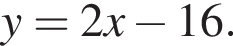 Найдем точки пересечения прямой
Найдем точки пересечения прямой  и гиперболы
и гиперболы 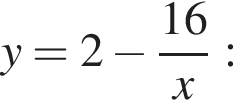




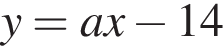 — это невертикальная прямая, проходящая через точку (0; −14). Если a < 0, то
— это невертикальная прямая, проходящая через точку (0; −14). Если a < 0, то 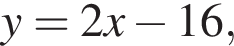 так как коэффициенты различны. Чтобы узнать, пересекает ли прямая
так как коэффициенты различны. Чтобы узнать, пересекает ли прямая  гиперболу
гиперболу  решим уравнение
решим уравнение 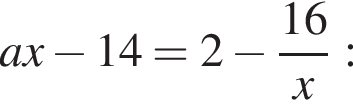

 и
и  но поскольку a < 0, то
но поскольку a < 0, то  следовательно, с правой частью гиперболы
следовательно, с правой частью гиперболы  прямая
прямая  — эта прямая параллельна оси x, следовательно, имеет с гиперболой
— эта прямая параллельна оси x, следовательно, имеет с гиперболой 


 Если с гиперболой нет общих точек, то решений не более 1 и такая ситуация не подходит.
Если с гиперболой нет общих точек, то решений не более 1 и такая ситуация не подходит. 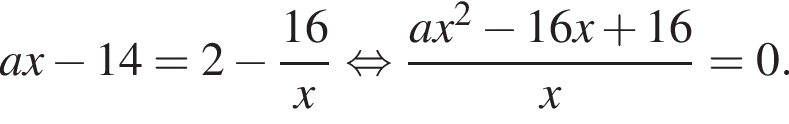
 равен нулю:
равен нулю: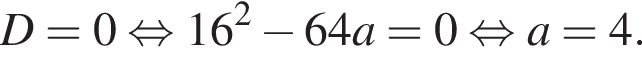





 (при a > 0). Если
(при a > 0). Если  то
то 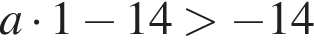 —
— 
 — два различных решения.
— два различных решения.
 имеет два различных решения. Выполним преобразования:
имеет два различных решения. Выполним преобразования:






 Его дискриминант равен
Его дискриминант равен  Если D > 0, то
Если D > 0, то 
 — всего 2 решения, a = 4 подходит. Если D < 0, то всего 1 решение, что не подходит.
— всего 2 решения, a = 4 подходит. Если D < 0, то всего 1 решение, что не подходит.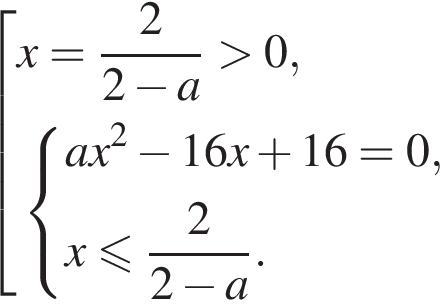

 и должно выполняться
и должно выполняться  чтобы было 2 решения. Имеем:
чтобы было 2 решения. Имеем:










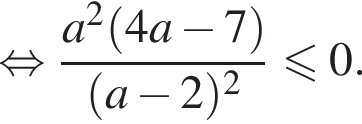


 должен быть больше или равен
должен быть больше или равен  должен быть меньше
должен быть меньше 






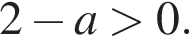 Если
Если  то (1) верно, а (2) преобразится в
то (1) верно, а (2) преобразится в 


 то получим, что
то получим, что  Если
Если  то (1) и (2) верно —
то (1) и (2) верно —  то (2) верно, а (1) преобразуется в
то (2) верно, а (1) преобразуется в 
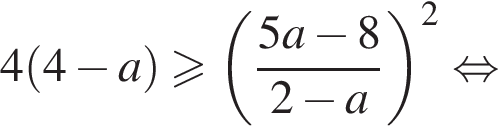

 то
то 


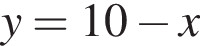 и части графика
и части графика  лежащей ниже этой прямой (выделено оранжевым). При
лежащей ниже этой прямой (выделено оранжевым). При  это отрезок AD прямой
это отрезок AD прямой  где
где  — точка прямой с абсциссой
— точка прямой с абсциссой  — точка её пересечения с
— точка её пересечения с 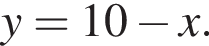 При
При  функция имеет вид
функция имеет вид  — точка прямой с абсциссой
— точка прямой с абсциссой  где
где  — точка её пересечения с
— точка её пересечения с  Откуда и следует ответ.
Откуда и следует ответ.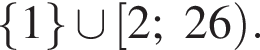
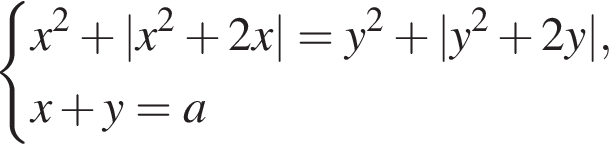
 и
и  то получаем уравнение
то получаем уравнение то получаем уравнение
то получаем уравнение


 Случаю удовлетворяет только дуга, лежащая выше оси Ox и расположенная между прямыми
Случаю удовлетворяет только дуга, лежащая выше оси Ox и расположенная между прямыми  и
и 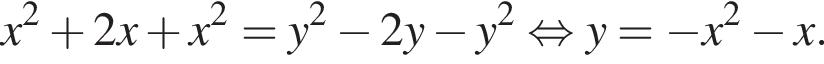


 Случаю удовлетворяет только дуга, лежащая правее оси Oy и заключенная между прямыми
Случаю удовлетворяет только дуга, лежащая правее оси Oy и заключенная между прямыми 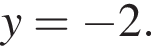
 и
и 



 и
и 
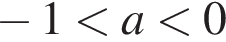 прямая m пересекает график Г в трех точках точках, а значит, исходная система имеет три решения.
прямая m пересекает график Г в трех точках точках, а значит, исходная система имеет три решения.

 и
и  то получаем уравнение:
то получаем уравнение: 



 то получаем уравнение:
то получаем уравнение: 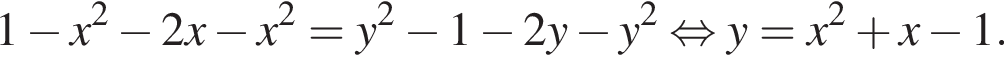


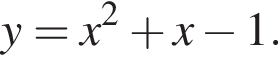
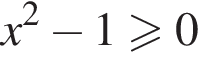 и
и 



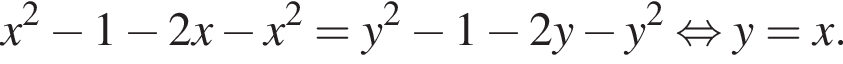


 и/или
и/или  поэтому искомое множество состоит из прямой l, задаваемой уравнением
поэтому искомое множество состоит из прямой l, задаваемой уравнением  дуги
дуги  с концами в точках B и C и дуги
с концами в точках B и C и дуги  с концами в точках A и C (см. рис.).
с концами в точках A и C (см. рис.).  прямая m содержит отрезок AB, то есть исходная система имеет бесконечное число решений.
прямая m содержит отрезок AB, то есть исходная система имеет бесконечное число решений.  прямая m касается дуг
прямая m касается дуг  прямая m не пересекает отрезок AB, пересекает прямую l в точке, отличной от точки C, и пересекает каждую из дуг
прямая m не пересекает отрезок AB, пересекает прямую l в точке, отличной от точки C, и пересекает каждую из дуг  прямая m пересекает прямую l в одной точке и не пересекает дуги
прямая m пересекает прямую l в одной точке и не пересекает дуги 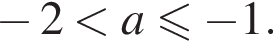
 отвечает этому требованию для обеих парабол.
отвечает этому требованию для обеих парабол.




 Количество решений исходной системы равно количеству точек пересечения построенных графиков. Поэтому исходная система:
Количество решений исходной системы равно количеству точек пересечения построенных графиков. Поэтому исходная система:  имеет одно решение;
имеет одно решение; три решения;
три решения; три решения;
три решения; два решения;
два решения;


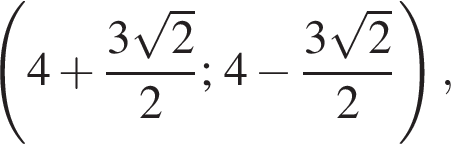 тогда
тогда



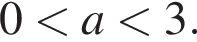

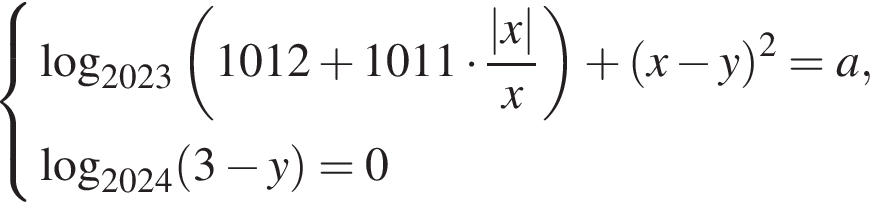





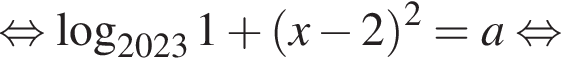

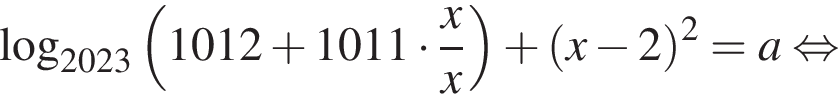



 имеет два положительных корня, при
имеет два положительных корня, при 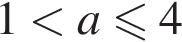 и
и 



 и
и  получим равносильную систему с таким же количеством решений, так как u и υ суть линейные выражения. Тогда:
получим равносильную систему с таким же количеством решений, так как u и υ суть линейные выражения. Тогда:
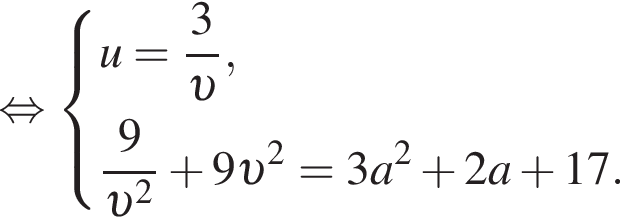
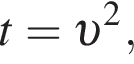
 Чтобы найти, при каких значениях параметра исходная система имеет ровно два различных решения, нужно найти, при каких a последнее уравнение имеет единственное решение.
Чтобы найти, при каких значениях параметра исходная система имеет ровно два различных решения, нужно найти, при каких a последнее уравнение имеет единственное решение.  известен, наименьшее значений этой функции при
известен, наименьшее значений этой функции при  получается из него растяжением в 9 раз вдоль оси ординат (см. рис.). Поэтому
получается из него растяжением в 9 раз вдоль оси ординат (см. рис.). Поэтому 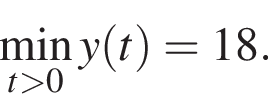 Прямая
Прямая  имеет единственное пересечение с этим графиком при
имеет единственное пересечение с этим графиком при  Таким образом,
Таким образом,







 его графиком являются две параболы, симметричные относительно оси абсцисс, с общими точками (0; 0) и (2; 0).
его графиком являются две параболы, симметричные относительно оси абсцисс, с общими точками (0; 0) и (2; 0).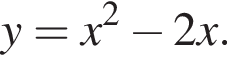 Решим соответствующее уравнение и найдём нуль дискриминанта:
Решим соответствующее уравнение и найдём нуль дискриминанта:
 он равен нулю при
он равен нулю при  откуда
откуда 
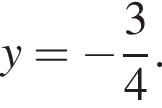
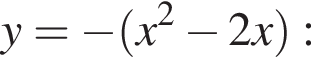

 он равен нулю при
он равен нулю при  откуда
откуда 

 то у прямой y = a – x нет общих точек с графиком
то у прямой y = a – x нет общих точек с графиком  а с графиком
а с графиком  — две общие точки.
— две общие точки.  то у прямой y = a – x одна общая точка
то у прямой y = a – x одна общая точка  с графиком
с графиком  значит, будет 3 общих точки.
значит, будет 3 общих точки. то прямая y = a – x пересекает каждую параболу в двух точках, которые не могут совпасть полностью, так как это происходит в точках (0; 0) и (2; 0), поэтому будет минимум 3 решения.
то прямая y = a – x пересекает каждую параболу в двух точках, которые не могут совпасть полностью, так как это происходит в точках (0; 0) и (2; 0), поэтому будет минимум 3 решения. то у прямой y = a – x одна общая точка
то у прямой y = a – x одна общая точка  с графиком
с графиком  то у прямой y = a – x нет общих точек с графиком
то у прямой y = a – x нет общих точек с графиком 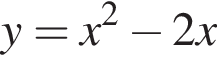 — две общие точки.
— две общие точки. 

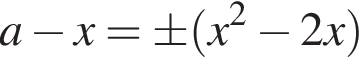 имело равно два различных решения.
имело равно два различных решения.
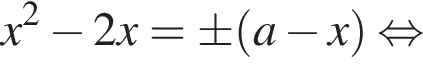

 дискриминант уравнения (2) равен
дискриминант уравнения (2) равен  его корни
его корни 


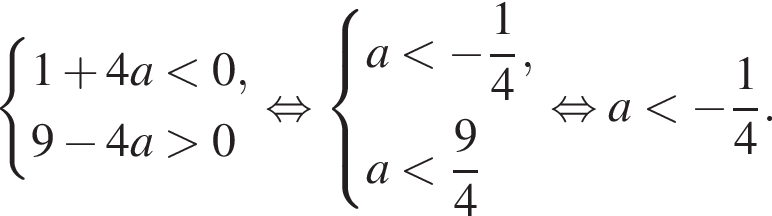

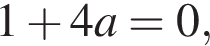 значит,
значит,  Необходимо, чтобы
Необходимо, чтобы 

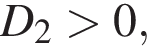 x1 = x3, x2 = x4:
x1 = x3, x2 = x4: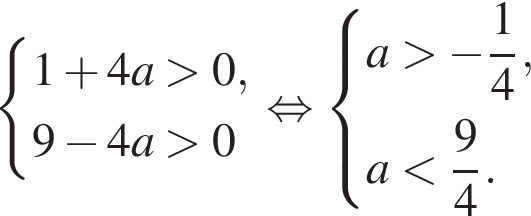


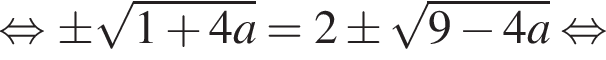










 — не подходит.
— не подходит.




 значит,
значит, 
 — не подходит.
— не подходит.
 — не подходит.
— не подходит.

 что противоречит второму уравнению системы. При
что противоречит второму уравнению системы. При 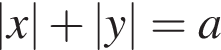 задает на координатной плоскости квадрат с вершинами на координатных осях и диагоналями, равными 2a. График второго уравнения получается из графика функции
задает на координатной плоскости квадрат с вершинами на координатных осях и диагоналями, равными 2a. График второго уравнения получается из графика функции  сдвигом на четыре единицы влево вдоль оси абсцисс.
сдвигом на четыре единицы влево вдоль оси абсцисс. имеет единственное решение. Имеем:
имеет единственное решение. Имеем:



 имеет единственное решение в том случае, если дискриминант равен нулю. Решим уравнение
имеет единственное решение в том случае, если дискриминант равен нулю. Решим уравнение 


 имеет единственное решение в том случае, если дискриминант равен нулю. Решим уравнение
имеет единственное решение в том случае, если дискриминант равен нулю. Решим уравнение 


 и
и  касаются при
касаются при  При найденном значении а абсциссой точки касания является
При найденном значении а абсциссой точки касания является  эта точка действительно лежит на стороне квадрата. Следовательно, система уравнений имеет два решения при
эта точка действительно лежит на стороне квадрата. Следовательно, система уравнений имеет два решения при  и
и 


 представляет собой график функции
представляет собой график функции  сдвинутый на
сдвинутый на 
 является касательной к параболе
является касательной к параболе 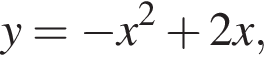 а прямая
а прямая  — касательной к параболе
— касательной к параболе 




 Второе — часть гиперболы
Второе — часть гиперболы  при
при  если
если  Ясно, что при
Ясно, что при  тогда
тогда
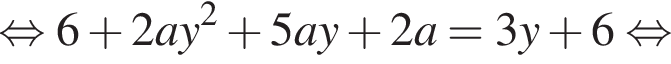



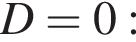



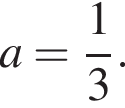 Теперь из геометрических соображений получаем, что при
Теперь из геометрических соображений получаем, что при  решений системы не меньше двух. Если же
решений системы не меньше двух. Если же  то решение ровно одно. В итоге получаем ответ:
то решение ровно одно. В итоге получаем ответ: 



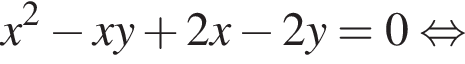
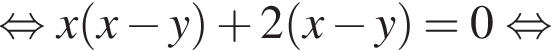

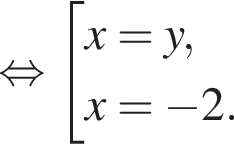
 то
то




 и
и 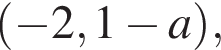 которые совпадают при
которые совпадают при 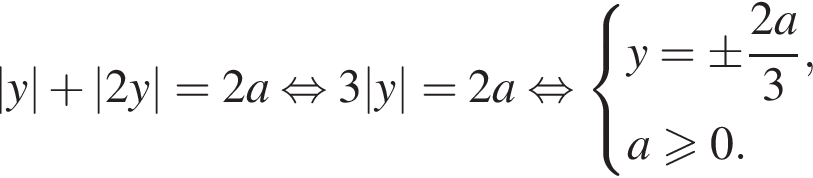


 и
и  которые совпадают при
которые совпадают при  то есть должно выполняться условие
то есть должно выполняться условие 
 множества значений a, возможно, с включением граничной точки
множества значений a, возможно, с включением граничной точки



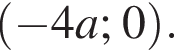 Графиком второго уравнения системы является окружность с центром в точке
Графиком второго уравнения системы является окружность с центром в точке 

 равно 5:
равно 5:






 или
или 


 являются решением исходной системы, то система имеет бесконечное число решений. Значит, чтобы система имела ровно четыре различных решения, решения уравнения
являются решением исходной системы, то система имеет бесконечное число решений. Значит, чтобы система имела ровно четыре различных решения, решения уравнения 


 а условию
а условию  соответствуют все точки лежащие выше параболы
соответствуют все точки лежащие выше параболы  Таким образом, система будет иметь конечное число решений в двух случаях:
Таким образом, система будет иметь конечное число решений в двух случаях:  принадлежит левой ветви параболы (выделено синим) или лежит левее, что выполняется при
принадлежит левой ветви параболы (выделено синим) или лежит левее, что выполняется при 
 принадлежит правой ветви параболы (выделено оранжевым) или лежит правее, что выполняется при
принадлежит правой ветви параболы (выделено оранжевым) или лежит правее, что выполняется при 





 радиусом 1 и параболы
радиусом 1 и параболы  (выделены синим).
(выделены синим). Преобразуем второе уравнение полученной системы:
Преобразуем второе уравнение полученной системы:

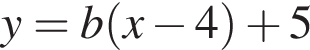 дважды пересекает окружность
дважды пересекает окружность 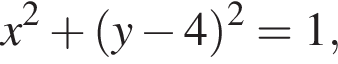 то есть когда расстояние от центра окружности до прямой меньше радиуса окружности:
то есть когда расстояние от центра окружности до прямой меньше радиуса окружности:







 получаем:
получаем:
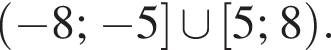





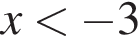 решений нет. Рассмотрим случай
решений нет. Рассмотрим случай 


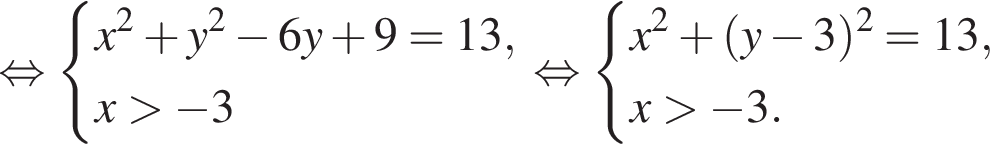

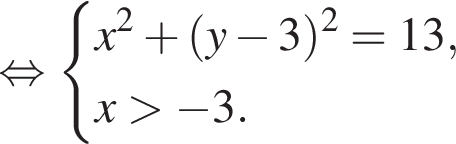




 проходит через точку A при
проходит через точку A при  которая перпендикулярна прямой
которая перпендикулярна прямой 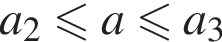 два решения;
два решения;


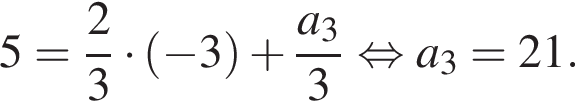


 и
и 





 преобразуем первое уравнение системы. Воспользуемся формулой косинуса тройного аргумента
преобразуем первое уравнение системы. Воспользуемся формулой косинуса тройного аргумента 

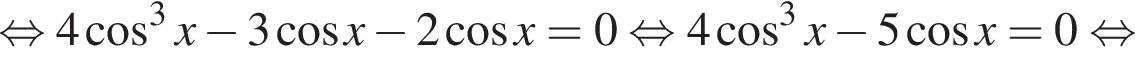
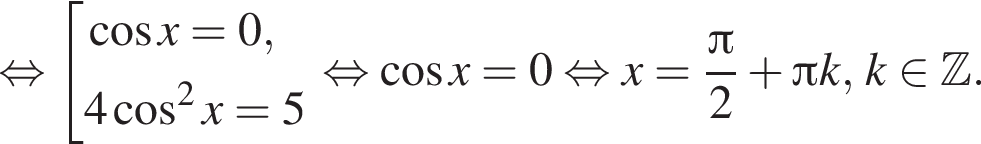

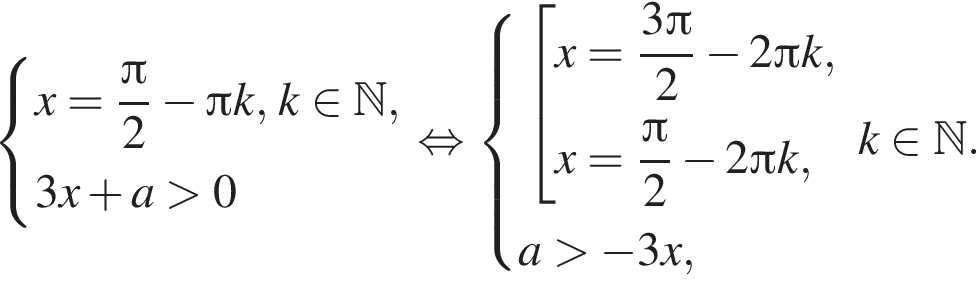
 является решением системы, а число
является решением системы, а число  — не является. Тогда при
— не является. Тогда при  где
где 
 а тогда
а тогда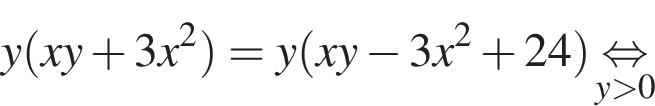

 откуда находим:
откуда находим:


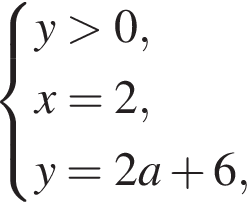
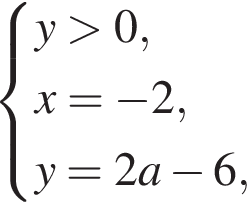

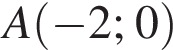 и
и  Если прямая
Если прямая  проходит через точку A, исходная система имеет два различных решения; в этом случае
проходит через точку A, исходная система имеет два различных решения; в этом случае  то есть
то есть  то есть
то есть  Определим значение параметра, при котором прямая
Определим значение параметра, при котором прямая  Касательная имеет с гиперболой единственную общую точку, а потому уравнение
Касательная имеет с гиперболой единственную общую точку, а потому уравнение  имеет единственное решение. Умножим обе части на х, сведем уравнение к квадратному, получим:
имеет единственное решение. Умножим обе части на х, сведем уравнение к квадратному, получим:  Найдем четверть дискриминанта:
Найдем четверть дискриминанта:  Дискриминант обращается в нуль при
Дискриминант обращается в нуль при  Найденным значениям параметра соответствуют точки касания
Найденным значениям параметра соответствуют точки касания  Отрицательной ординате точки касания соответствует значение
Отрицательной ординате точки касания соответствует значение 


 и при
и при 


 Тогда система неравенств примет вид:
Тогда система неравенств примет вид:



 тогда исходная система примет вид:
тогда исходная система примет вид:

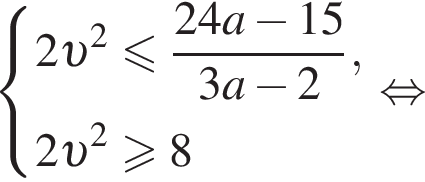

 Значит, при всех
Значит, при всех 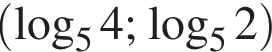 будет являться решением исходной системы, то есть система будет иметь хотя бы одно решение.
будет являться решением исходной системы, то есть система будет иметь хотя бы одно решение.

 прямой
прямой  можно записать в виде
можно записать в виде  оно задаёт пучок прямых, проходящих через точку
оно задаёт пучок прямых, проходящих через точку  При
При  (выделено синим) прямая проходит через точку
(выделено синим) прямая проходит через точку  принадлежит выделенным областям.
принадлежит выделенным областям. система имеет бесконечное число решений;
система имеет бесконечное число решений;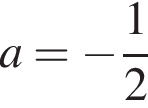 система имеет ровно одно решение;
система имеет ровно одно решение;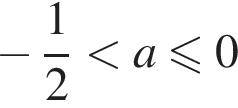 система не имеет решений;
система не имеет решений;

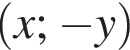 тоже является решением системы. Значит, нечетное число решение возможно только если одним из решений является пара чисел
тоже является решением системы. Значит, нечетное число решение возможно только если одним из решений является пара чисел 




 и
и  где
где  a
a  Тогда, исходная система имеет ровно пять решений:
Тогда, исходная система имеет ровно пять решений:





 тогда каждому значению
тогда каждому значению 
 Тогда исходная система тоже имеет ровно одно решение
Тогда исходная система тоже имеет ровно одно решение 


 если
если  то
то  если
если  и
и 

 при
при 

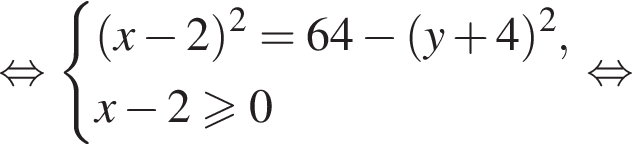
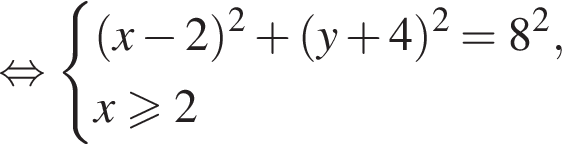


 радиусом 8 (выделена оранжевым).
радиусом 8 (выделена оранжевым). проходит через точку
проходит через точку  (выделено зелёным) при
(выделено зелёным) при 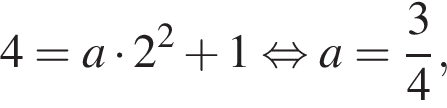
 (выделено синим) — при
(выделено синим) — при  то есть при
то есть при 
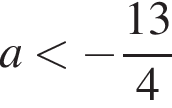 парабола и полуокружность не имеют общих точек, значит, исходная система не имеет решений, а при
парабола и полуокружность не имеют общих точек, значит, исходная система не имеет решений, а при  система имеет решения.
система имеет решения.



 графиком второго уравнения — точка
графиком второго уравнения — точка  Графиком второго уравнения исходной системы является семейство прямых
Графиком второго уравнения исходной системы является семейство прямых  Рассмотрим взаимное расположение графиков.
Рассмотрим взаимное расположение графиков. и
и 





 является касательной к параболе
является касательной к параболе 

 приравняв угловые коэффициенты. Получаем:
приравняв угловые коэффициенты. Получаем:  откуда
откуда  При
При 




 и
и 


 и
и  и
и  (см. рис.). Графиком уравнения второго уравнения исходной системы
(см. рис.). Графиком уравнения второго уравнения исходной системы  является пучок прямых, проходящих через точку A(4; 0) Число решений исходной системы равно числу точек пересечения прямых
является пучок прямых, проходящих через точку A(4; 0) Число решений исходной системы равно числу точек пересечения прямых  и
и  пересекает прямую
пересекает прямую  или если
или если  если
если  При
При  прямая
прямая 
 при
при  и при
и при 


 не являющееся решением первого уравнения. Значит,
не являющееся решением первого уравнения. Значит, 
 Складывая и вычитая это уравнение и уравнение
Складывая и вычитая это уравнение и уравнение  получим:
получим:
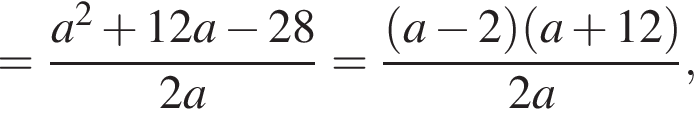
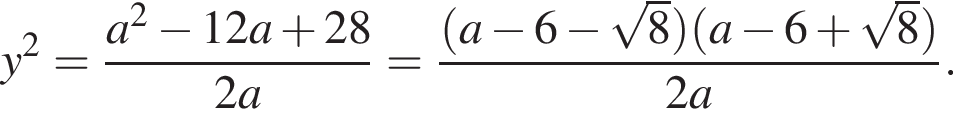

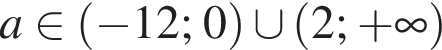 и
и  Значит, оба неравенства выполнены при
Значит, оба неравенства выполнены при 


 Это уравнение прямой, поэтому для существования двух решений требуется, чтобы она пересекала окружность
Это уравнение прямой, поэтому для существования двух решений требуется, чтобы она пересекала окружность  в двух точках. Это произойдет в том случае, когда расстояние от начала координат до этой прямой будет меньше радиуса окружности.
в двух точках. Это произойдет в том случае, когда расстояние от начала координат до этой прямой будет меньше радиуса окружности.  Следовательно, условие задачи выполнено тогда и только тогда, когда
Следовательно, условие задачи выполнено тогда и только тогда, когда 










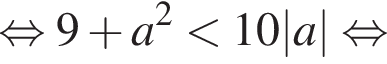
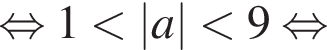
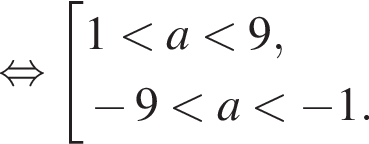






 с абсциссой 2 и положительной ординатой. Точка В — точка пересечения прямых
с абсциссой 2 и положительной ординатой. Точка В — точка пересечения прямых  и
и 


 где aA и aB — ординаты точек А и В соответственно. Таким образом, условие задачи выполнено при
где aA и aB — ординаты точек А и В соответственно. Таким образом, условие задачи выполнено при 






 и части гиперболы
и части гиперболы  лежащей не ниже этой прямой (выделено синим). Найдём точки пересечения прямой и гиперболы:
лежащей не ниже этой прямой (выделено синим). Найдём точки пересечения прямой и гиперболы:



 и
и 
 является семейство параллельных прямых с угловым коэффициентом 3, пересекающих ось ординат в точке
является семейство параллельных прямых с угловым коэффициентом 3, пересекающих ось ординат в точке  Прямая
Прямая  (выделено пурпурным) при
(выделено пурпурным) при 
 (выделено оранжевым) при
(выделено оранжевым) при 
 (выделено красным) при выполнении следующих условий:
(выделено красным) при выполнении следующих условий:
 прямая
прямая  при
при  — в точке
— в точке  Анализируя графики получаем, что исходная система:
Анализируя графики получаем, что исходная система: имеет одно решение;
имеет одно решение; — два решения;
— два решения; — три решения;
— три решения;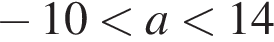 — одно решение;
— одно решение; — три решения.
— три решения.
 в первое уравнение. Получим
в первое уравнение. Получим  Заметим, что одним из корней полученного уравнения, будет
Заметим, что одним из корней полученного уравнения, будет  Далее возможны три варианта, в которых уравнение
Далее возможны три варианта, в которых уравнение 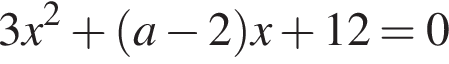 даст ровно один корень.
даст ровно один корень. положительно. Тогда дискриминант равен нулю, откуда
положительно. Тогда дискриминант равен нулю, откуда 


 а для второго выражение
а для второго выражение 



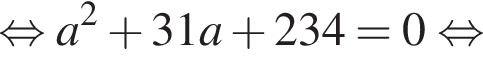

 с корнями
с корнями  и 4
и 4  —
— получаем уравнение
получаем уравнение  с корнями
с корнями  и
и  —
— лежит между корнями этого уравнения. То есть значение функции
лежит между корнями этого уравнения. То есть значение функции 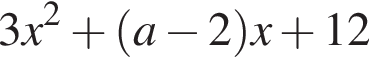 в точке
в точке  откуда
откуда 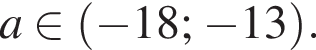



 Условие задачи будет выполнено тогда и только тогда, когда прямая
Условие задачи будет выполнено тогда и только тогда, когда прямая  лежит между прямой
лежит между прямой  (выделено красным) и прямой
(выделено красным) и прямой  являющейся касательной к окружности (выделено синим), то есть при
являющейся касательной к окружности (выделено синим), то есть при  Решим полученное двойное неравенство:
Решим полученное двойное неравенство: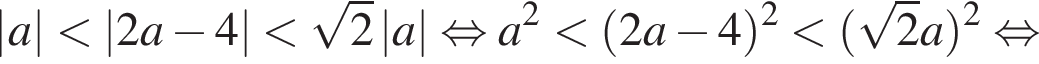


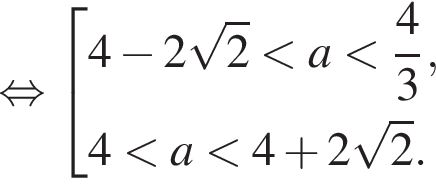


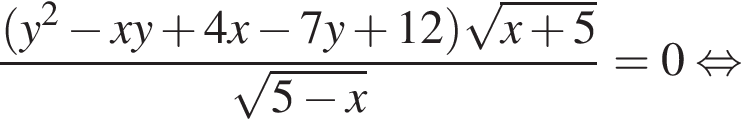


 и отрезков двух прямых с открытым концом (выделено оранжевым).
и отрезков двух прямых с открытым концом (выделено оранжевым). 

 графики не пересекаются.
графики не пересекаются. ).
). (выделено пурпурным) графики имеют ровно две общие точки, значит, система имеет ровно два различных решения.
(выделено пурпурным) графики имеют ровно две общие точки, значит, система имеет ровно два различных решения. графики имеют более двух общих точек, значит, система имеет более двух различных решений (от трёх до шести различных решений).
графики имеют более двух общих точек, значит, система имеет более двух различных решений (от трёх до шести различных решений). (выделено зелёным) и
(выделено зелёным) и  графики имеют ровно две общие точки, значит, система имеет ровно два различных решения.
графики имеют ровно две общие точки, значит, система имеет ровно два различных решения.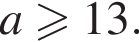




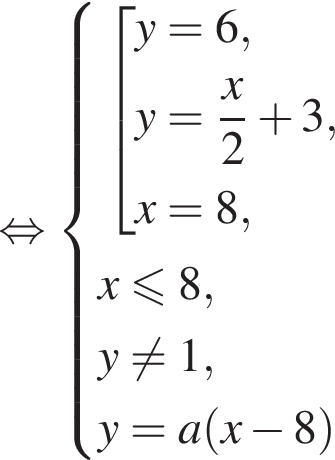

 пересекаются в точке
пересекаются в точке  Графиком последнего уравнения является пучок прямых, проходящих через точку
Графиком последнего уравнения является пучок прямых, проходящих через точку  проходит через точку
проходит через точку  при
при  (выделено синим). При
(выделено синим). При  система имеет ровно три решения;
система имеет ровно три решения; система имеет ровно три решения;
система имеет ровно три решения; система имеет ровно два решения;
система имеет ровно два решения;
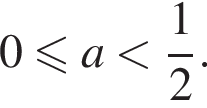


 и
и  они разбивают координатную плоскость на четыре области, в каждой их которых стоящие под знаком модуля выражения сохраняют знак. Взяв пробные точки в полученных областях, снимаем знаки модулей:
они разбивают координатную плоскость на четыре области, в каждой их которых стоящие под знаком модуля выражения сохраняют знак. Взяв пробные точки в полученных областях, снимаем знаки модулей:



 является прямоугольник с вершинами в точках
является прямоугольник с вершинами в точках 




 радиусом
радиусом  при
при  окружность
окружность  Окружность
Окружность 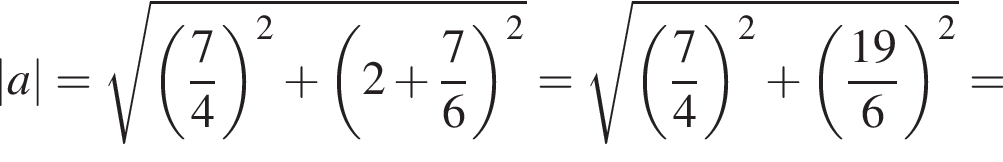

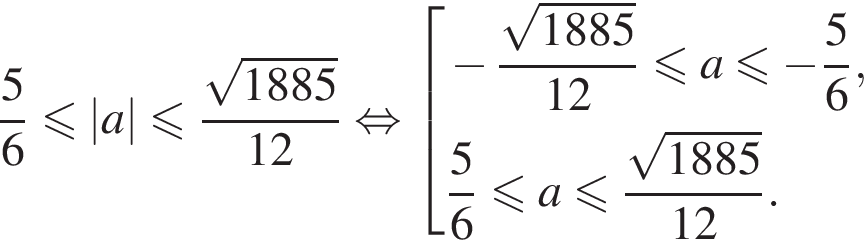






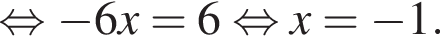





 являются решениями уравнения.
являются решениями уравнения.





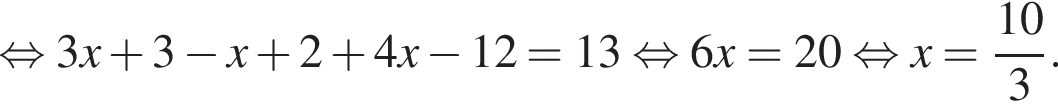



 равна
равна  а их произведение равно
а их произведение равно  По теореме, обратной теореме Виета, корнями этого уравнения являются числа
По теореме, обратной теореме Виета, корнями этого уравнения являются числа  Эти числа различны для всех значений параметра. Чтобы систем имела два различных решения, необходимо и достаточно, чтобы найденные корни одновременно принадлежали множеству решений первого уравнения:
Эти числа различны для всех значений параметра. Чтобы систем имела два различных решения, необходимо и достаточно, чтобы найденные корни одновременно принадлежали множеству решений первого уравнения: