
Через вершины A и B треугольника ABC проведена окружность, касающаяся прямой BC, а через вершины B и C — другая окружность, касающаяся прямой AB. Продолжение общей хорды BD этих окружностей пересекает отрезок AC в точке E, а продолжение хорды AD одной окружности пересекает другую окружность в точке F.
а) Доказать, что площади треугольников ABC и ABF равны.
б) Найти отношение AE : EC, если AB = 5 и BC = 9.
Решение. Окружность с центром в O1 будем называть первой окружностью, с центром в O2 — второй окружностью.
а) У треугольников ABC и ABF общее основание AB. Значит, для равенства площадей надо доказать равенство их высот, опущенных из вершин C и F соответственно. Следовательно, надо доказать параллельность прямых AB и FC: это можно получить, если вывести равенство углов ∠AFC и ∠BAF (накрест лежащие).
Во-первых, во второй окружности углы ∠DBC и ∠DFC равны, так как они опираются на одну и ту же дугу DC.
Во-вторых, угол между касательной к окружности и хордой равен половине дуги, опирающейся на эту хорду. Тогда из первой окружности получим, что  (вписанный угол равен половине центрального). Таким образом, получили, что ∠BAF = ∠AFC, то есть AB || FC, значит, высоты треугольников равны, и их площади совпадают.
(вписанный угол равен половине центрального). Таким образом, получили, что ∠BAF = ∠AFC, то есть AB || FC, значит, высоты треугольников равны, и их площади совпадают.
Что и требовалось доказать.
б) Аналогично углам ∠BAD и ∠BDC получаем, что ∠ABD = ∠BCD (угол ∠ABD между касательной ко второй окружности и хордой BD равен углу ∠BCD, опирающемуся на эту хорду). Таким образом, получаем, что ΔABD ~ ΔBCD (по 2 углам). Так как ∠ADB = ∠BDC = α, то ∠ADE = π − α, ∠CDE = π − α, то есть ∠ADE = ∠CDE, откуда следует, что DE — биссектриса треугольника ADC. Тогда из свойства биссектрисы имеем соотношение
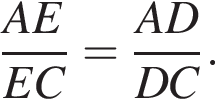
Теперь воспользуемся подобием треугольников ABD и BCD:

Из второго равенства выше выразим BD:  Подставим это в первое равенство:
Подставим это в первое равенство:



Окончательно получаем, что 
Ответ: 25 : 81.
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б. | 3 |
| Получен обоснованный ответ в пункте б. ИЛИ Имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. | 2 |
| Имеется верное доказательство утверждения пункта а. ИЛИ При обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. ИЛИ Обоснованно получен верный ответ в пункте б и использованием утверждения пункта а, при этом пункт а не выполнен. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 3 |
 Из свойств касательной и секущей к окружности получим:
Из свойств касательной и секущей к окружности получим:




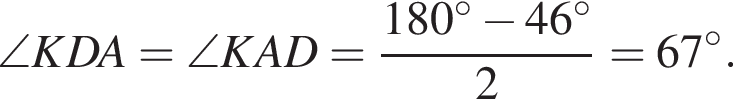
 то есть OK — биссектриса угла AOD. Вписанный угол ACD опирается на дугу AD и равен половине центрального угла AOD, то есть
то есть OK — биссектриса угла AOD. Вписанный угол ACD опирается на дугу AD и равен половине центрального угла AOD, то есть  Что и требовалось доказать.
Что и требовалось доказать.





 Проведём отрезок A1B1 через точку E так, чтобы A1B1 был параллелен AB. В трапеции A1ABB1 по свойству углов, прилежащих к боковой стороне,
Проведём отрезок A1B1 через точку E так, чтобы A1B1 был параллелен AB. В трапеции A1ABB1 по свойству углов, прилежащих к боковой стороне,  По признаку вписанного четырехугольника ABCD
По признаку вписанного четырехугольника ABCD  следовательно:
следовательно:
 и
и 












 тогда A1D = B1C как соответствующие элементы. Треугольники A1DE и ECB1 равны по двум углам и стороне
тогда A1D = B1C как соответствующие элементы. Треугольники A1DE и ECB1 равны по двум углам и стороне 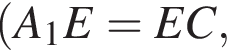
 тогда EB1 = DE как соответствующие элементы.
тогда EB1 = DE как соответствующие элементы. 





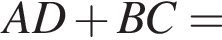




















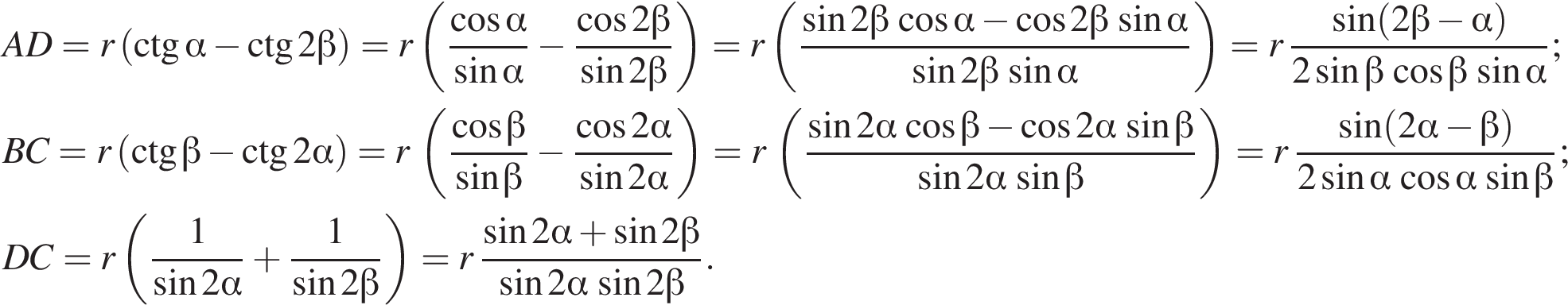



 откуда получим:
откуда получим:






 Тогда:
Тогда:










 Так как треугольник AO2B равнобедренный (AO2 = O2B = R1), то
Так как треугольник AO2B равнобедренный (AO2 = O2B = R1), то





 а значит точка O лежит на стороне AB. Лемма доказана.
а значит точка O лежит на стороне AB. Лемма доказана.

 и треугольники AEC и EBC подобны по 2-м углам, откуда выпишем соотношения:
и треугольники AEC и EBC подобны по 2-м углам, откуда выпишем соотношения:










 Так как вписанный угол KAM и центральный угол KOM опираются на одну и ту же дугу KM в окружности
Так как вписанный угол KAM и центральный угол KOM опираются на одну и ту же дугу KM в окружности  В четырехугольнике ACLB углы ACL и ABL равны по
В четырехугольнике ACLB углы ACL и ABL равны по 



 Что и требовалось доказать.
Что и требовалось доказать.

 Вписанный угол BDA опирается на ту же дугу BA, что и центральный угол AQB. Тогда
Вписанный угол BDA опирается на ту же дугу BA, что и центральный угол AQB. Тогда  Далее, в меньшей окружности с центром O рассмотрим центральный угол
Далее, в меньшей окружности с центром O рассмотрим центральный угол  изображенный синим на рисунке, который опирается на бОльшую дугу AB. На эту же дугу опирается вписанный угол
изображенный синим на рисунке, который опирается на бОльшую дугу AB. На эту же дугу опирается вписанный угол  который в 2 раза меньше центрального. Тогда:
который в 2 раза меньше центрального. Тогда:





 так как треугольник AQD равнобедренный;
так как треугольник AQD равнобедренный;  как вертикальные
как вертикальные







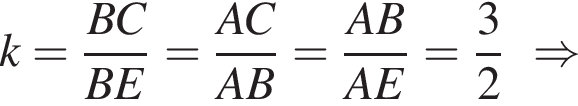


 Отметим на продолжении луча KC за точку C произвольную точку L. Тогда треугольник ACD также равнобедренный, в нем медиана совпадает с высотой. Значит,
Отметим на продолжении луча KC за точку C произвольную точку L. Тогда треугольник ACD также равнобедренный, в нем медиана совпадает с высотой. Значит,  тогда и соответствующие дуги равны. Тогда
тогда и соответствующие дуги равны. Тогда  поскольку один из них вписанный, опирающийся на дугу AD, а второй — угол между касательной и хордой, стягивающей дугу AC.
поскольку один из них вписанный, опирающийся на дугу AD, а второй — угол между касательной и хордой, стягивающей дугу AC. как соответственные углы при пересечении параллельных прямых KB и CD (они обе перпендикулярны AB) секущей KL. Кроме того KO — биссектриса угла BKC, потому что проходит через центр окружности, а стороны угла — касательные из одной точки. Поэтому
как соответственные углы при пересечении параллельных прямых KB и CD (они обе перпендикулярны AB) секущей KL. Кроме того KO — биссектриса угла BKC, потому что проходит через центр окружности, а стороны угла — касательные из одной точки. Поэтому  откуда прямоугольные треугольники BKO и ECA подобны по двум углам.
откуда прямоугольные треугольники BKO и ECA подобны по двум углам. Из треугольника OEC находим
Из треугольника OEC находим  Тогда
Тогда 
 откуда
откуда 


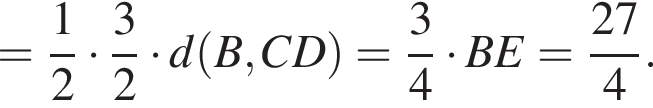


 (поскольку один из них вписанный, опирающийся на дугу AC, а второй — угол между касательной и хордой, стягивающей дугу AC). Значит, в прямоугольных треугольниках AKC и MBC есть одинаковые острые углы, поэтому они подобны по двум углам.
(поскольку один из них вписанный, опирающийся на дугу AC, а второй — угол между касательной и хордой, стягивающей дугу AC). Значит, в прямоугольных треугольниках AKC и MBC есть одинаковые острые углы, поэтому они подобны по двум углам. откуда следует второе указанное в условии подобие.
откуда следует второе указанное в условии подобие.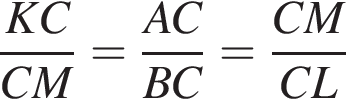 (первое равенство — из подобия AKC и MBC, второе — из подобия AMC и BLC). Приравнивая крайние отношения, находим
(первое равенство — из подобия AKC и MBC, второе — из подобия AMC и BLC). Приравнивая крайние отношения, находим  откуда
откуда 
 лежат на одной прямой. Обозначим за R радиус большей окружности. Тогда
лежат на одной прямой. Обозначим за R радиус большей окружности. Тогда 


 откуда
откуда 

 ), поэтому для поиска его площади достаточно найти его катеты:
), поэтому для поиска его площади достаточно найти его катеты:





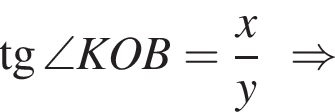


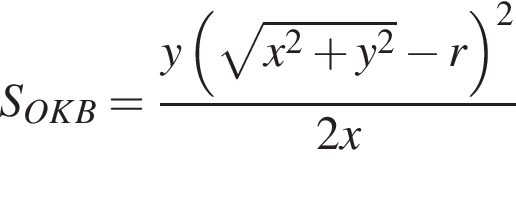 или
или 
 Это значит, что
Это значит, что  BO = CO как радиусы одной и той же окружности.
BO = CO как радиусы одной и той же окружности. проведенной к ВС, будет Н. Тогда
проведенной к ВС, будет Н. Тогда  Кроме того,
Кроме того,  значит,
значит,  OH = BH = 2.
OH = BH = 2.

 т. е.
т. е. 
 и
и 



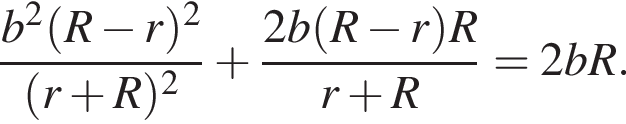











 т. е.
т. е. 














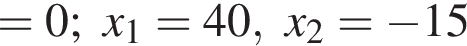














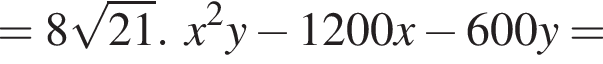







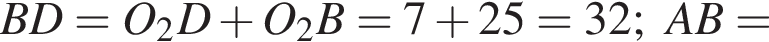




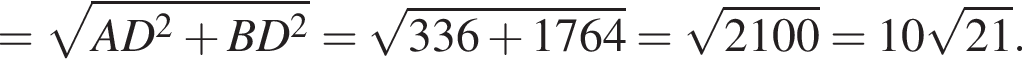
















 В четырехугольник ONCM вписана окружность.
В четырехугольник ONCM вписана окружность.

 Аналогично
Аналогично 
 как дополняющие равные вертикальные углы AOC и FON до
как дополняющие равные вертикальные углы AOC и FON до  Отсюда:
Отсюда: 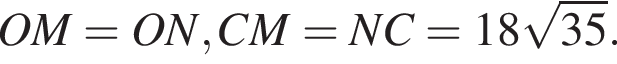

 получим:
получим: 
 Так как
Так как  то
то 
 как вертикальные, OM = ON по выше доказанному.
как вертикальные, OM = ON по выше доказанному. 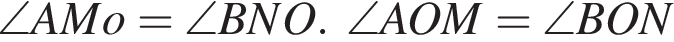 как вертикальные. Значит,
как вертикальные. Значит,  по второму признаку равенства треугольников, откуда
по второму признаку равенства треугольников, откуда 


 Значит,
Значит,  следовательно,
следовательно, 
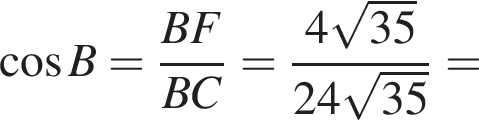


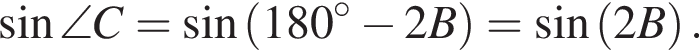
















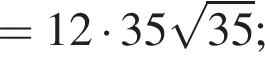









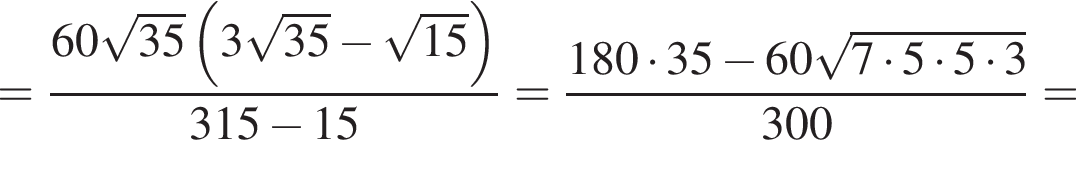








 Тогда
Тогда  (поскольку
(поскольку  так как
так как 

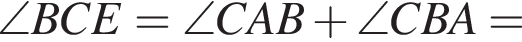



 значит, C — середина AE.
значит, C — середина AE.













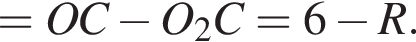
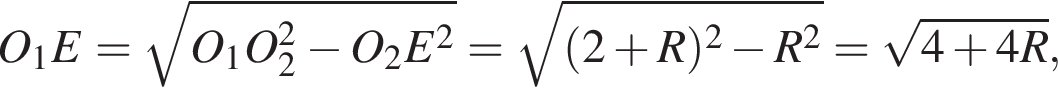

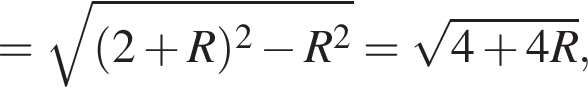





 (O лежит между E и O1) и
(O лежит между E и O1) и  (E лежит между O и O1). Это дает нам два уравнения
(E лежит между O и O1). Это дает нам два уравнения  и
и  которые имеют общее решение R = 3, это означает, что диаметр искомой окружности равен радиусу наибольшей из трёх окружностей, что точка E совпадает с O.
которые имеют общее решение R = 3, это означает, что диаметр искомой окружности равен радиусу наибольшей из трёх окружностей, что точка E совпадает с O.
 тогда
тогда 




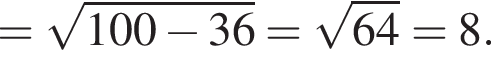










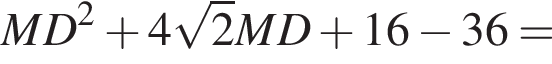



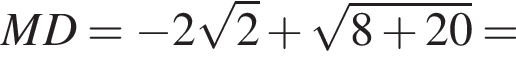













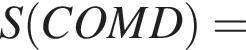


















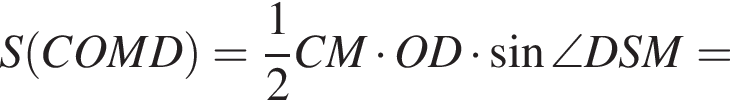


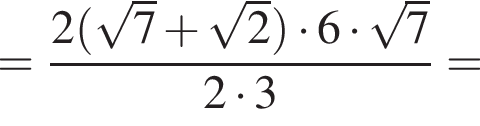
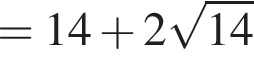




 Следовательно, AEOK — параллелограмм, откуда AE = OK = R. Но AE = AK как отрезки касательных к окружности, проведенных из точки А. Следовательно, AK = AE = R. В таком случае KD = 18 − R.
Следовательно, AEOK — параллелограмм, откуда AE = OK = R. Но AE = AK как отрезки касательных к окружности, проведенных из точки А. Следовательно, AK = AE = R. В таком случае KD = 18 − R.






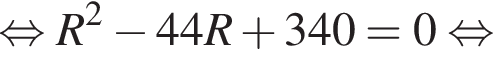























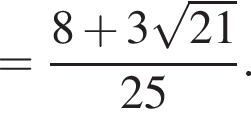









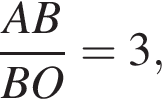 значит,
значит,  Выше было получено:
Выше было получено:  Тогда:
Тогда: 

 (опираются на диаметр AO меньшей окружности), а треугольники AOC и AOB равнобедренные, то OM и OP — медианы этих треугольников (поскольку являются высотами). Тогда M и P — середины отрезков AC и AB, а MP — средняя линия треугольника ABC и параллельна его основанию.
(опираются на диаметр AO меньшей окружности), а треугольники AOC и AOB равнобедренные, то OM и OP — медианы этих треугольников (поскольку являются высотами). Тогда M и P — середины отрезков AC и AB, а MP — средняя линия треугольника ABC и параллельна его основанию. Обозначим центр меньшей окружности за
Обозначим центр меньшей окружности за 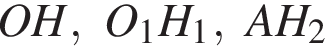 на BC. Тогда H — середина BC и поэтому
на BC. Тогда H — середина BC и поэтому 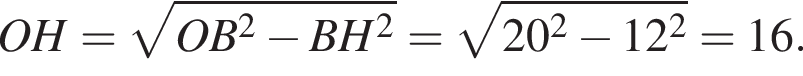


 поскольку хорда касается меньшей окружности.
поскольку хорда касается меньшей окружности. — прямоугольная трапеция, в которой
— прямоугольная трапеция, в которой 













 откуда
откуда  Тогда
Тогда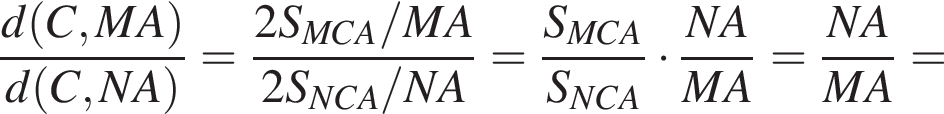







 откуда
откуда 

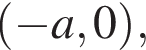 тогда
тогда  и
и  а их радиусы — a и
а их радиусы — a и  Пусть центр окружности, касающейся правой полуокружности, имеет координаты
Пусть центр окружности, касающейся правой полуокружности, имеет координаты  и
и 

 получаем
получаем  то есть
то есть 

 — прямоугольная трапеция, в которой
— прямоугольная трапеция, в которой 

 и (опуская высоту из
и (опуская высоту из  откуда
откуда  — трапеция, в которой
— трапеция, в которой  откуда
откуда  Кроме того,
Кроме того,  откуда
откуда  аналогично
аналогично  и расстояние между хордами
и расстояние между хордами 
 В ней
В ней  а высота
а высота  При этом
При этом  откуда
откуда 
 то
то  и поэтому
и поэтому 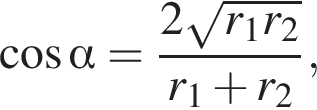
 Наконец, расстояние между хордами
Наконец, расстояние между хордами
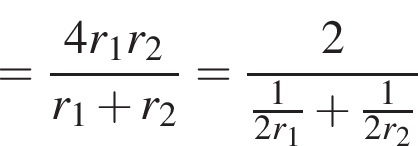


 аналогично
аналогично  поэтому их полусумма составит
поэтому их полусумма составит 



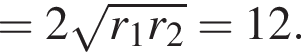
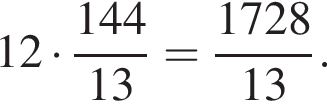

 Пусть
Пусть  тогда
тогда 
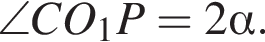

 поэтому
поэтому  Обозначим
Обозначим тогда
тогда

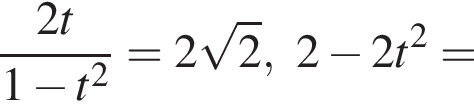






 Очевидно,
Очевидно,  так как AC — диаметр. Значит, треугольники AKC и
так как AC — диаметр. Значит, треугольники AKC и 


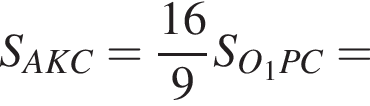


 Будем считать, что
Будем считать, что 

 Очевидно, C — середина
Очевидно, C — середина  ). Поэтому
). Поэтому  и ABC — равнобедренный.
и ABC — равнобедренный.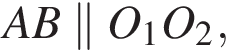 и треугольники
и треугольники 





 и, значит,
и, значит, 
 из-за равенства слагаемых).
из-за равенства слагаемых). 




 Запишем тогда теорему косинусов для треугольников OCK и OCP.
Запишем тогда теорему косинусов для треугольников OCK и OCP.
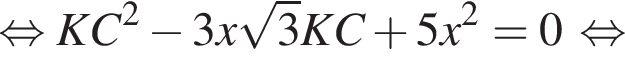

 при этом PC > KC.
при этом PC > KC. а поскольку
а поскольку  находим
находим 
 поскольку
поскольку 







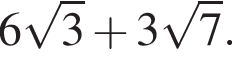




 поэтому K — точка касания вписанной окружности треугольника ABC со стороной AB. Аналогично и точки M и P. Поэтому нам нужно найти радиус вписанной окружности треугольника ABC. Он равен
поэтому K — точка касания вписанной окружности треугольника ABC со стороной AB. Аналогично и точки M и P. Поэтому нам нужно найти радиус вписанной окружности треугольника ABC. Он равен 
 (в большой окружности один из них вписанный, а другой — угол между касательной и хордой, поэтому они оба равны половине дуги BK) и
(в большой окружности один из них вписанный, а другой — угол между касательной и хордой, поэтому они оба равны половине дуги BK) и  (поскольку
(поскольку  как отрезки касательных к маленькой окружности). Тогда
как отрезки касательных к маленькой окружности). Тогда

 и, следовательно,
и, следовательно, 
 и
и 







 Итак, этот треугольник прямоугольный, поэтому его высота, опущенная на гипотенузу, равна произведению катетов, деленному на гипотенузу (это следует из формул для площади треугольника).
Итак, этот треугольник прямоугольный, поэтому его высота, опущенная на гипотенузу, равна произведению катетов, деленному на гипотенузу (это следует из формул для площади треугольника). высота MN равна
высота MN равна 
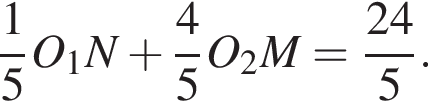 Значит, площадь треугольника равна
Значит, площадь треугольника равна 
 Тогда
Тогда 








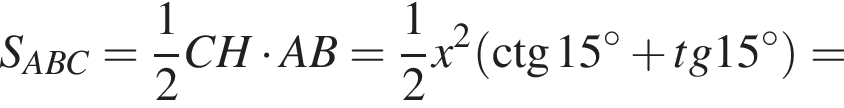



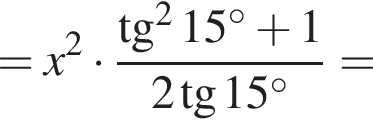
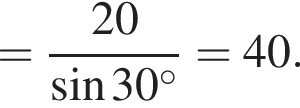























 Поэтому:
Поэтому:




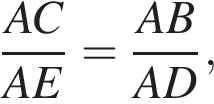

 Поскольку окружности касаются прямой AC, прямая
Поскольку окружности касаются прямой AC, прямая 











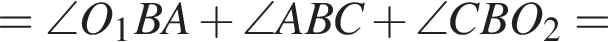


 имеем:
имеем: 
 высоту
высоту 












 и окончательный ответ
и окончательный ответ 



 тогда
тогда 
 Обозначим за I центр вписанной окружности, тогда
Обозначим за I центр вписанной окружности, тогда 
 тогда
тогда 
 и
и 



 Пусть
Пусть 
 тогда по теореме синусов для треугольника FGH получаем:
тогда по теореме синусов для треугольника FGH получаем:
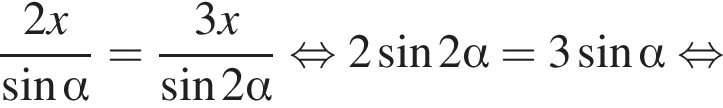



 и угол
и угол  существует. В этом случае
существует. В этом случае 



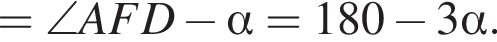

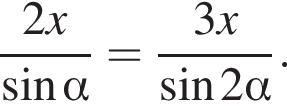 Это то же самое уравнение, что и в случае 1, поэтому
Это то же самое уравнение, что и в случае 1, поэтому  поэтому
поэтому  не существует. Поэтому такой случай невозможен.
не существует. Поэтому такой случай невозможен.
 (лемма о касательной и хорде). Заметим, что точки A, B1, A1 и B лежат на окружности с центром N. Значит,
(лемма о касательной и хорде). Заметим, что точки A, B1, A1 и B лежат на окружности с центром N. Значит, 
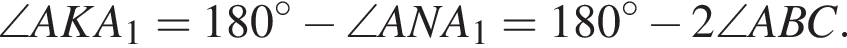









 то
то 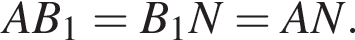 Следовательно, треугольник AB1N равносторонний. Значит,
Следовательно, треугольник AB1N равносторонний. Значит, 
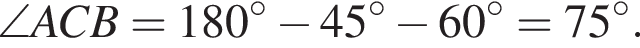 Далее,
Далее, 
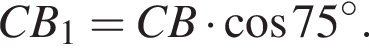 Значит, треугольники A1B1C и ABC подобны с
Значит, треугольники A1B1C и ABC подобны с  Далее:
Далее:







 Далее,
Далее,
 Поэтому ABCD — ромб.
Поэтому ABCD — ромб. Имеем:
Имеем:  откуда
откуда
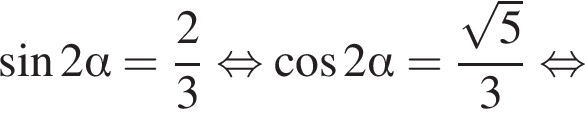





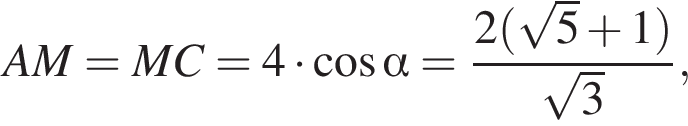







 (отрезки касательных), поэтому
(отрезки касательных), поэтому  Пусть
Пусть 
 тогда
тогда  Треугольники AOG и ADB подобны,
Треугольники AOG и ADB подобны,  тогда
тогда

 тогда
тогда

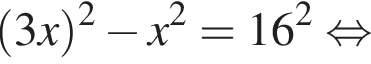


 Теперь найдём площадь четырехугольника AODQ:
Теперь найдём площадь четырехугольника AODQ:








 Далее,
Далее,  тогда
тогда 
 Найдем сторону ромба:
Найдем сторону ромба:

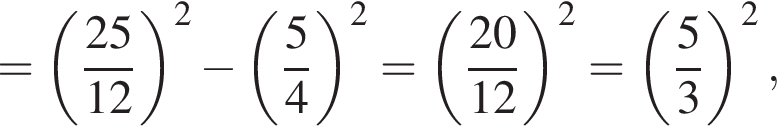










 так как сумма вписанных углов равна половине суммы третей дуг AB, BC, AC, то есть
так как сумма вписанных углов равна половине суммы третей дуг AB, BC, AC, то есть  Аналогично вычисляются и углы KDE и KED. Таким образом, все углы треугольника KDE равны между собой. Поэтому он равносторонний.
Аналогично вычисляются и углы KDE и KED. Таким образом, все углы треугольника KDE равны между собой. Поэтому он равносторонний. Отсюда ясно, что диаметр окружности равен 2, а радиус 1. Таким образом, дуга BA равна 60°, дуга AC = 120°, дуга CB — полуокружность (обозначим центр окружности через O). Отсюда легко определяются все дуги, на которые 9 точек делят окружность. Сделаем дополнительное построение, проведя диаметр GH, где G — середина дуги AC2. Заметим, что хорда A2C1 опирается на угол 120°, значит, она равна
Отсюда ясно, что диаметр окружности равен 2, а радиус 1. Таким образом, дуга BA равна 60°, дуга AC = 120°, дуга CB — полуокружность (обозначим центр окружности через O). Отсюда легко определяются все дуги, на которые 9 точек делят окружность. Сделаем дополнительное построение, проведя диаметр GH, где G — середина дуги AC2. Заметим, что хорда A2C1 опирается на угол 120°, значит, она равна  Кроме того эта хорда перпендикулярна диаметру GH, поэтому она делится им пополам (точку пересечения хорды и диаметра обозначим M). Заметим еще, что B2KC2 — равнобедренный треугольник (углы при его основании опираются на равные дуги), причем B2C2 параллельно HG. Поэтому KO и GH перпендикулярны. Наконец, заметим, что OA2GC1 — ромб. Рассмотрим теперь прямоугольную трапецию KOMD. В ней боковая сторона OM равна 0,5, а острый угол равен 60°. Тогда вторая боковая сторона (KD) равна
Кроме того эта хорда перпендикулярна диаметру GH, поэтому она делится им пополам (точку пересечения хорды и диаметра обозначим M). Заметим еще, что B2KC2 — равнобедренный треугольник (углы при его основании опираются на равные дуги), причем B2C2 параллельно HG. Поэтому KO и GH перпендикулярны. Наконец, заметим, что OA2GC1 — ромб. Рассмотрим теперь прямоугольную трапецию KOMD. В ней боковая сторона OM равна 0,5, а острый угол равен 60°. Тогда вторая боковая сторона (KD) равна 