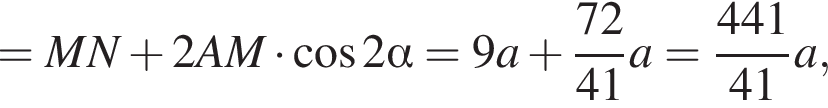Диагональ AC прямоугольника ABCD с центром O образует со стороной AB угол 30°. Точка E лежит вне прямоугольника, причём ∠BEC = 120°.
а) Докажите, что ∠CBE = ∠COE.
б) Прямая OE пересекает сторону AD прямоугольника в точке K. Найдите EK, если известно, что BE = 40 и CE = 24.
Решение. а) По теореме о внешнем угле треугольника,
∠BOC = ∠BAO + ∠АBO = 2 · 30° = 60°.
Поэтому

Значит, точки B, E, C, O лежат на одной окружности. Вписанные в эту окружность углы CBE и COE опираются на одну и ту же дугу, следовательно, ∠CBE = ∠COE.
б) По теореме косинусов



![]()



Вписанные углы BEO и CEO опираются на равные хорды BO и CO, значит, EO — биссектриса угла BEC. Пусть M — точка её пересечения со стороной BC. По формуле для биссектрисы треугольника получаем:



По свойству биссектрисы треугольника  значит,
значит, 
По теореме о произведении пересекающихся хорд EM · MO = BM · CM, откуда находим, что

Треугольники COM и AOK равны по стороне и двум прилежащим к ней углам, поэтому OK = OM. Следовательно, EK = EM + 2OM = 15 + 98 = 113.
Ответ: 113.
Примечание.
Зная длину отрезка СМ = 21, можно искать ME, применяя теорему косинусов к треугольнику СМЕ. Пусть в нем МЕ = х, тогда





Поскольку треугольник СМЕ остроугольный, решение х = 9 постороннее. Посторонние корни появляются из-за того, что по стороне, прилежащему к ней углу и противолежащей данному углу стороне треугольник определен неоднозначно. Аналогично для треугольника BME: можно найти два корня уравнения на длину EM: 15 и 25, больший корень является посторонним.
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) ИЛИ имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) ИЛИ при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | 1 |
| Решение не соответствует ни одному из критериев, приведённых выше | 0 |
| Максимальный балл | 3 |













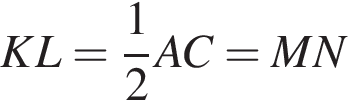 и KL || AC || MN, поэтому KLMN — параллелограмм. Его диагонали KM и LN делят друг друга пополам, что и требовалось доказать.
и KL || AC || MN, поэтому KLMN — параллелограмм. Его диагонали KM и LN делят друг друга пополам, что и требовалось доказать.



 поэтому треугольник KLM прямоугольный треугольник с прямым углом при вершине L. Четырёхугольник KLMN — прямоугольник, поэтому
поэтому треугольник KLM прямоугольный треугольник с прямым углом при вершине L. Четырёхугольник KLMN — прямоугольник, поэтому
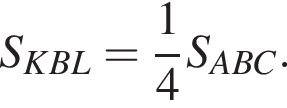 Аналогично
Аналогично  Тогда имеем:
Тогда имеем:
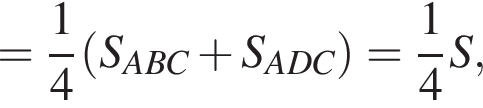


 Поэтому
Поэтому

 KL || AC, LM || BD, тогда
KL || AC, LM || BD, тогда  Следовательно,
Следовательно,





 Из доказанного следует, что BP = PR = RM.
Из доказанного следует, что BP = PR = RM.


 Пусть RM = y, тогда BR = 2y, BM = 3y.
Пусть RM = y, тогда BR = 2y, BM = 3y. Пусть BP = z, тогда PM = 2z, BM = 3z.
Пусть BP = z, тогда PM = 2z, BM = 3z. Найдём площадь треугольника BNL. Из подобия треугольников BPN и MPA следует, что
Найдём площадь треугольника BNL. Из подобия треугольников BPN и MPA следует, что





 как вписанные,
как вписанные,  по сумме углов треугольника,
по сумме углов треугольника,  из параллельности BE и CF. Следовательно, CO — биссектриса угла BCF, значит,
из параллельности BE и CF. Следовательно, CO — биссектриса угла BCF, значит,  Аналогично, BO — биссектриса угла CBE, а значит, прямые CE и BF перпендикулярны и делятся точкой O пополам, следовательно, CBEF — ромб. Что требовалось доказать.
Аналогично, BO — биссектриса угла CBE, а значит, прямые CE и BF перпендикулярны и делятся точкой O пополам, следовательно, CBEF — ромб. Что требовалось доказать.
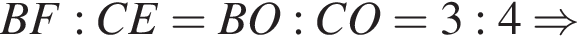

 Пусть OH — высота треугольника BOC, значит,
Пусть OH — высота треугольника BOC, значит,  Следовательно,
Следовательно, 




 как накрест лежащие при пересечении параллельных прямых секущей,
как накрест лежащие при пересечении параллельных прямых секущей,  как углы равнобедренного треугольника BMD. Значит,
как углы равнобедренного треугольника BMD. Значит,  Далее имеем:
Далее имеем: 
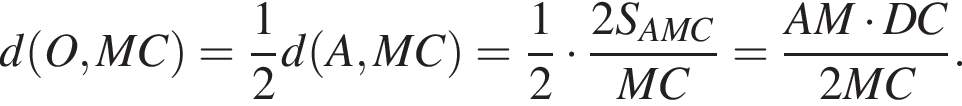


 откуда
откуда  Далее
Далее 
 Поэтому
Поэтому


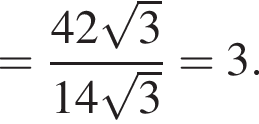

 откуда
откуда
 Значит, ABCK — прямоугольник.
Значит, ABCK — прямоугольник.









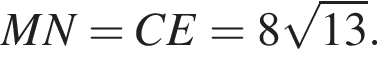
 откуда находим:
откуда находим:







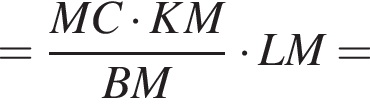









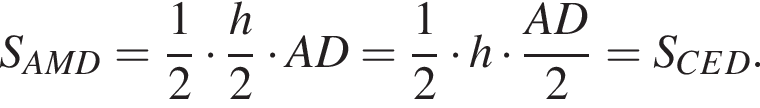



 как накрест лежащие при параллельных прямых KC и AD и секущей AB,
как накрест лежащие при параллельных прямых KC и AD и секущей AB,  как вертикальные, AM = BM. Значит, треугольники AMD и BMK равны, откуда BK = AD = 4.
как вертикальные, AM = BM. Значит, треугольники AMD и BMK равны, откуда BK = AD = 4. как накрест лежащие при параллельных прямых KC и AD и секущей CE. Значит, треугольники KOC и DOE подобны по двум углам, откуда
как накрест лежащие при параллельных прямых KC и AD и секущей CE. Значит, треугольники KOC и DOE подобны по двум углам, откуда  Следовательно,
Следовательно,




 откуда по теореме, обратной теореме о пропорциональных отрезках, заключаем, что прямые BH и ED параллельны.
откуда по теореме, обратной теореме о пропорциональных отрезках, заключаем, что прямые BH и ED параллельны. Далее имеем:
Далее имеем: 







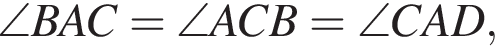 следовательно, AC — биссектриса угла BAD.
следовательно, AC — биссектриса угла BAD. Из прямоугольного треугольника CAE находим, что
Из прямоугольного треугольника CAE находим, что  Следовательно, CD = AE = 8.
Следовательно, CD = AE = 8.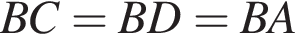 были ее радиусами. Тогда углы BCA и CAD равны как накрест лежащие, а углы BCA и BAC равны, поскольку треугольник ABC равнобедренный. Получаем:
были ее радиусами. Тогда углы BCA и CAD равны как накрест лежащие, а углы BCA и BAC равны, поскольку треугольник ABC равнобедренный. Получаем:  то есть AC — биссектриса угла BAD.
то есть AC — биссектриса угла BAD.

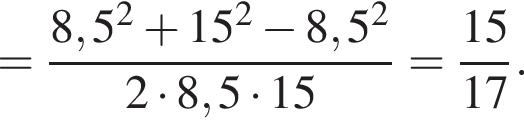
 По теореме синусов:
По теореме синусов:











 и четырехугольник KCLA — трапеция. Прямая BE содержит точку пересечения боковых сторон трапеции и середину ее основания AL. Тогда по замечательному свойству трапеции она содержит и середину основания КС — точку O. Таким образом,
и четырехугольник KCLA — трапеция. Прямая BE содержит точку пересечения боковых сторон трапеции и середину ее основания AL. Тогда по замечательному свойству трапеции она содержит и середину основания КС — точку O. Таким образом, 
 Из подобия треугольников KBC и ABL следует, что
Из подобия треугольников KBC и ABL следует, что 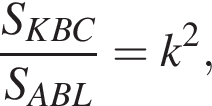 то есть
то есть  Тогда
Тогда 
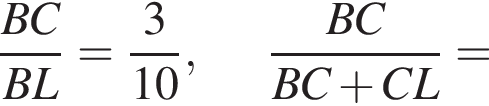



 Треугольники LBE и CBO подобны с тем же коэффициентом подобия. Тогда
Треугольники LBE и CBO подобны с тем же коэффициентом подобия. Тогда 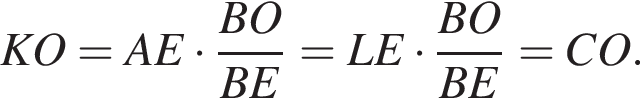
 поэтому BC — средняя линия треугольника AQD, тогда
поэтому BC — средняя линия треугольника AQD, тогда  Углы MCD и MBA прямые, из чего следует, что MC и MB — медианы и высоты, тогда треугольники QMD и QMA равнобедренные, то есть
Углы MCD и MBA прямые, из чего следует, что MC и MB — медианы и высоты, тогда треугольники QMD и QMA равнобедренные, то есть  а значит,
а значит,  что и требовалось доказать.
что и требовалось доказать.

 тогда
тогда  MN — медиана,
MN — медиана,  поэтому угол
поэтому угол  Треугольник MND прямоугольный и равнобедренный, тогда
Треугольник MND прямоугольный и равнобедренный, тогда  Заметим теперь, что
Заметим теперь, что 
 Имеем:
Имеем:
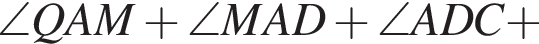
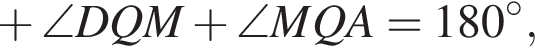
 Тогда
Тогда 

 откуда
откуда 


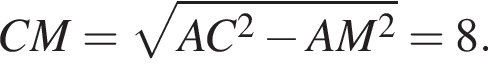 Треугольники BCO и MOD равны, поскольку
Треугольники BCO и MOD равны, поскольку  угол CBO равен углу ODM, а угол C равен углу M. Тогда
угол CBO равен углу ODM, а угол C равен углу M. Тогда  откуда O — середина BD, CO — искомое расстояние. Из равенства треугольников BCO и MOD следует равенство отрезков CO и OM, откуда
откуда O — середина BD, CO — искомое расстояние. Из равенства треугольников BCO и MOD следует равенство отрезков CO и OM, откуда 
 откуда CD = 10. В треугольнике BCD точка О — середина отрезка BD, поэтому CO — медиана. Найдем ее длину по формуле длины медианы:
откуда CD = 10. В треугольнике BCD точка О — середина отрезка BD, поэтому CO — медиана. Найдем ее длину по формуле длины медианы:
 — параллелограмм.
— параллелограмм. 


 поскольку
поскольку  тогда по теореме, обратной теореме Пифагора, треугольник ACC1 прямоугольный, угол ACC1 прямой. Тогда угол COD прямой, что и требовалось доказать.
тогда по теореме, обратной теореме Пифагора, треугольник ACC1 прямоугольный, угол ACC1 прямой. Тогда угол COD прямой, что и требовалось доказать.
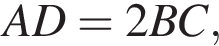 и точка M внутри трапеции, такая, что
и точка M внутри трапеции, такая, что 
 MN — медиана, откуда
MN — медиана, откуда 
 Имеем:
Имеем: Тогда
Тогда 






 Его положительным корнем является AH = 0,5, и тогда AD = 8.
Его положительным корнем является AH = 0,5, и тогда AD = 8. откуда получаем
откуда получаем  или
или 



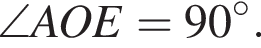


 Аналогично треугольник EOC — равнобедренный, в нем
Аналогично треугольник EOC — равнобедренный, в нем  поэтому
поэтому  Треугольники AOD и COD равны по трем сторонам, поэтому
Треугольники AOD и COD равны по трем сторонам, поэтому  а значит, точка O лежит на диагонали BD.
а значит, точка O лежит на диагонали BD.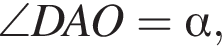 тогда
тогда  Углы COM и DCO равны как накрест лежащие при пересечении параллельных прямых OM и DC секущей OC. Луч OM — биссектриса угла EOC, поэтому
Углы COM и DCO равны как накрест лежащие при пересечении параллельных прямых OM и DC секущей OC. Луч OM — биссектриса угла EOC, поэтому  Находим:
Находим: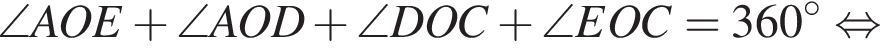




















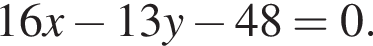 Из первого уравнения найдем
Из первого уравнения найдем  и подставим во второе. Получим:
и подставим во второе. Получим:  откуда
откуда 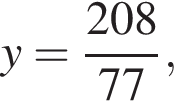
 Тогда
Тогда 


 поэтому
поэтому 

 и прямые параллельны.
и прямые параллельны. Значит, треугольник CHA равнобедренный прямоугольный, 3x = 9, x = 3. По теореме Пифагора получаем
Значит, треугольник CHA равнобедренный прямоугольный, 3x = 9, x = 3. По теореме Пифагора получаем  Тогда радиус окружности
Тогда радиус окружности  а
а 

 откуда
откуда  Значит,
Значит,  и
и 
 тогда
тогда 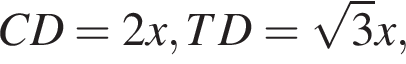

 поэтому треугольники KAD и KBC подобны с коэффициентом
поэтому треугольники KAD и KBC подобны с коэффициентом 






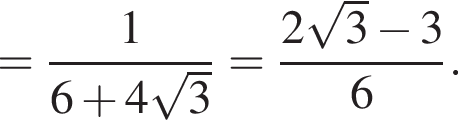



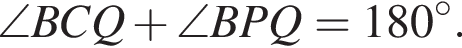 Отрезок MN — средняя линия трапеции ABCD, она параллельна основанию BC, а тогда
Отрезок MN — средняя линия трапеции ABCD, она параллельна основанию BC, а тогда  как односторонние углы при пересечении параллельных прямых секущей. Следовательно,
как односторонние углы при пересечении параллельных прямых секущей. Следовательно,  Для смежных углов справедливо равенство
Для смежных углов справедливо равенство  а потому
а потому 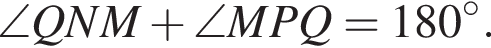 В четырёхугольнике MPQN сумма противоположных углов равна 180°, поэтому вокруг него можно описать окружность. Тем самым, точки M, N, P и Q лежат на одной окружности, что и требовалось доказать.
В четырёхугольнике MPQN сумма противоположных углов равна 180°, поэтому вокруг него можно описать окружность. Тем самым, точки M, N, P и Q лежат на одной окружности, что и требовалось доказать.  как соответственные углы при пересечении параллельных прямых секущей. В пункте а) было показано, что
как соответственные углы при пересечении параллельных прямых секущей. В пункте а) было показано, что  это означает, что
это означает, что  и, следовательно, точки A, D, P и Q также лежат на одной окружности.
и, следовательно, точки A, D, P и Q также лежат на одной окружности.  и
и 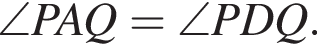 Значит, треугольники DPC и AQB подобны по двум углам. Следовательно,
Значит, треугольники DPC и AQB подобны по двум углам. Следовательно,  поскольку по условию отрезки DP и PC перпендикулярны.
поскольку по условию отрезки DP и PC перпендикулярны. 

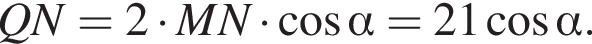 Осталось найти косинус угла CDA. Для этого на отрезке AD отметим точку E такую, что
Осталось найти косинус угла CDA. Для этого на отрезке AD отметим точку E такую, что  Тогда
Тогда 
 Для треугольника CDE запишем теорему косинусов:
Для треугольника CDE запишем теорему косинусов:






 Отсюда найдем
Отсюда найдем

 по теореме синусов для треугольника MPN можем найти радиус окружности, описанной около четырехугольника MPQN:
по теореме синусов для треугольника MPN можем найти радиус окружности, описанной около четырехугольника MPQN:
 найдем MQ по теореме синусов для треугольника MQN:
найдем MQ по теореме синусов для треугольника MQN:









 Пусть
Пусть  тогда
тогда  а
а  По свойству вписанного в окружность четырехугольника,
По свойству вписанного в окружность четырехугольника,  Угол PQN является смежным с ним, значит,
Угол PQN является смежным с ним, значит,  Поскольку сумма углов PMN и PQN равна 180°, около четырехугольника PQNM можно описать окружность.
Поскольку сумма углов PMN и PQN равна 180°, около четырехугольника PQNM можно описать окружность.
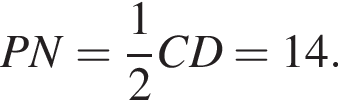





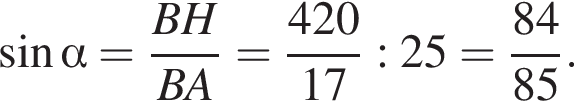


 причем AD = 2BC. Расстояние от точки D до прямой AB равно 10. Найдите расстояние от точки K до стороны AB.
причем AD = 2BC. Расстояние от точки D до прямой AB равно 10. Найдите расстояние от точки K до стороны AB. Следовательно,
Следовательно,


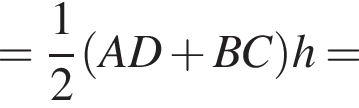

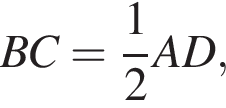 поэтому отрезок BC является средней линией треугольника AED. Заметим, что
поэтому отрезок BC является средней линией треугольника AED. Заметим, что  откуда
откуда 
 Таким образом, точка K лежит на средней линии трапеции. Тогда K — середина CD. Из подобия прямоугольных треугольников DH1E и KH2E, где DH1 и KH2 — перпендикуляры к AB, имеем:
Таким образом, точка K лежит на средней линии трапеции. Тогда K — середина CD. Из подобия прямоугольных треугольников DH1E и KH2E, где DH1 и KH2 — перпендикуляры к AB, имеем: 



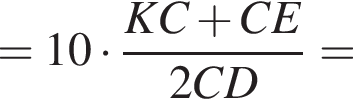


 Треугольники BLC и BEP подобны, следовательно,
Треугольники BLC и BEP подобны, следовательно, 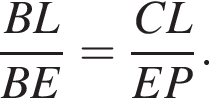 Таким образом,
Таким образом,  тогда
тогда  следовательно, отрезок EL является медианой треугольника CEK.
следовательно, отрезок EL является медианой треугольника CEK. откуда
откуда 
 тогда
тогда 
 а значит,
а значит,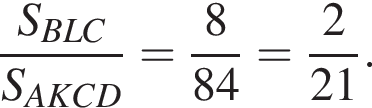
 и
и  Утроенный квадрат отношения расстояния от точки А до прямой CD к расстоянию от точки С до прямой AD равен 2, СD = 20.
Утроенный квадрат отношения расстояния от точки А до прямой CD к расстоянию от точки С до прямой AD равен 2, СD = 20. Пусть AH — высота треугольника ADC. Тогда
Пусть AH — высота треугольника ADC. Тогда 










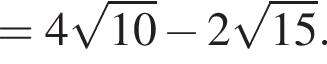



 следовательно, треугольники BMN и NKA подобны по соотношению двух сторон и равенству углов, заключенных между этими сторонами. Тогда
следовательно, треугольники BMN и NKA подобны по соотношению двух сторон и равенству углов, заключенных между этими сторонами. Тогда  следовательно, прямая BM параллельна прямой AN.
следовательно, прямая BM параллельна прямой AN. и
и  Из точек
Из точек 
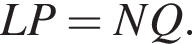 Тогда
Тогда  Следовательно,
Следовательно,


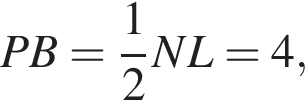
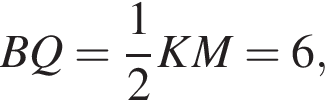



 поэтому
поэтому  Отсюда, по теореме косинусов, диагонали четырехугольника PBQC равны
Отсюда, по теореме косинусов, диагонали четырехугольника PBQC равны 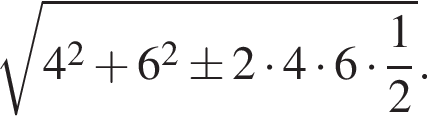 Без ограничения общности можно считать, что
Без ограничения общности можно считать, что 
 Далее, по формуле площади четырехугольника
Далее, по формуле площади четырехугольника


 угол CMD равен
угол CMD равен 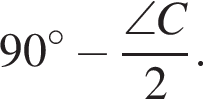 Поэтому угол
Поэтому угол  Но одновременно с этим он прямой. Таким образом,
Но одновременно с этим он прямой. Таким образом,  и прямые AB и CD параллельны.
и прямые AB и CD параллельны.


 тогда
тогда  Углы CDN и ADM равны как вертикальные, тогда
Углы CDN и ADM равны как вертикальные, тогда 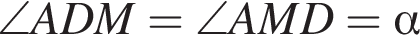 и
и  Тогда
Тогда  Таким образом, треугольники ABM и BCN равны по двум сторонам и углу между ними, следовательно, BM = BN.
Таким образом, треугольники ABM и BCN равны по двум сторонам и углу между ними, следовательно, BM = BN. Треугольник ACM также вписан в окружность, поэтому
Треугольник ACM также вписан в окружность, поэтому  Таким образом,
Таким образом, 






 Имеем:
Имеем:









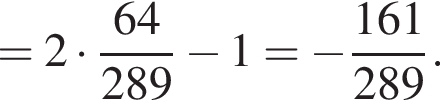
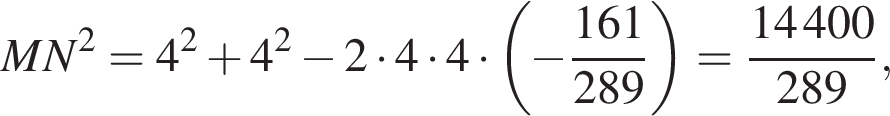









 Значит,
Значит,  поэтому
поэтому  следовательно,
следовательно, 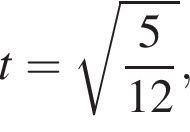 а
а 
 и
и  Но углы PCN и NAQ равны из параллельности прямых BС и AD. Значит, равны и углы PRN и NSQ, а значит, прямые PR параллельны SQ. Заметим, что точка N отлична от середины диагонали, следовательно, NP не равно NQ. Следовательно, в четырехугольнике SPRQ две стороны параллельны, но при этом он не является параллелограммом, поскольку его диагонали не делятся точкой пересечения пополам, значит, он является трапецией. Что и требовалось доказать.
Но углы PCN и NAQ равны из параллельности прямых BС и AD. Значит, равны и углы PRN и NSQ, а значит, прямые PR параллельны SQ. Заметим, что точка N отлична от середины диагонали, следовательно, NP не равно NQ. Следовательно, в четырехугольнике SPRQ две стороны параллельны, но при этом он не является параллелограммом, поскольку его диагонали не делятся точкой пересечения пополам, значит, он является трапецией. Что и требовалось доказать. Площадь трапеции равна
Площадь трапеции равна 


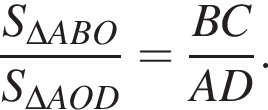


 Аналогично
Аналогично  поэтому
поэтому  Далее,
Далее,
 Окончательно получаем, что
Окончательно получаем, что 

 Отсюда
Отсюда 
 Таким образом, высота трапеции равна
Таким образом, высота трапеции равна 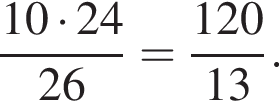
 AK = 3EL.
AK = 3EL. А угол EOA такой же. Что и требовалось доказать.
А угол EOA такой же. Что и требовалось доказать.
 Отсюда треугольники EMA и KML подобны по двум сторонам и углу между ними, причем коэффициент подобия равен 2. Заметим еще, что MO — диаметр окружности, описанной около треугольника KML. Поэтому, из теоремы синусов,
Отсюда треугольники EMA и KML подобны по двум сторонам и углу между ними, причем коэффициент подобия равен 2. Заметим еще, что MO — диаметр окружности, описанной около треугольника KML. Поэтому, из теоремы синусов, 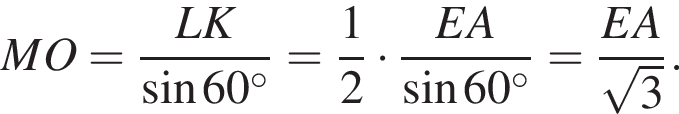







 Из предыдущего получаем что
Из предыдущего получаем что 

 Значит, угол AHB тоже равен 90°. Поэтому угол четырехугольника с вершиной H — прямой. Аналогично остальные углы этого четырехугольника прямые. Что и требовалось доказать.
Значит, угол AHB тоже равен 90°. Поэтому угол четырехугольника с вершиной H — прямой. Аналогично остальные углы этого четырехугольника прямые. Что и требовалось доказать.  Тогда и вторая диагональ прямоугольника равна a − b. Прямые GH и EF параллельны сторонам ABCD, поэтому угол между ними равен α. Тогда площадь прямоугольника равна
Тогда и вторая диагональ прямоугольника равна a − b. Прямые GH и EF параллельны сторонам ABCD, поэтому угол между ними равен α. Тогда площадь прямоугольника равна  Из условия получаем равенство:
Из условия получаем равенство:  Упрощая, получаем равенство
Упрощая, получаем равенство 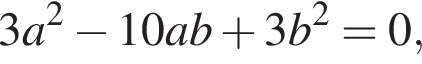 откуда a = 3b.
откуда a = 3b.

 и площадь трапеции FCDE равна
и площадь трапеции FCDE равна 
 и
и 







 угол D равен β, тогда
угол D равен β, тогда 
 следовательно,
следовательно, 
 Пусть EH — высота трапеции CFED, тогда
Пусть EH — высота трапеции CFED, тогда 

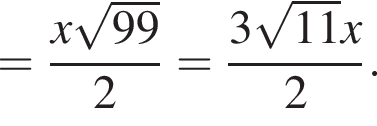

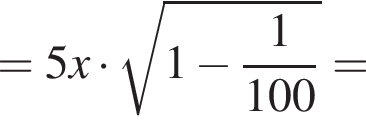


 следовательно,
следовательно,  Аналогичным способом вычислим длину BC:
Аналогичным способом вычислим длину BC: 





 Треугольник ABM равнобедренный, поэтому углы BAM и BMA равны
Треугольник ABM равнобедренный, поэтому углы BAM и BMA равны  Что и требовалось доказать.
Что и требовалось доказать. 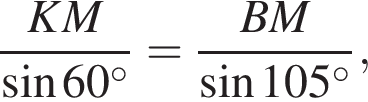 то есть
то есть  Угол KMN равен
Угол KMN равен  Применим теперь теорему косинусов для треугольника DMN:
Применим теперь теорему косинусов для треугольника DMN: 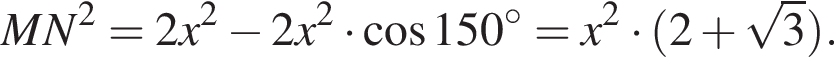











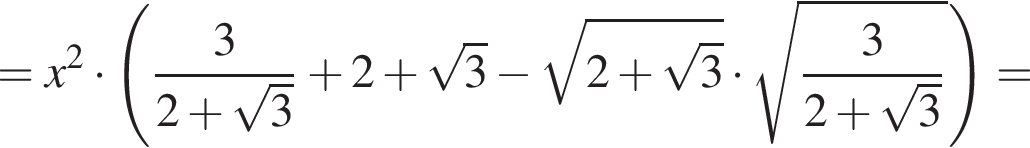












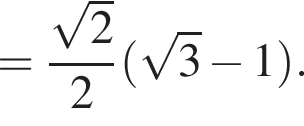






 получим KN = 37, откуда KN =
получим KN = 37, откуда KN = 



 Пусть площадь параллелограмма ABCD равна
Пусть площадь параллелограмма ABCD равна 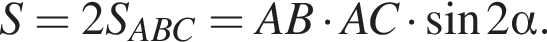 Треугольник ALD имеет общие с параллелограммом ABCD высоту и основание, следовательно,
Треугольник ALD имеет общие с параллелограммом ABCD высоту и основание, следовательно,  Таким образом,
Таким образом, 
 Таким образом, треугольник ALC равнобедренный,
Таким образом, треугольник ALC равнобедренный,  следовательно, EL проходит через точку O. Получаем:
следовательно, EL проходит через точку O. Получаем:



 и BO : AE = 1 : 2, что и требовалось доказать.
и BO : AE = 1 : 2, что и требовалось доказать.






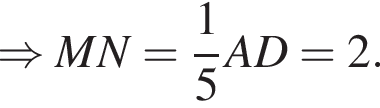


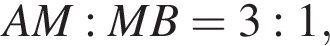
 и
и 
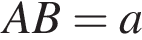 и
и  Тогда
Тогда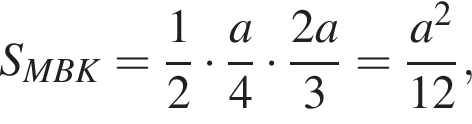











 и
и 






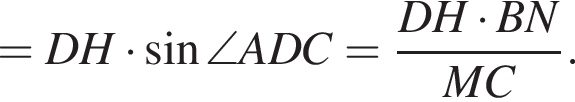


 Поскольку
Поскольку  получаем:
получаем: 
 Четырехугольник AMND вписан в окружность с диаметром MD, тогда
Четырехугольник AMND вписан в окружность с диаметром MD, тогда 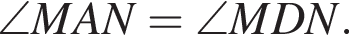 Следовательно, треугольники ABN и DCM подобны по двум углам, и отношение их высот равно отношению сторон, к которым эти высоты проведены.
Следовательно, треугольники ABN и DCM подобны по двум углам, и отношение их высот равно отношению сторон, к которым эти высоты проведены.
 что и требовалось доказать.
что и требовалось доказать.


 и
и 
 Основания KL и CD параллельны, поэтому
Основания KL и CD параллельны, поэтому








 тогда
тогда  и
и  Пусть отрезок LH — высота трапеции KCDL, следовательно,
Пусть отрезок LH — высота трапеции KCDL, следовательно, 
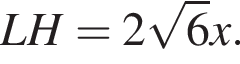 Тогда
Тогда 




 то есть
то есть 

 Тогда
Тогда 
 и
и  Находим основание BC:
Находим основание BC:





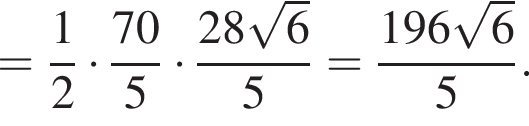

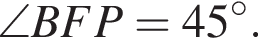

 откуда
откуда


 Далее,
Далее,  поэтому прямая FB есть биссектриса внешнего угла F треугольника QFC, а потому
поэтому прямая FB есть биссектриса внешнего угла F треугольника QFC, а потому 


 откуда находим:
откуда находим:

 поэтому
поэтому  Но вписанный угол, равный 135°, опирается на дугу в 270°, а потому точки B, F, D лежат на одной окружности с центром A, и тогда
Но вписанный угол, равный 135°, опирается на дугу в 270°, а потому точки B, F, D лежат на одной окружности с центром A, и тогда 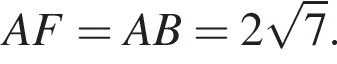 Таким образом,
Таким образом,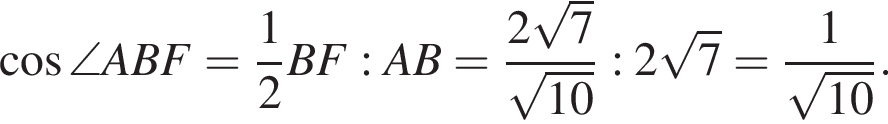


 Применяя обобщенную теорему синусов к треугольнику ABF, находим радиус описанной вокруг него окружности:
Применяя обобщенную теорему синусов к треугольнику ABF, находим радиус описанной вокруг него окружности:




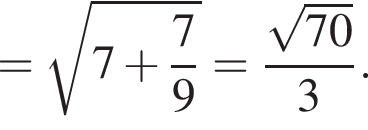
 откуда
откуда 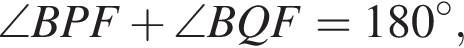 следовательно, вокруг четырехугольника BPFQ можно описать окружность, тогда углы BFP и BQP равны как углы, опирающиеся на одну дугу, поэтому
следовательно, вокруг четырехугольника BPFQ можно описать окружность, тогда углы BFP и BQP равны как углы, опирающиеся на одну дугу, поэтому 
 тогда
тогда  и вокруг четырехугольника APFD можно описать окружность. Следовательно, углы AFP и ADP равны как углы, опирающиеся на одну дугу. Пусть
и вокруг четырехугольника APFD можно описать окружность. Следовательно, углы AFP и ADP равны как углы, опирающиеся на одну дугу. Пусть  тогда из прямоугольного треугольника ADP
тогда из прямоугольного треугольника ADP 






 Аналогично, точки A, B, C, H лежат на окружности с диметром AC, значит,
Аналогично, точки A, B, C, H лежат на окружности с диметром AC, значит,  Отсюда
Отсюда  Таким образом, отрезки BH и ED параллельны по признаку параллельности.
Таким образом, отрезки BH и ED параллельны по признаку параллельности. По теореме синусов для окружности AECD получаем:
По теореме синусов для окружности AECD получаем:  Исключим АС, поделив одно равенство на другое, находим:
Исключим АС, поделив одно равенство на другое, находим:  откуда
откуда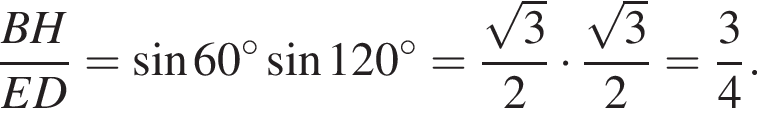





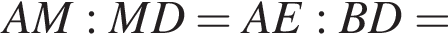

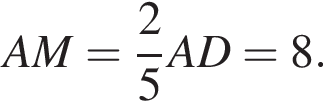 Аналогично ND = 8. Значит,
Аналогично ND = 8. Значит, 

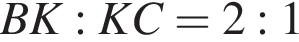 и
и 
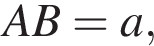 тогда
тогда










 Следовательно,
Следовательно,

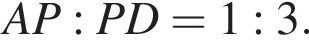 Через точку P проведена прямая, перпендикулярная стороне AD и пересекающая прямые CD и BC соответственно в точках
Через точку P проведена прямая, перпендикулярная стороне AD и пересекающая прямые CD и BC соответственно в точках  следовательно,
следовательно,  и
и  Значит, треугольник DPK равнобедренный. Находим:
Значит, треугольник DPK равнобедренный. Находим:
 Следовательно,
Следовательно, 
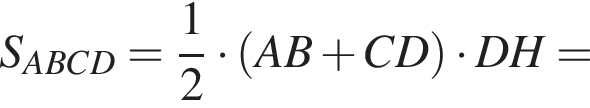


 а потому треугольник QCK равнобедренный. Следовательно,
а потому треугольник QCK равнобедренный. Следовательно,  откуда
откуда  Площадь треугольника QCK равна
Площадь треугольника QCK равна 




 точка O — точка пересечения AС и BD. Точка P — точка пересечения MN и AD, отрезок OH — высота треугольника AOD. Тогда
точка O — точка пересечения AС и BD. Точка P — точка пересечения MN и AD, отрезок OH — высота треугольника AOD. Тогда

 где
где  и
и  Треугольники AOH и ODH подобны, следовательно,
Треугольники AOH и ODH подобны, следовательно,  где
где  то есть
то есть  Находим:
Находим:






 Тогда
Тогда  откуда
откуда 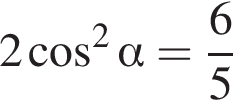 или
или  Заметим, что
Заметим, что 
 Получаем
Получаем  следовательно,
следовательно,  откуда
откуда 




 и
и 
 если известно, что
если известно, что  и
и 
 поэтому
поэтому  и
и  следовательно, треугольник AMO равнобедренный, а значит,
следовательно, треугольник AMO равнобедренный, а значит,  Тогда
Тогда  откуда следует, что отрезок MO параллелен стороне AD, поскольку накрест лежащие углы при секущей AO равны. Аналогично отрезок NO параллелен стороне BC. Следовательно, поскольку стороны BC и AD параллельны, точки М и N лежат на прямой, параллельной основаниям и проходящей через точку O. Что и требовалось доказать.
откуда следует, что отрезок MO параллелен стороне AD, поскольку накрест лежащие углы при секущей AO равны. Аналогично отрезок NO параллелен стороне BC. Следовательно, поскольку стороны BC и AD параллельны, точки М и N лежат на прямой, параллельной основаниям и проходящей через точку O. Что и требовалось доказать. тогда
тогда  и
и 
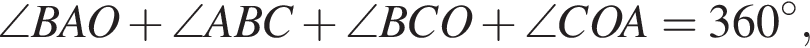




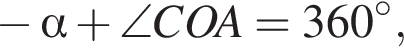
 Треугольник AOC равнобедренный, поэтому
Треугольник AOC равнобедренный, поэтому




 и
и  следовательно,
следовательно, 
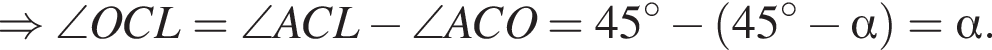
 значит,
значит, 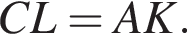
 Поэтому
Поэтому
 значит,
значит, 

 Тогда по теореме Пифагора в треугольнике CHD:
Тогда по теореме Пифагора в треугольнике CHD:
 Значит,
Значит, 
 при этом
при этом  следовательно,
следовательно, 




 В равнобедренном треугольнике AMO положим
В равнобедренном треугольнике AMO положим 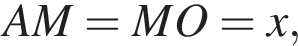 тогда
тогда  Далее, пусть
Далее, пусть  По свойству равнобедренной трапеции
По свойству равнобедренной трапеции  то есть
то есть  тогда в равнобедренном треугольнике CNO имеем:
тогда в равнобедренном треугольнике CNO имеем:


 то есть
то есть 

 В прямоугольном треугольнике AOP находим, что
В прямоугольном треугольнике AOP находим, что  Тогда треугольники AOP и COE равны по гипотенузе и острому углу. Откуда
Тогда треугольники AOP и COE равны по гипотенузе и острому углу. Откуда 
 и
и 



 получаем уравнение:
получаем уравнение:




 не подходит, поскольку угол α острый. Следовательно,
не подходит, поскольку угол α острый. Следовательно,  а потому искомое отношение равно 1 : 2.
а потому искомое отношение равно 1 : 2.




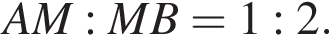





 Для треугольников AMO и CFO по теореме косинусов:
Для треугольников AMO и CFO по теореме косинусов: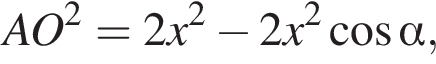

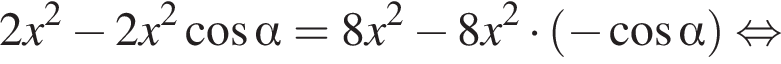



 Имеем:
Имеем: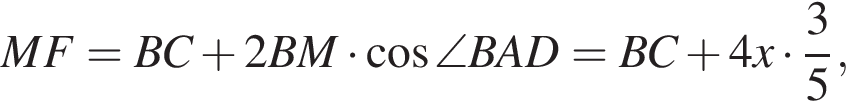



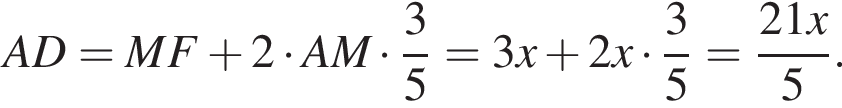

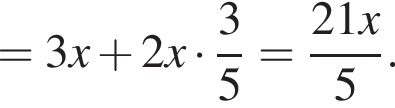
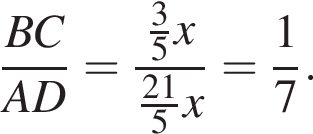
 Значит,
Значит, 

 тогда
тогда 



 Значит,
Значит,  Тогда из треугольника MOL:
Тогда из треугольника MOL:

 поэтому
поэтому  откуда
откуда  Тогда
Тогда


 и удалена от AD на R. Точка Q равноудалена от сторон AD и CD квадрата ABCD, значит, точка Q лежит на диагонали BD и делит её в отношении 1 : 2, считая от D. Аналогично точка P, диаметрально противоположная точке L, лежит на диагонали BD и делит её в отношении 1 : 2, считая от B. Следовательно,
и удалена от AD на R. Точка Q равноудалена от сторон AD и CD квадрата ABCD, значит, точка Q лежит на диагонали BD и делит её в отношении 1 : 2, считая от D. Аналогично точка P, диаметрально противоположная точке L, лежит на диагонали BD и делит её в отношении 1 : 2, считая от B. Следовательно, 
 Тогда
Тогда 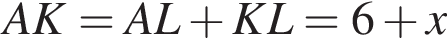 и
и
 то есть
то есть 
 Прямоугольные треугольники EDK и ECB подобны с коэффициентом
Прямоугольные треугольники EDK и ECB подобны с коэффициентом  следовательно,
следовательно, 
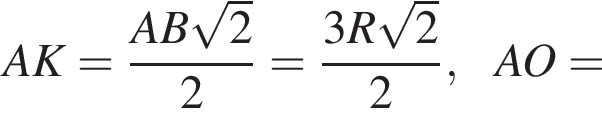













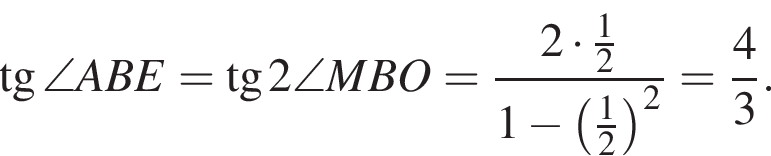
 откуда находим:
откуда находим:





 По теореме Пифагора в треугольнике ABD находим
По теореме Пифагора в треугольнике ABD находим  По свойству касательной и секущей получаем:
По свойству касательной и секущей получаем:  то есть
то есть 

 Решением этого уравнения является
Решением этого уравнения является 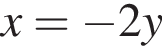 (не подходит) или
(не подходит) или  Находим:
Находим:




 следовательно,
следовательно,

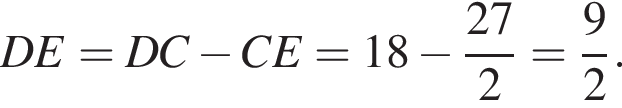

 Значит,
Значит,  поскольку треугольники KOF и NCF подобны, и
поскольку треугольники KOF и NCF подобны, и  поскольку треугольники KOQ и NDQ равны. Если
поскольку треугольники KOQ и NDQ равны. Если  то
то 
 и
и



 Кроме того,
Кроме того,  Тогда
Тогда
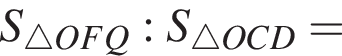



 а потому
а потому




 CN = AN = 24.
CN = AN = 24. 


 Следовательно,
Следовательно, 


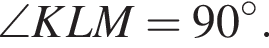 Аналогично все углы четырёхугольника KLMN прямые. Следовательно, это прямоугольник.
Аналогично все углы четырёхугольника KLMN прямые. Следовательно, это прямоугольник. 
 и
и 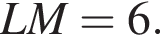 Заметим, что точки K и M лежат на средней линии трапеции PQ. Получаем
Заметим, что точки K и M лежат на средней линии трапеции PQ. Получаем  тогда
тогда  то есть
то есть  Находим:
Находим:

 где
где  Значит,
Значит,  и
и 



 Таким образом,
Таким образом, 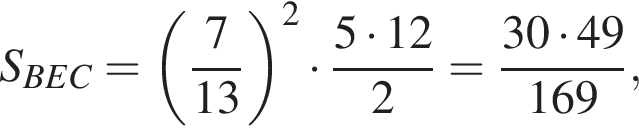





 и
и 




 Треугольники PCO и DEO подобны, причем
Треугольники PCO и DEO подобны, причем


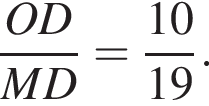
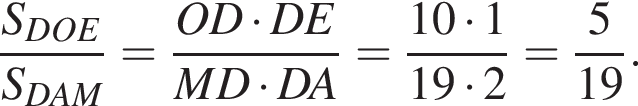



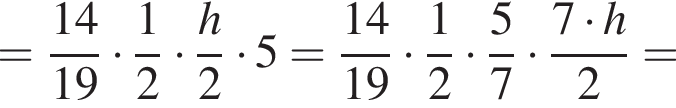









 Кроме того,
Кроме того, 
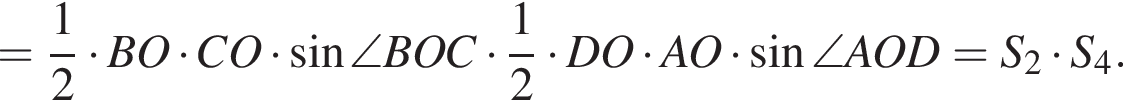




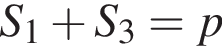 и
и  значит, S1 и S3 — корни уравнения
значит, S1 и S3 — корни уравнения  Корнями этого же уравнения являются S2 и S4, откуда следует, что
Корнями этого же уравнения являются S2 и S4, откуда следует, что  или
или  Из условия
Из условия  получаем
получаем  следовательно, отрезок AO является медианой треугольника ABD.
следовательно, отрезок AO является медианой треугольника ABD.
 тогда
тогда

 и
и  поэтому
поэтому

 и
и  Из подобия треугольников BEF и DEA получаем:
Из подобия треугольников BEF и DEA получаем:
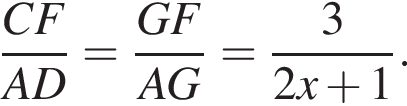
 значит,
значит, 





 Но из пункта а) следует, что CF = AD, поэтому
Но из пункта а) следует, что CF = AD, поэтому  значит,
значит,  Тогда треугольники
Тогда треугольники  поскольку треугольник ABD равен треугольнику BCD. Таким образом,
поскольку треугольник ABD равен треугольнику BCD. Таким образом,
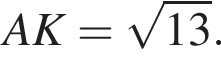

 значит,
значит,  по обратной теореме Пифагора. Тогда
по обратной теореме Пифагора. Тогда  Следовательно, треугольники ABE и ECK подобны по двум углам. Из подобия имеем:
Следовательно, треугольники ABE и ECK подобны по двум углам. Из подобия имеем:








 поскольку 13 = 9 + 4. Значит, треугольник AKE прямоугольный с прямым углом
поскольку 13 = 9 + 4. Значит, треугольник AKE прямоугольный с прямым углом 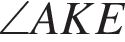 по теореме, обратной теореме Пифагора. Из рисунка видно, что
по теореме, обратной теореме Пифагора. Из рисунка видно, что  является внешним для прямоугольного треугольника ABK
является внешним для прямоугольного треугольника ABK  по определению квадрата), следовательно, он равен сумме двух несмежных с ним углов:
по определению квадрата), следовательно, он равен сумме двух несмежных с ним углов: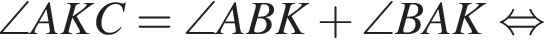




 откуда x = 3y. По теореме Пифагора для треугольника ABK получаем:
откуда x = 3y. По теореме Пифагора для треугольника ABK получаем:
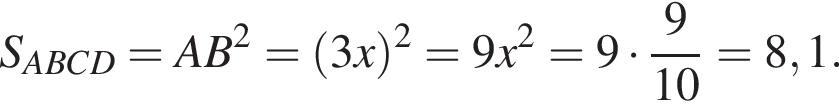

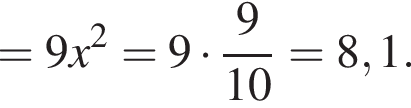
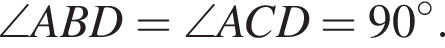


 то есть
то есть


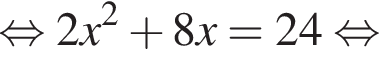

 пополам. Отрезок DN перпендикулярен отрезку AM и делит сторону AB в отношении AN : NB = 5 : 1.
пополам. Отрезок DN перпендикулярен отрезку AM и делит сторону AB в отношении AN : NB = 5 : 1.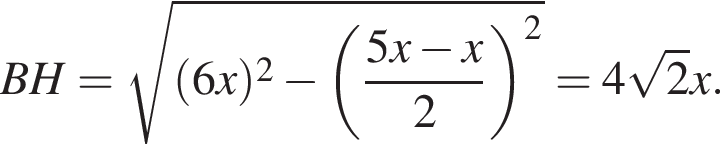
 откуда
откуда





 тогда
тогда  Кроме того,
Кроме того, 
 равен
равен  равны как накрест лежащие при пересечении параллельных прямых секущей, тогда равны и
равны как накрест лежащие при пересечении параллельных прямых секущей, тогда равны и  и
и  Следовательно, подобны треугольники ABK и PCK по трем углам, а потому треугольник PCK равнобедренный. Запишем пропорцию:
Следовательно, подобны треугольники ABK и PCK по трем углам, а потому треугольник PCK равнобедренный. Запишем пропорцию:









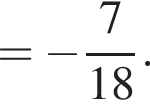




 Треугольники ABK и ADP подобны по трем углам, поэтому
Треугольники ABK и ADP подобны по трем углам, поэтому  откуда
откуда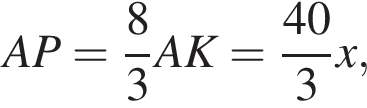


 тогда
тогда 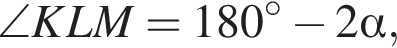
 как углы равнобокой трапеции при общем основании, значит,
как углы равнобокой трапеции при общем основании, значит,  (см. рис. 1). Треугольник BMO равнобедренный по признаку, откуда
(см. рис. 1). Треугольник BMO равнобедренный по признаку, откуда
 параллельны прямые AO и KN. Отрезки AO и BO параллельны одной и той же прямой, поэтому точки A, O и B лежат на одной прямой.
параллельны прямые AO и KN. Отрезки AO и BO параллельны одной и той же прямой, поэтому точки A, O и B лежат на одной прямой.




 Далее, из подобия пар треугольников PMO и KQO и MOB и MQN следует, что
Далее, из подобия пар треугольников PMO и KQO и MOB и MQN следует, что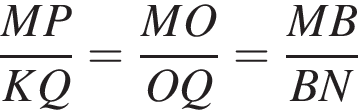


 то есть
то есть
 Из (1) и (3) получаем:
Из (1) и (3) получаем:









 Аналогично в треугольнике AOC отрезок PK — средняя линия, она параллельна стороне AC и
Аналогично в треугольнике AOC отрезок PK — средняя линия, она параллельна стороне AC и  Тогда отрезки MN и PK параллельны и равны, значит, четырехугольник MNKP — параллелограмм.
Тогда отрезки MN и PK параллельны и равны, значит, четырехугольник MNKP — параллелограмм.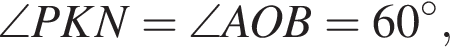

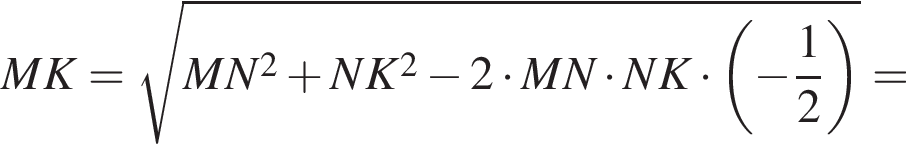
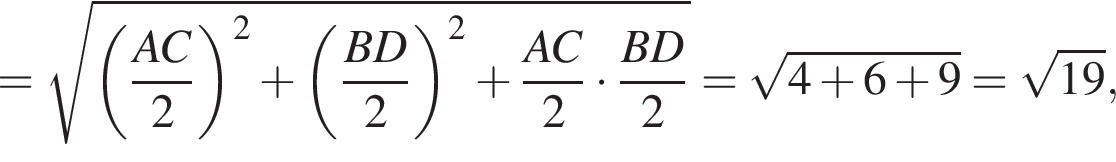

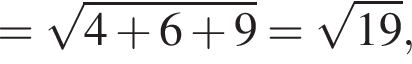

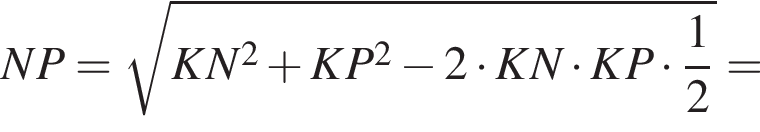
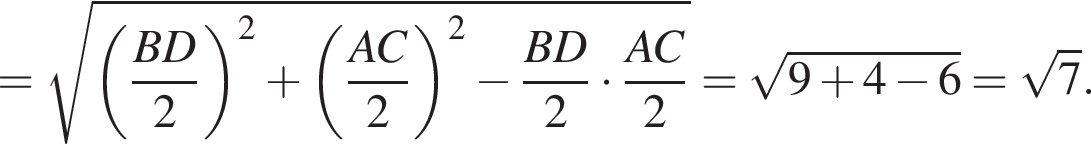





 Аналогично
Аналогично  Кроме того, KN = LM, то есть равны треугольники AKN и CLM. Отсюда AN = CL, тогда треугольники ANO и CLO равны по стороне и двум прилежащим к ней углам. Итак, AO = CO, LO = NO, значит, точка O является центром и ромба, и параллелограмма.
Кроме того, KN = LM, то есть равны треугольники AKN и CLM. Отсюда AN = CL, тогда треугольники ANO и CLO равны по стороне и двум прилежащим к ней углам. Итак, AO = CO, LO = NO, значит, точка O является центром и ромба, и параллелограмма.

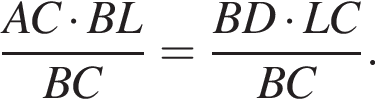
 Запишем отношения площадей:
Запишем отношения площадей:












 Следовательно,
Следовательно,  По теореме Менелая для треугольника BMD и секущей OK получим:
По теореме Менелая для треугольника BMD и секущей OK получим:



 Найдем площадь четырехугольника KODM:
Найдем площадь четырехугольника KODM:


 Тогда из подобия треугольников BEC и FED по двум углам получаем, что
Тогда из подобия треугольников BEC и FED по двум углам получаем, что  то есть
то есть  По теореме Менелая для треугольника ACD и секущей OE находим:
По теореме Менелая для треугольника ACD и секущей OE находим: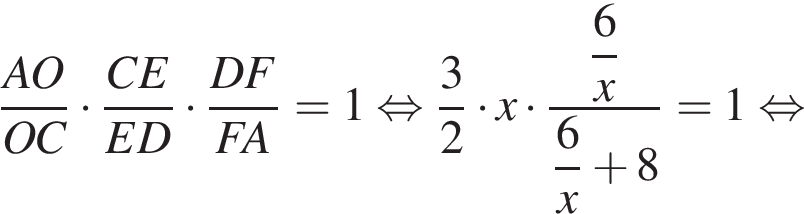
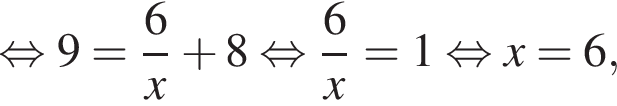


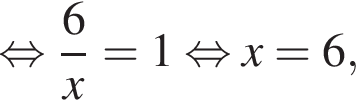

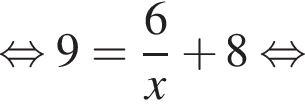

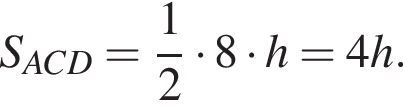




 В треугольниках ABE и EDF углы при основании равны, а потому
В треугольниках ABE и EDF углы при основании равны, а потому  Углы BCA и CAD равны как накрест лежащие при пересечении параллельных прямых секущей. Кроме того,
Углы BCA и CAD равны как накрест лежащие при пересечении параллельных прямых секущей. Кроме того,


 тогда
тогда 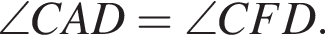 Следовательно, точки A, F, С и D лежат на одной окружности.
Следовательно, точки A, F, С и D лежат на одной окружности. и
и  В равнобедренной трапеции диагонали равны, то есть
В равнобедренной трапеции диагонали равны, то есть  Тогда искомое расстояние равно
Тогда искомое расстояние равно

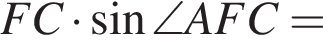


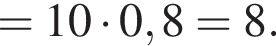
 Следовательно, треугольник AMO равнобедренный и
Следовательно, треугольник AMO равнобедренный и  Аналогично
Аналогично  Поскольку
Поскольку  получаем:
получаем: 
 Тогда
Тогда 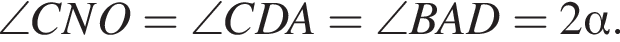
 Тогда
Тогда  По теореме косинусов для треугольников AMO и CNO имеем:
По теореме косинусов для треугольников AMO и CNO имеем: