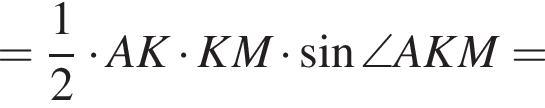Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй —
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны
Решение. а) Обозначим центры окружностей O1 и O2 соответственно. Пусть общая касательная, проведённая к окружностям в точке K, пересекает AB в точке M. По свойству касательных, проведённых из одной точки, AM = KM и KM = BM. Треугольник AKB, у которого медиана равна половине стороны, к которой она проведена, — прямоугольный. Вписанный угол AKD прямой, поэтому он опирается на диаметр AD. Значит, AD ⊥ AB. Аналогично получаем, что BC ⊥ AB. Следовательно, прямые AD и BC параллельны.
б) Пусть, для определенности, радиус окружности с центром в точке O1 равен 4, а радиус окружности с центром в точке O2 равен 1. Треугольники BKC и AKD подобны,  Пусть
Пусть  тогда
тогда  У треугольников AKD и AKB общая высота, следовательно,
У треугольников AKD и AKB общая высота, следовательно,

то есть SAKB = 4S. Аналогично, SCKD = 4S. Площадь трапеции ABCD равна 25S.
Вычислим площадь трапеции ABCD. Заметим, что  Проведём к AD перпендикуляр O2H, равный высоте трапеции, и найдём его из прямоугольного треугольника O2HO1. Получаем:
Проведём к AD перпендикуляр O2H, равный высоте трапеции, и найдём его из прямоугольного треугольника O2HO1. Получаем:


Следовательно, 25S = 20, откуда S = 0,8 и SAKB = 4S = 3,2.
Ответ: б) 3,2.
Приведем решение пункта б) Рамиля Багавиева.
Вычислим площадь трапеции ABCD. Заметим, что  Проведём к AD перпендикуляр O2H, равный высоте трапеции, и найдём его из прямоугольного треугольника O2HO1:
Проведём к AD перпендикуляр O2H, равный высоте трапеции, и найдём его из прямоугольного треугольника O2HO1:

Из подобия треугольников AKD и AKB следует  таким образом, AK = 2BK. Применим теорему Пифагора к треугольнику AKB, находим:
таким образом, AK = 2BK. Применим теорему Пифагора к треугольнику AKB, находим:



Тогда 
 откуда получаем:
откуда получаем:

| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) ИЛИ имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) ИЛИ при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | 1 |
| Решение не соответствует ни одному из критериев, приведённых выше | 0 |
| Максимальный балл | 3 |











 Из этого уравнения находим, что
Из этого уравнения находим, что 


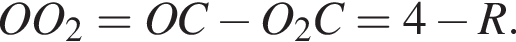







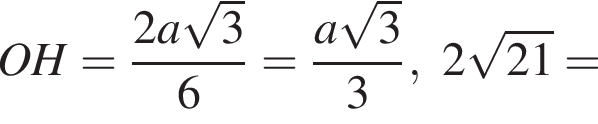



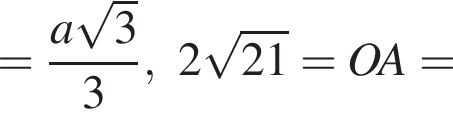




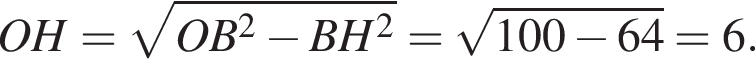









 и
и  поскольку угол между касательной и хордой равен половине заключённой между ними дуги. Тогда
поскольку угол между касательной и хордой равен половине заключённой между ними дуги. Тогда  равны Соответственные углы при пересечении прямых KM и BC равны, поэтому данные прямые параллельны.
равны Соответственные углы при пересечении прямых KM и BC равны, поэтому данные прямые параллельны. по теореме Фалеса. Осталось найти AР.
по теореме Фалеса. Осталось найти AР. то есть
то есть  Следовательно,
Следовательно, 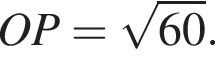 По теореме Пифагора
По теореме Пифагора  Окончательно получаем:
Окончательно получаем: 























 поэтому четырехугольник AECD — вписанная трапеция, следовательно, углы ADC и EAD равны, также
поэтому четырехугольник AECD — вписанная трапеция, следовательно, углы ADC и EAD равны, также  из параллельности. Таким образом,
из параллельности. Таким образом,  и
и  следовательно, треугольники ACD и ABE подобны по двум углам. Что требовалось доказать.
следовательно, треугольники ACD и ABE подобны по двум углам. Что требовалось доказать. а значит, BA — касательная к окружности AECD. Тогда
а значит, BA — касательная к окружности AECD. Тогда 

 (опираются на диаметры), следовательно, четырехугольник CEDB — прямоугольная трапеция
(опираются на диаметры), следовательно, четырехугольник CEDB — прямоугольная трапеция  что требовалось доказать.
что требовалось доказать.











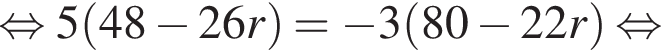


 треугольник равнобедренный, следовательно, отрезок AN является также медианой этого треугольника, а значит,
треугольник равнобедренный, следовательно, отрезок AN является также медианой этого треугольника, а значит,  Что требовалось доказать.
Что требовалось доказать.  Пусть DN пересекает вторую окружность в точке C1. Из симметрии заключаем, что
Пусть DN пересекает вторую окружность в точке C1. Из симметрии заключаем, что  следовательно,
следовательно,  (последнее равенство вытекает из свойств вписанных углов). Тогда треугольники CMN и MDN подобны, значит,
(последнее равенство вытекает из свойств вписанных углов). Тогда треугольники CMN и MDN подобны, значит, 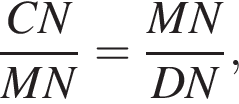 то есть
то есть  откуда MN = 9.
откуда MN = 9. Прямая AB — диаметр окружности меньшего радиуса. По теореме косинусов
Прямая AB — диаметр окружности меньшего радиуса. По теореме косинусов

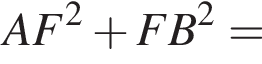


 откуда
откуда






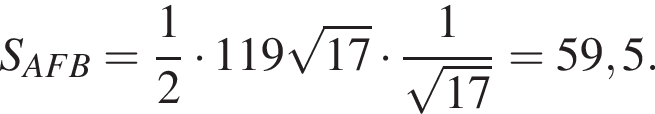
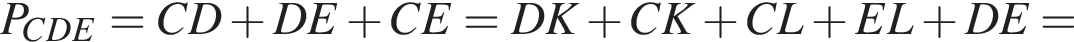










 Получаем, что
Получаем, что



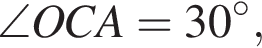 поэтому
поэтому  Аналогично
Аналогично  откуда
откуда 
 что и требовалось доказать.
что и требовалось доказать. По теореме косинусов в треугольнике KOO1 имеем:
По теореме косинусов в треугольнике KOO1 имеем:

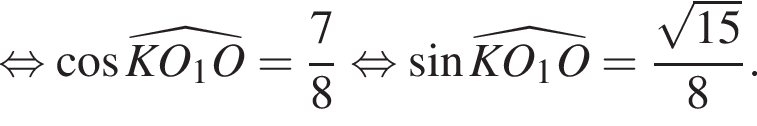
 Поскольку MOT прямоугольный, то OM — высота и медиана в треугольнике KO1T. Таким образом, KT = 2KM =
Поскольку MOT прямоугольный, то OM — высота и медиана в треугольнике KO1T. Таким образом, KT = 2KM = 
 Общая хорда перпендикулярна линии центров и делится этой линией пополам, поэтому
Общая хорда перпендикулярна линии центров и делится этой линией пополам, поэтому 
 радиус второй окружности втрое больше радиуса первой и AB = 3.
радиус второй окружности втрое больше радиуса первой и AB = 3. так как линия центров
так как линия центров 
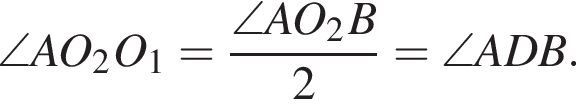
 подобны по двум углам.
подобны по двум углам. следует параллельность прямых:
следует параллельность прямых: 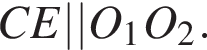 Учитывая, что
Учитывая, что  Значит,
Значит,  а AE — диаметр окружности. По условию
а AE — диаметр окружности. По условию 




 откуда
откуда 
 В треугольнике DAO2 известны стороны:
В треугольнике DAO2 известны стороны:  По теореме косинусов находим:
По теореме косинусов находим:

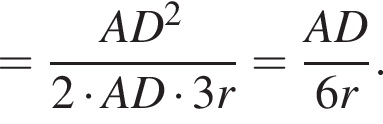


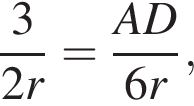 откуда
откуда 
 Прямые PC и AQ пересекаются в точке K. Найдите отношение
Прямые PC и AQ пересекаются в точке K. Найдите отношение 

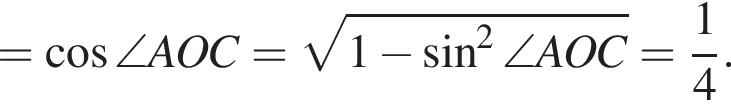


 центральный, а
центральный, а  — вписанный угол. Аналогично
— вписанный угол. Аналогично 
 и
и  поэтому по двум равным углам
поэтому по двум равным углам  и
и  подобны, что и требовалось доказать.
подобны, что и требовалось доказать. верно, поскольку
верно, поскольку  тогда по теореме, обратной теореме Пифагора,
тогда по теореме, обратной теореме Пифагора,  прямоугольный,
прямоугольный,  Найдем высоту
Найдем высоту  проведенную из
проведенную из 
 поэтому коэффициент подобия равен
поэтому коэффициент подобия равен  Расстояние от точки B до прямой MK, равное высоте
Расстояние от точки B до прямой MK, равное высоте  проведенной из вершины
проведенной из вершины 
 то есть медиана CM треугольника ABC равна половине стороны AB. Значит,
то есть медиана CM треугольника ABC равна половине стороны AB. Значит,  Тогда
Тогда  поэтому AE — диаметр меньшей окружности. Следовательно, прямая AE перпендикулярна прямой AB. Аналогично докажем, что прямая BD перпендикулярна прямой AB. Прямые AE и BD перпендикулярны одной и той же прямой AB, значит, они параллельны.
поэтому AE — диаметр меньшей окружности. Следовательно, прямая AE перпендикулярна прямой AB. Аналогично докажем, что прямая BD перпендикулярна прямой AB. Прямые AE и BD перпендикулярны одной и той же прямой AB, значит, они параллельны. Проведем равный AB перпендикуляр EF из точки E на BD. Тогда:
Проведем равный AB перпендикуляр EF из точки E на BD. Тогда:


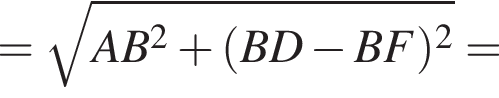












 По теореме Пифагора находим:
По теореме Пифагора находим: 

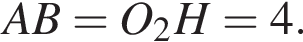 Из прямоугольного треугольника BAD получаем:
Из прямоугольного треугольника BAD получаем: 
 поэтому
поэтому 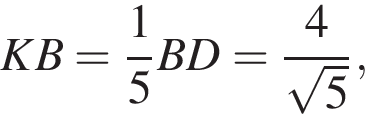 а
а 
 тогда
тогда 




 Отношение площадей кругов равно
Отношение площадей кругов равно  Подставим CH в формулу тангенса четвёртой степени:
Подставим CH в формулу тангенса четвёртой степени:
 поэтому CPHQ — прямоугольник. Заметим, что площадь искомого четырёхугольника состоит из суммы площадей треугольников HPO1, PHQ и HQO2. Более того, площади этих фигур являются половинами площадей APH, PHQC и HQB соответственно. Таким образом,
поэтому CPHQ — прямоугольник. Заметим, что площадь искомого четырёхугольника состоит из суммы площадей треугольников HPO1, PHQ и HQO2. Более того, площади этих фигур являются половинами площадей APH, PHQC и HQB соответственно. Таким образом, 

 Пусть AC = BC = x, заметим, что CE : CB = 15 : 8, следовательно,
Пусть AC = BC = x, заметим, что CE : CB = 15 : 8, следовательно, 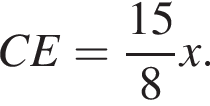 По теореме Пифагора для треугольника ACE
По теореме Пифагора для треугольника ACE
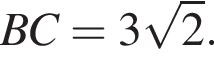 Прямая AC вторично пересекает окружность в точке D. Точка E диаметрально противоположна точке D. Прямые ED и BC пересекаются в точке F.
Прямая AC вторично пересекает окружность в точке D. Точка E диаметрально противоположна точке D. Прямые ED и BC пересекаются в точке F.
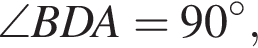 поскольку этот угол опирается на диаметр AB. Тогда BD — высота прямоугольного треугольника ABC. По свойству высоты получаем, что
поскольку этот угол опирается на диаметр AB. Тогда BD — высота прямоугольного треугольника ABC. По свойству высоты получаем, что  тогда
тогда  Треугольники EOB и DOA равны по двум сторонам и углу между ними, значит, EB = AD, откуда
Треугольники EOB и DOA равны по двум сторонам и углу между ними, значит, EB = AD, откуда 














 Таким образом, C — середина BF и
Таким образом, C — середина BF и  Следовательно,
Следовательно,


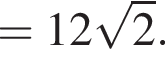






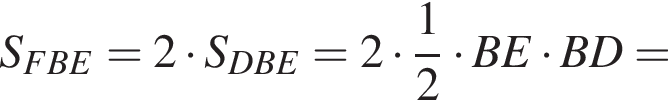



 Аналогично
Аналогично 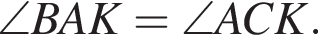 Таким образом,
Таким образом, 





 значит,
значит, 
 Из подобия треугольников AKC и AKB получаем, что
Из подобия треугольников AKC и AKB получаем, что  Отсюда
Отсюда  и коэффициент подобия равен 2.
и коэффициент подобия равен 2.  Значит,
Значит, 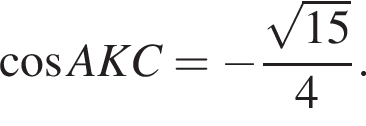 Запишем теорему косинусов для треугольника AKC:
Запишем теорему косинусов для треугольника AKC: 

 тогда
тогда  откуда находим площадь треугольника ABC:
откуда находим площадь треугольника ABC: 




 то есть
то есть  откуда
откуда




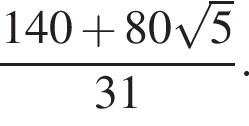

 значит,
значит, 


 следовательно, дуга
следовательно, дуга  тогда
тогда  Далее, из симметрии относительно CC1 следует, что
Далее, из симметрии относительно CC1 следует, что  Тогда для равных дуг получаем:
Тогда для равных дуг получаем:
 тогда
тогда









 BC = 5.
BC = 5.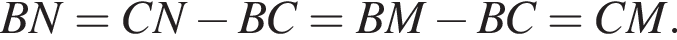 Что и требовалось доказать.
Что и требовалось доказать. поэтому угол BAC прямой. Тогда треугольники O2IA и O1KA равнобедренные прямоугольные. Отсюда
поэтому угол BAC прямой. Тогда треугольники O2IA и O1KA равнобедренные прямоугольные. Отсюда 


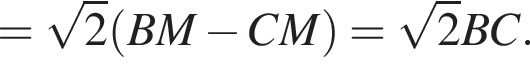












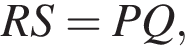










 a AB = 6, расположены две окружности. Окружность с центром в точке K, радиус которой равен 2, касается сторон AB и АD. Окружность с центром в точке L, радиус которой равен 1, касается стороны CD и первой окружности.
a AB = 6, расположены две окружности. Окружность с центром в точке K, радиус которой равен 2, касается сторон AB и АD. Окружность с центром в точке L, радиус которой равен 1, касается стороны CD и первой окружности.  KL = 3, LN = 1. По теореме Пифагора из прямоугольной трапеции PKLN получим:
KL = 3, LN = 1. По теореме Пифагора из прямоугольной трапеции PKLN получим: 
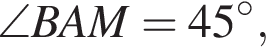 поэтому BAM равнобедренный прямоугольный треугольник,
поэтому BAM равнобедренный прямоугольный треугольник, 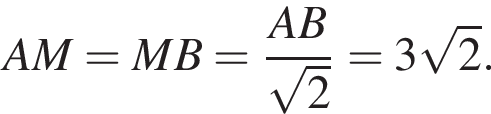
 поэтому
поэтому  Пусть T — проекция точки C на прямую BM. Тогда высота треугольника CLM, проведенная к ML, равна TM. Заметим, что
Пусть T — проекция точки C на прямую BM. Тогда высота треугольника CLM, проведенная к ML, равна TM. Заметим, что 
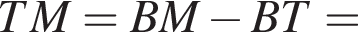




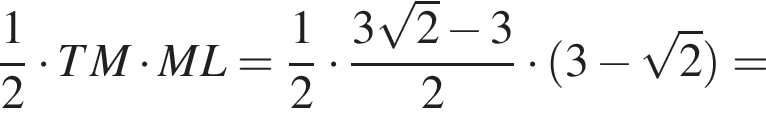




 и
и 




 У прямоугольных треугольников CND и CHB общий острый угол при вершине C, поэтому
У прямоугольных треугольников CND и CHB общий острый угол при вершине C, поэтому  Треугольник ABC подобен треугольнику NMC по двум углам, значит,
Треугольник ABC подобен треугольнику NMC по двум углам, значит, 
 следовательно,
следовательно, 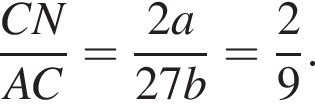

 и
и  Тогда по теореме о внешнем угле
Тогда по теореме о внешнем угле  и
и  значит,
значит,  следовательно, четырехугольник CDNM вписан в окружность.
следовательно, четырехугольник CDNM вписан в окружность.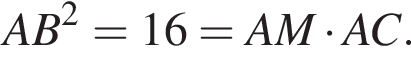 Запишем степень точки A относительно окружности, описанной около CMD:
Запишем степень точки A относительно окружности, описанной около CMD:  то есть
то есть 

 Отсюда
Отсюда 



 вписанный. Что и требовалось доказать.
вписанный. Что и требовалось доказать. p = 18, отсюда
p = 18, отсюда  Значит, радиус окружности, вписанной в DFG равен
Значит, радиус окружности, вписанной в DFG равен 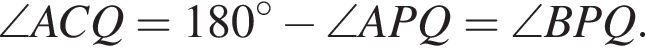







 Заметим, что отрезок MN — проекция отрезка O1O2 на прямую AB, следовательно,
Заметим, что отрезок MN — проекция отрезка O1O2 на прямую AB, следовательно,  откуда
откуда  Аналогично
Аналогично  Значит,
Значит,  Равенство достигается в случае, когда прямые AB и PQ взаимно перпендикулярны и прямые CD и PQ взаимно перпендикулярны.
Равенство достигается в случае, когда прямые AB и PQ взаимно перпендикулярны и прямые CD и PQ взаимно перпендикулярны.


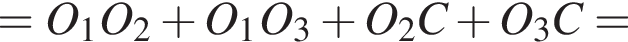


 Отрезки O3D и O1O2 взаимно перпендикулярны, поскольку проведенный в точку касания радиус перпендикулярен касательной. Тогда
Отрезки O3D и O1O2 взаимно перпендикулярны, поскольку проведенный в точку касания радиус перпендикулярен касательной. Тогда







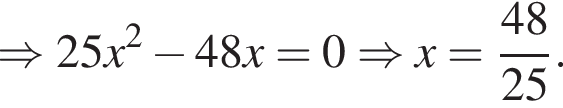









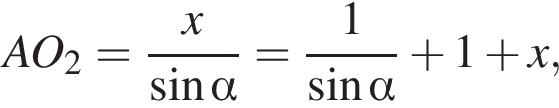
 Далее,
Далее, 
 то есть
то есть



 откуда получаем, что x = 2 и y = 4, то есть
откуда получаем, что x = 2 и y = 4, то есть  следовательно, сумма длин второй и третьей окружностей составит
следовательно, сумма длин второй и третьей окружностей составит 

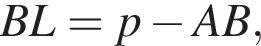 где p — полупериметр треугольника ABC.
где p — полупериметр треугольника ABC.  или
или  Но тогда
Но тогда  что и требовалось доказать.
что и требовалось доказать. тогда угол ACB равен 90°, из чего следует, что четырехугольник CLO1M — квадрат. Таким образом,
тогда угол ACB равен 90°, из чего следует, что четырехугольник CLO1M — квадрат. Таким образом, 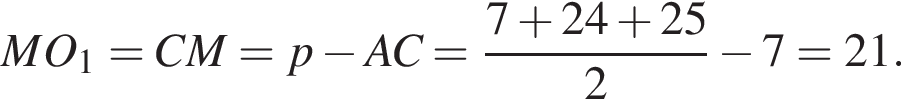

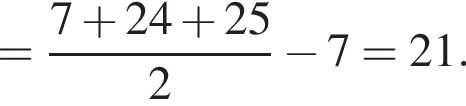

 Тогда по тереме Пифагора
Тогда по тереме Пифагора









 Значит,
Значит,  Далее, вновь используя свойство биссектрисы, получаем, что
Далее, вновь используя свойство биссектрисы, получаем, что 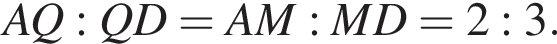


 По теореме Пифагора:
По теореме Пифагора: 






 откуда AC = 13, а тогда AO = EO = 6,5.
откуда AC = 13, а тогда AO = EO = 6,5.
 тогда
тогда


 Тогда четырехугольник O1KO2L вписан в окружность. Значит, углы
Тогда четырехугольник O1KO2L вписан в окружность. Значит, углы  равны как вписанные, опирающиеся на одну и ту же дугу.
равны как вписанные, опирающиеся на одну и ту же дугу.  и
и  Следовательно,
Следовательно, 

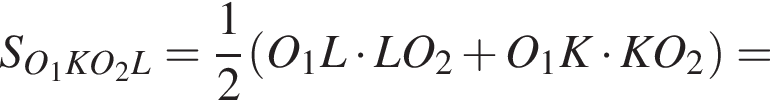





 откуда
откуда  то есть x = 3.
то есть x = 3. как вертикальные и
как вертикальные и 
 Что и требовалось доказать.
Что и требовалось доказать. Из пункта а) следует, что
Из пункта а) следует, что 
 откуда
откуда  Следовательно,
Следовательно, 


 Отсюда треугольники APB и BPM подобны, то есть
Отсюда треугольники APB и BPM подобны, то есть  следовательно,
следовательно, 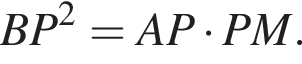 Аналогично треугольники APC и CPM подобны, откуда
Аналогично треугольники APC и CPM подобны, откуда  следовательно,
следовательно,  Значит, BP = CP. Что и требовалось доказать.
Значит, BP = CP. Что и требовалось доказать.

 следовательно, углы MCB и MBC в сумме составляют острый угол, значит, каждый из них меньше 90°. Тогда
следовательно, углы MCB и MBC в сумме составляют острый угол, значит, каждый из них меньше 90°. Тогда

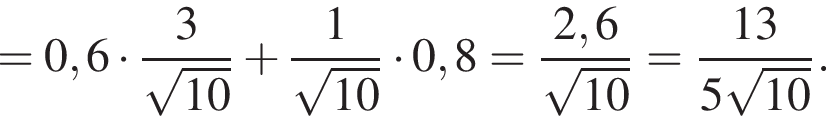

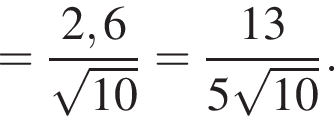




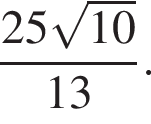

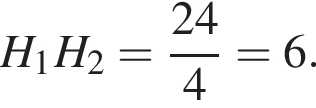 Находим:
Находим: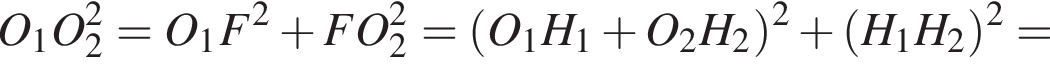
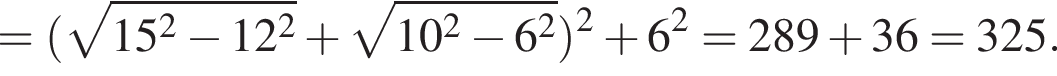


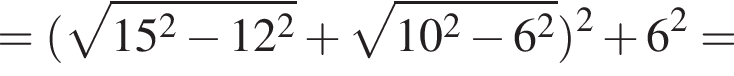
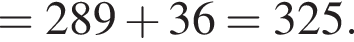

 С центром в точке О построена окружность радиуса 3, пересекающая стороны угла в точках
С центром в точке О построена окружность радиуса 3, пересекающая стороны угла в точках 

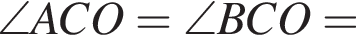

 Положительный корень этого уравнения
Положительный корень этого уравнения  Аналогично CB = CO. Что и требовалось доказать.
Аналогично CB = CO. Что и требовалось доказать. Радиус окружности равен 3, поэтому площадь сектора AOB равна
Радиус окружности равен 3, поэтому площадь сектора AOB равна 





 углы
углы  и
и  равны как вертикальные. Тогда треугольники AO2C и AO1B подобны, следовательно,
равны как вертикальные. Тогда треугольники AO2C и AO1B подобны, следовательно, 
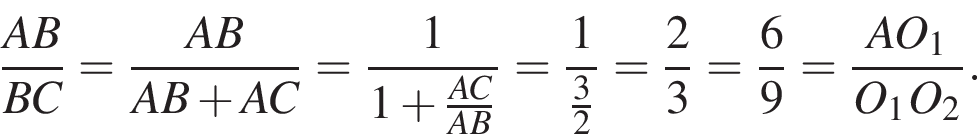









 По свойству секущей и касательной к окружности, проведённых из одной точки имеем
По свойству секущей и касательной к окружности, проведённых из одной точки имеем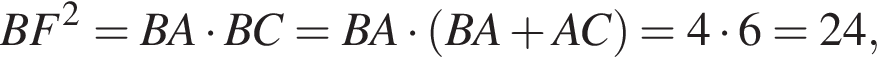



 прямоугольные треугольники ACD и ECB подобны по острому углу с коэффициентом подобия
прямоугольные треугольники ACD и ECB подобны по острому углу с коэффициентом подобия 
 тогда
тогда 


 а
а  Тогда
Тогда 




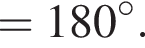
 из подобия треугольников MPQ и PQL получаем, что
из подобия треугольников MPQ и PQL получаем, что  откуда
откуда  Из неравенства о среднем арифметическом и среднем геометрическом получаем:
Из неравенства о среднем арифметическом и среднем геометрическом получаем:
 Таким образом,
Таким образом, 
 и
и 



 и
и  По свойству пересекающихся хорд получаем:
По свойству пересекающихся хорд получаем:


 Таким образом,
Таким образом,  следовательно,
следовательно, 


 откуда
откуда

 отсюда AM = DN, следовательно,
отсюда AM = DN, следовательно,  отсюда AN = DM.
отсюда AN = DM. откуда
откуда  Тогда
Тогда  По теореме косинусов для треугольника PAD получим:
По теореме косинусов для треугольника PAD получим:

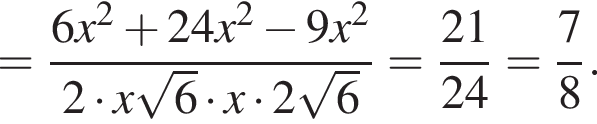


 Имеем:
Имеем:  откуда
откуда  тогда
тогда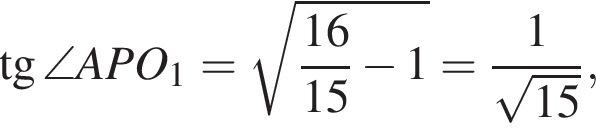
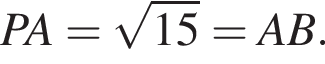 Найдем косинус угла BAD:
Найдем косинус угла BAD:



 Найдем площадь треугольника ABD:
Найдем площадь треугольника ABD:
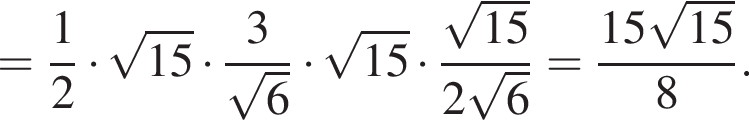





 и
и 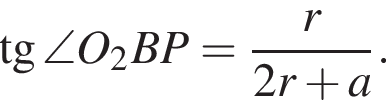 Заметим, что
Заметим, что 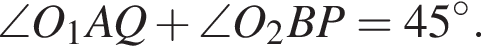 По формуле тангенса суммы получим:
По формуле тангенса суммы получим:



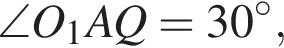
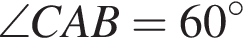 и
и 








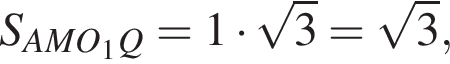




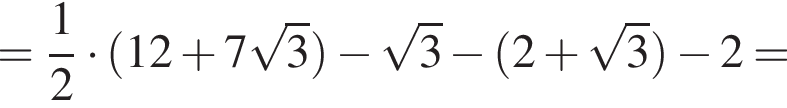


 поскольку отрезки KN и KM — диаметры соответствующих окружностей. Тогда треугольники NAK и MCK подобны по двум углам. Значит,
поскольку отрезки KN и KM — диаметры соответствующих окружностей. Тогда треугольники NAK и MCK подобны по двум углам. Значит,  откуда следует параллельность прямых AN и CM по признаку параллельности.
откуда следует параллельность прямых AN и CM по признаку параллельности. Пусть
Пусть 


 По теореме Пифагора в треугольнике BMK:
По теореме Пифагора в треугольнике BMK:



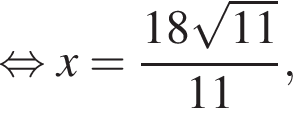

 то есть
то есть  а тогда
а тогда