1. Тип 13 № 500111 

Классификатор алгебры: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Методы алгебры: Формулы двойного угла
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
Уравнения. Тригонометрические уравнения, разложение на множители
i
а) Решите уравнение 
б) Найдите все корни этого уравнения, принадлежащие отрезку 
Решение. а) Запишем уравнение в виде






б) С помощью числовой окружности отберём корни, принадлежащие отрезку  Получим числа:
Получим числа: 
Ответ: а)  б)
б) 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Ответ: а)  б)
б) 
 б)
б) 
500111
а)  б)
б) 
 б)
б) 
Классификатор алгебры: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Методы алгебры: Формулы двойного угла
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения









 принадлежат корни
принадлежат корни  б)
б) 



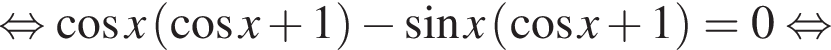

 то
то 
 то
то  При
При  решений нет. Разделим обе части уравнения на
решений нет. Разделим обе части уравнения на 

 принадлежат корни
принадлежат корни  б)
б) 








 Находим:
Находим:  б)
б) 
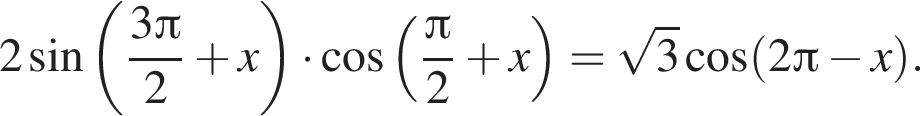


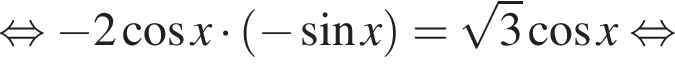




 б)
б) 







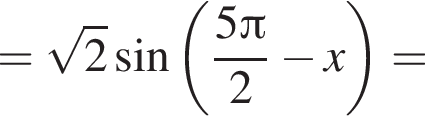














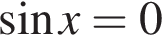 или
или  откуда
откуда  или
или  где
где 
 корни отберем с помощью единичной окружности. Получаем
корни отберем с помощью единичной окружности. Получаем 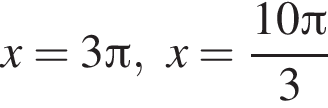 и
и 





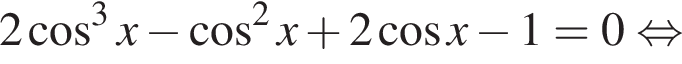








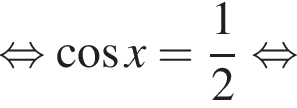
 Получим точку
Получим точку  б)
б) 




 не имеет корней. Имеем
не имеет корней. Имеем 
 то
то 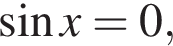 это невозможно. Это однородное уравнение первой степени, разделим обе его части на
это невозможно. Это однородное уравнение первой степени, разделим обе его части на 
 принадлежат корни
принадлежат корни  б)
б) 





 Получим числа
Получим числа 
 б)
б) 









 б)
б) 



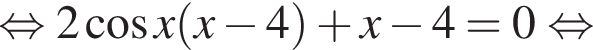





 б)
б) 




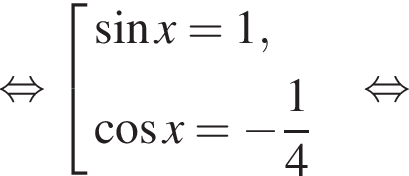



 б)
б) 




















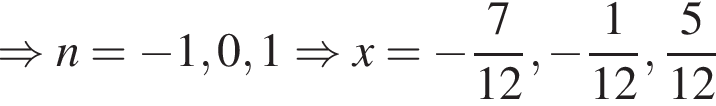









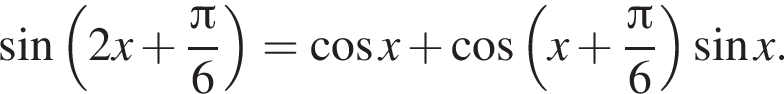

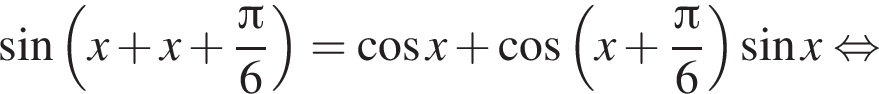
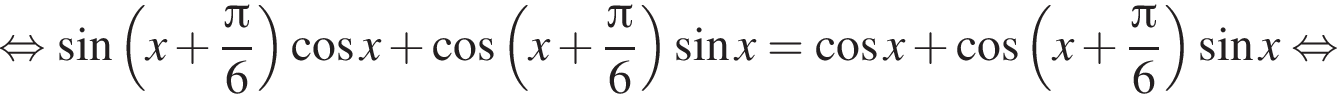
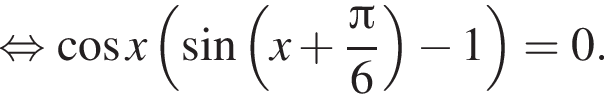
 или
или  откуда
откуда  или
или  где
где 

 где
где  б)
б) 



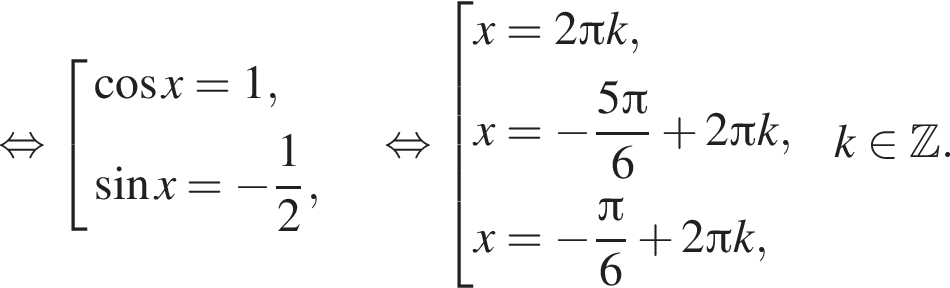
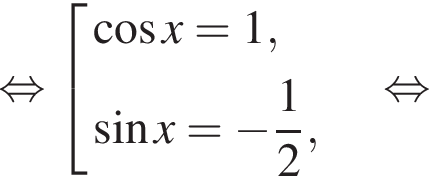


 б)
б) 




 откуда
откуда 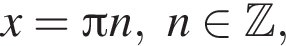 или
или  откуда
откуда  или
или 
 Получим числа
Получим числа 





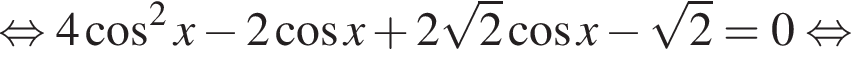





 б)
б) 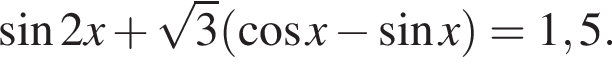











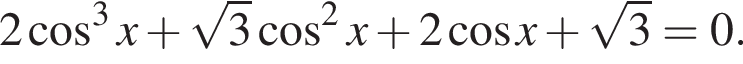











 б)
б) 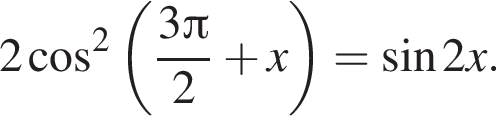









 б)
б) 








 б)
б) 

 Умножим на
Умножим на 

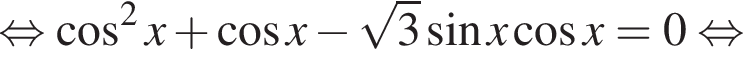


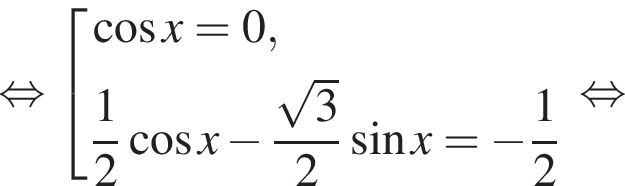





 б)
б) 








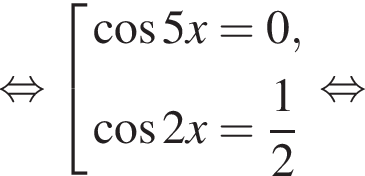

 б)
б) 

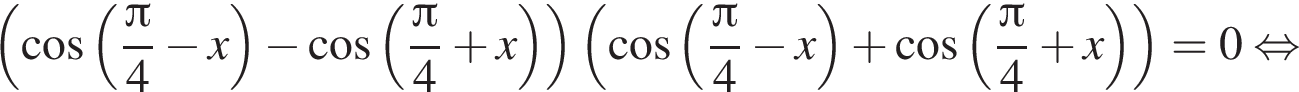

 Следовательно,
Следовательно, 
 Получим корни (см. рис.):
Получим корни (см. рис.): 
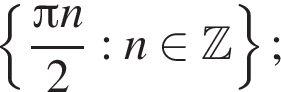 б)
б) 


 или
или  Из второго уравнения находим
Из второго уравнения находим  Следовательно,
Следовательно,  или
или 

 б)
б) 
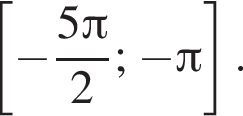

 отберём с помощью
отберём с помощью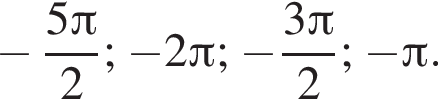












 с помощью неравенств:
с помощью неравенств:











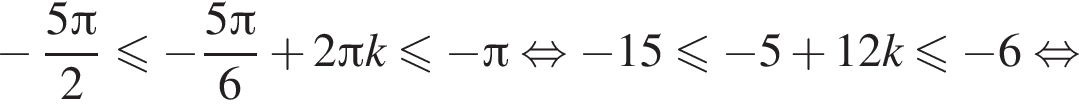

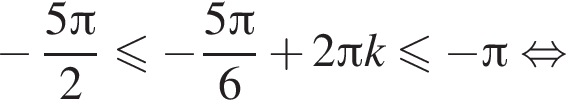



 где
где 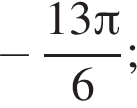
















 б)
б) 
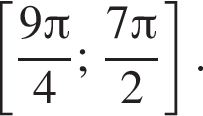

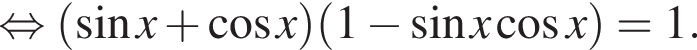

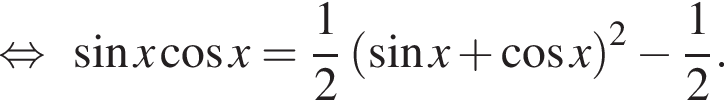


 получим уравнение
получим уравнение












 б)
б) 


 и
и  при любом x, следовательно, оба слагаемых не больше 0, поэтому их сумма может быть равна 0, только если слагаемые одновременно равны 0:
при любом x, следовательно, оба слагаемых не больше 0, поэтому их сумма может быть равна 0, только если слагаемые одновременно равны 0:

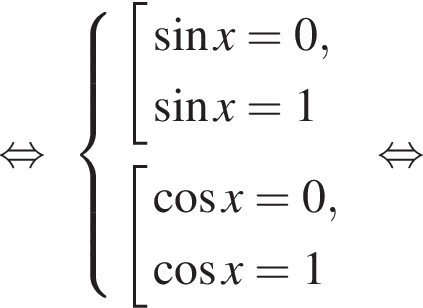



 Обозначим
Обозначим 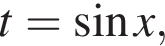 тогда
тогда 
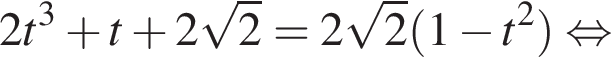








 б)
б)  записав левую часть в виде полного квадрата
записав левую часть в виде полного квадрата  Можно было найти дискриминант
Можно было найти дискриминант  и прийти к выводу, что уравнение имеет единственный корень
и прийти к выводу, что уравнение имеет единственный корень


 Обозначим
Обозначим 





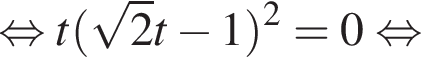



 б)
б) 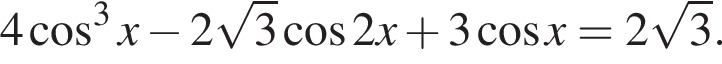

 Обозначим
Обозначим  тогда
тогда 
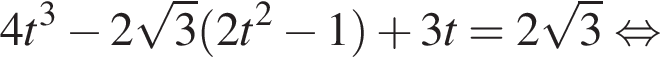







 б)
б) 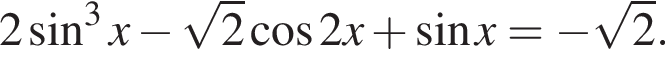
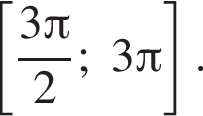

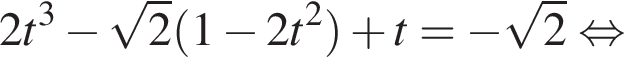


 б)
б) 
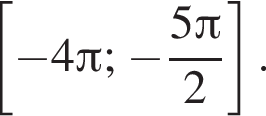







 с помощью тригонометрической окружности. Получаем числа:
с помощью тригонометрической окружности. Получаем числа: 
 б)
б) 

 получим:
получим: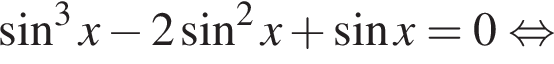
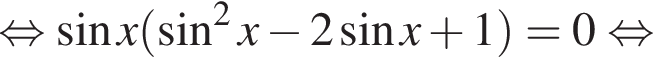




 равна
равна  б)
б) 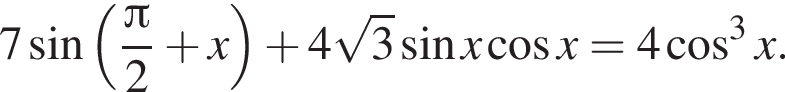

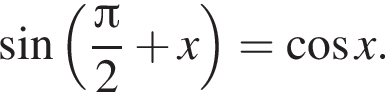 Далее вынесем общий множитель за скобки, воспользуемся основным тригонометрическим тождеством, заметим полный квадрат:
Далее вынесем общий множитель за скобки, воспользуемся основным тригонометрическим тождеством, заметим полный квадрат:


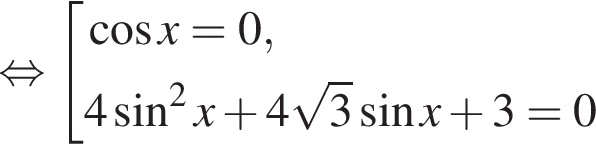



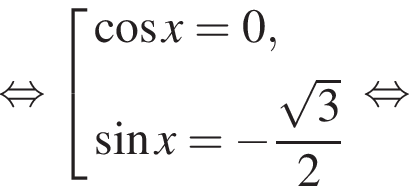
 равна
равна  и
и  Соседние члены второй и третьей серии отличаются на 2π, поэтому в заданный отрезок может попасть не более одного члена из каждой серии. Это числа
Соседние члены второй и третьей серии отличаются на 2π, поэтому в заданный отрезок может попасть не более одного члена из каждой серии. Это числа  но последнее в интервал не попадает.
но последнее в интервал не попадает. б)
б) 

 разложим на множители:
разложим на множители:








 б)
б) 



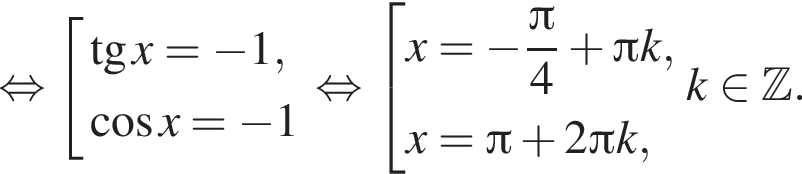
 б)
б) 





 отберем при помощи тригонометрической окружности (см. рис.). Подходит
отберем при помощи тригонометрической окружности (см. рис.). Подходит  б)
б) 



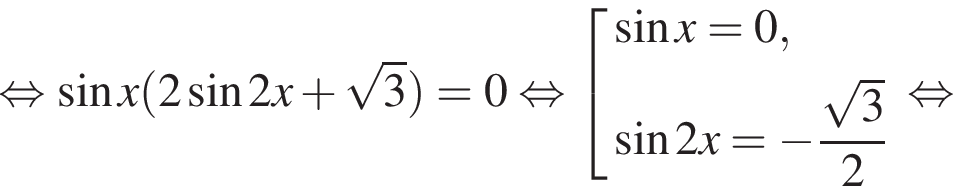

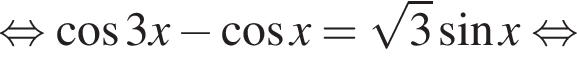






 б)
б) 








 при помощи тригонометрической окружности. Получим числа
при помощи тригонометрической окружности. Получим числа  б)
б) 










 б)
б) 
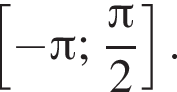







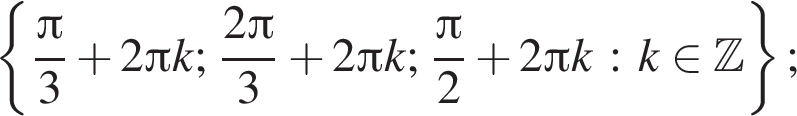 б)
б) 




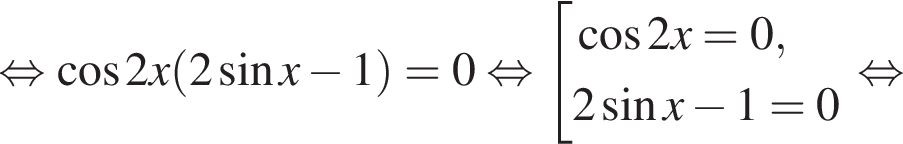








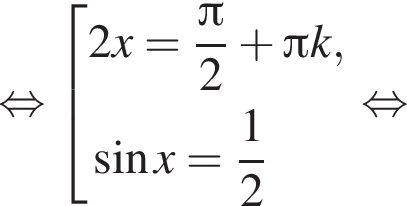
 б)
б) 

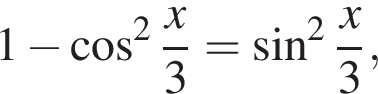



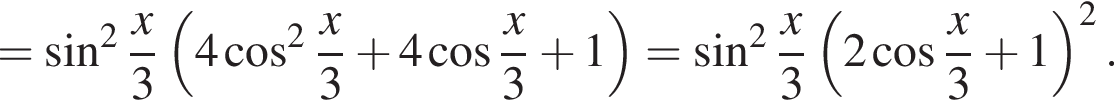










 б)
б) 

 тогда:
тогда:











 б) −2π.
б) −2π.

 и формулу синуса двойного угла
и формулу синуса двойного угла  получаем:
получаем:







 б)
б) 

 По формуле синуса двойного угла:
По формуле синуса двойного угла:  Тогда исходное уравнение примет вид
Тогда исходное уравнение примет вид  Выносим
Выносим 




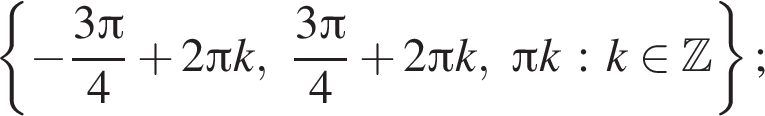 б)
б) 

 откуда получаем:
откуда получаем:




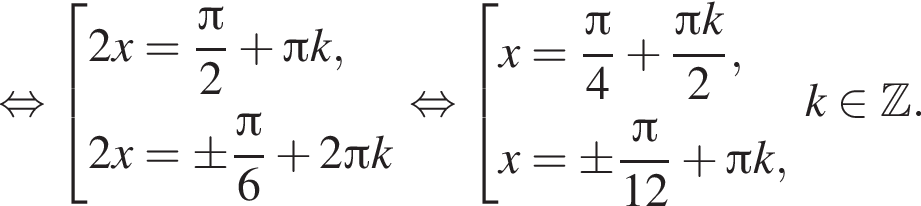





 Получим:
Получим: 



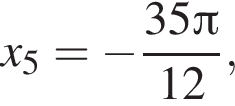
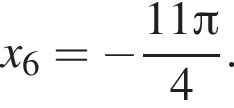
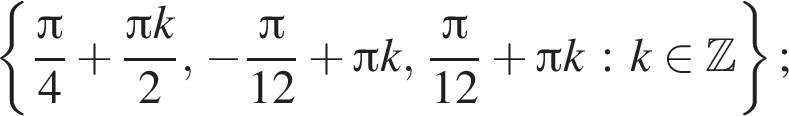
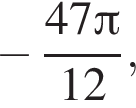





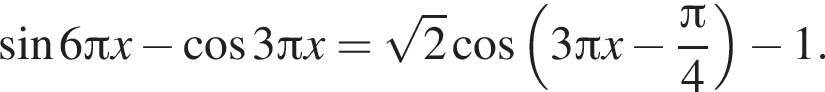





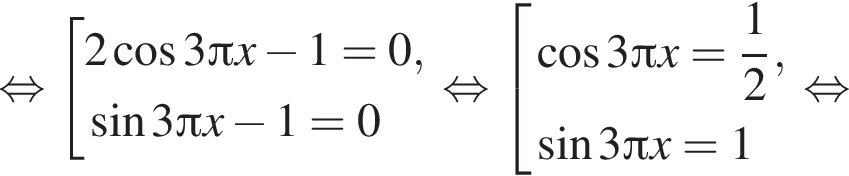




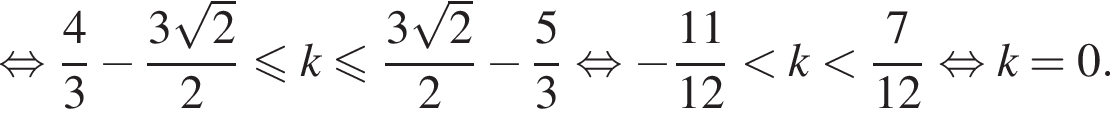








 б)
б) 












 б)
б) 









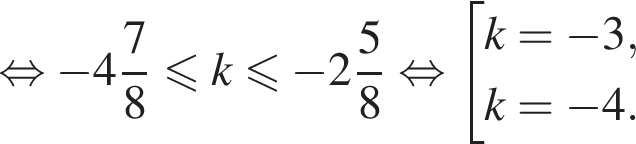

 б)
б) 






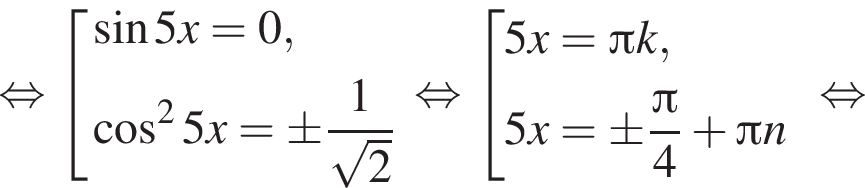







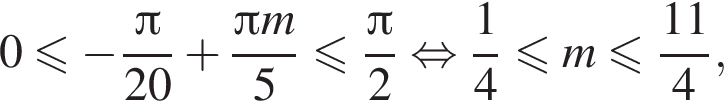











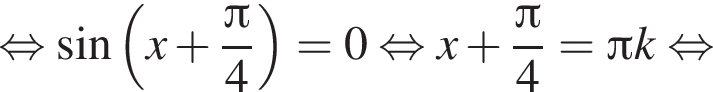


 с помощью тригонометрической окружности. Получим числа:
с помощью тригонометрической окружности. Получим числа: 



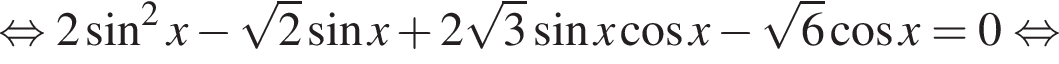



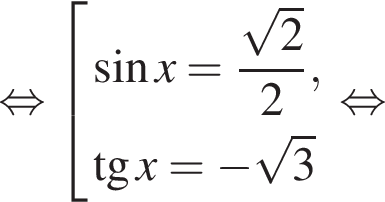









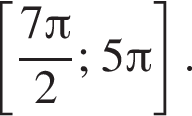








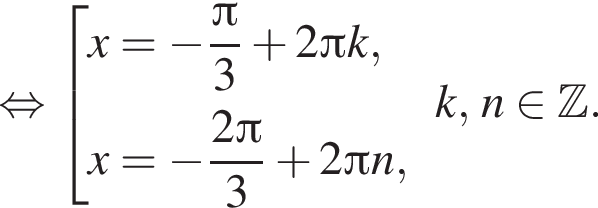

 находим:
находим:

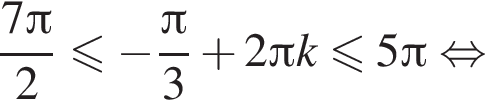





 получаем:
получаем:

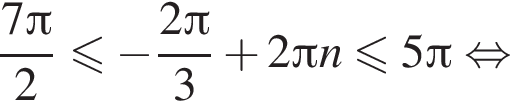
















 получаем:
получаем:



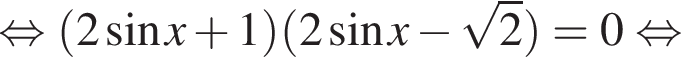



 принадлежат
принадлежат  б)
б) 









 б)
б) 





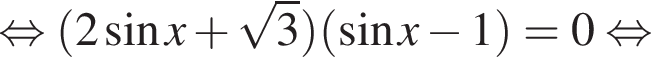
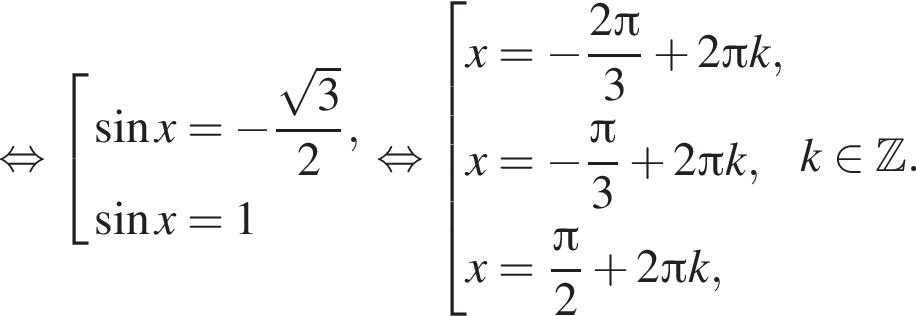


 б)
б) 







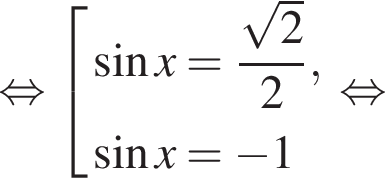


















 отберем при помощи тригонометрической окружности. Подходят
отберем при помощи тригонометрической окружности. Подходят 

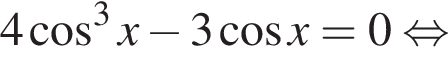


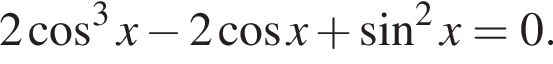

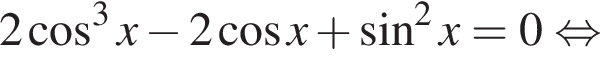

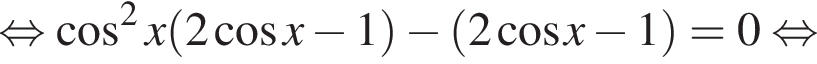







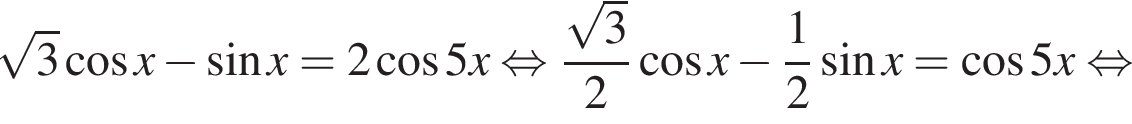



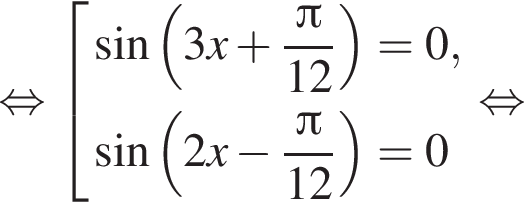
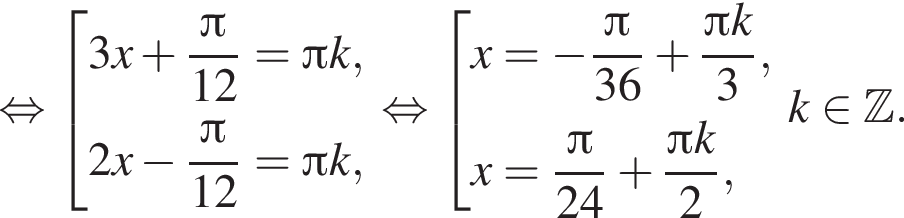





 отберем при помощи тригонометрической окружности (см. рис.). Подходят
отберем при помощи тригонометрической окружности (см. рис.). Подходят 













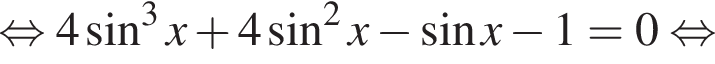








 равна
равна 






























 то есть при
то есть при  где
где 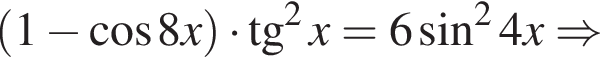
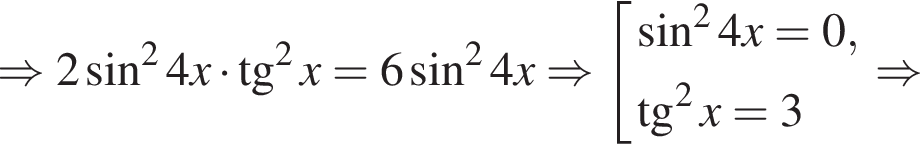


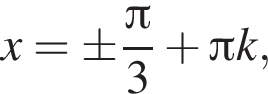
 отберем при помощи тригонометрической окружности (см. рис.). Подходят
отберем при помощи тригонометрической окружности (см. рис.). Подходят