
Дан куб ABCDA1B1C1D1 с ребром 1. Точка T — середина ребра AD.
а) Докажите, что плоскость A1BT делит объем куба в отношении 1 : 11.
б) Найдите расстояние от вершины A до плоскости A1BT.
Решение. а) Найдём объём пирамиды A1ATB, это одна из частей, на которые куб делится плоскостью A1BT. Он равен

поэтому объём второй части куба равен  Отсюда искомое отношение равно
Отсюда искомое отношение равно

что и требовалось доказать.
б) Пусть h — искомое расстояние. Найдём двумя способами объём пирамиды A1ATB. С одной стороны, из пункта а), он равен
![]() С другой стороны, он равен
С другой стороны, он равен  Треугольник A1BT — равнобедренный, его основание A1B равно
Треугольник A1BT — равнобедренный, его основание A1B равно ![]() а боковые стороны равны
а боковые стороны равны ![]() Если H — середина основания A1B, то
Если H — середина основания A1B, то  поэтому
поэтому  Следовательно, объём пирамиды A1ATB равен
Следовательно, объём пирамиды A1ATB равен  Приравняем выражения для объёма:
Приравняем выражения для объёма:
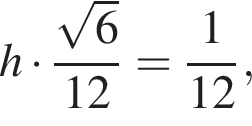
откуда 
Ответ: б) ![]()
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) ИЛИ имеется верное доказательство утверждения пункта а), и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а), ИЛИ при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | 1 |
| Решение не соответствует ни одному из критериев, приведённых выше | 0 |
| Максимальный балл | 3 |





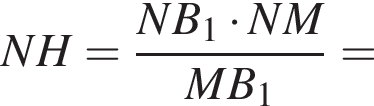



 Длины боковых рёбер пирамиды SA = 5, SB = 13, SD = 10.
Длины боковых рёбер пирамиды SA = 5, SB = 13, SD = 10. и
и  поэтому стороны SA и AB, SA и AD перпендикулярны, значит, ребро SA перпендикулярно плоскости основания пирамиды.
поэтому стороны SA и AB, SA и AD перпендикулярны, значит, ребро SA перпендикулярно плоскости основания пирамиды.
 как диагонали ромба. Значит, по теореме о трех перпендикулярах,
как диагонали ромба. Значит, по теореме о трех перпендикулярах, 
 Плоскость
Плоскость 




 тогда
тогда  пересекает плоскость
пересекает плоскость 


 в 12 раз меньше объема куба.
в 12 раз меньше объема куба. Он равен
Он равен 
 другим способом. Он равен
другим способом. Он равен  поэтому
поэтому  Следовательно, объём пирамиды
Следовательно, объём пирамиды  Приравняем выражения для объёма:
Приравняем выражения для объёма:  откуда
откуда 
 по прямой ML, параллельной прямым BC и
по прямой ML, параллельной прямым BC и  прямая LM перпендикулярна грани
прямая LM перпендикулярна грани  поэтому
поэтому  Используя пункт а), получаем, что
Используя пункт а), получаем, что  и, следовательно,
и, следовательно, 
 Найдём
Найдём 
 Значит, треугольник
Значит, треугольник 
 Отсюда следует, что расстояние от точки
Отсюда следует, что расстояние от точки 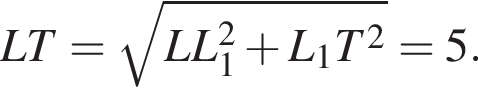 Найдём
Найдём 
 все рёбра равны 1.
все рёбра равны 1. 

 Поэтому
Поэтому
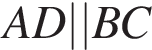 и AD — хорда основания, является искомым сечением.
и AD — хорда основания, является искомым сечением. Высота OF треугольника OPK лежит в плоскости OPK, следовательно,
Высота OF треугольника OPK лежит в плоскости OPK, следовательно,  и
и  значит,
значит, 





 сторона основания равна 2.
сторона основания равна 2.  — середина ребра SB.
— середина ребра SB.





 где h — искомое расстояние. В треугольнике SBC высота SM равна
где h — искомое расстояние. В треугольнике SBC высота SM равна 



 B1D = 2:
B1D = 2:

 значит, по теореме о трех перпендикулярах,
значит, по теореме о трех перпендикулярах,  Аналогично
Аналогично  Тогда, по признаку перпендикулярности прямой и плоскости,
Тогда, по признаку перпендикулярности прямой и плоскости, 
 Опустим перпендикуляр
Опустим перпендикуляр  Точка
Точка  Отрезок
Отрезок 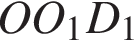 по теореме Пифагора найдём
по теореме Пифагора найдём 




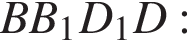

 и
и  следовательно,
следовательно,  — прямоугольник, откуда
— прямоугольник, откуда  Прямая HD1 — секущая при параллельных прямых BD и
Прямая HD1 — секущая при параллельных прямых BD и  равны. Из прямоугольного треугольника OBH найдём
равны. Из прямоугольного треугольника OBH найдём 

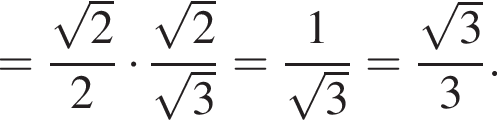
 и
и  равновелики.
равновелики.



 Ее объем можно выразить двумя способами:
Ее объем можно выразить двумя способами: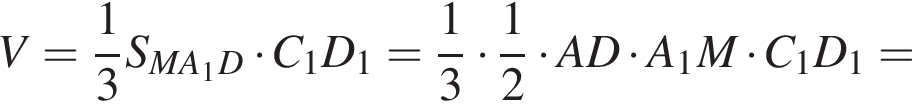
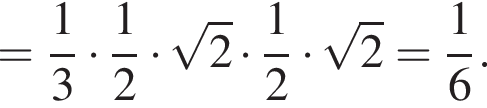
 где h — искомое расстояние.
где h — искомое расстояние. 
 Проведем в нем высоту
Проведем в нем высоту 



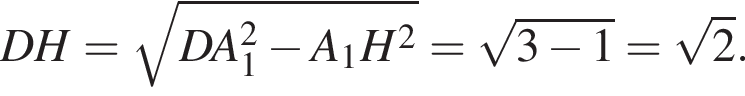



 Поскольку плоскость PQR перпендикулярна ребру SD, искомое расстояние равно DE.
Поскольку плоскость PQR перпендикулярна ребру SD, искомое расстояние равно DE. CP = 1. Проведём PL, проведём LR || AC,
CP = 1. Проведём PL, проведём LR || AC,  Проведём RK. Трапеция LPKR — искомое сечение. Сечение параллельно АС по признаку параллельности прямой к плоскости.
Проведём RK. Трапеция LPKR — искомое сечение. Сечение параллельно АС по признаку параллельности прямой к плоскости. 
 P(0; 5; 0),
P(0; 5; 0), 



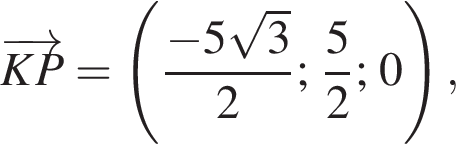




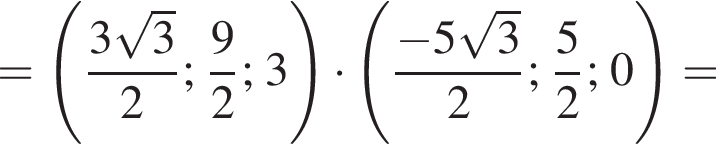





 и
и  получаем, что
получаем, что 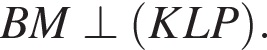
 подставив координаты точки К:
подставив координаты точки К:
 поэтому
поэтому 







 (ΔBKF ~ ΔBAT):
(ΔBKF ~ ΔBAT):
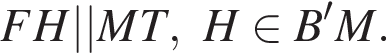 Тогда
Тогда 



 Тогда
Тогда  и
и 




 следовательно,
следовательно, 
 то
то  Пусть основанием перпендикуляра опущенного из T на γ будет являться точка S. Тогда TS || BM || F''F'. Таким образом, треугольники FTS и FF''F' будут подобны. Следовательно,
Пусть основанием перпендикуляра опущенного из T на γ будет являться точка S. Тогда TS || BM || F''F'. Таким образом, треугольники FTS и FF''F' будут подобны. Следовательно,  откуда
откуда 
 поэтому прямая сечения LL1 параллельна BD, где L1 лежит на B1C1. Сечением призмы будет трапеция
поэтому прямая сечения LL1 параллельна BD, где L1 лежит на B1C1. Сечением призмы будет трапеция 
 как диагонали квадрата таким образом по теореме о трех перпендикулярах
как диагонали квадрата таким образом по теореме о трех перпендикулярах  следовательно,
следовательно, 



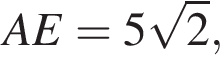
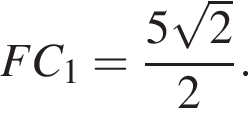
 Значит,
Значит,  Таким образом,
Таким образом, 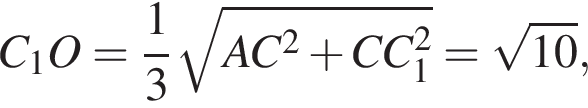


 Таким образом,
Таким образом, 
 в плоскости AA1C1C опустим перпендикуляр MH на прямую EF. Так как по доказанному в п. а)
в плоскости AA1C1C опустим перпендикуляр MH на прямую EF. Так как по доказанному в п. а)  плоскость
плоскость  следовательно, указанный перпендикуляр — искомое расстояние. Найдем
следовательно, указанный перпендикуляр — искомое расстояние. Найдем  Заметим,
Заметим,  Таким образом,
Таким образом, 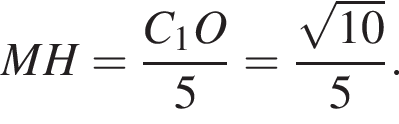





 Подставим найденные координаты в уравнение плоскости
Подставим найденные координаты в уравнение плоскости  получим:
получим:



 тогда
тогда  Следовательно,
Следовательно,
 Следовательно, векторы
Следовательно, векторы  до плоскости
до плоскости  определяется по формуле
определяется по формуле 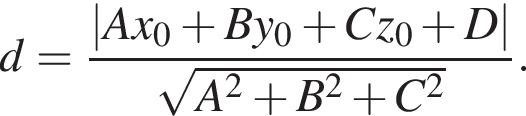
 получаем:
получаем:



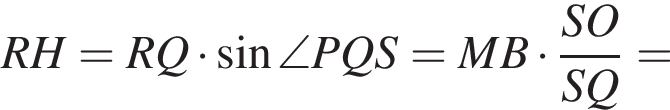




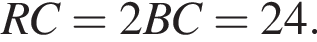
 следовательно,
следовательно,  Значит, М — середина СС1.
Значит, М — середина СС1.


 Значит,
Значит,  В треугольнике RPM находим стороны:
В треугольнике RPM находим стороны: 

 По теореме косинусов
По теореме косинусов






 уравнение плоскости APQ имеет вид
уравнение плоскости APQ имеет вид  Координаты точки М() с координатами
Координаты точки М() с координатами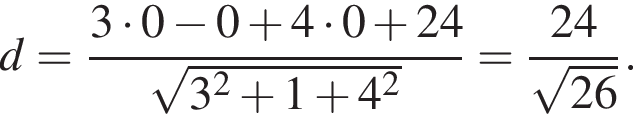




 получим:
получим:

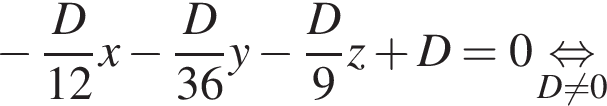











 Таким образом,
Таким образом,









 Точка Q — середина ребра A1B1, а точка P делит ребро B1C1 в отношении 1 : 2, считая от вершины C1. Плоскость APQ пересекает ребро CC1 в точке M.
Точка Q — середина ребра A1B1, а точка P делит ребро B1C1 в отношении 1 : 2, считая от вершины C1. Плоскость APQ пересекает ребро CC1 в точке M.










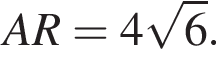


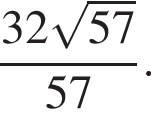

 AK — биссектриса, медиана и высота равнобедренного треугольника ABC. По теореме Пифагора AK =
AK — биссектриса, медиана и высота равнобедренного треугольника ABC. По теореме Пифагора AK =  то есть SH = 1, следовательно, из треугольника SAH по теореме Пифагора AH = 2. Тогда искомое расстояние равно 1.
то есть SH = 1, следовательно, из треугольника SAH по теореме Пифагора AH = 2. Тогда искомое расстояние равно 1. и
и  Приравнивая объемы, получаем
Приравнивая объемы, получаем 
 Осталось найти площади треугольников ABC и SCB.
Осталось найти площади треугольников ABC и SCB.



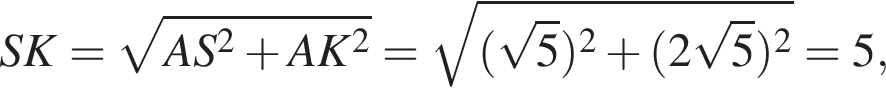



 Таким образом, по доказанному в п. а), искомое расстояние равно 1.
Таким образом, по доказанному в п. а), искомое расстояние равно 1. Пусть прямая CE пересекает ребро AB в точке M. Треугольники BME и DCE подобны, поэтому
Пусть прямая CE пересекает ребро AB в точке M. Треугольники BME и DCE подобны, поэтому  откуда
откуда  Тогда
Тогда  Треугольники ABS и AMF подобны, значит,
Треугольники ABS и AMF подобны, значит,  Поэтому прямая SB параллельна плоскости CEF.
Поэтому прямая SB параллельна плоскости CEF. Тогда
Тогда  Пусть O — центр основания ABCD. Так как все боковые ребра пирамиды равны, SO — высота пирамиды. Имеем:
Пусть O — центр основания ABCD. Так как все боковые ребра пирамиды равны, SO — высота пирамиды. Имеем:




 Что и требовалось доказать.
Что и требовалось доказать.










 С другой стороны,
С другой стороны,  где ha и hl — высоты, проведенные из соответствующих вершин. Таким образом, ha является искомым расстоянием.
где ha и hl — высоты, проведенные из соответствующих вершин. Таким образом, ha является искомым расстоянием.

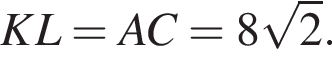
 Вычислим площадь треугольника ABK:
Вычислим площадь треугольника ABK:  найдем
найдем  Получаем:
Получаем: 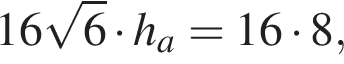 откуда
откуда 
 В прямоугольном треугольнике QAM катет
В прямоугольном треугольнике QAM катет  короче гипотенузы QM = x, поэтому
короче гипотенузы QM = x, поэтому  то есть
то есть 
 то есть
то есть  Тогда
Тогда 
 и
и  Поскольку
Поскольку 




 а значит,
а значит,  и
и  Отрезки
Отрезки  и
и  отрезок FG параллелен отрезку MB. Пусть плоскость GEF пересекает отрезок MD в точке K. Так как прямая FG параллельна MB, по признаку параллельности прямой и плоскости FG параллельна плоскости MBD. Плоскость MBD и секущая плоскость пересекаются по прямой KE, и по свойству параллельных прямой и плоскости прямая KE параллельна FG и, следовательно, параллельна MB. Треугольники DKE и DMB подобны, поэтому
отрезок FG параллелен отрезку MB. Пусть плоскость GEF пересекает отрезок MD в точке K. Так как прямая FG параллельна MB, по признаку параллельности прямой и плоскости FG параллельна плоскости MBD. Плоскость MBD и секущая плоскость пересекаются по прямой KE, и по свойству параллельных прямой и плоскости прямая KE параллельна FG и, следовательно, параллельна MB. Треугольники DKE и DMB подобны, поэтому 
 и
и  Плоскость GEF пересекает грань CMD по отрезку CK. Угол CMK равен 60°, поскольку
Плоскость GEF пересекает грань CMD по отрезку CK. Угол CMK равен 60°, поскольку 


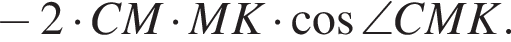
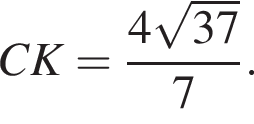


 Тогда
Тогда 

 В четырёхугольник KLMN можно вписать окружность, поэтому
В четырёхугольник KLMN можно вписать окружность, поэтому
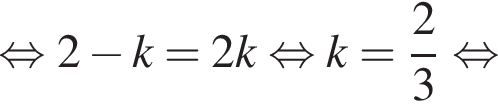








 откуда
откуда



 откуда
откуда
 а значит, прямая CD параллельна плоскости ABP и поэтому CD не имеет общих точек с прямой PK, лежащей в плоскости сечения. Так как PK и CD не имеют общих точек и лежат в плоскости SCD, они параллельны.
а значит, прямая CD параллельна плоскости ABP и поэтому CD не имеет общих точек с прямой PK, лежащей в плоскости сечения. Так как PK и CD не имеют общих точек и лежат в плоскости SCD, они параллельны. и
и  следует, прямая PK параллельна прямой AB, а следовательно, и всей плоскости ABS. Значит, расстояние от любой точки прямой PK до плоскости ABS будет одинаковым. Найдём это расстояние от точки пересечения PK и SN — точки E.
следует, прямая PK параллельна прямой AB, а следовательно, и всей плоскости ABS. Значит, расстояние от любой точки прямой PK до плоскости ABS будет одинаковым. Найдём это расстояние от точки пересечения PK и SN — точки E. и
и  откуда следует, что четырехугольник ADNL — прямоугольник и
откуда следует, что четырехугольник ADNL — прямоугольник и 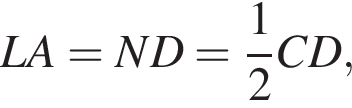 то есть L — середина AB.
то есть L — середина AB. Поскольку прямая AB перпендикулярна пересекающимся прямым LN и SL, она перпендикулярна плоскости SNL, а раз AB лежит в плоскости ABS, плоскости ABS и SNL перпендикулярны. Тогда перпендикуляры NT и EF к плоскости ABS из точек N и E плоскости SNL попадут на прямую их пересечения SL.
Поскольку прямая AB перпендикулярна пересекающимся прямым LN и SL, она перпендикулярна плоскости SNL, а раз AB лежит в плоскости ABS, плоскости ABS и SNL перпендикулярны. Тогда перпендикуляры NT и EF к плоскости ABS из точек N и E плоскости SNL попадут на прямую их пересечения SL. ) и катету (
) и катету ( ), поэтому другие катеты SN и SL также равны. Рассмотрим равнобедренный треугольник SNL, в котором
), поэтому другие катеты SN и SL также равны. Рассмотрим равнобедренный треугольник SNL, в котором  основание
основание  а высота и медиана к нему
а высота и медиана к нему  По теореме Пифагора для треугольника LHS найдём
По теореме Пифагора для треугольника LHS найдём


 откуда
откуда  поэтому
поэтому 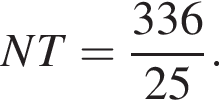 В прямоугольном треугольнике SNT с прямым углом T отрезок EF перпендикулярен ST и проходит через середину SN, а значит, является средней линией треугольника SNT, поэтому
В прямоугольном треугольнике SNT с прямым углом T отрезок EF перпендикулярен ST и проходит через середину SN, а значит, является средней линией треугольника SNT, поэтому 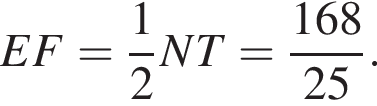
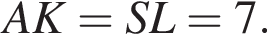
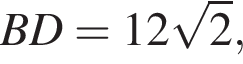

 откуда
откуда 
 Далее, BL = 10,
Далее, BL = 10,  следовательно, прямая LM параллельна прямой SO — высоте пирамиды. Значит, прямая LM перпендикулярна плоскости ABC. Таким образом, плоскость CKL перпендикулярна плоскости ABC по признаку перпендикулярности плоскостей.
следовательно, прямая LM параллельна прямой SO — высоте пирамиды. Значит, прямая LM перпендикулярна плоскости ABC. Таким образом, плоскость CKL перпендикулярна плоскости ABC по признаку перпендикулярности плоскостей.







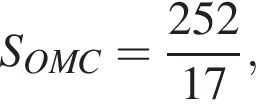

 Точки F, N — середины сторон A1B1 и B1C1 соответственно.
Точки F, N — середины сторон A1B1 и B1C1 соответственно. 
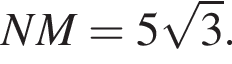 Пусть F1 — проекция точки F на ABC, K и K1 — точки пересечения прямых CF1 и DE, C1F и MN соответственно, O — точка пересечения прямых CF и KK1. Имеем:
Пусть F1 — проекция точки F на ABC, K и K1 — точки пересечения прямых CF1 и DE, C1F и MN соответственно, O — точка пересечения прямых CF и KK1. Имеем:






 откуда
откуда
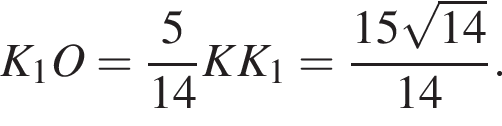





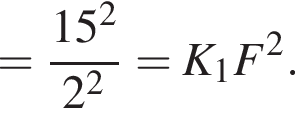



 и, следовательно,
и, следовательно,  Отрезок ML в нём является медианой из вершины прямого угла, следовательно,
Отрезок ML в нём является медианой из вершины прямого угла, следовательно,  Аналогично, из равенства боковых граней, следует, что MK = 3, следовательно, треугольник KLM — равносторонний.
Аналогично, из равенства боковых граней, следует, что MK = 3, следовательно, треугольник KLM — равносторонний. и
и  а значит, прямые PG и CH перпендикулярны плоскости KLM и CH является искомым расстоянием. При этом R — середина CP и прямоугольные треугольники PRG и CRH равны. Имеем:
а значит, прямые PG и CH перпендикулярны плоскости KLM и CH является искомым расстоянием. При этом R — середина CP и прямоугольные треугольники PRG и CRH равны. Имеем:

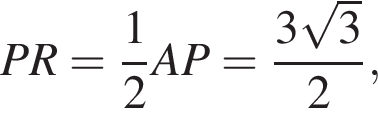




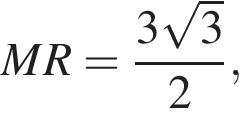

 откуда
откуда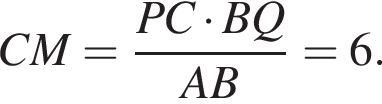

 Далее находим:
Далее находим:





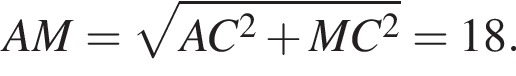

 Следовательно,
Следовательно, 
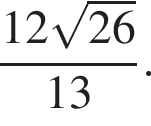
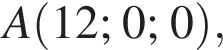



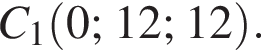
 Составим уравнение плоскости APQ в виде
Составим уравнение плоскости APQ в виде 





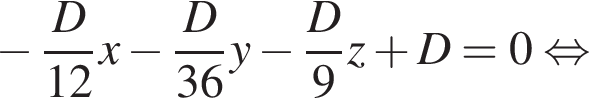





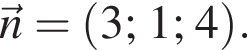





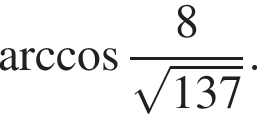

 откуда
откуда
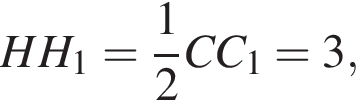
















 откуда вектор нормали
откуда вектор нормали 







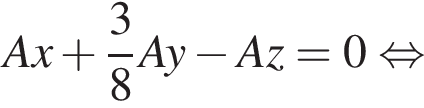



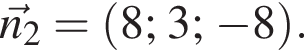






 её вектор нормали
её вектор нормали  Найдём расстояние между точкой A и плоскостью BD1Q:
Найдём расстояние между точкой A и плоскостью BD1Q:




 следовательно, прямые EK и PM параллельны. Таким образом, плоскости EFK и MPQ содержат две пары пересекающихся параллельных прямых и, следовательно, параллельны.
следовательно, прямые EK и PM параллельны. Таким образом, плоскости EFK и MPQ содержат две пары пересекающихся параллельных прямых и, следовательно, параллельны.




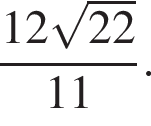





 Гипотенуза SC прямоугольного треугольника CSD в 2 раза больше проведённой к ней медианы DM. Поэтому
Гипотенуза SC прямоугольного треугольника CSD в 2 раза больше проведённой к ней медианы DM. Поэтому  Найдём катет SD этого треугольника:
Найдём катет SD этого треугольника:


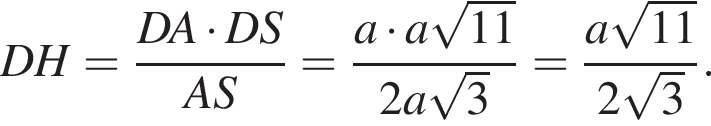






 a значит, прямоугольные треугольники
a значит, прямоугольные треугольники 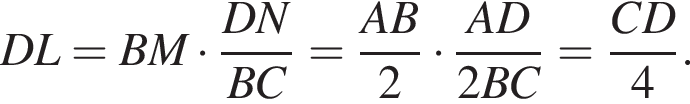
 поскольку прямая B1N перпендикулярна прямой NL, параллельной прямой CM. Пусть ребро куба равно a. Получаем:
поскольку прямая B1N перпендикулярна прямой NL, параллельной прямой CM. Пусть ребро куба равно a. Получаем: 






 получаем:
получаем: 





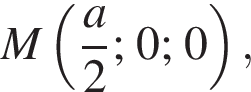






 поэтому
поэтому 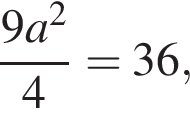 откуда
откуда  то есть
то есть 


 к плоскости α, уравнение которой запишем в виде
к плоскости α, уравнение которой запишем в виде  Нормаль перпендикулярна вектору
Нормаль перпендикулярна вектору  Подставим в уравнение плоскости координаты точек N, B1 и решим систему уравнений:
Подставим в уравнение плоскости координаты точек N, B1 и решим систему уравнений: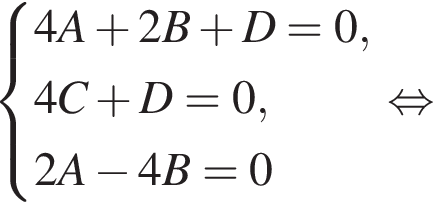

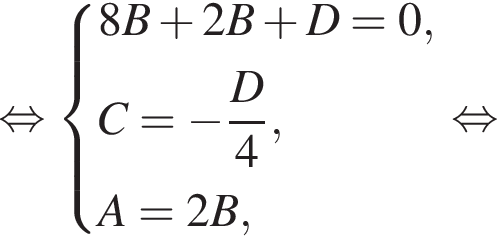

 тогда
тогда 




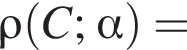




 и
и  следовательно,
следовательно,
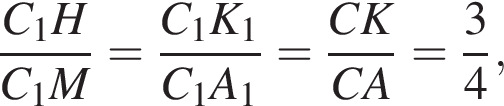




 откуда находим, что
откуда находим, что 

 Запишем необходимые координаты:
Запишем необходимые координаты: 











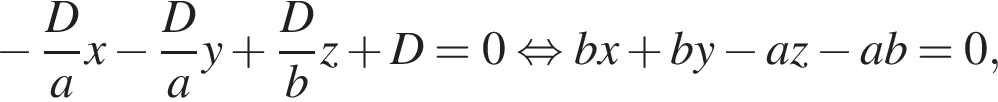
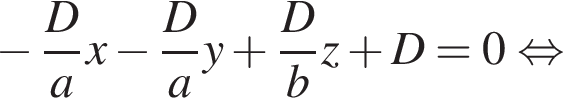


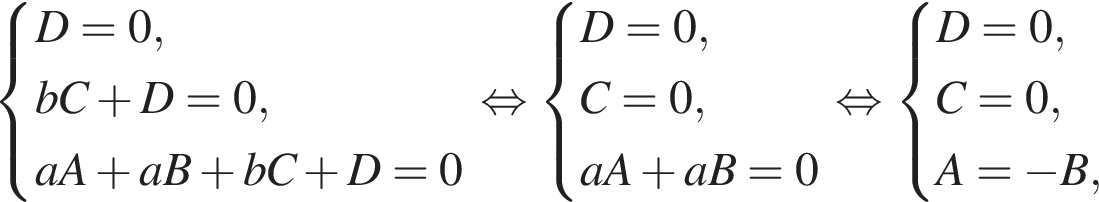





 Найдём скалярное поизведение:
Найдём скалярное поизведение:




 плоскость AD1C задаётся уравнением
плоскость AD1C задаётся уравнением  её вектор нормали
её вектор нормали  Найдём расстояние между точкой
Найдём расстояние между точкой 


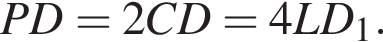 Тогда
Тогда 

 Находим:
Находим: 




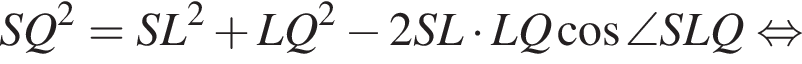




















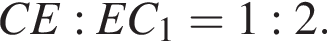
 Имеем:
Имеем:
 Теперь применим формулу для вычисления расстояния от точки до плоскости:
Теперь применим формулу для вычисления расстояния от точки до плоскости:
 а KLMN — квадрат со стороной 3.
а KLMN — квадрат со стороной 3. 
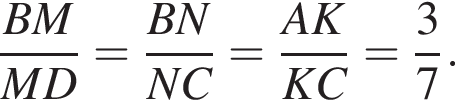

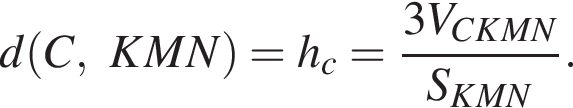

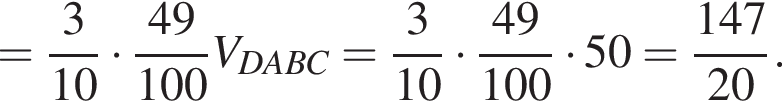








 Также на ребрах AD, BD и BC выбраны точки L, M и N соответственно так, что KLMN — квадрат со стороной 3.
Также на ребрах AD, BD и BC выбраны точки L, M и N соответственно так, что KLMN — квадрат со стороной 3. 






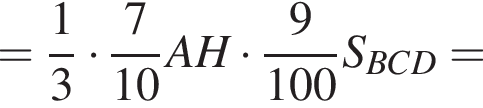
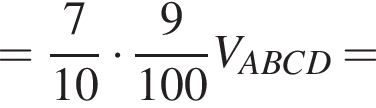


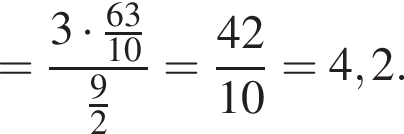










 Следовательно,
Следовательно, 
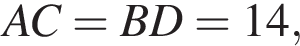
 и
и 
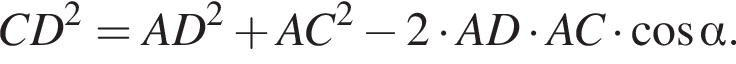







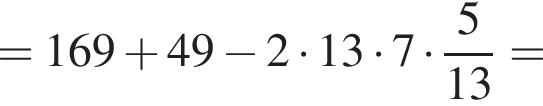

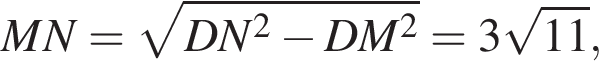



 и
и 










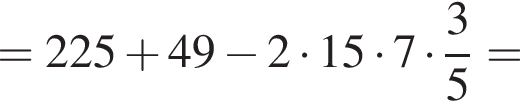

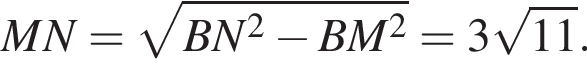



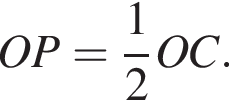 В плоскости SFC проведем прямую PQ. Пусть M' — точка пересечения прямой PQ с ребром SC. Заметим, что точка M' лежит в плоскости ANKE. Запишем теорему Менелая для треугольника SCO и прямой PQ:
В плоскости SFC проведем прямую PQ. Пусть M' — точка пересечения прямой PQ с ребром SC. Заметим, что точка M' лежит в плоскости ANKE. Запишем теорему Менелая для треугольника SCO и прямой PQ:



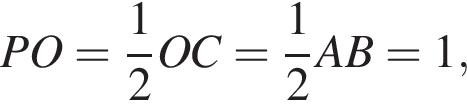

 тогда
тогда











 Тогда
Тогда 

 и
и  На ребрах AA1 и CD отмечены точки
На ребрах AA1 и CD отмечены точки  Таким образом, прямоугольные треугольники MKD и PBA подобны. Тогда
Таким образом, прямоугольные треугольники MKD и PBA подобны. Тогда  и
и  откуда
откуда



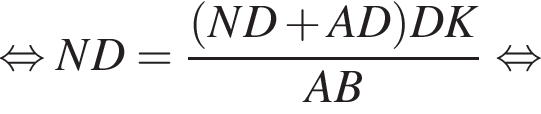






 точка N лежит на диагонали CB1 боковой грани CC1B1B. Прямые
точка N лежит на диагонали CB1 боковой грани CC1B1B. Прямые 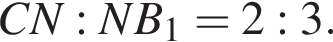





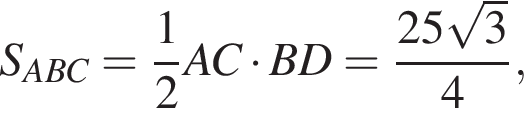

 откуда
откуда 






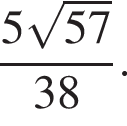
 откуда
откуда
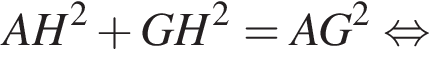










 и
и 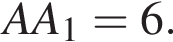 Через точки B1 и D параллельно прямой AC проведена плоскость, пересекающая ребро CC1 в точке K.
Через точки B1 и D параллельно прямой AC проведена плоскость, пересекающая ребро CC1 в точке K.  Треугольники B1C1K и AMD равны по катету и гипотенузе, поэтому
Треугольники B1C1K и AMD равны по катету и гипотенузе, поэтому  Значит, K — середина CC1.
Значит, K — середина CC1.





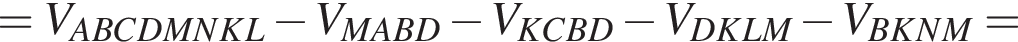





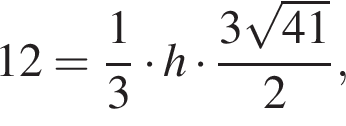 где h — искомое расстояние. Находим:
где h — искомое расстояние. Находим:

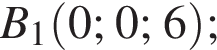






 Пусть α — плоскость, проходящая через точки B1 и D параллельно стороне AC. Уравнение плоскости имеет вид
Пусть α — плоскость, проходящая через точки B1 и D параллельно стороне AC. Уравнение плоскости имеет вид  —
—  то есть
то есть 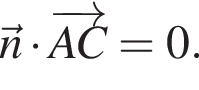 Запишем систему:
Запишем систему:

 и
и  Тогда
Тогда  а потому уравнение плоскости α принимает вид
а потому уравнение плоскости α принимает вид
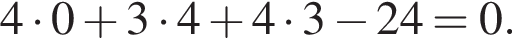




 также известно, что
также известно, что  Отсюда следует, что
Отсюда следует, что  и
и  Пусть плоскости
Пусть плоскости  Прямая AS параллельна плоскости OMK, значит, прямая AS не имеет общих точек с прямой EF, при этом прямые
Прямая AS параллельна плоскости OMK, значит, прямая AS не имеет общих точек с прямой EF, при этом прямые  Найдем боковое ребро:
Найдем боковое ребро:
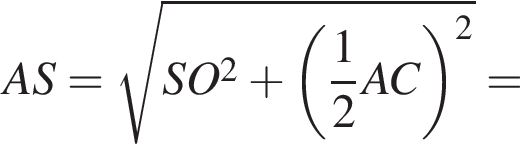


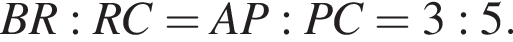
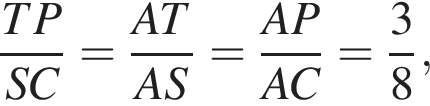
 Аналогично AB = 8.
Аналогично AB = 8. 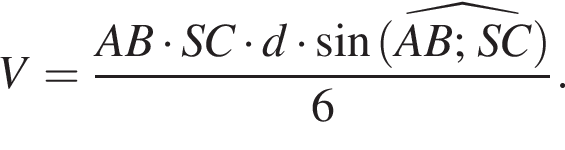
 откуда
откуда 

 Найдите расстояние от вершины S пирамиды до плоскости BKM.
Найдите расстояние от вершины S пирамиды до плоскости BKM.



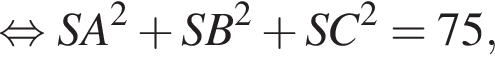
 то есть боковые ребра пирамиды равны, а в ее основании лежит правильный треугольник. Такая пирамида называется правильной.
то есть боковые ребра пирамиды равны, а в ее основании лежит правильный треугольник. Такая пирамида называется правильной. Из условия
Из условия  Тогда
Тогда 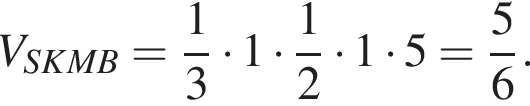 По теореме Пифагора в треугольнике BKM
По теореме Пифагора в треугольнике BKM

 Следовательно,
Следовательно,
 то есть
то есть 
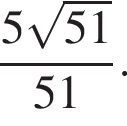
 Значит, PA = AD, а тогда по двум сторонам и углу между ними равны треугольники
Значит, PA = AD, а тогда по двум сторонам и углу между ними равны треугольники  и точки P, L, C лежат на одной прямой. Тогда точки K, M, L и C лежат в одной плоскости — плоскости α.
и точки P, L, C лежат на одной прямой. Тогда точки K, M, L и C лежат в одной плоскости — плоскости α.







 откуда
откуда  Найдем стороны треугольника PKL: сторону PL по теореме косинусов в треугольнике PAL, а стороны
Найдем стороны треугольника PKL: сторону PL по теореме косинусов в треугольнике PAL, а стороны 






 то по теореме косинусов в треугольнике PLK
то по теореме косинусов в треугольнике PLK
 и площадь треугольника PLK равна
и площадь треугольника PLK равна

 то по теореме косинусов в треугольнике PLK
то по теореме косинусов в треугольнике PLK
 и площадь треугольника PLK равна
и площадь треугольника PLK равна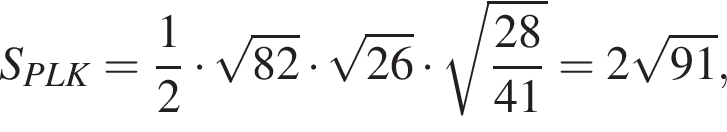







 Отрезок MC — средняя линия треугольника KC1P, следовательно, отрезки CC1 и CP равны. Тогда прямая B1P должна пересекать BC в середине, значит, точка N лежит на прямой B1P, а потому лежит в плоскости KMN.
Отрезок MC — средняя линия треугольника KC1P, следовательно, отрезки CC1 и CP равны. Тогда прямая B1P должна пересекать BC в середине, значит, точка N лежит на прямой B1P, а потому лежит в плоскости KMN.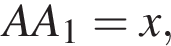 тогда высота пирамиды C1KB1P, проведенная из точки C, тоже равна x. Выразим объем пирамиды C1KB1P двумя способами:
тогда высота пирамиды C1KB1P, проведенная из точки C, тоже равна x. Выразим объем пирамиды C1KB1P двумя способами:








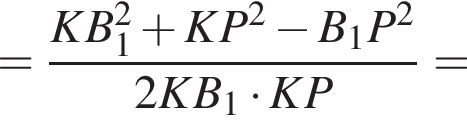








 то есть точка O — центр правильного треугольника ABC. Отсюда и следует, что пирамида ABCD правильная.
то есть точка O — центр правильного треугольника ABC. Отсюда и следует, что пирамида ABCD правильная.









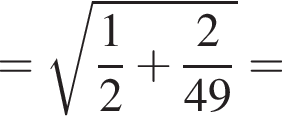






 находим:
находим:
 АА1 = 20, АС = 16.
АА1 = 20, АС = 16. тогда точка K — середина отрезка PL. Значит, точка P лежит в плоскости сечения. Пусть прямая PM пересекает ребро призмы AB в точке N, которая также лежит в плоскости сечения, а прямая NL пересекает ребро BB1 в точке T. Треугольники PCM и NBM подобны по двум углам, следовательно,
тогда точка K — середина отрезка PL. Значит, точка P лежит в плоскости сечения. Пусть прямая PM пересекает ребро призмы AB в точке N, которая также лежит в плоскости сечения, а прямая NL пересекает ребро BB1 в точке T. Треугольники PCM и NBM подобны по двум углам, следовательно,








 Аналогично получаем
Аналогично получаем  Пусть уравнение плоскости KLM имеет вид
Пусть уравнение плоскости KLM имеет вид  Подставим известные координаты и получим:
Подставим известные координаты и получим:
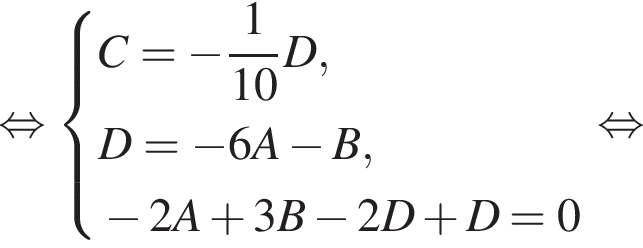









 Следовательно,
Следовательно,  и
и  где точка O — центр основания пирамиды.
где точка O — центр основания пирамиды. 



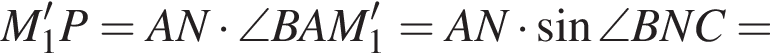


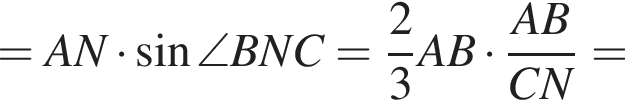















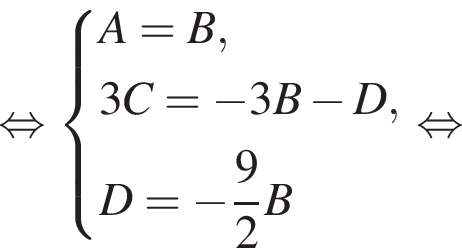

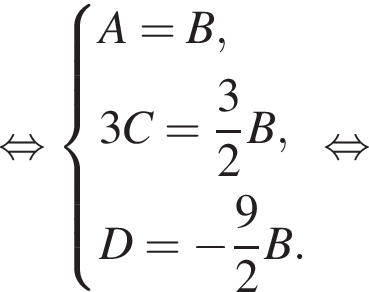

 Эта плоскость не параллельна оси ординат и не содержит ее, а потому
Эта плоскость не параллельна оси ординат и не содержит ее, а потому 



