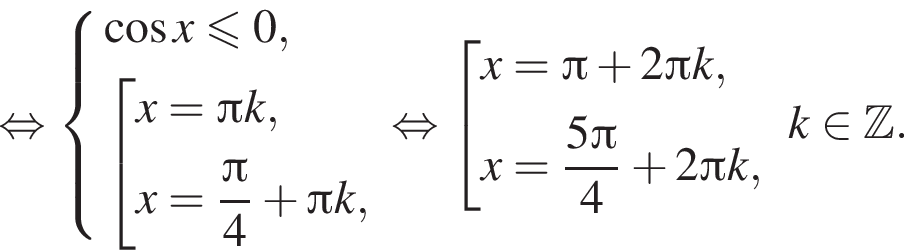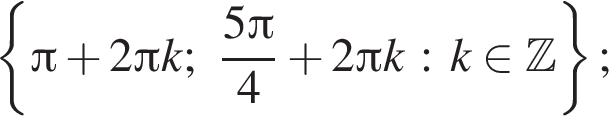1. Тип 13 № 501689 

Источники:
Классификатор алгебры: Однородные тригонометрические уравнения, Уравнения смешанного типа
Методы алгебры: Сведение к однородному
Кодификатор ФИПИ/Решу ЕГЭ:
Уравнения. Тригонометрия и показательные выражения
i
а) Решите уравнение 
б) Найдите все корни этого уравнения, принадлежащие отрезку 
Решение. а) Преобразуем исходное уравнение:






б) С помощью числовой окружности отберем корни, принадлежащие отрезку  Получим числа:
Получим числа: 
Ответ: а)  б)
б) 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Ответ: а)  б)
б) 
 б)
б) 
501689
а)  б)
б) 
 б)
б) 
Классификатор алгебры: Однородные тригонометрические уравнения, Уравнения смешанного типа
Методы алгебры: Сведение к однородному
Кодификатор ФИПИ/Решу ЕГЭ:
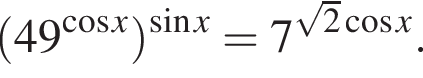






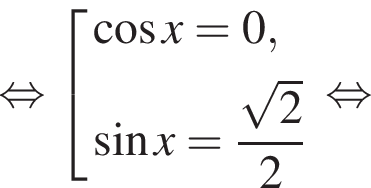


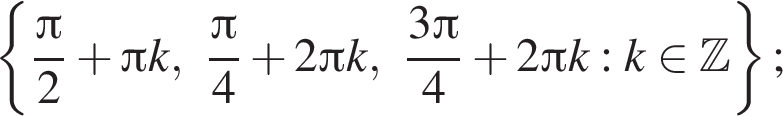 б)
б) 


 Далее имеем:
Далее имеем:





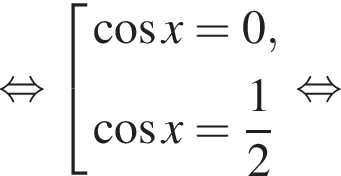
 для каждой из полученных серий корней находим, что заданному промежутку принадлежат числа
для каждой из полученных серий корней находим, что заданному промежутку принадлежат числа  и только они.
и только они.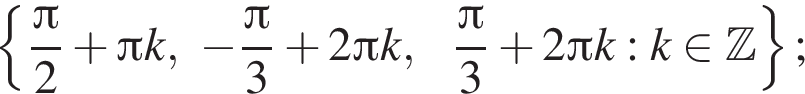 б)
б) 






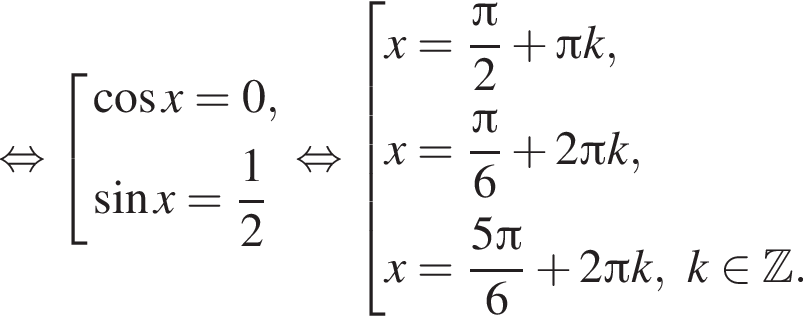

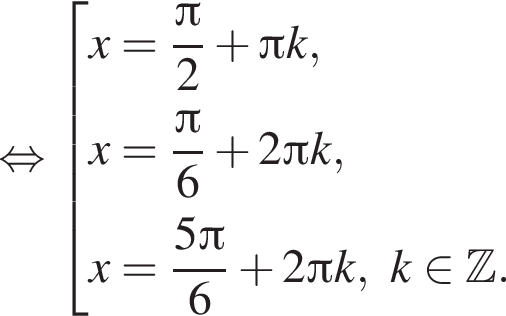

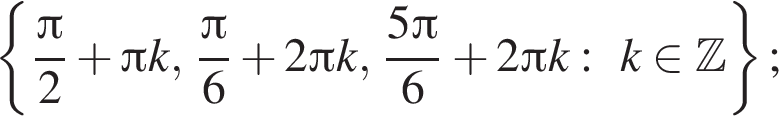 б)
б) 


 тогда исходное уравнение запишется в виде
тогда исходное уравнение запишется в виде 


 Получим числа:
Получим числа: 
 б)
б) 


 тогда исходное уравнение можно преобразовать так:
тогда исходное уравнение можно преобразовать так: 











 б)
б) 
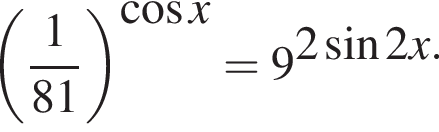









 б)
б) 


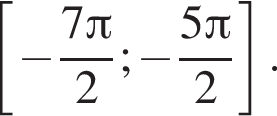







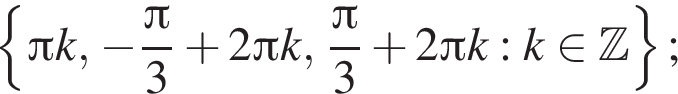 б)
б) 

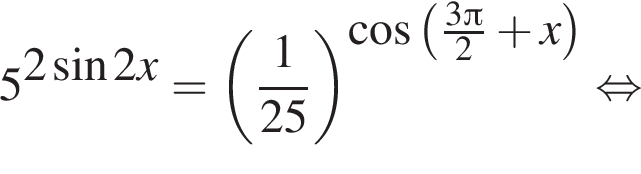







 удовлетворяют только числа
удовлетворяют только числа 
 б)
б) 



 что невозможно, или
что невозможно, или  откуда
откуда  или
или 

 б)
б) 

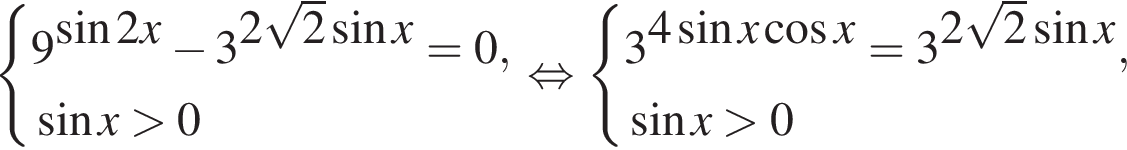
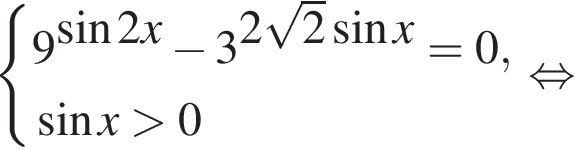




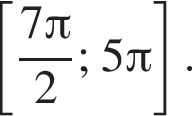 Получим число
Получим число  б)
б) 

 Сделаем замену
Сделаем замену  Получаем:
Получаем: 
 или
или 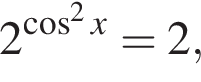 откуда
откуда  или
или 
 или
или  откуда
откуда  где
где  с помощью единичной окружности. Получаем
с помощью единичной окружности. Получаем  и
и  б)
б) 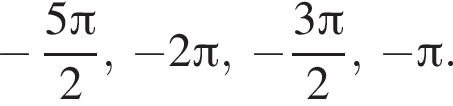
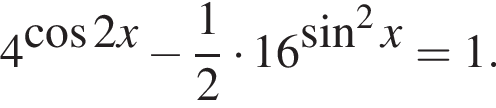





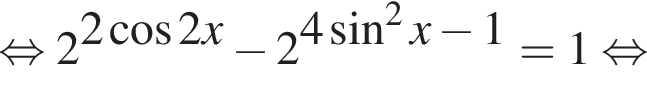
 тогда уравнение примет вид:
тогда уравнение примет вид:


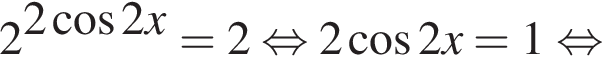


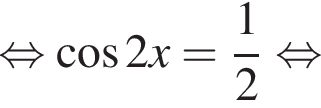



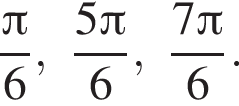
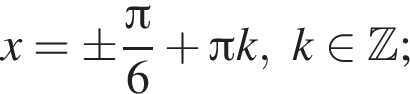 б)
б) 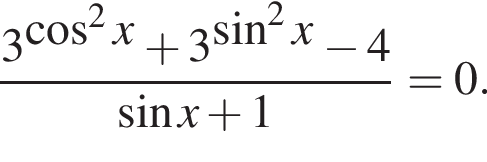













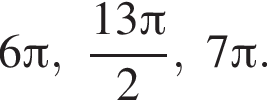
 б)
б) 








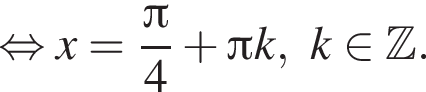




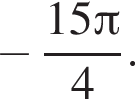
 б)
б) 

 тогда исходное уравнение примет вид:
тогда исходное уравнение примет вид:






 б)
б) 

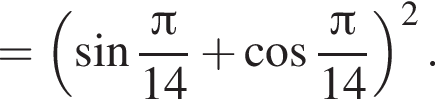
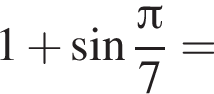



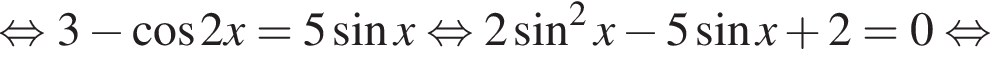
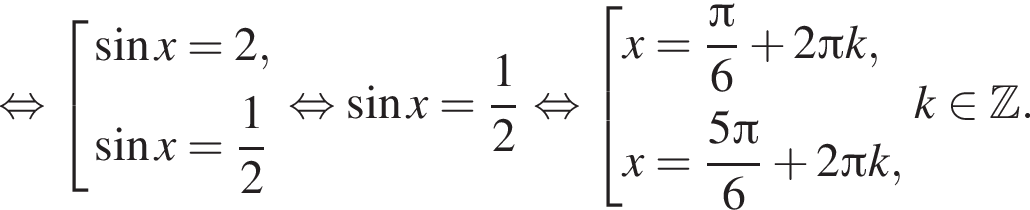






 с помощью тригонометрической окружности (см. рис.). Получаем:
с помощью тригонометрической окружности (см. рис.). Получаем:
 б)
б) 

 имеем:
имеем:



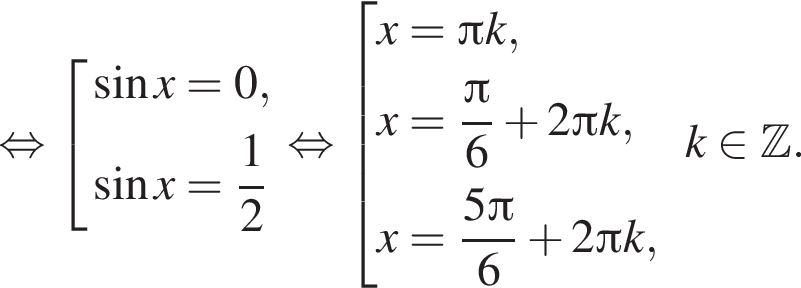

 с помощью тригонометрической окружности (см. рис.), получим
с помощью тригонометрической окружности (см. рис.), получим  б)
б) 

 и преобразуем уравнение:
и преобразуем уравнение: 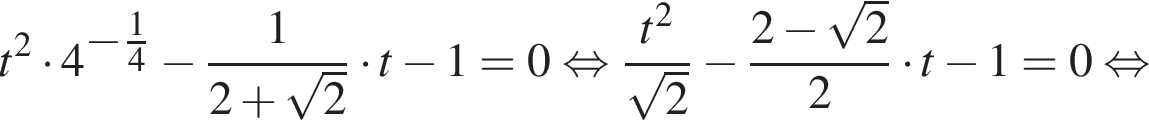






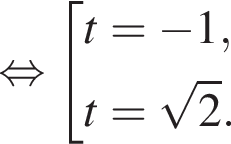





 отберём с помощью единичной окружности. Заметим, что
отберём с помощью единичной окружности. Заметим, что 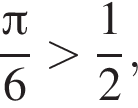 а
а  Подходит только корень
Подходит только корень  б)
б) 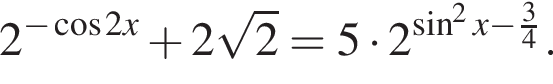



 имеем:
имеем: 







 б)
б) 
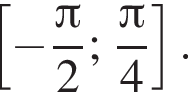




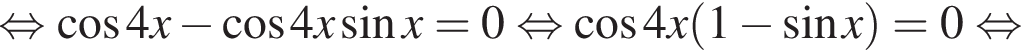







 б)
б) 


 Получаем:
Получаем:





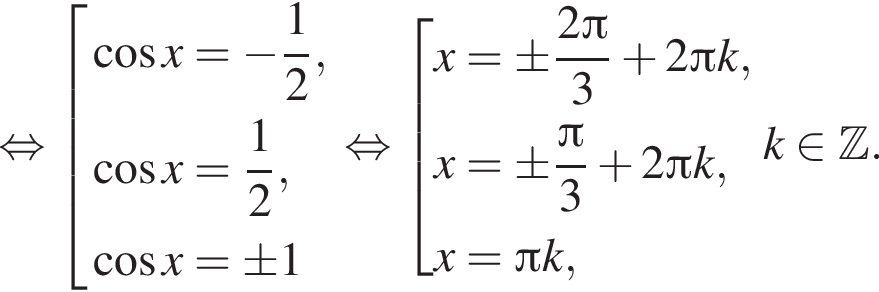




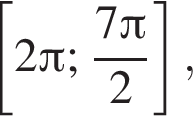 с помощью единичной окружности. Получаем
с помощью единичной окружности. Получаем  б)
б) 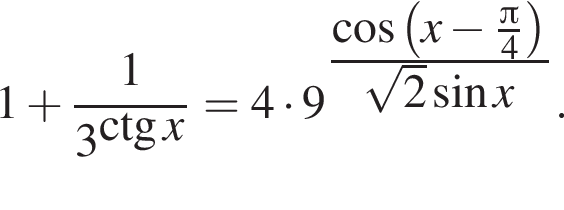

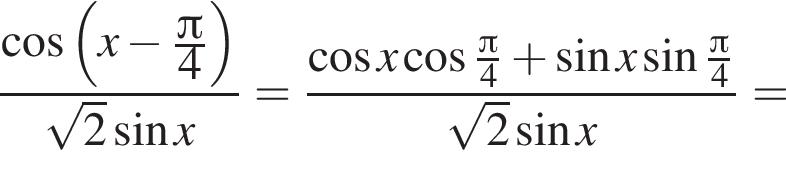




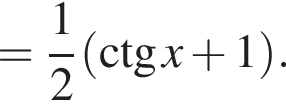

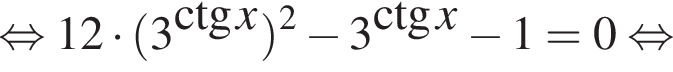



 б)
б) 

 получаем:
получаем:



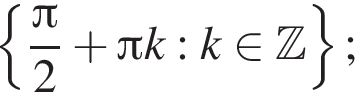 б)
б) 


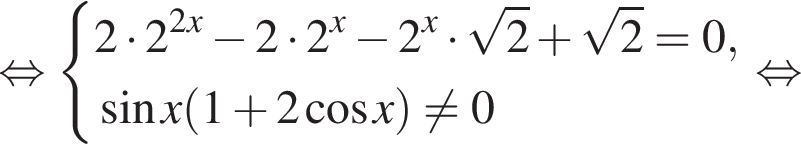
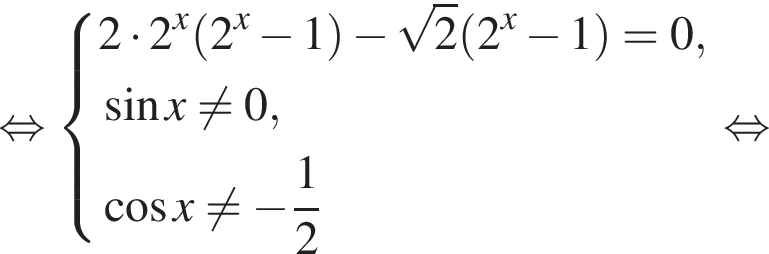





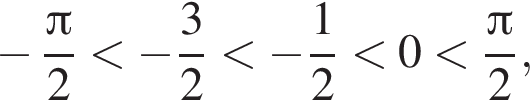 поэтому найденный корень лежит на заданном отрезке.
поэтому найденный корень лежит на заданном отрезке. б)
б) 








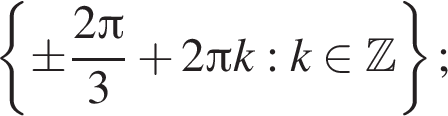 б)
б) 
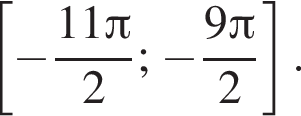
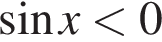 исходное уравнение эквивалентно уравнению:
исходное уравнение эквивалентно уравнению:









 б)
б) 









 б)
б) 

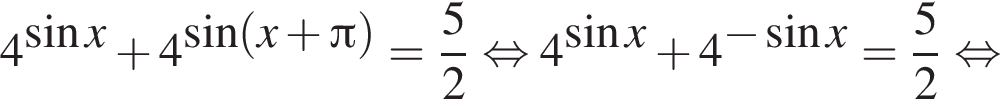









 Находим:
Находим:  б)
б) 

 тогда
тогда



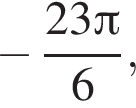
 б)
б) 



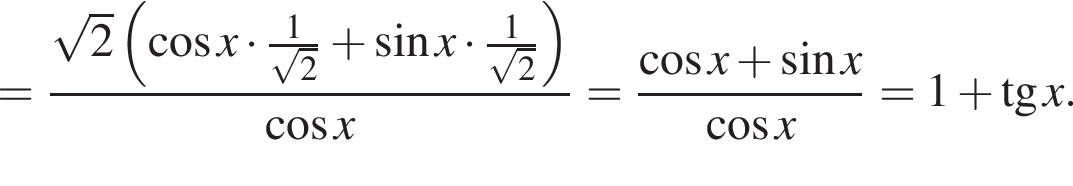





 получим:
получим:
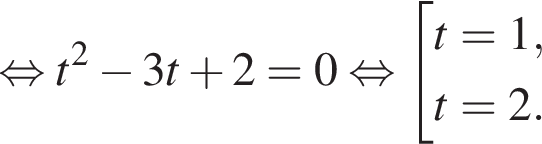






 б)
б) 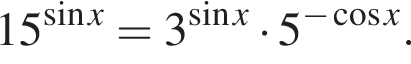
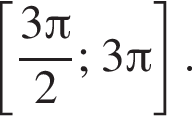




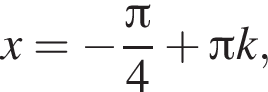
 Получим числа
Получим числа 
 б)
б) 







 и не больше одного члена серии
и не больше одного члена серии  Из первой серии это числа
Из первой серии это числа  б)
б) 


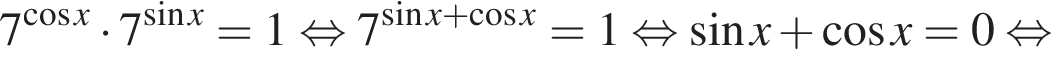



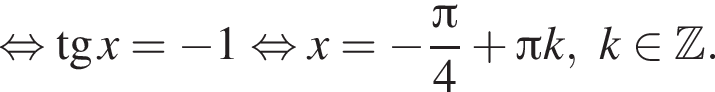





 :
:




 б)
б) 

 При этом условии оно равносильно совокупности:
При этом условии оно равносильно совокупности:






 Для второй серии аналогично:
Для второй серии аналогично:


 б)
б) 
 б)
б) 

 тогда:
тогда:





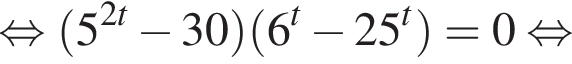





 не имеет решений. Осталось решить уравнение
не имеет решений. Осталось решить уравнение 
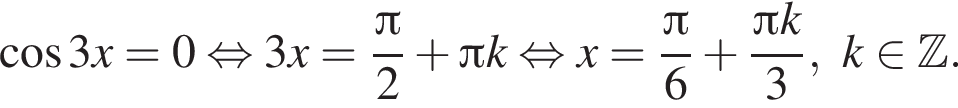


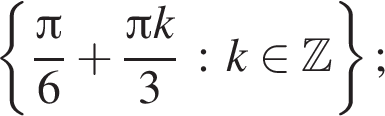 б)
б) 














 соответствуют решения
соответствуют решения  б)
б) 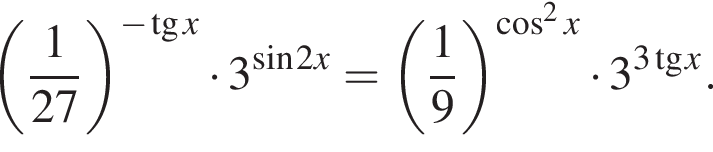






 Подходят число
Подходят число 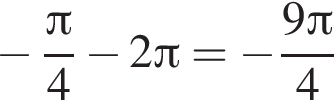 и число
и число 




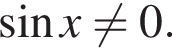 Получим:
Получим:












 отберем при помощи единичной окружности. Подходит число
отберем при помощи единичной окружности. Подходит число 

















 Тогда уравнение принимает вид
Тогда уравнение принимает вид
 получаем уравнение
получаем уравнение  оно не имеет решений. При
оно не имеет решений. При  получаем уравнение
получаем уравнение  Пусть
Пусть  тогда
тогда 
 или
или  Первое из этих уравнений не имеет решений, для второго уравнения находим:
Первое из этих уравнений не имеет решений, для второго уравнения находим:






 знаменатель не определен, а для всех чисел
знаменатель не определен, а для всех чисел  определен.
определен.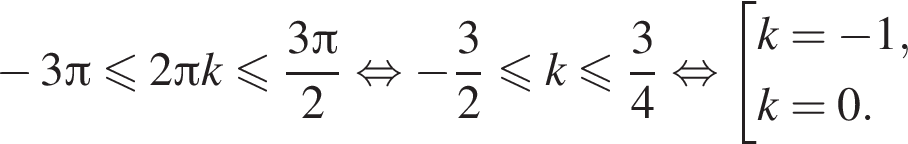



 Для таких значений x числитель дроби должен быть равен нулю:
Для таких значений x числитель дроби должен быть равен нулю:



 удовлетворяют числа
удовлетворяют числа 

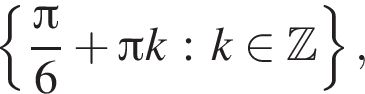 б)
б)