1. Тип 18 № 500004 

Классификатор алгебры: Уравнение окружности
Методы алгебры: Использование основного тригонометрического тождества и следствий из него
Задача с параметром. Уравнение окружности
i
Найдите все значения параметра a, при каждом из которых система  имеет ровно два решения.
имеет ровно два решения.
Решение. Неравенство задает пару вертикальных углов на координатной плоскости Oxy (см. рис.). Графиком уравнения является окружность радиуса
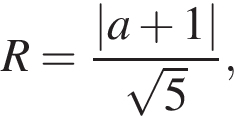 центр которой ― точка
центр которой ― точка  ― лежит на прямой
― лежит на прямой  Поскольку оба графика симметричны относительно прямой
Поскольку оба графика симметричны относительно прямой  система будет иметь ровно два решения тогда и только тогда, когда расстояние PK от центра окружности до прямой
система будет иметь ровно два решения тогда и только тогда, когда расстояние PK от центра окружности до прямой  будет равняться радиусу
будет равняться радиусу  данной окружности. Из треугольника POK находим:
данной окружности. Из треугольника POK находим:  где
где ![]() ― угловой коэффициент прямой
― угловой коэффициент прямой  Таким образом,
Таким образом, 
 откуда
откуда


![]()


![]()



Окончательно получаем:  или
или 
Ответ: ![]() или
или 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 4 |
| С помощью верного рассуждения получены искомые значения, возможно неверные, из-за одной допущенной вычислительной ошибки (описки) | 3 |
| С помощью верного рассуждения получено одно значение параметра (возможно неверное из-за одной вычислительной ошибки), а второе значение потеряно в результате ошибки (например «потеряны» модули) | 2 |
| Задача сведена к исследованию взаимного расположения графиков неравенства и уравнения (приведен правильный рисунок) | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
500004

Классификатор алгебры: Уравнение окружности


 задаёт на плоскости полосу, граница которой — пара параллельных прямых:
задаёт на плоскости полосу, граница которой — пара параллельных прямых:  и
и 
 то система не имеет решений, поскольку правая часть уравнения становится отрицательной. Если
то система не имеет решений, поскольку правая часть уравнения становится отрицательной. Если  то уравнение принимает вид:
то уравнение принимает вид:  и задаёт единственную точку
и задаёт единственную точку  координаты которой удовлетворяют неравенству:
координаты которой удовлетворяют неравенству:  Следовательно, при
Следовательно, при 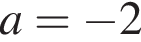 система имеет единственное решение.
система имеет единственное решение. Тогда уравнение
Тогда уравнение  определяет окружность радиусом
определяет окружность радиусом  Центр
Центр  окружности лежит на прямой y=2x, которая перпендикулярна граничным прямым полосы и пересекает их в точках
окружности лежит на прямой y=2x, которая перпендикулярна граничным прямым полосы и пересекает их в точках  и
и 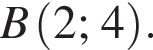 Система имеет единственное решение, если только окружность внешним образом касается полосы в точке A или в точке
Система имеет единственное решение, если только окружность внешним образом касается полосы в точке A или в точке  что невозможно. Окружность касается полосы в точке B, только если
что невозможно. Окружность касается полосы в точке B, только если  Получаем:
Получаем:















 и радиусом
и радиусом  Неравенство
Неравенство  определяет вертикальную полосу
определяет вертикальную полосу 


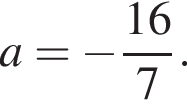 Вторая система имеет решение
Вторая система имеет решение 








 лежит на дуге ω2 и прямая OC перпендикулярна прямой O1O, поскольку произведение угловых коэффициентов данных прямых равно −1.
лежит на дуге ω2 и прямая OC перпендикулярна прямой O1O, поскольку произведение угловых коэффициентов данных прямых равно −1. прямая m проходит через точку C, значит, прямая m касается дуг ω2 и ω1, то есть исходная система имеет два решения.
прямая m проходит через точку C, значит, прямая m касается дуг ω2 и ω1, то есть исходная система имеет два решения. прямая m касается дуг ω2 и ω1, то есть исходная система имеет два решения.
прямая m касается дуг ω2 и ω1, то есть исходная система имеет два решения. или
или  прямая m пересекает каждую из дуг ω1 и ω2 в двух точках, отличных от точек A и B, то есть исходная система имеет четыре решения.
прямая m пересекает каждую из дуг ω1 и ω2 в двух точках, отличных от точек A и B, то есть исходная система имеет четыре решения. или
или  прямая m не пересекает дуги ω1 и ω2, то есть исходная система не имеет решений.
прямая m не пересекает дуги ω1 и ω2, то есть исходная система не имеет решений. или
или 


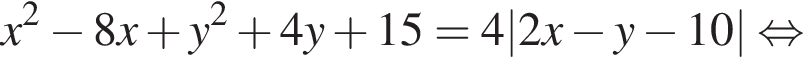



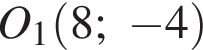 и
и  лежащих ниже и выше прямой
лежащих ниже и выше прямой 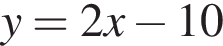 соответственно (см. рис.), пересекающихся в точках
соответственно (см. рис.), пересекающихся в точках  и
и  Заметим, что точка касания
Заметим, что точка касания  лежит на дуге
лежит на дуге  прямая m проходит через точку B и исходная система имеет три решения.
прямая m проходит через точку B и исходная система имеет три решения.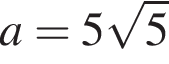 прямая m проходит через точку C, значит, прямая m касается дуг
прямая m проходит через точку C, значит, прямая m касается дуг  прямая m касается дуг
прямая m касается дуг  или
или  прямая m пересекает каждую из дуг
прямая m пересекает каждую из дуг  прямая m пересекает каждую из дуг
прямая m пересекает каждую из дуг 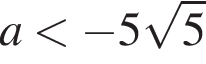 или
или  прямая m не пересекает дуги
прямая m не пересекает дуги  или
или 

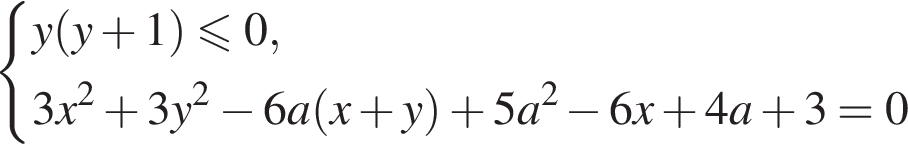



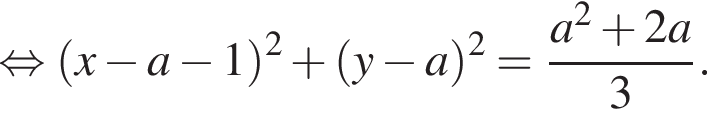
 и радиусом
и радиусом  Неравенство
Неравенство  определяет горизонтальную полосу
определяет горизонтальную полосу  На рисунке видно, что единственное решение получается в двух случаях.
На рисунке видно, что единственное решение получается в двух случаях. 






 а радиусы
а радиусы  и
и 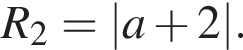 Решим два уравнения: (1)
Решим два уравнения: (1)  и (2)
и (2) 
 уравнение (2) имеет вид
уравнение (2) имеет вид  Решением уравнения (1) являются числа 1 и
Решением уравнения (1) являются числа 1 и 

 то получаем уравнение
то получаем уравнение


 и радиусом
и радиусом  то получаем уравнение
то получаем уравнение


 и радиусом
и радиусом  и
и  лежащих на прямой
лежащих на прямой  поэтому в первом случае получаем дугу
поэтому в первом случае получаем дугу  прямая m перпендикулярна прямой O1B, угловой коэффициент которой равен
прямая m перпендикулярна прямой O1B, угловой коэффициент которой равен  или
или 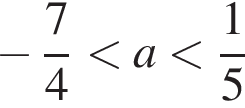 прямая m пересекает дугу
прямая m пересекает дугу  прямая m пересекает дугу
прямая m пересекает дугу 

 и радиусом 1,5. Второму уравнению — окружность с центром в точке
и радиусом 1,5. Второму уравнению — окружность с центром в точке  и радиусом
и радиусом  (возможно, эта окружность вырождается в точку, если
(возможно, эта окружность вырождается в точку, если  Тогда эта точка имеет координаты
Тогда эта точка имеет координаты  и на первой окружности не лежит). Система будет иметь единственное решение, если эти окружности касаются друг друга, то есть расстояние между их центрами будет равно сумме или разности радиусов.
и на первой окружности не лежит). Система будет иметь единственное решение, если эти окружности касаются друг друга, то есть расстояние между их центрами будет равно сумме или разности радиусов.  или
или 

 откуда
откуда 
 Последнее уравнение не имеет положительных корней.
Последнее уравнение не имеет положительных корней. эти уравнения превращаются соответственно в
эти уравнения превращаются соответственно в 
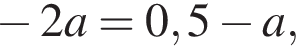
 откуда
откуда 
 Последнее уравнение не имеет корней на данном промежутке.
Последнее уравнение не имеет корней на данном промежутке. эти уравнения превращаются соответственно в
эти уравнения превращаются соответственно в 


 имеет единственное решение.
имеет единственное решение. задает окружность
задает окружность  радиуса
радиуса  того же радиуса (см. рис.).
того же радиуса (см. рис.). задаст окружность
задаст окружность 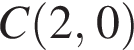 радиуса
радиуса  то
то 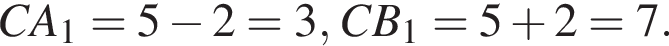
 или
или 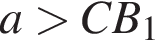 окружности
окружности  окружности
окружности  или
или  окружности
окружности  то
то 
 или
или  окружности
окружности  окружности
окружности  или
или  окружности
окружности  то условию задачи удовлетворяют только числа
то условию задачи удовлетворяют только числа 

 имеет ровно четыре решения.
имеет ровно четыре решения.


 получаем систему
получаем систему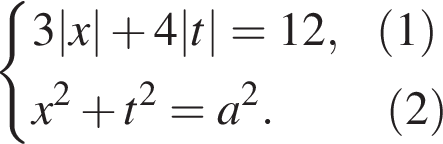
 (см. рис.).
(см. рис.).


 откуда
откуда  или
или 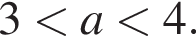

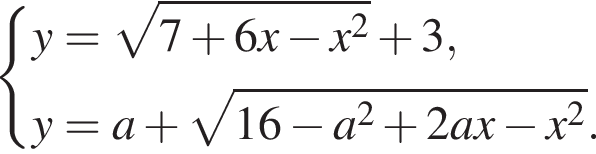






 являются искомыми.
являются искомыми. Поэтому искомое множество значений параметра а симметрично относительно точки a = 3, поэтому
Поэтому искомое множество значений параметра а симметрично относительно точки a = 3, поэтому 


 и
и  равносильны?
равносильны? равносильно бесконечной совокупности уравнений
равносильно бесконечной совокупности уравнений 
 соответствующей
соответствующей 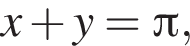 т. е. чем число
т. е. чем число 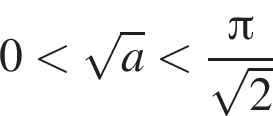 или
или  Добавляя полученные ранее значения
Добавляя полученные ранее значения 




 откуда
откуда 
 при остальных а решений нет.
при остальных а решений нет. не имеет решений.
не имеет решений.


 задает на координатной плоскости «верхнюю» полуплоскость с границей
задает на координатной плоскости «верхнюю» полуплоскость с границей 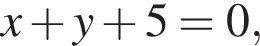 а уравнение
а уравнение  при
при  ― окружность с центром
― окружность с центром  и радиусом
и радиусом  (см. рис.).
(см. рис.). откуда
откуда 
 уравнение, а, следовательно, и вся система решений не имеют, а при
уравнение, а, следовательно, и вся система решений не имеют, а при  решением уравнения является пара
решением уравнения является пара  которая не удовлетворяет неравенству
которая не удовлетворяет неравенству 

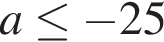


 Решения второго уравнения — точки прямой
Решения второго уравнения — точки прямой 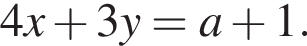 Следовательно, система имеет более одного решения тогда и только тогда, когда расстояние от центра окружности (3a − 1, −2a) до прямой
Следовательно, система имеет более одного решения тогда и только тогда, когда расстояние от центра окружности (3a − 1, −2a) до прямой  меньше радиуса
меньше радиуса  данной окружности. Получаем систему:
данной окружности. Получаем систему:


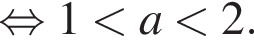


 то, раскрывая модуль, находим:
то, раскрывая модуль, находим:



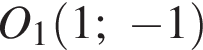 и радиусом 1.
и радиусом 1. то
то



 и радиусом
и радиусом  и
и  лежащих на окружности
лежащих на окружности  поэтому в первом случае получаем дугу
поэтому в первом случае получаем дугу  прямая m пересекает каждую из дуг
прямая m пересекает каждую из дуг  прямая m не пересекает дуги
прямая m не пересекает дуги 





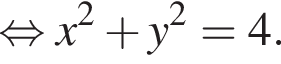
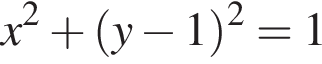 с концами в точках O и A(0; 2), во втором — прямую l, задаваемую уравнением x = 0, в третьем — дугу
с концами в точках O и A(0; 2), во втором — прямую l, задаваемую уравнением x = 0, в третьем — дугу  с концами в точках A и B(0; −2) (см. рис.).
с концами в точках A и B(0; −2) (см. рис.).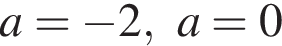 и
и  и
и  прямые m касаются дуг
прямые m касаются дуг  имеет две общие точки с дугой
имеет две общие точки с дугой  имеет одну общую точку с дугой
имеет одну общую точку с дугой  и
и  имеет две общие точки с дугой
имеет две общие точки с дугой 



 возможно, с включением граничных точек
возможно, с включением граничных точек









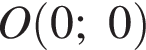 и радиусом 1.
и радиусом 1. во втором — прямую l, задаваемую уравнением
во втором — прямую l, задаваемую уравнением  с концами в точках A и
с концами в точках A и  (см. рис.).
(см. рис.). и
и  и
и  прямые m касаются дуги
прямые m касаются дуги  имеет одну общую точку с дугой
имеет одну общую точку с дугой 
 и
и  имеет две общие точки с дугой
имеет две общие точки с дугой  и
и 
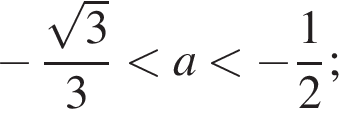

 множества значений a, возможно, с включением граничных точек
множества значений a, возможно, с включением граничных точек
 задает прямую. Эта прямая при всех a проходит через точку
задает прямую. Эта прямая при всех a проходит через точку 

 и радиусом
и радиусом  Система не будет иметь решений тогда и только тогда, когда прямая
Система не будет иметь решений тогда и только тогда, когда прямая  проведёнными из точки
проведёнными из точки  Значит, для касательных к окружности
Значит, для касательных к окружности 

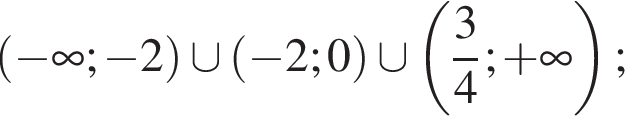


 имеем два случая:
имеем два случая:  (1) или
(1) или  (2)
(2) 

 система имеет два решения. Оба они лежат в области
система имеет два решения. Оба они лежат в области  исходная система уравнений имеет ровно два решения.
исходная система уравнений имеет ровно два решения.

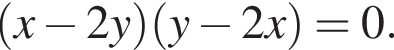 Следовательно, уравнение задает пару прямых
Следовательно, уравнение задает пару прямых 




 проводится к
проводится к  при условии
при условии  и задает верхнюю полуокружность радиуса
и задает верхнюю полуокружность радиуса 
 приводится к
приводится к  при условии
при условии  и задает верхнюю полуокружность радиуса
и задает верхнюю полуокружность радиуса  Ее центр перемещается по прямой
Ее центр перемещается по прямой 

 имеем:
имеем:



 имеем:
имеем:

 и радиусом 5.
и радиусом 5. и
и  лежащих на окружности
лежащих на окружности  поэтому в первом случае получаем два луча l1 и l2 с концами в точках A и B соответсвенно, во втором — дугу
поэтому в первом случае получаем два луча l1 и l2 с концами в точках A и B соответсвенно, во втором — дугу  лежит на дуге
лежит на дуге  прямая m проходит через точку C, значит, прямая m касается дуги
прямая m проходит через точку C, значит, прямая m касается дуги  прямая m пересекает дугу
прямая m пересекает дугу  или
или  прямая m не имеет общих точек с лучами l1 и l2 и дугой
прямая m не имеет общих точек с лучами l1 и l2 и дугой 
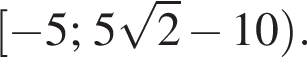


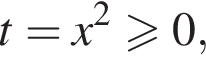 тогда из исходной системы получим
тогда из исходной системы получим



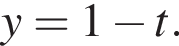 Уравнение
Уравнение  при
при  означает, что решения системы (⁎) должны лежать строго выше прямой
означает, что решения системы (⁎) должны лежать строго выше прямой 
 Пусть
Пусть  Эта точка имеет координаты
Эта точка имеет координаты 

 Получаем:
Получаем: 
 Имеем:
Имеем:  откуда
откуда 


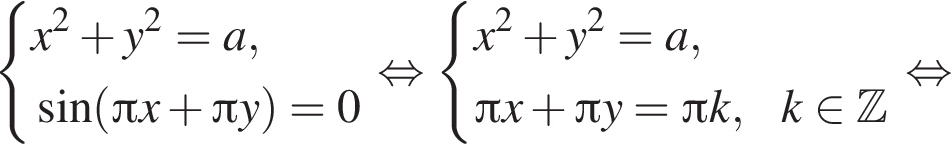

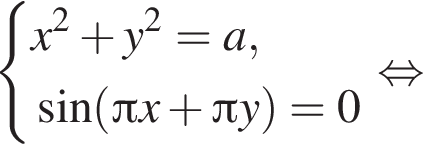

 при любом значении
при любом значении  и прямая
и прямая  касаются окружности при одном и том же значении a. Радиус окружности в этом случае равен половине диагонали квадрата со стороной 1, то есть радиус равен
касаются окружности при одном и том же значении a. Радиус окружности в этом случае равен половине диагонали квадрата со стороной 1, то есть радиус равен Значит, при
Значит, при 

 то каждое уравнение системы есть уравнение окружности. В этом случае система имеет единственное решение тогда и только тогда, когда расстояние между центрами этих окружностей равно сумме или разности их радиусов. При
то каждое уравнение системы есть уравнение окружности. В этом случае система имеет единственное решение тогда и только тогда, когда расстояние между центрами этих окружностей равно сумме или разности их радиусов. При  имеем систему
имеем систему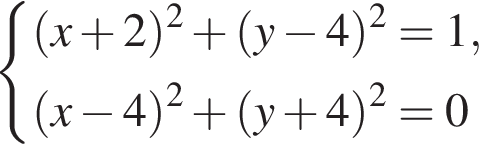
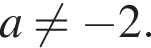 Расстояние O1O2 между центрами
Расстояние O1O2 между центрами  и
и  равно
равно и
и  Уравнение (1) имеет вид
Уравнение (1) имеет вид  уравнение (2) имеет вид
уравнение (2) имеет вид 
 Поэтому неравенство задаёт пару вертикальных углов в плоскости Oax. Уравнение
Поэтому неравенство задаёт пару вертикальных углов в плоскости Oax. Уравнение  задаёт окружность с центром (0; 0) радиуса 4 в этой же плоскости. Решения системы — точки дуг окружности, лежащие в указанных вертикальных углах.
задаёт окружность с центром (0; 0) радиуса 4 в этой же плоскости. Решения системы — точки дуг окружности, лежащие в указанных вертикальных углах.  и
и 






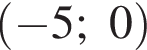 с угловым коэффициентом
с угловым коэффициентом  (см. рис., выделено синим). Графиком второго уравнения является семейство окружностей с центром в точке
(см. рис., выделено синим). Графиком второго уравнения является семейство окружностей с центром в точке  где a1 — абсцисса центра окружности, касающейся ломаной; a2 — абсцисса центра окружности, проходящей через точку
где a1 — абсцисса центра окружности, касающейся ломаной; a2 — абсцисса центра окружности, проходящей через точку  Найдём a1, используя формулу расстояния от точки до прямой. Расстояние от точки
Найдём a1, используя формулу расстояния от точки до прямой. Расстояние от точки 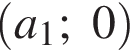 до прямой
до прямой  должно равняться радиусу окружности:
должно равняться радиусу окружности: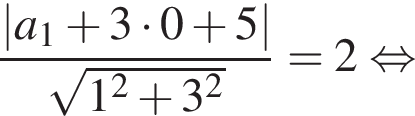


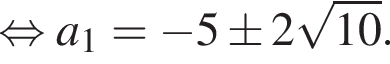
 поэтому
поэтому 












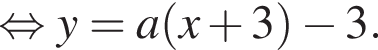


 и радиусом
и радиусом  и прямой
и прямой  Соответствующие две дуги окружности выделены на рисунке синим цветом. Графиком второго уравнения исходной системы является пучок прямых, проходящих через точку
Соответствующие две дуги окружности выделены на рисунке синим цветом. Графиком второго уравнения исходной системы является пучок прямых, проходящих через точку 
 или
или  или
или 
 проходящей через точку
проходящей через точку  (выделено оранжевым),
(выделено оранжевым),  (выделено зелёным),
(выделено зелёным), 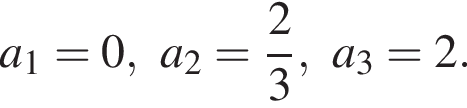 Найдём
Найдём  должно равняться
должно равняться 







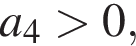 поэтому
поэтому  Отметим также, что
Отметим также, что  значит, исходная система имеет ровно одно решение при
значит, исходная система имеет ровно одно решение при  или
или 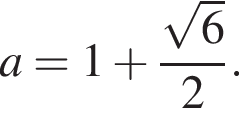

 имеет два решения при
имеет два решения при  или при
или при 
 имеет единственное решение на отрезке [−1;1]
имеет единственное решение на отрезке [−1;1] или
или 
 Оно имеет единственное решение x = 1 на отрезке [−1;1] при
Оно имеет единственное решение x = 1 на отрезке [−1;1] при  Эта система имеет единственное решение
Эта система имеет единственное решение  на отрезке [−1;1] при
на отрезке [−1;1] при  и не имеет решение на этом промежутке при других значениях параметра а.
и не имеет решение на этом промежутке при других значениях параметра а. 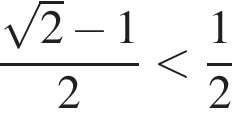 уравнение
уравнение 
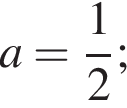

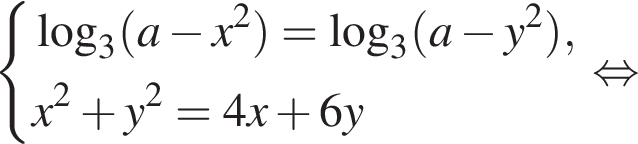



 задают две прямые, проходящие через начало координат. Двойное неравенство
задают две прямые, проходящие через начало координат. Двойное неравенство  задают внутреннюю часть вертикальной полосы, ограниченной прямыми
задают внутреннюю часть вертикальной полосы, ограниченной прямыми 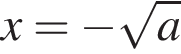 и
и  Уравнение
Уравнение  задает окружность с центром в точке
задает окружность с центром в точке  то есть
то есть  откуда
откуда 
 которые могут быть решениями системы при условии существования логарифмов. Требуется, чтобы (строго) внутрь полосы
которые могут быть решениями системы при условии существования логарифмов. Требуется, чтобы (строго) внутрь полосы  симметричной относительно оси ординат, попали ровно две из трех этих точек. Это происходит в точности тогда, когда
симметричной относительно оси ординат, попали ровно две из трех этих точек. Это происходит в точности тогда, когда  Таким образом,
Таким образом, 



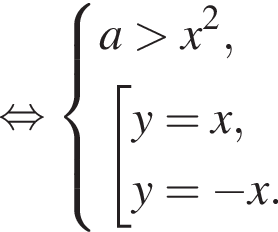
 принимает вид:
принимает вид:  Подставляя в полученное уравнение y = x, получаем
Подставляя в полученное уравнение y = x, получаем  откуда
откуда 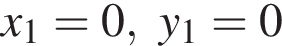 или
или  Подставляя в уравнение (⁎)
Подставляя в уравнение (⁎) 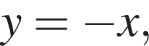 получаем
получаем  откуда
откуда  или
или 
 или
или  или
или 





 задаёт пучок прямых, проходящих через начало координат, симметричных друг другу относительно оси ординат и совпадающих при
задаёт пучок прямых, проходящих через начало координат, симметричных друг другу относительно оси ординат и совпадающих при  задает горизонтальную полосу, ограниченную прямыми
задает горизонтальную полосу, ограниченную прямыми  и
и  задает окружность с центром в точке
задает окружность с центром в точке  имеют с этой дугой окружности ровно две общие точки.
имеют с этой дугой окружности ровно две общие точки.  Касательная к окружности перпендикулярна радиусу, проведенному в точку касания, то есть перпендикулярна прямой
Касательная к окружности перпендикулярна радиусу, проведенному в точку касания, то есть перпендикулярна прямой  содержащий этот радиус (см. рис.). Две прямые на плоскости, отличные от координатных осей, перпендикулярны тогда и только тогда, когда произведение их угловых коэффициентов равно −1. Тем самым
содержащий этот радиус (см. рис.). Две прямые на плоскости, отличные от координатных осей, перпендикулярны тогда и только тогда, когда произведение их угловых коэффициентов равно −1. Тем самым  откуда
откуда  Следовательно, искомое уравнение касательной есть
Следовательно, искомое уравнение касательной есть  что соответствует значениям
что соответствует значениям  При этом вторая прямая
При этом вторая прямая  не пересекает дугу окружности в точке, отличной от начала координат, а значит, найденные значения параметра не являются искомыми.
не пересекает дугу окружности в точке, отличной от начала координат, а значит, найденные значения параметра не являются искомыми. или при
или при  за исключением ранее отброшенных точек
за исключением ранее отброшенных точек 


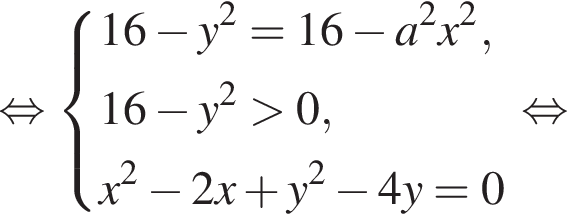


 задает внутреннюю часть горизонтальной полосы, ограниченной прямыми
задает внутреннюю часть горизонтальной полосы, ограниченной прямыми  задает окружность с центром в точке
задает окружность с центром в точке  одинаково. Поэтому искомые значения параметра симметричны относительно нуля. Рассмотрим случай
одинаково. Поэтому искомые значения параметра симметричны относительно нуля. Рассмотрим случай  если при этом прямая
если при этом прямая  не пересекает дугу в точке, отличной от точки
не пересекает дугу в точке, отличной от точки  содержащий этот радиус (см. рис.). Две прямые на плоскости, отличные от координатных осей, перпендикулярны тогда и только тогда, когда произведение их угловых коэффициентов равно −1. Тем самым
содержащий этот радиус (см. рис.). Две прямые на плоскости, отличные от координатных осей, перпендикулярны тогда и только тогда, когда произведение их угловых коэффициентов равно −1. Тем самым  откуда
откуда  Следовательно, искомое уравнение касательной есть
Следовательно, искомое уравнение касательной есть  что соответствует значениям
что соответствует значениям  пересекает дугу в точке, отличной от начала координат, а значит, найденное значение параметра является искомым.
пересекает дугу в точке, отличной от начала координат, а значит, найденное значение параметра является искомым.



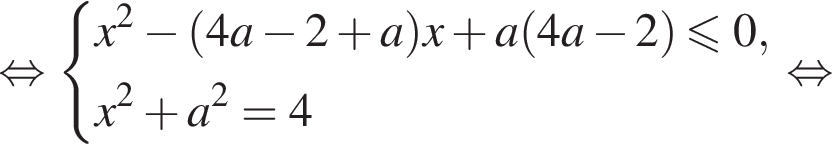
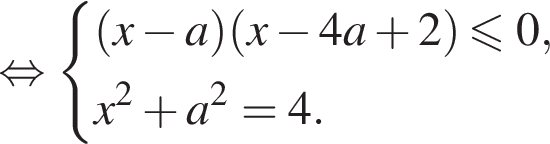
 в плоскости
в плоскости  разбивают плоскость на четыре области, обозначенных римскими цифрами. В каждой из областей левая часть исходного неравенства сохраняет знак. Установим, в каких областях неравенство верно, взяв пробные точки.
разбивают плоскость на четыре области, обозначенных римскими цифрами. В каждой из областей левая часть исходного неравенства сохраняет знак. Установим, в каких областях неравенство верно, взяв пробные точки.
 — верно.
— верно.
 — неверно.
— неверно.
 — верно.
— верно.
 — неверно.
— неверно.  является окружность с центром в точке
является окружность с центром в точке  лежащие внутри области, являющейся решением неравенства
лежащие внутри области, являющейся решением неравенства  Эти дуги выделены на рисунке цветом травы.
Эти дуги выделены на рисунке цветом травы.






 или при
или при 





 и радиусом
и радиусом  определяет горизонтальную полосу
определяет горизонтальную полосу 
 или
или 
 или
или 
 откуда
откуда 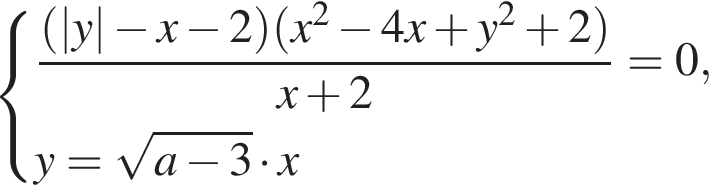
 значит,
значит, 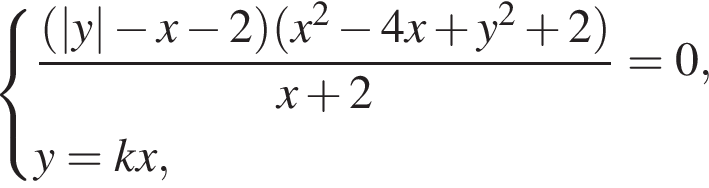
 задаваемой уравнением
задаваемой уравнением 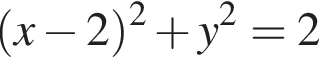 и двух лучей, задаваемых уравнением
и двух лучей, задаваемых уравнением  за исключением точки
за исключением точки 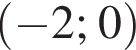 График второго уравнения представляет собой пучок прямых, проходящих через начало координат, с неотрицательным угловым коэффициентом.
График второго уравнения представляет собой пучок прямых, проходящих через начало координат, с неотрицательным угловым коэффициентом. прямая
прямая  то есть имеются две общие точки. При
то есть имеются две общие точки. При 


 и
и  Последнее означает, что центр окружности принадлежит гиперболе
Последнее означает, что центр окружности принадлежит гиперболе 
 Отсюда находим:
Отсюда находим:






 лежащих ниже и выше прямой
лежащих ниже и выше прямой  соответственно (см. рис.), пересекающихся в точках
соответственно (см. рис.), пересекающихся в точках  и
и  Количество корней равнения равно количеству точек пересечения графика уравнения с горизонтальной прямой при соответствующем значении a.
Количество корней равнения равно количеству точек пересечения графика уравнения с горизонтальной прямой при соответствующем значении a.  уравнение не имеет корней;
уравнение не имеет корней; уравнение имеет один корень;
уравнение имеет один корень; уравнение имеет два корня;
уравнение имеет два корня; уравнение имеет три корня;
уравнение имеет три корня; уравнение имеет четыре корня;
уравнение имеет четыре корня; уравнение имеет два корня;
уравнение имеет два корня; уравнение имеет четыре корня;
уравнение имеет четыре корня; уравнение имеет три корня;
уравнение имеет три корня; уравнение имеет два корня;
уравнение имеет два корня; уравнение имеет один корень;
уравнение имеет один корень; уравнение не имеет корней.
уравнение не имеет корней. при
при 


 уравнение
уравнение  не имеет корней, поскольку его левая часть принимает неотрицательные значения, а правая — отрицательные.
не имеет корней, поскольку его левая часть принимает неотрицательные значения, а правая — отрицательные.  уравнение
уравнение  и
и 
 уравнение
уравнение  принимает вид:
принимает вид: 


 с концами в точках (0; 0) и (1; −1).
с концами в точках (0; 0) и (1; −1).  принимает вид:
принимает вид: 


 и
и  в одной точке при
в одной точке при 
 и
и  и
и 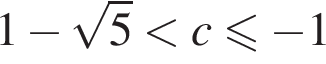 и
и  в одной точке при
в одной точке при 
 и не пересекается при
и не пересекается при  и
и 
 и при
и при  и
и 

 но неверно определены промежутки значений a
но неверно определены промежутки значений a 


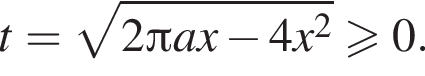 Решим уравнение:
Решим уравнение:

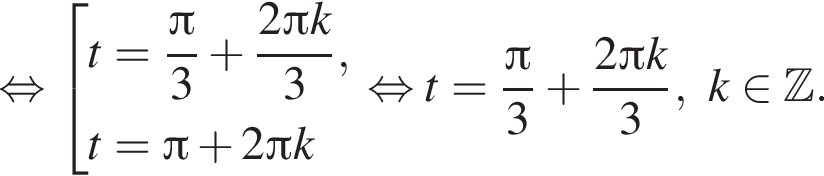







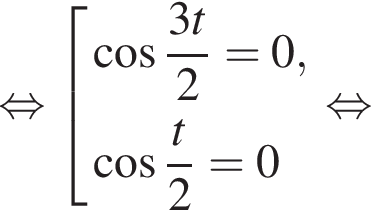


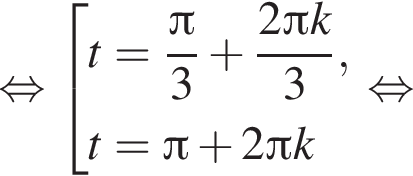






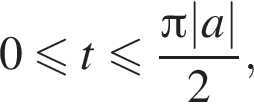 причём каждому такому t, кроме
причём каждому такому t, кроме  соответствуют два различных значения x.
соответствуют два различных значения x.
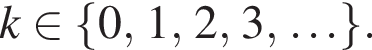 При
При  и
и 




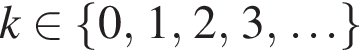 представляет собой совокупность горизонтальных прямых. При
представляет собой совокупность горизонтальных прямых. При  то есть при
то есть при 










 делят плоскость на четыре части. Неравенству системы соответствует множество точек, отмеченных на рисунке салатовым цветом. Прямая
делят плоскость на четыре части. Неравенству системы соответствует множество точек, отмеченных на рисунке салатовым цветом. Прямая  пересекает окружность в точках
пересекает окружность в точках  и
и  Прямая
Прямая  и
и  где
где 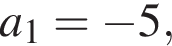
 Таким образом, графиком системы являются две дуги указанной окружности — дуга AB и дуга CD (выделено оранжевым).
Таким образом, графиком системы являются две дуги указанной окружности — дуга AB и дуга CD (выделено оранжевым). и
и  то есть при
то есть при 
 и
и 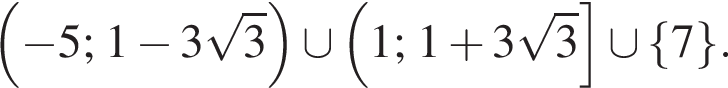
 исходное уравнение имеет два различных решения, а при других значениях параметра решений нет.
исходное уравнение имеет два различных решения, а при других значениях параметра решений нет. имеет ровно два корня на
имеет ровно два корня на 

 тогда
тогда
 пересекающих ось ординат в точке
пересекающих ось ординат в точке 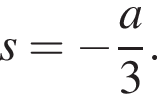 В силу введённых обозначений справедливо равенство
В силу введённых обозначений справедливо равенство  задающее в системе координат sOt единичную окружность с центром в точке О.
задающее в системе координат sOt единичную окружность с центром в точке О. следует, что
следует, что  Поэтому искомыми являются те значения параметра, при которых прямые, задаваемые уравнением (⁎), имеют с единичной окружностью (⁎⁎) две точки пересечения, на дуге, для которой
Поэтому искомыми являются те значения параметра, при которых прямые, задаваемые уравнением (⁎), имеют с единичной окружностью (⁎⁎) две точки пересечения, на дуге, для которой 
 (выделено зелёным) координаты точки
(выделено зелёным) координаты точки 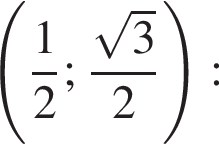

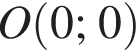 и прямой
и прямой  получаем:
получаем:
 получаем:
получаем:



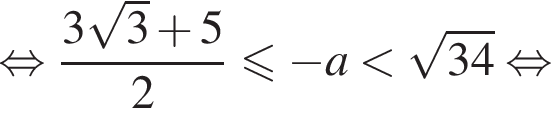







 задает окружность с центром в точке (3; −2) и радиусом
задает окружность с центром в точке (3; −2) и радиусом  В силу тождества
В силу тождества  окружность проходит через начало координат. Уравнение
окружность проходит через начало координат. Уравнение 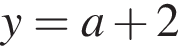 задает прямые, параллельные оси абсцисс. Поскольку x > 0, система имеет ровно два различных решения тогда и только тогда, когда эти прямые имеют в правой относительно оси ординат полуплоскости ровно две точки пересечения с окружностью (см. рис.).
задает прямые, параллельные оси абсцисс. Поскольку x > 0, система имеет ровно два различных решения тогда и только тогда, когда эти прямые имеют в правой относительно оси ординат полуплоскости ровно две точки пересечения с окружностью (см. рис.). 









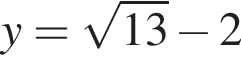








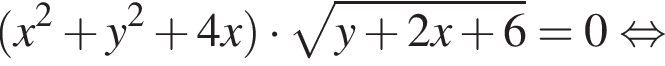




 и дуги окружности радиуса 2 с центром в точке
и дуги окружности радиуса 2 с центром в точке 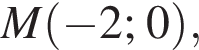 лежащей не ниже прямой
лежащей не ниже прямой  является пучок прямых, проходящих через точку
является пучок прямых, проходящих через точку 
 и прямая
и прямая  и
и 
 имеет одно решение;
имеет одно решение; имеет одно решение;
имеет одно решение; — три решения;
— три решения; — два решения;
— два решения; — три решения;
— три решения;





 или
или 



 Снимая на этом промежутке знаки модулей, находим:
Снимая на этом промежутке знаки модулей, находим:



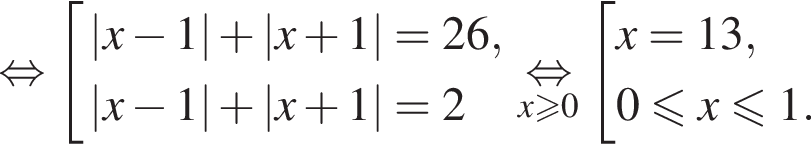


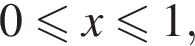 тогда первое уравнение системы принимает вид
тогда первое уравнение системы принимает вид  откуда
откуда 
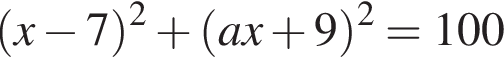 должно иметь ровно один корень. Запишем его в виде
должно иметь ровно один корень. Запишем его в виде







 При
При 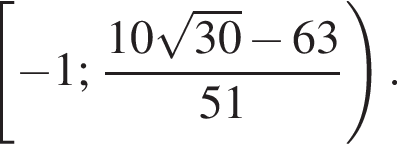









 а ветви параболы
а ветви параболы  направлены вниз, следовательно, хотя бы одно решение будет, если
направлены вниз, следовательно, хотя бы одно решение будет, если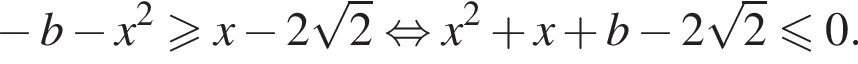


 откуда:
откуда: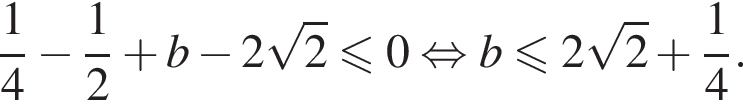

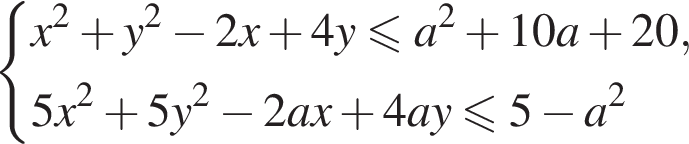



 вырождается в точку. Чтобы система имела хотя бы одно решение расстояние между центрами кругов должно быть не больше суммы их радиусов:
вырождается в точку. Чтобы система имела хотя бы одно решение расстояние между центрами кругов должно быть не больше суммы их радиусов:






 имеем:
имеем:







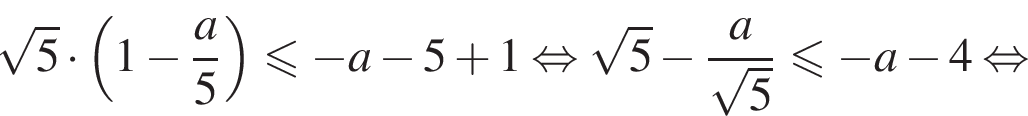







 или
или 

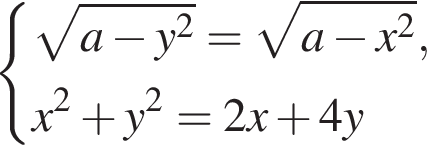





 при отрицательных значениях параметра a не имеет решений, при
при отрицательных значениях параметра a не имеет решений, при  и
и 

 система имеет ровно одно решение;
система имеет ровно одно решение; система имеет ровно два решения;
система имеет ровно два решения;