1. Тип 15 № 505567 

Классификатор алгебры: Модуль числа, Неравенства с логарифмами по переменному основанию
Методы алгебры: Метод интервалов
Кодификатор ФИПИ/Решу ЕГЭ: 2.2.9 Метод интервалов
Неравенства. Неравенства с логарифмами по переменному основанию
i
Решите неравенство: 
Решение. Областью определения неравенства являются положительные числа, отличные от 0,25 и 1. Выражение  либо равно нулю при
либо равно нулю при ![]() при этом неравенство верно; либо положительно, и тогда на него можно разделить, не меняя знака неравенства. Имеем:
при этом неравенство верно; либо положительно, и тогда на него можно разделить, не меняя знака неравенства. Имеем:




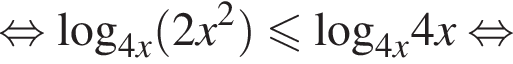



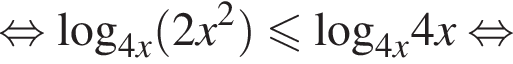

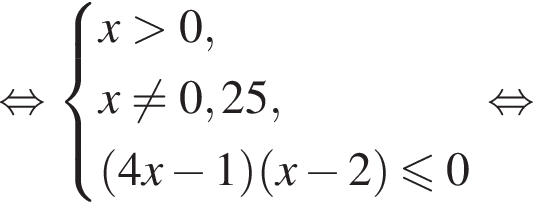

Учитывая, что ![]() получаем ответ:
получаем ответ: 
Ответ: 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 2 |
| Обоснованно получен ответ, отличающийся от верного исключением точек, ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Ответ: 

505567

Классификатор алгебры: Модуль числа, Неравенства с логарифмами по переменному основанию
Методы алгебры: Метод интервалов
Кодификатор ФИПИ/Решу ЕГЭ: 2.2.9 Метод интервалов

 и
и  то есть при
то есть при  и
и 


 тогда
тогда 
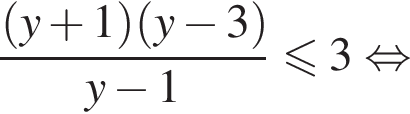

 или
или  Из полученного набора нужно ещё исключить
Из полученного набора нужно ещё исключить 

 тогда неравенство принимает вид
тогда неравенство принимает вид 









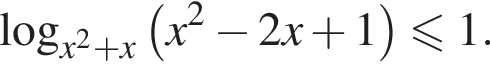
 то
то


 или
или  то
то


 или
или 
 или
или 



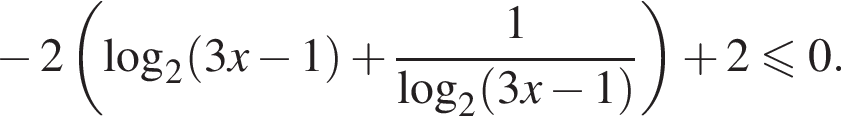

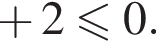
 тогда
тогда  и, следовательно,
и, следовательно, 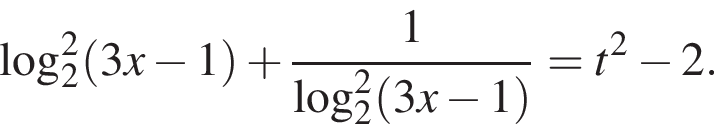
 откуда
откуда 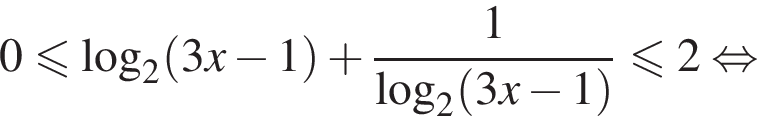









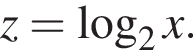





 или
или  откуда находим решение неравенства:
откуда находим решение неравенства: 





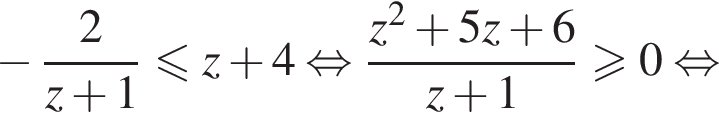



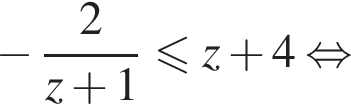





 и
и  неравенство равносильно неравенству:
неравенство равносильно неравенству: 
 получаем:
получаем: 


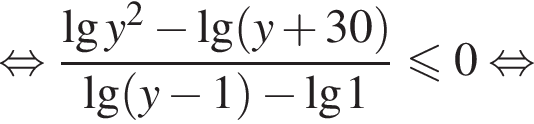









 получаем множество решений неравенства:
получаем множество решений неравенства: 
 можно произвести следующие преобразования:
можно произвести следующие преобразования:














 Полученные значения переменной удовлетворяют условию
Полученные значения переменной удовлетворяют условию 
 Имеем:
Имеем:







 получаем:
получаем:  Решение неравенства:
Решение неравенства: 

















 Рассмотрим два случая.
Рассмотрим два случая.  Получаем, что
Получаем, что  Тогда
Тогда




 следовательно, при
следовательно, при  исходное неравенство верно.
исходное неравенство верно.

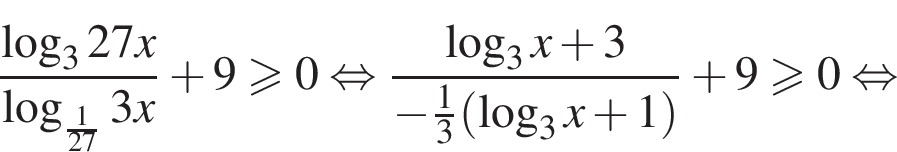





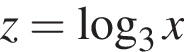 :
:
 или
или  откуда
откуда  или
или 






 получаем:
получаем:  или
или 
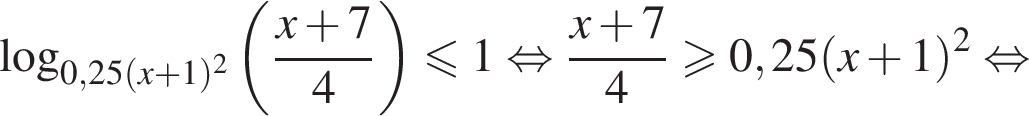



 получаем:
получаем: 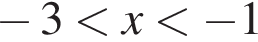 или
или 



 и
и  а значит,
а значит,  и
и 



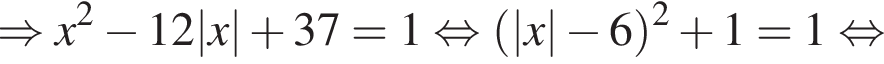








 тогда неравенство примет вид:
тогда неравенство примет вид: 





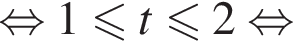


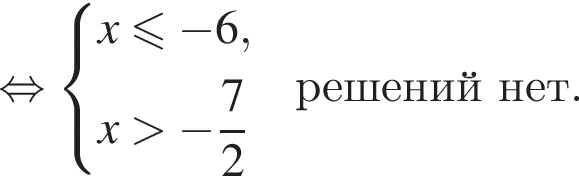




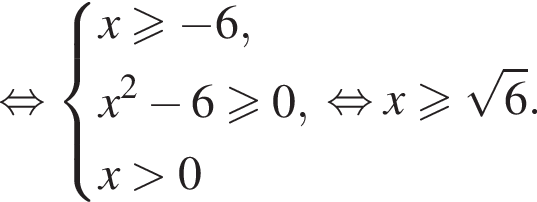






 Получаем:
Получаем: 
 Тогда
Тогда



 Первое неравенство верно при
Первое неравенство верно при  При
При  больше 1, а значит, левая часть исходного неравенства положительна. Тогда положительна и правая часть, откуда
больше 1, а значит, левая часть исходного неравенства положительна. Тогда положительна и правая часть, откуда  имеем:
имеем:



 то
то  и
и 

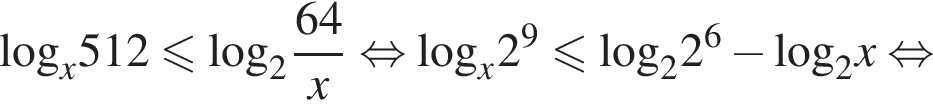





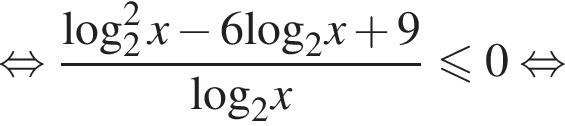









 Пусть
Пусть 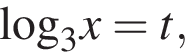 тогда
тогда





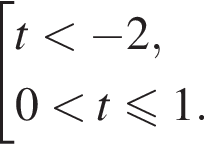 Теперь перейдем к переменной x.
Теперь перейдем к переменной x.





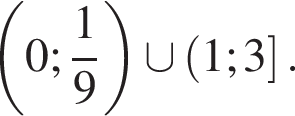







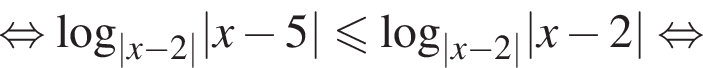





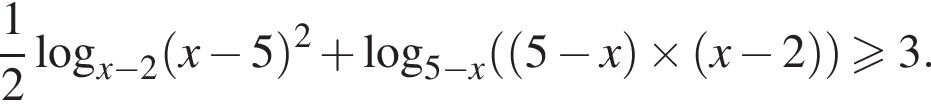

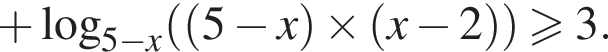



 Получаем
Получаем  откуда z > 0. Обратная замена:
откуда z > 0. Обратная замена:









 тогда
тогда  Решим неравенство методом интервалов:
Решим неравенство методом интервалов: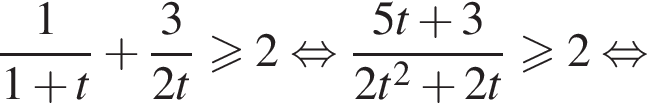










 и обращается в ноль только при
и обращается в ноль только при  то есть и
то есть и  при
при 
 при
при 

 и
и  при
при  то есть
то есть  при
при 
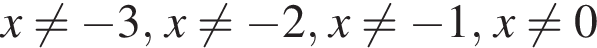 имеем:
имеем:





 или
или 






 :
: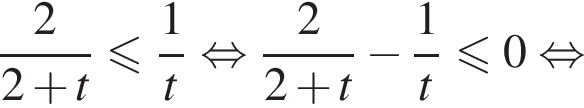












 и приведем левую часть к общему знаменателю:
и приведем левую часть к общему знаменателю:


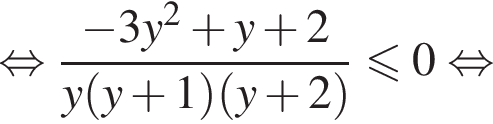

 Возвращаясь к переменной x, находим множество решений исходного неравенства:
Возвращаясь к переменной x, находим множество решений исходного неравенства: 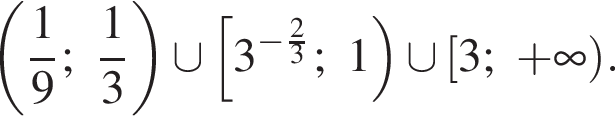


 откуда получаем
откуда получаем  и данное неравенство равносильно неравенству
и данное неравенство равносильно неравенству

 где
где  Заметим, что при
Заметим, что при  возрастает (произведение двух положительных возрастающих функций) и
возрастает (произведение двух положительных возрастающих функций) и  Таким образом, множеством решений этого неравенства является луч
Таким образом, множеством решений этого неравенства является луч 








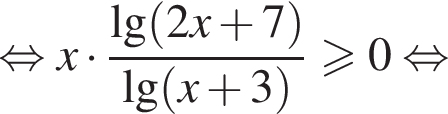










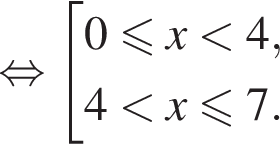

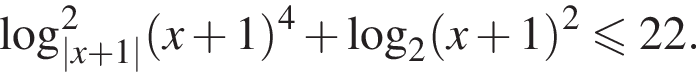
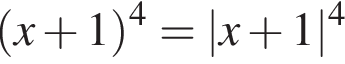 и что
и что 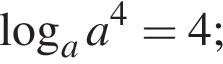 поэтому первое слагаемое равно 42 = 16. Имеем:
поэтому первое слагаемое равно 42 = 16. Имеем:









 получаем
получаем 








 решим неравенство
решим неравенство  Используя свойство логарифма
Используя свойство логарифма  перейдём к основанию 2, получим:
перейдём к основанию 2, получим:
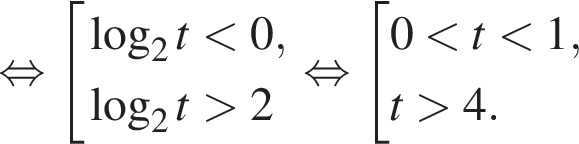








 имеем:
имеем:



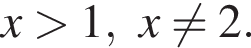
 получаем:
получаем: 





 Заметим, что
Заметим, что 

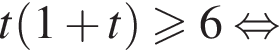












 тогда
тогда 












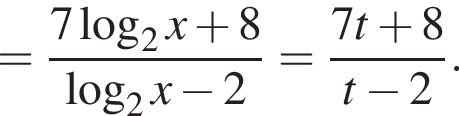






 то есть при
то есть при  запишем исходное неравенство в упрощенном виде и применим метод интервалов (см. рис.):
запишем исходное неравенство в упрощенном виде и применим метод интервалов (см. рис.):



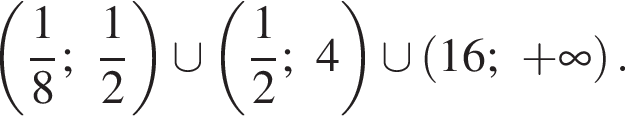
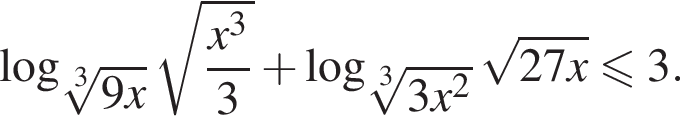



 тогда
тогда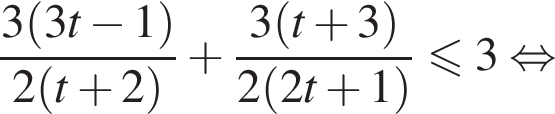






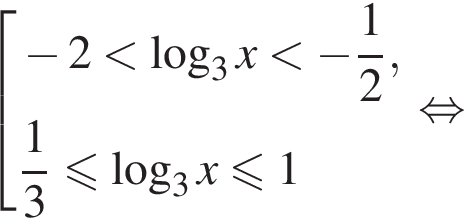
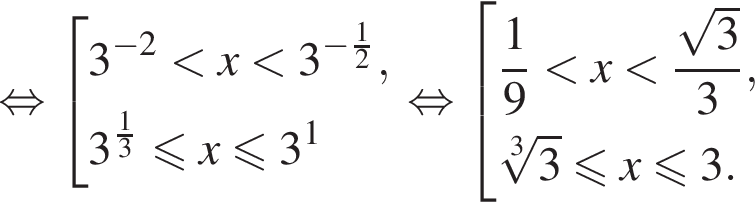








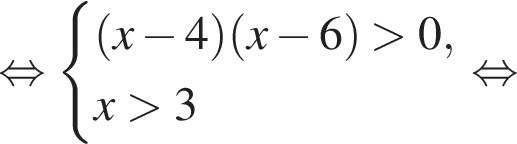












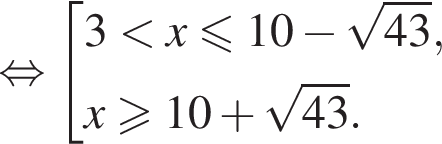


 или
или  Для положительных а такое неравенство верно, если
Для положительных а такое неравенство верно, если 







 а значит, неравенство не имеет решений. При
а значит, неравенство не имеет решений. При 


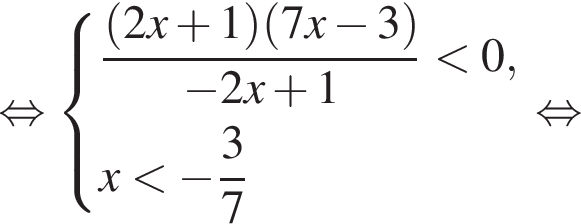










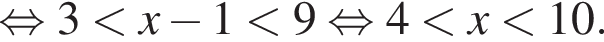

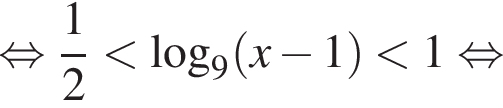









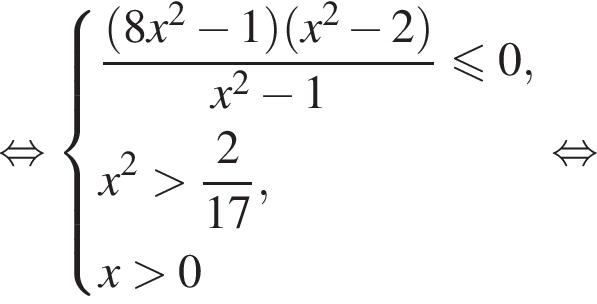







 Для таких значений x справедливо тождество:
Для таких значений x справедливо тождество: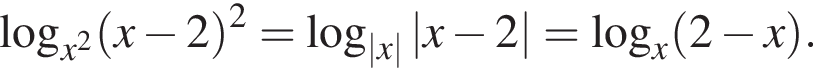



 откуда
откуда  Учитывая область определения, окончательно получаем:
Учитывая область определения, окончательно получаем: 


 получаем:
получаем:

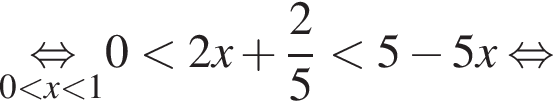


 левая часть которого отрицательна. Значит, в этом случае решений нет.
левая часть которого отрицательна. Значит, в этом случае решений нет.
 Знаменатель дроби, стоящей в левой части неравенства, положителен, поэтому на него можно умножить, не меняя знака неравенства. Таким образом,
Знаменатель дроби, стоящей в левой части неравенства, положителен, поэтому на него можно умножить, не меняя знака неравенства. Таким образом,  откуда находим, что
откуда находим, что 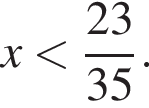 Учитывая область определения, окончательно получаем:
Учитывая область определения, окончательно получаем: 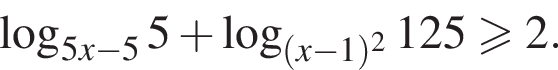



 которое определено лишь при
которое определено лишь при  При этом условии раскроем модуль в знаменателе второй дроби, получим:
При этом условии раскроем модуль в знаменателе второй дроби, получим: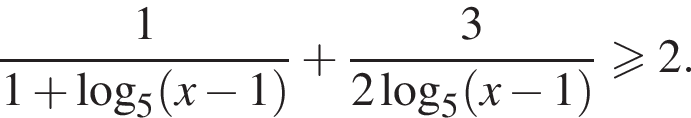
 тогда
тогда









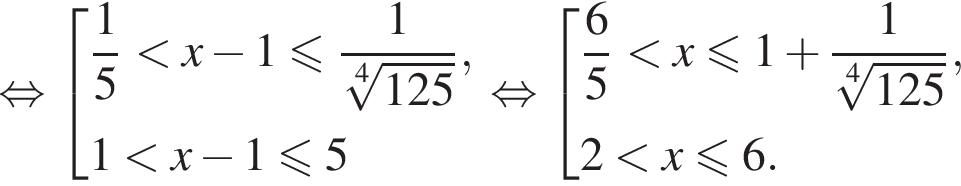


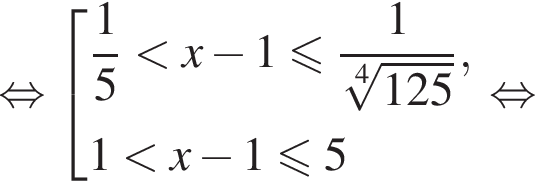


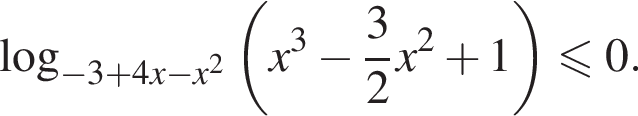

















 положительно при всех допустимых значениях x, так как неотрицательные слагаемые не равны нулю одновременно. Следовательно, обе части неравенства можно умножить на это выражение, не меняя знака неравенства. Получаем:
положительно при всех допустимых значениях x, так как неотрицательные слагаемые не равны нулю одновременно. Следовательно, обе части неравенства можно умножить на это выражение, не меняя знака неравенства. Получаем: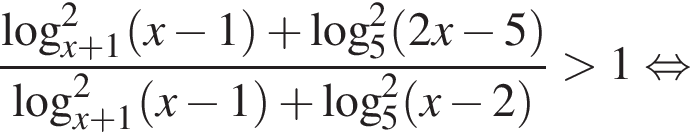



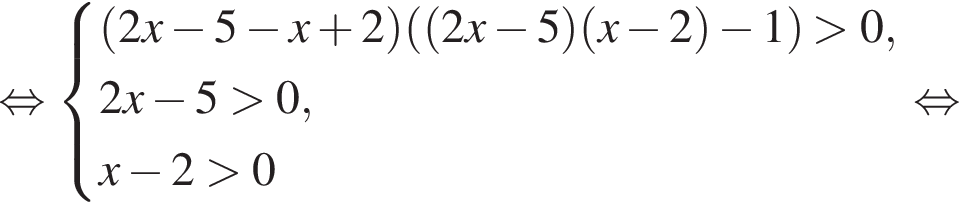







 и
и  для любых значений x, тогда
для любых значений x, тогда



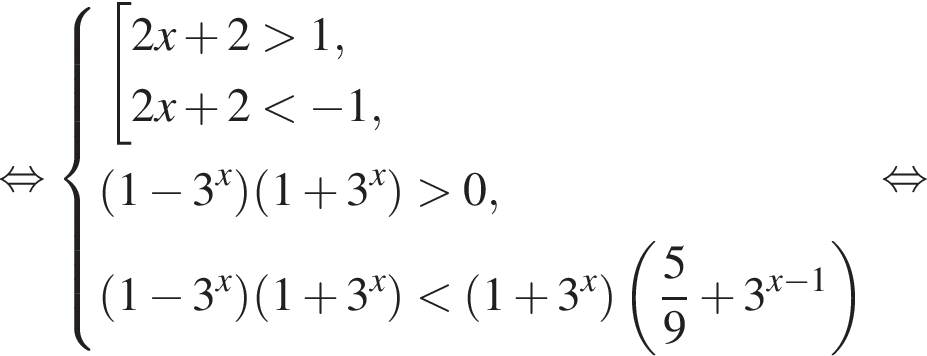











 или
или 








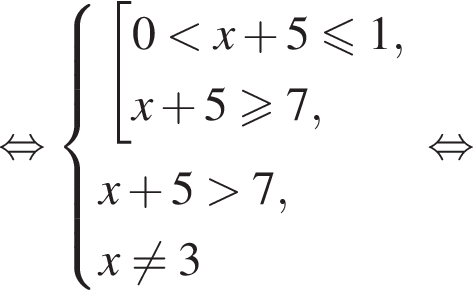









 или
или 










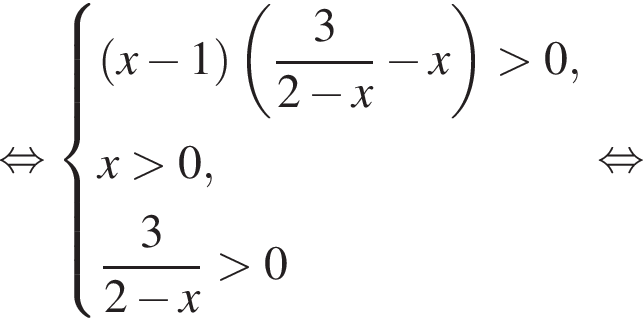




 получаем
получаем







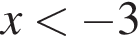 получаем
получаем





 или
или 



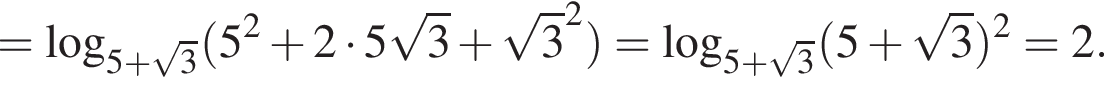













 тогда
тогда



 можно заменить на
можно заменить на  откуда находим:
откуда находим:



















 тогда
тогда






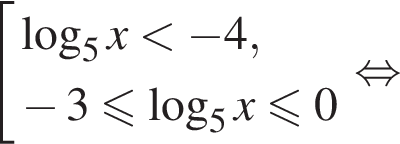



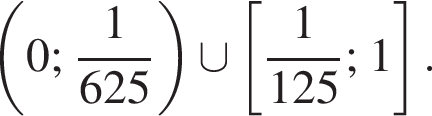






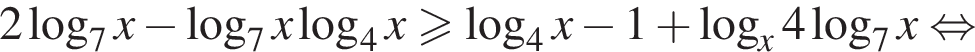





 знаменатель дроби отрицателен, а значит, знак неравенства меняется. Находим:
знаменатель дроби отрицателен, а значит, знак неравенства меняется. Находим: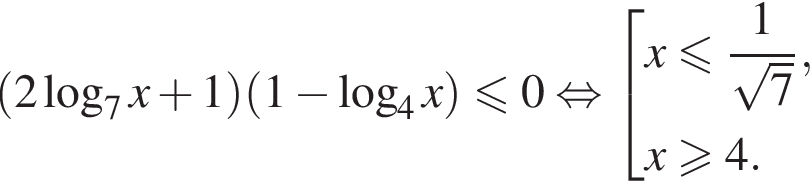



 или
или 










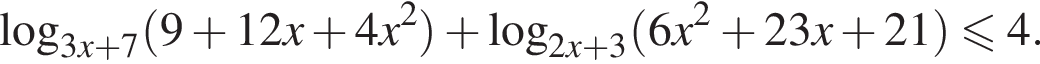




 тогда
тогда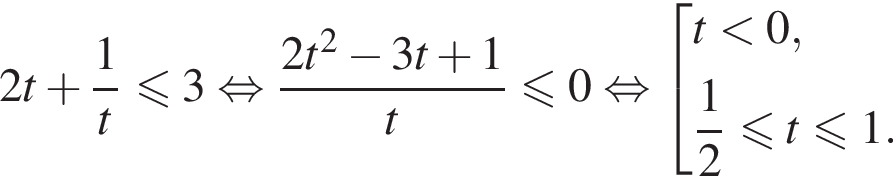







 Решая эту систему, находим область определения:
Решая эту систему, находим область определения:  На множестве X для первого неравенства, используя свойство логарифма (
На множестве X для первого неравенства, используя свойство логарифма (























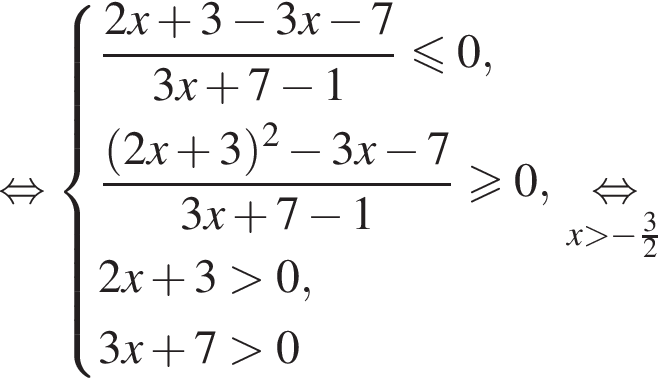














 получим:
получим:



 Пусть
Пусть  тогда
тогда





 что невозможно, или
что невозможно, или  откуда
откуда  или
или  имеем:
имеем:


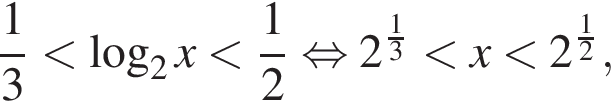

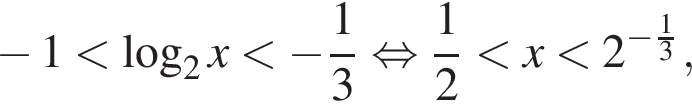

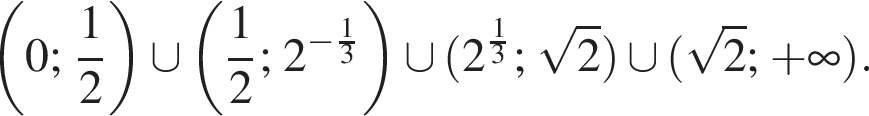

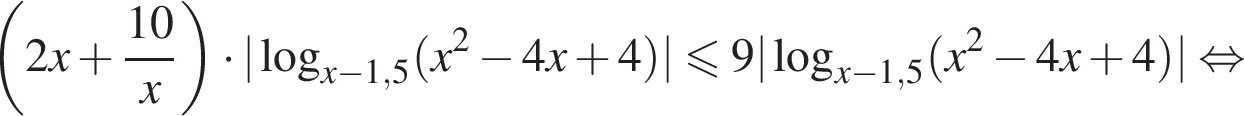

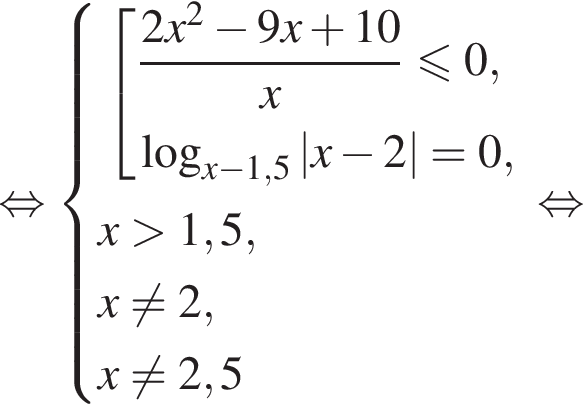








 При этих значениях x правая часть неравенства принимает значения, не превосходящие 2. Левая часть неравенства имеет вид
При этих значениях x правая часть неравенства принимает значения, не превосходящие 2. Левая часть неравенства имеет вид  где
где  Основание и аргумент логарифма, обозначенного t, больше единицы, а потому
Основание и аргумент логарифма, обозначенного t, больше единицы, а потому  исходное неравенство верно тогда и только тогда, когда обе его части равны 2. Уравнение
исходное неравенство верно тогда и только тогда, когда обе его части равны 2. Уравнение  имеет единственное решение
имеет единственное решение 

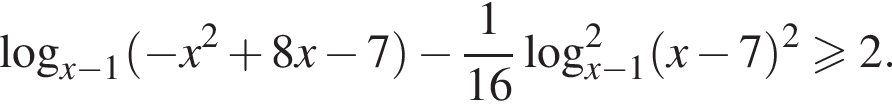
 На области определения имеем:
На области определения имеем:
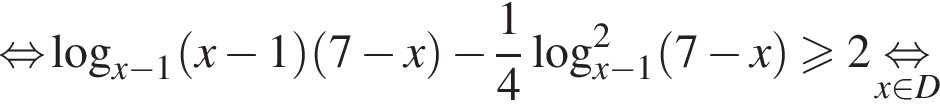
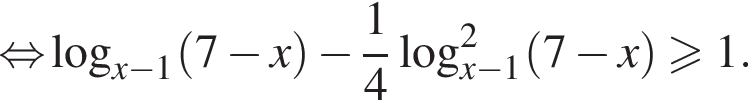
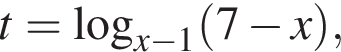 тогда
тогда








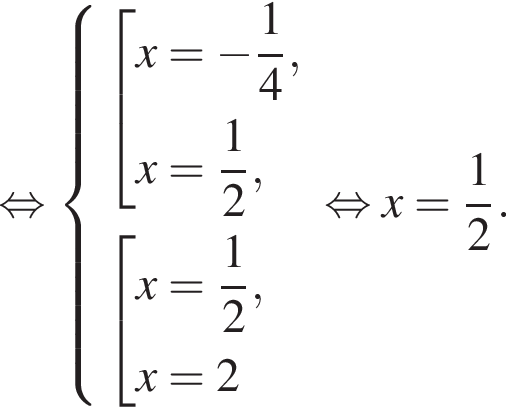

 находим:
находим:

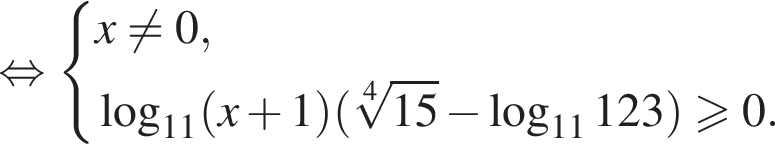

 Таким образом,
Таким образом,



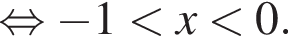



 то аргумент
то аргумент  и полученная система неравенств несовместна. Если же
и полученная система неравенств несовместна. Если же  то есть если
то есть если  находим:
находим:
