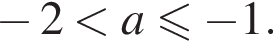Найдите все такие значения параметра a, при каждом из которых уравнение  имеет хотя бы одно решение.
имеет хотя бы одно решение.
Решение. Решение 1. Положим,  где
где  поскольку
поскольку 
Тогда исходное уравнение принимает вид  Найдем множество значений функции
Найдем множество значений функции  на отрезке [0; 2].
на отрезке [0; 2].  на промежутке [0; 2), поэтому функция убывает на отрезке [0; 2], и, следовательно, множество ее значений на отрезке [0; 2] ― отрезок
на промежутке [0; 2), поэтому функция убывает на отрезке [0; 2], и, следовательно, множество ее значений на отрезке [0; 2] ― отрезок  то есть отрезок
то есть отрезок  Таким образом, уравнение
Таким образом, уравнение  имеет решения тогда и только тогда, когда выполняются условия
имеет решения тогда и только тогда, когда выполняются условия 


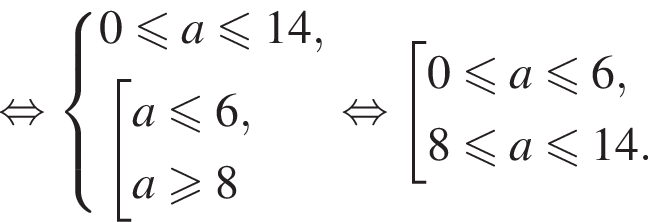



Решение 2. Положим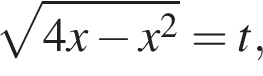 где
где  так как
так как  и рассмотрим функцию
и рассмотрим функцию  Ее производная
Ее производная  на промежутке [0; 2), поэтому функция убывает на отрезке [0; 2] и, значит, имеет на нем не более одного корня. Этот корень есть тогда и только тогда, когда одновременно выполняются два условия
на промежутке [0; 2), поэтому функция убывает на отрезке [0; 2] и, значит, имеет на нем не более одного корня. Этот корень есть тогда и только тогда, когда одновременно выполняются два условия  и
и  Таким образом, приходим к системе
Таким образом, приходим к системе




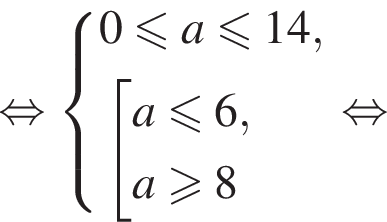
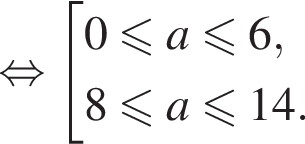
Решение 3 (Указание). Построить эскиз графика функции  на отрезке [0; 2] (см. решение 1) и исследовать взаимное расположение графика этой функции и прямой
на отрезке [0; 2] (см. решение 1) и исследовать взаимное расположение графика этой функции и прямой 
Ответ: 
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обосновано получен ответ, отличающийся от верного только исключением и/или включением граничных точек ИЛИ Ответ неверен вследствие одной вычислительной ошибки (описки), не повлиявшей на ход решения и не упростившей задачу. | 3 |
| С помощью верного рассуждения получены искомые промежутки значений | 2 |
Задача сведена к исследованию взаимного расположения графика функции  и прямой и прямой  ИЛИ (при аналитическом решении 1) найдено множество значений функции, но дальнейшие рассуждения неверны или отсутствуют ИЛИ (при аналитическом решении 2) установлена монотонность функции, но дальнейшие рассуждения неверны или отсутствуют. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |



 Рассмотрим две функции:
Рассмотрим две функции:  и
и 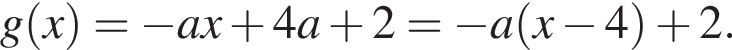 Графиком функции
Графиком функции  лежащая в верхней полуплоскости. При каждом значении a графиком функции
лежащая в верхней полуплоскости. При каждом значении a графиком функции 
 прямая не имеет общих точек с полуокружностью.
прямая не имеет общих точек с полуокружностью. проходит через точки
проходит через точки  и
и  следовательно, её угловой коэффициент
следовательно, её угловой коэффициент  При
При  прямая, заданная уравнением
прямая, заданная уравнением  имеет угловой коэффициент не больше, чем у прямой MA, и пересекает полуокружность в двух точках. При
имеет угловой коэффициент не больше, чем у прямой MA, и пересекает полуокружность в двух точках. При  прямая, заданная уравнением
прямая, заданная уравнением 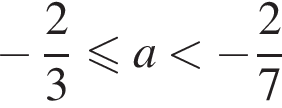 исходное уравнение имеет единственный корень. При
исходное уравнение имеет единственный корень. При  прямая не имеет общих точек с полуокружностью.
прямая не имеет общих точек с полуокружностью.
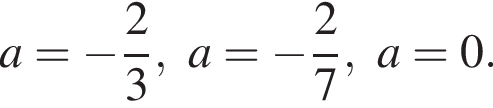 Ответ
Ответ и/или включением точки
и/или включением точки 

 или
или  имеет более двух корней.
имеет более двух корней. рассмотрим функцию
рассмотрим функцию  Раскрывая модуль, получаем:
Раскрывая модуль, получаем:
 Чтобы изучить поведение функции при положительных значениях переменной, найдем производную:
Чтобы изучить поведение функции при положительных значениях переменной, найдем производную:
 меняя знак с плюса на минус. Следовательно, эта точка является точкой максимума, причем
меняя знак с плюса на минус. Следовательно, эта точка является точкой максимума, причем  Построим эскиз графика функции (см. рис.). Из графика заключаем, что уравнение имеет три корня при
Построим эскиз графика функции (см. рис.). Из графика заключаем, что уравнение имеет три корня при 

 и
и  имеют более двух общих точек на луче
имеют более двух общих точек на луче  При a < 1 уравнение не имеет решений. При a = 1 уравнение имеет единственный корень x = 0. При
При a < 1 уравнение не имеет решений. При a = 1 уравнение имеет единственный корень x = 0. При 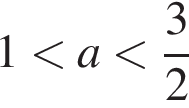 уравнение имеет два решения. Пусть m — значение a, которому соответствует точка касания графика функции
уравнение имеет два решения. Пусть m — значение a, которому соответствует точка касания графика функции  и графика функции
и графика функции  Тогда при
Тогда при  уравнение имеет три решения, при
уравнение имеет три решения, при 



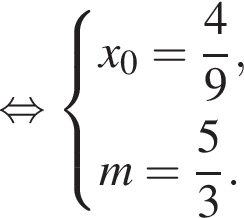


 и
и  Исследуем уравнение
Исследуем уравнение 
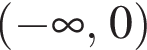 функция
функция  имеет не более одного решения на промежутке
имеет не более одного решения на промежутке  причем решение будет существовать тогда и только тогда, когда,
причем решение будет существовать тогда и только тогда, когда,  то есть при
то есть при  При
При  дискриминант которого
дискриминант которого  поэтому при
поэтому при 

 а больший корень
а больший корень  то есть при
то есть при 
 поэтому знаки корней
поэтому знаки корней  Значит, при
Значит, при  оба корня отрицательны, при
оба корня отрицательны, при  один из корней отрицательный, а другой неотрицательный, при
один из корней отрицательный, а другой неотрицательный, при  не имеет корней при
не имеет корней при  имеет один корень при
имеет один корень при  и
и  имеет два корня при
имеет два корня при 

 и
и 






 Найденные корни удовлетворяют условию (*), если
Найденные корни удовлетворяют условию (*), если a — любое число;
a — любое число;
 имеет единственный корень.
имеет единственный корень.







 то
то  Поскольку при a = 0 решением являются все положительные значения t, уравнение имеет единственное решение, если
Поскольку при a = 0 решением являются все положительные значения t, уравнение имеет единственное решение, если 



 корней нет. При
корней нет. При  имеет единственный корень
имеет единственный корень 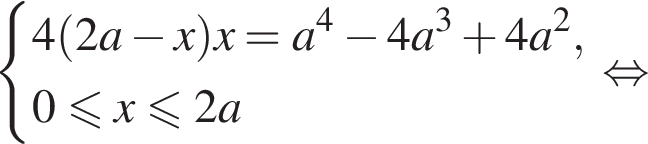

 равен
равен



 Эти корни равны
Эти корни равны и
и 
 поскольку
поскольку
 и
и 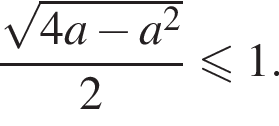

 удовлетворяют условию
удовлетворяют условию 
 имеет ровно 3 решения.
имеет ровно 3 решения.

 при любых значениях a и ещё один корень
при любых значениях a и ещё один корень 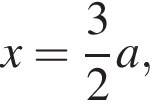 который не должен совпадать с двумя другими. Значит,
который не должен совпадать с двумя другими. Значит,  и
и 





 и рассмотрим два случая.
и рассмотрим два случая.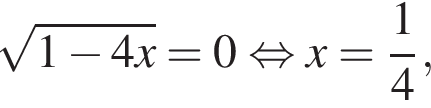 при выполнении условий
при выполнении условий 


 при условии
при условии 









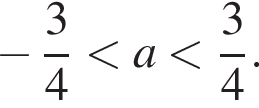

 Рассмотрим два случая.
Рассмотрим два случая. при условии
при условии  тогда
тогда 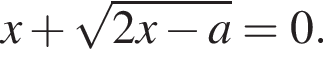 Получаем
Получаем 


 при
при 
 Рассмотрим два случая.
Рассмотрим два случая.
 при условии
при условии  Условие принимает вид
Условие принимает вид 



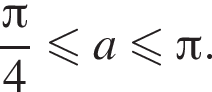
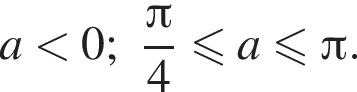



 Второй случай:
Второй случай:  из условия
из условия  Спроецируем на координатную ось xOa функции-решения
Спроецируем на координатную ось xOa функции-решения  при этом учтем
при этом учтем 
 уравнение имеет два решения, при
уравнение имеет два решения, при  — одно решение.
— одно решение. и/или
и/или  при
при  возможно, с учётом принадлежности корней указанному отрезку:
возможно, с учётом принадлежности корней указанному отрезку: 


 Получаем
Получаем  при условии
при условии 
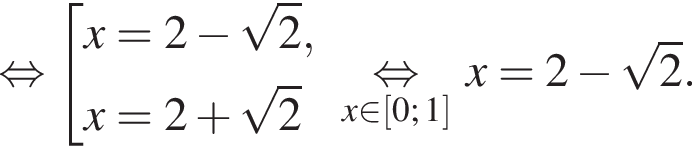




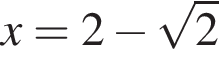 условие принимает вид
условие принимает вид  откуда
откуда  То есть в этом случае
То есть в этом случае 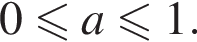

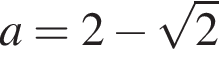 (это корень
(это корень  );
); (это корень
(это корень 
 при
при  и
и  ,
, или с учетом принадлежности корней указанному отрезку:
или с учетом принадлежности корней указанному отрезку: 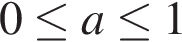 и
и 

 неограниченно возрастает на области определения. Поэтому уравнение имеет хотя бы один корень тогда и только тогда, когда наименьшее значение функции f(x) не превосходит единицы.
неограниченно возрастает на области определения. Поэтому уравнение имеет хотя бы один корень тогда и только тогда, когда наименьшее значение функции f(x) не превосходит единицы. при
при  Рассмотрим два случая:
Рассмотрим два случая:  При
При  и ее наименьшее значение равно
и ее наименьшее значение равно  Получаем неравенство
Получаем неравенство  откуда
откуда 
 и ее наименьшее значение равно
и ее наименьшее значение равно  Получаем неравенство
Получаем неравенство  откуда
откуда  Учитывая условие
Учитывая условие  получаем
получаем 


 при одном из условий
при одном из условий  , возможно, с включением граничных точек
, возможно, с включением граничных точек ;
;  ;
;  или
или  , возможно, с включение граничных точек
, возможно, с включение граничных точек

 и
и  Чтобы уравнение имело три различных корня, требуется, чтобы при
Чтобы уравнение имело три различных корня, требуется, чтобы при  выполнялось неравенство
выполнялось неравенство  а также чтобы были выполнены условия
а также чтобы были выполнены условия 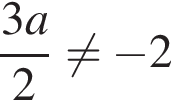 и
и 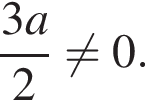 Получаем систему неравенств:
Получаем систему неравенств:






 множества значений a
множества значений a 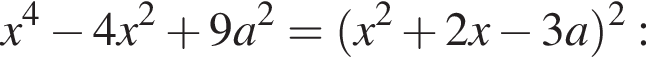
 и задача верно сведена к исследованию полученных корней при условии
и задача верно сведена к исследованию полученных корней при условии 


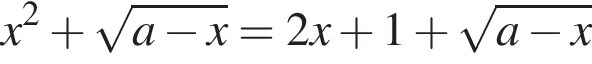 равносильно системе
равносильно системе 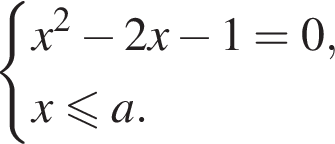 Эта система имеет единственный корень
Эта система имеет единственный корень  на отрезке [−1; 1] при
на отрезке [−1; 1] при  и не имеет корней на этом отрезке при других значениях a.
и не имеет корней на этом отрезке при других значениях a. равносильно уравнению
равносильно уравнению  Оно имеет единственный корень
Оно имеет единственный корень  на отрезке [−1; 1] при
на отрезке [−1; 1] при  и не имеет корней на этом отрезке при других значениях a.
и не имеет корней на этом отрезке при других значениях a. уравнение
уравнение  и
и 

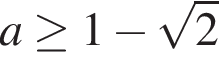







 его левая часть положительна, а правая — отрицательна.
его левая часть положительна, а правая — отрицательна.  Первый график — прямая с угловым коэффициентом 1, проходящая через начало координат. Второй график является графиком функции
Первый график — прямая с угловым коэффициентом 1, проходящая через начало координат. Второй график является графиком функции  сдвинутым вдоль оси абсцисс на a единиц. Из графика видим, что на отрезке [0; 1] уравнение имеет решение 0 при
сдвинутым вдоль оси абсцисс на a единиц. Из графика видим, что на отрезке [0; 1] уравнение имеет решение 0 при  уравнение имеет единственное решение.
уравнение имеет единственное решение.

 и рассмотрим два случая.
и рассмотрим два случая. при выполнении условий
при выполнении условий




 при условии
при условии 





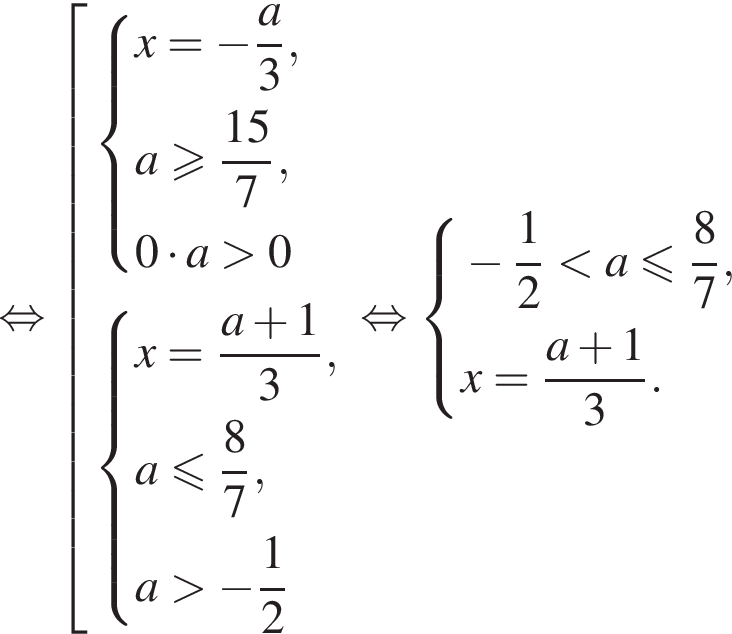


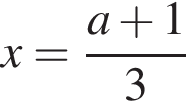 совпадают при
совпадают при 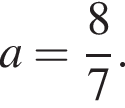
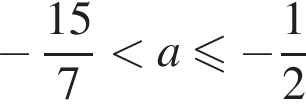 и
и 

 и / или
и / или 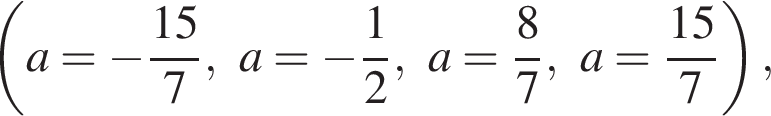 но неверно определены промежутки значений a
но неверно определены промежутки значений a  или
или  возможно, с исключением граничной точки выполнены все решения
возможно, с исключением граничной точки выполнены все решения

 и
и  Тогда уравнение примет вид
Тогда уравнение примет вид (⁎)
(⁎) 

 Таким образом, исходное уравнение имеет хотя бы одно решение при
Таким образом, исходное уравнение имеет хотя бы одно решение при 

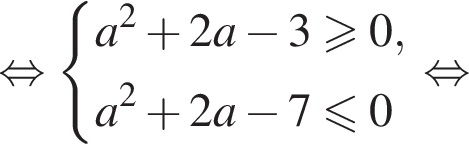


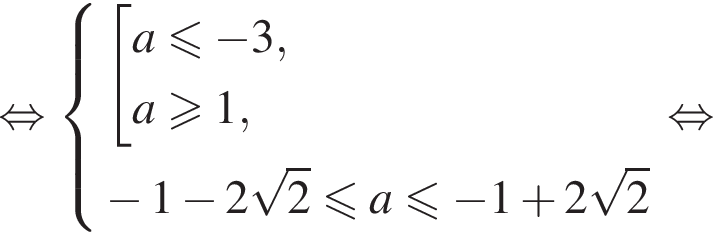
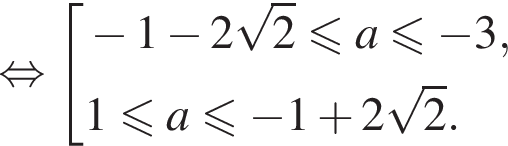
 (⁎), тогда исходное уравнение можно записать в виде
(⁎), тогда исходное уравнение можно записать в виде  или
или  (⁎⁎).
(⁎⁎).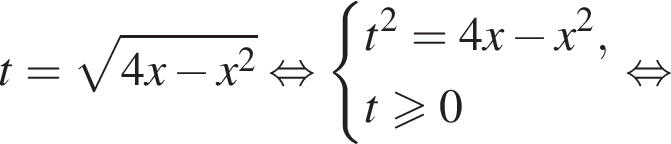





 (см. рис.).
(см. рис.). 














 :
: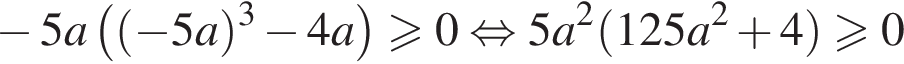




 или
или 


 и сделаем замену
и сделаем замену  где
где 
 тогда уравнение примет вид
тогда уравнение примет вид  Функция
Функция  Тем самым задача свелась к нахождению параметра a, при котором уравнение
Тем самым задача свелась к нахождению параметра a, при котором уравнение  имеет хотя бы один корень
имеет хотя бы один корень 




 Следовательно, система имеет решения при
Следовательно, система имеет решения при  то есть при
то есть при 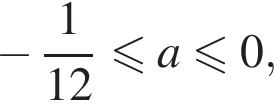


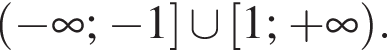 Пусть
Пусть  тогда, чтобы исходное уравнение имело два различных корня, необходимо и достаточно, чтобы уравнение
тогда, чтобы исходное уравнение имело два различных корня, необходимо и достаточно, чтобы уравнение 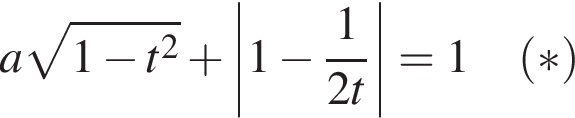
 Рассмотрим два случая раскрытия модуля.
Рассмотрим два случая раскрытия модуля. то имеем:
то имеем: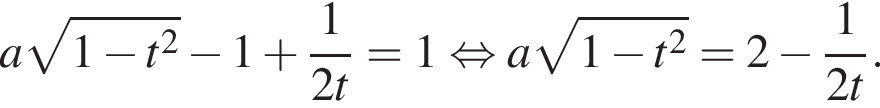


 где
где  проходит через точку
проходит через точку  Найдём значение
Найдём значение 


 то имеем:
то имеем:


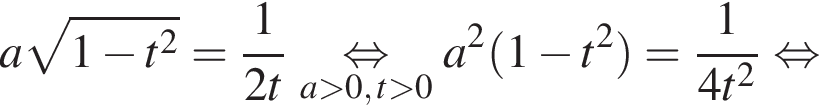



 С учётом условия
С учётом условия  Тогда уравнение не имеет решений при
Тогда уравнение не имеет решений при  имеет одно решение при
имеет одно решение при  имеет два решения при
имеет два решения при  где
где  уравнение (⁎) при
уравнение (⁎) при 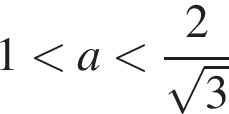 — три решения, при
— три решения, при  — два решения, при
— два решения, при  — одно решение.
— одно решение.

 и имеет бесконечно много решений.
и имеет бесконечно много решений. и
и  — имеют смысл при
— имеют смысл при  При таких значениях a и x имеем
При таких значениях a и x имеем  Значит, в этом случае уравнение
Значит, в этом случае уравнение 

 и
и 
 Тогда функция
Тогда функция  определена при
определена при  непрерывна и строго возрастает на своей области определения. Следовательно, область значений функции
непрерывна и строго возрастает на своей области определения. Следовательно, область значений функции 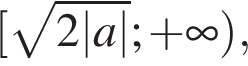 причём каждое своё значение функция
причём каждое своё значение функция 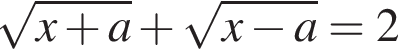 и равносильное ему исходное уравнение
и равносильное ему исходное уравнение  то есть при
то есть при  и
и 







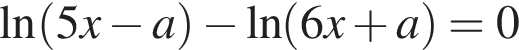 при условии
при условии  Получаем:
Получаем:




 Корни уравнения
Корни уравнения  совпадают при
совпадают при 



 и/или
и/или 



 но неверно определены промежутки значений a
но неверно определены промежутки значений a
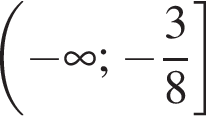 или
или  возможно, с исключением граничных точек
возможно, с исключением граничных точек
 и имеет единственное решение. При a < 0 уравнение
и имеет единственное решение. При a < 0 уравнение  и при всех таких x выполнены неравенства
и при всех таких x выполнены неравенства 
 и равносильно на этом промежутке уравнениям
и равносильно на этом промежутке уравнениям  и
и  При
При  это уравнение не имеет решений на промежутке
это уравнение не имеет решений на промежутке  так как для всех x из этого промежутка выполнены неравенства
так как для всех x из этого промежутка выполнены неравенства 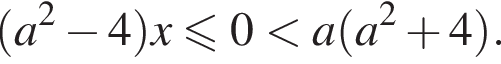 При
При  это уравнение имеет единственное решение
это уравнение имеет единственное решение  принадлежащее промежутку
принадлежащее промежутку 
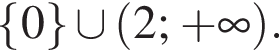





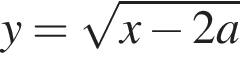 получается из графика
получается из графика  смещением на 2a вправо (при отрицательных значениях a — влево). График функции
смещением на 2a вправо (при отрицательных значениях a — влево). График функции  получается из графика
получается из графика  смещением на 2 вверх и на 2a влево (при отрицательных значениях a — вправо). Уравнение будет иметь решения тогда и только тогда, когда графики левой и правой частей имеет общие точки. Изобразим граничные случаи.
смещением на 2 вверх и на 2a влево (при отрицательных значениях a — вправо). Уравнение будет иметь решения тогда и только тогда, когда графики левой и правой частей имеет общие точки. Изобразим граничные случаи. координаты которой
координаты которой  находится не ниже графика
находится не ниже графика 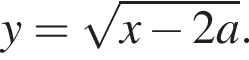 Найдём значения параметра, подставив координаты этой точки в
Найдём значения параметра, подставив координаты этой точки в  :
:




 координаты которой
координаты которой  находится не выше графика
находится не выше графика 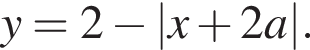 Найдём значения параметра, подставив координаты этой точки в
Найдём значения параметра, подставив координаты этой точки в  :
: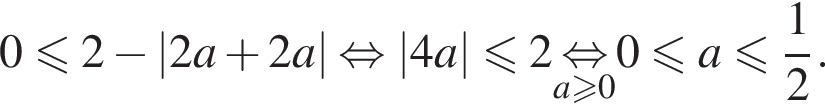
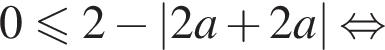

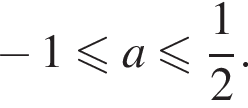
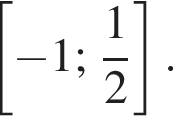

 Выделим в левой части полный квадрат:
Выделим в левой части полный квадрат:
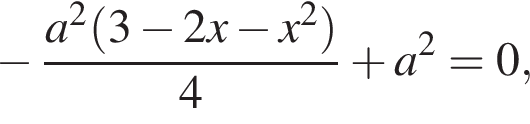



 которое имеет единственное решение a = −1. Следовательно, при a = −1 уравнение имеет решение x = −1.
которое имеет единственное решение a = −1. Следовательно, при a = −1 уравнение имеет решение x = −1. то a = 0. Получаем уравнение x2 = 0, которое имеет решение x = 0.
то a = 0. Получаем уравнение x2 = 0, которое имеет решение x = 0.


 и
и  равно
равно  Тогда величина
Тогда величина  выражает расстояние между точкой
выражает расстояние между точкой 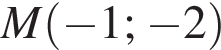 и точкой
и точкой  где
где  а
а  выражает расстояние между точкой
выражает расстояние между точкой  и точкой
и точкой  Заметим, что в силу равенства координат точка T лежит на прямой
Заметим, что в силу равенства координат точка T лежит на прямой  причём равенство достигается, только если T является точкой пересечения прямой
причём равенство достигается, только если T является точкой пересечения прямой 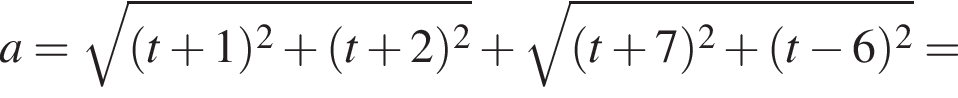













 корень
корень 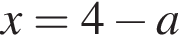 принадлежит отрезку [0; 2] при
принадлежит отрезку [0; 2] при  Корень
Корень  при
при  или
или 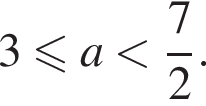


 значит, в этом случае корнями могут быть числа
значит, в этом случае корнями могут быть числа 

 при
при  значит, в этом случае корнями уравнения могут быть числа
значит, в этом случае корнями уравнения могут быть числа 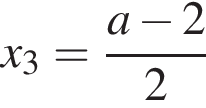 и
и 
 Отдельно отметим, когда корни совпадают:
Отдельно отметим, когда корни совпадают:  при
при  корнями исходного уравнения являются числа
корнями исходного уравнения являются числа 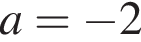 корнями исходного уравнения являются числа
корнями исходного уравнения являются числа  корнями исходного уравнения являются числа
корнями исходного уравнения являются числа  — 4 корня;
— 4 корня; и
и  — 2 корня;
— 2 корня; корнями исходного уравнения являются числа
корнями исходного уравнения являются числа  — 3 корня;
— 3 корня; a = 0, a > 2.
a = 0, a > 2. тогда получим
тогда получим
 и
и  множества значений a, возможно с включением границ
множества значений a, возможно с включением границ











 и
и  совпадают при
совпадают при  Корни
Корни 
 не имеет корней;
не имеет корней; имеет один корень
имеет один корень 
 имеет два корня
имеет два корня 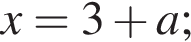
 имеет два корня
имеет два корня 
 имеет один корень
имеет один корень  не имеет корней.
не имеет корней.

 имеет корни (хотя бы один), из которых ровно один отрицательный.
имеет корни (хотя бы один), из которых ровно один отрицательный.



 является парабола с вершиной в точке
является парабола с вершиной в точке  проходящая через точки
проходящая через точки 
 и
и  Условию
Условию  удовлетворяют все точки, лежащие левее прямой
удовлетворяют все точки, лежащие левее прямой 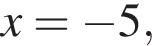 включая саму прямую, условию
включая саму прямую, условию  удовлетворяют все точки лежащие правее прямой
удовлетворяют все точки лежащие правее прямой  включая саму прямую. Таким образом, графиком системы, а значит, и графиком исходного уравнения, является парабола
включая саму прямую. Таким образом, графиком системы, а значит, и графиком исходного уравнения, является парабола  уравнение не имеет корней;
уравнение не имеет корней; уравнение имеет единственный корень
уравнение имеет единственный корень  что удовлетворяет условию задачи;
что удовлетворяет условию задачи; уравнение имеет два отрицательных корня;
уравнение имеет два отрицательных корня; уравнение имеет один отрицательный корень, что удовлетворяет условию задачи;
уравнение имеет один отрицательный корень, что удовлетворяет условию задачи;  уравнение имеет два отрицательных корня;
уравнение имеет два отрицательных корня; при
при 

 и/или
и/или  возможно, с выключением граничных точек или получен неверный ответ из-за вычислительной ошибки, но при этом верно выполнены все шаги решения
возможно, с выключением граничных точек или получен неверный ответ из-за вычислительной ошибки, но при этом верно выполнены все шаги решения относительно точек при
относительно точек при 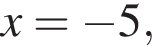
 и
и  возможно с выключением граничных точек
возможно с выключением граничных точек 
 Рассмотрим векторы
Рассмотрим векторы 






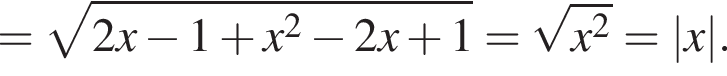






 то есть в случае, когда векторы
то есть в случае, когда векторы  Следовательно, векторы
Следовательно, векторы 

 :
:



 убеждаемся, что они являются его решениями. Таким образом, при наибольшем возможном значении параметра а исходное уравнение имеет корни
убеждаемся, что они являются его решениями. Таким образом, при наибольшем возможном значении параметра а исходное уравнение имеет корни 









 уравнение имеет единственное решение
уравнение имеет единственное решение 

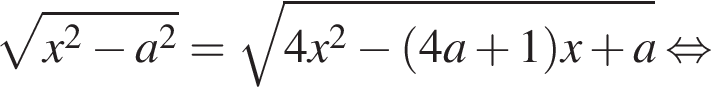



 При неотрицательных значениях x неравенству
При неотрицательных значениях x неравенству  удовлетворяют точки лежащие одновременно не ниже прямой
удовлетворяют точки лежащие одновременно не ниже прямой  и не выше прямой
и не выше прямой 




 не имеет корней;
не имеет корней; имеет один корень;
имеет один корень; имеет два корня;
имеет два корня; имеет один корень;
имеет один корень;


 при условии
при условии  Решим уравнение
Решим уравнение 
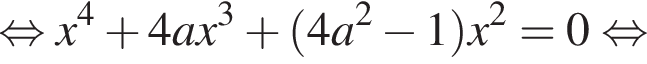

 или
или 
 При
При  имеем
имеем  При остальных значениях a числа 0,
При остальных значениях a числа 0, 
 различны.
различны.  при всех значениях a.
при всех значениях a.  получаем:
получаем: 
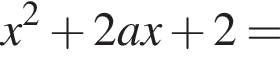



 При
При  получаем:
получаем: 

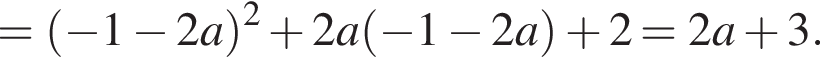


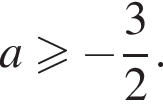 Таким образом, исходное уравнение имеет ровно три различных корня при
Таким образом, исходное уравнение имеет ровно три различных корня при 









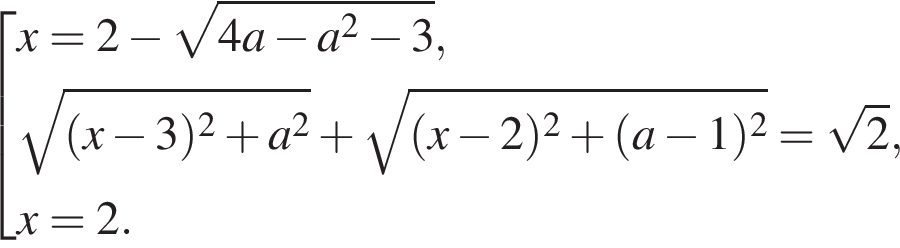
 принадлежащая также и прямой
принадлежащая также и прямой 

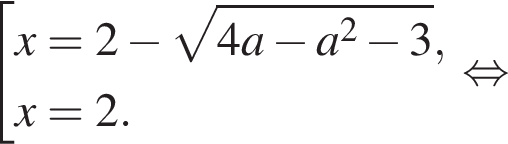

 и
и  выделена зеленым) при
выделена зеленым) при 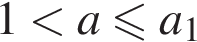 и при
и при  где a1 и a2 соответственно — ординаты точек
где a1 и a2 соответственно — ординаты точек


 и при
и при 




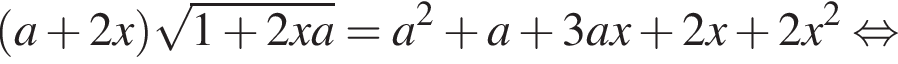








 где
где  и
и  График второй системы — лежащая не ниже прямой
График второй системы — лежащая не ниже прямой  дуга CFD окружности с центром в точке
дуга CFD окружности с центром в точке 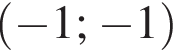 и радиусом
и радиусом 

 и
и  где
где 


 :
: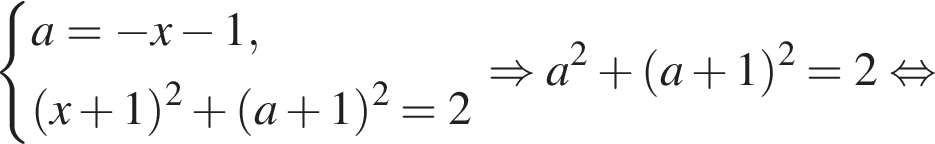





 Найдём ординату точки E — одной из точек пересечения прямой
Найдём ординату точки E — одной из точек пересечения прямой  и окружности
и окружности 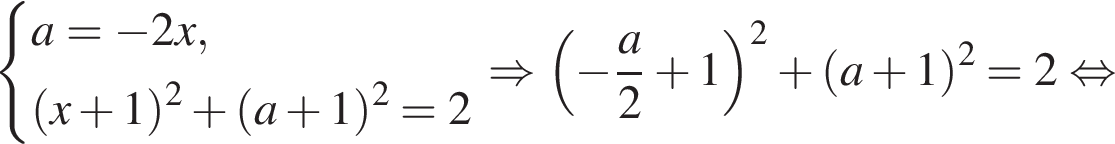






 и
и 





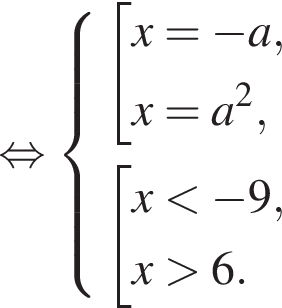
 если
если  или
или  если
если  или
или 
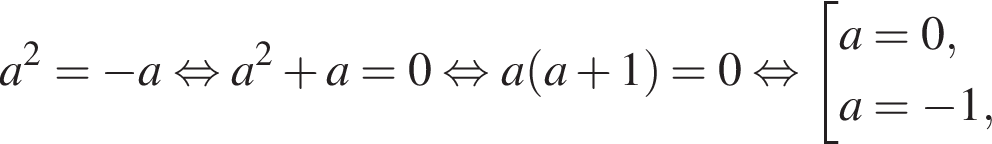



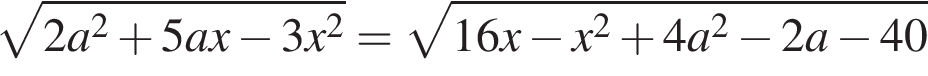

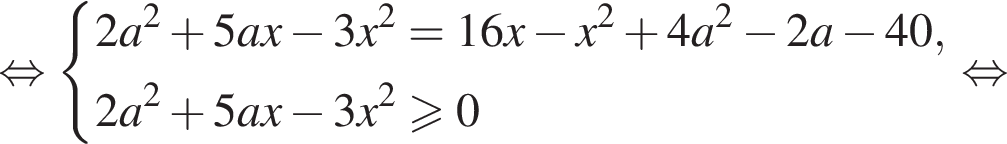





 и
и 

 и
и  :
: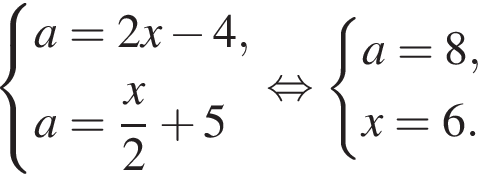
 проходит через точки
проходит через точки  и
и  а прямая
а прямая 




 уравнение равносильно следующим:
уравнение равносильно следующим: 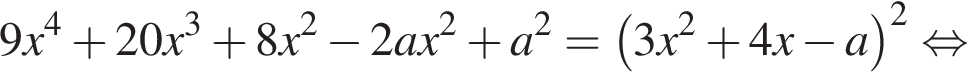




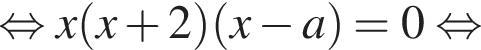
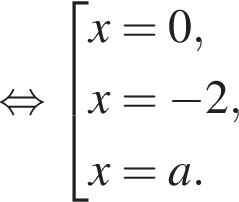
 Рассмотрим условия совпадения корней. При
Рассмотрим условия совпадения корней. При  уравнение имеет не более двух различных корней. При остальных значениях a числа 0, −2, a различны. При
уравнение имеет не более двух различных корней. При остальных значениях a числа 0, −2, a различны. При  Это выражение неотрицательно при
Это выражение неотрицательно при 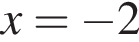 получаем
получаем  Это выражение неотрицательно при
Это выражение неотрицательно при  Это выражение неотрицательно при
Это выражение неотрицательно при  или
или  и при
и при