1. Тип Д19 C7 № 505693 

Классификатор алгебры: Последовательности и прогрессии
Сложные задания на числа и их свойства. Последовательности и прогрессии
i
a1, a2, a3, ... – возрастающая последовательность натуральных чисел. Известно, что  для любого
для любого ![]() Найти:
Найти:
а) a100;
б) a1983.
Решение. а) Сразу заметим, что последовательность ak строго возрастает. Действительно, предположение  немедленно приводит к противоречию:
немедленно приводит к противоречию:  Кроме того,
Кроме того, ![]() (в противном случае
(в противном случае  ). Отсюда следует, что
). Отсюда следует, что ![]() для всех
для всех ![]() С другой стороны,
С другой стороны,  Поэтому
Поэтому 








 А поскольку
А поскольку  то
то  для всех k от 81 до 162. В частности,
для всех k от 81 до 162. В частности, 
б) 

 Поскольку
Поскольку  то
то  для всех k от 243 до 486. В частности,
для всех k от 243 до 486. В частности,  а значит,
а значит, 


Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Верно получены все перечисленные (см. критерий на 1 балл) результаты. | 4 |
| Верно получены три из перечисленных (см. критерий на 1 балл) результатов. | 3 |
| Верно получены два из перечисленных (см. критерий на 1 балл) результатов. | 2 |
| Верно получен один из следующий результатов: — обоснованное решение в п. а; — пример в п. б; — искомая оценка в п. в; — пример в п. в, обеспечивающий точность предыдущей оценки. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 4 |
Классификатор алгебры: Последовательности и прогрессии
 при некотором натуральном
при некотором натуральном  но
но  (при этом
(при этом  из условия). Но наибольшими числами, меньшими D и делящимися на 1005 и 1006, являются числа
из условия). Но наибольшими числами, меньшими D и делящимися на 1005 и 1006, являются числа 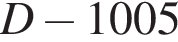 и
и 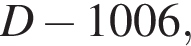 соответственно; поэтому
соответственно; поэтому 
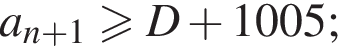 отсюда
отсюда 

 подходит, например, последовательность всех чисел, кратных 1005, но не кратных 97 (заметим, что 1005 не кратно 97).
подходит, например, последовательность всех чисел, кратных 1005, но не кратных 97 (заметим, что 1005 не кратно 97). в которой при каждом k член последовательности xk является корнем уравнения
в которой при каждом k член последовательности xk является корнем уравнения 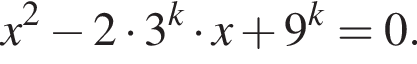
 Следовательно, формула общего члена последовательности имеет вид
Следовательно, формула общего члена последовательности имеет вид 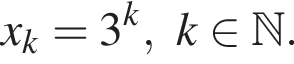
 тогда число
тогда число  содержит в десятичной записи более семи цифр. Легко убедитьcя, что условию задачи удовлетворяет число
содержит в десятичной записи более семи цифр. Легко убедитьcя, что условию задачи удовлетворяет число  то есть
то есть 
 Для того, чтобы оно было наименьшим, оно не должно иметь других делителей, то есть это число 6561.
Для того, чтобы оно было наименьшим, оно не должно иметь других делителей, то есть это число 6561.
 или
или  Отсюда получаем равенство
Отсюда получаем равенство  Последнее равенство возможно только при выполнении условий
Последнее равенство возможно только при выполнении условий  которое не является квадратом.
которое не является квадратом. Тогда
Тогда  Заметим, что
Заметим, что  Отсюда
Отсюда

 (выражения в скобках равны нулю).
(выражения в скобках равны нулю).  следовательно,
следовательно,  Поэтому единиц в последовательности бесконечное число.
Поэтому единиц в последовательности бесконечное число.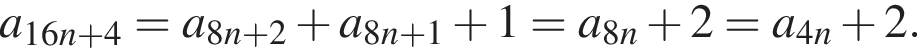
 либо не изменяется, либо уменьшается. Так как по условию исходное расположение повторяется через n минут (а значит, и через
либо не изменяется, либо уменьшается. Так как по условию исходное расположение повторяется через n минут (а значит, и через  Так как
Так как  при всех
при всех 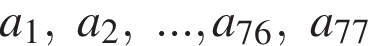 — типы деталей (A или B), которые стояли исходно на конвейере и добавлялись в последующие моменты. Мы показали, что при любом i среди
— типы деталей (A или B), которые стояли исходно на конвейере и добавлялись в последующие моменты. Мы показали, что при любом i среди  38 раз встречается A и 37 раз встречается B и тогда
38 раз встречается A и 37 раз встречается B и тогда  либо все наоборот. В любом случае при каждом i среди
либо все наоборот. В любом случае при каждом i среди  A и B встречаются по 38 раз.
A и B встречаются по 38 раз. A и B встречаются по 38 раз и среди
A и B встречаются по 38 раз и среди  (при каждом i ). Таким образом, 76 – период последовательности
(при каждом i ). Таким образом, 76 – период последовательности 
 Обратно, если q — период этой последовательности, то через q минут ситуация на конвейере повторяется. Следовательно, n — минимальный период последовательности
Обратно, если q — период этой последовательности, то через q минут ситуация на конвейере повторяется. Следовательно, n — минимальный период последовательности 

 и 76 делится на
и 76 делится на  могут реализоваться.
могут реализоваться. 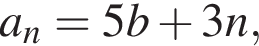 где
где 
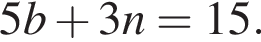 Ясно, что
Ясно, что  Проверяя
Проверяя 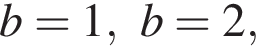 получаем, что натуральных
получаем, что натуральных  не существует.
не существует. Значит, an – арифметическая прогрессия с разностью 3.
Значит, an – арифметическая прогрессия с разностью 3. то есть
то есть  Раскроем скобки:
Раскроем скобки:  Ясно, что это равенство невозможно. Противоречие.
Ясно, что это равенство невозможно. Противоречие.
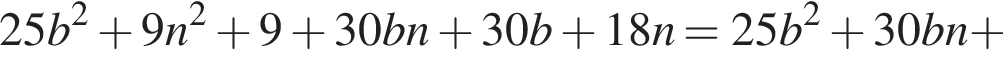








 или
или  Последнее уравнение решений в натуральных числах не имеет.
Последнее уравнение решений в натуральных числах не имеет.  По теореме Пифагора
По теореме Пифагора  Сократив на
Сократив на  получаем уравнение
получаем уравнение 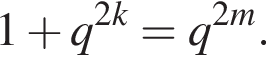 Число q — рациональное, положим
Число q — рациональное, положим  — несократимая дробь, числа p и r натуральные. Следовательно,
— несократимая дробь, числа p и r натуральные. Следовательно,  откуда
откуда  или
или 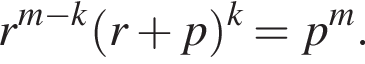 Но тогда r = 1, поскольку p и q взаимно просты, а m > k. Итак, имеем:
Но тогда r = 1, поскольку p и q взаимно просты, а m > k. Итак, имеем:  Полученное уравнение не имеет решений ни для каких натуральных р, поскольку простые делители правой части не являются делителями девой части. Противоречие.
Полученное уравнение не имеет решений ни для каких натуральных р, поскольку простые делители правой части не являются делителями девой части. Противоречие. на
на  Числа
Числа  образуют арифметическую прогрессию с разностью n и являются длинами сторон прямоугольного треугольника. Требуемое доказано.
образуют арифметическую прогрессию с разностью n и являются длинами сторон прямоугольного треугольника. Требуемое доказано. и
и  Вычитая из первого второе получим, что
Вычитая из первого второе получим, что  Тогда
Тогда  Возможны такие варианты:
Возможны такие варианты:  и
и 
 и
и  Вычитая из первого второе, получаем равенство:
Вычитая из первого второе, получаем равенство:  Если
Если  то прогрессия состоит из двух членов: 44, 33, если
то прогрессия состоит из двух членов: 44, 33, если  то
то 
 но тогда не все члены прогрессии натуральные (прогрессия получается такая: 14, 13, 12,..., −6, −7).
но тогда не все члены прогрессии натуральные (прогрессия получается такая: 14, 13, 12,..., −6, −7).
 После преобразований получается равенство:
После преобразований получается равенство:  что тоже невозможно.
что тоже невозможно.
 где
где  – натуральные. Разложим
– натуральные. Разложим  где s и t не делятся на
где s и t не делятся на  где q — некоторое натуральное число, а m — бо́льшее из чисел n и
где q — некоторое натуральное число, а m — бо́льшее из чисел n и 

 не могут быть членами одной прогрессии, так как первое меньше второго, а второе равно третьему.
не могут быть членами одной прогрессии, так как первое меньше второго, а второе равно третьему.

 что верно при
что верно при 
 поэтому n — делитель
поэтому n — делитель  то есть это делитель, меньший парного к нему (в произведении с которым он дает 246). Значит,
то есть это делитель, меньший парного к нему (в произведении с которым он дает 246). Значит, 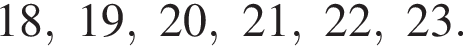
 б) 41; в) 6.
б) 41; в) 6.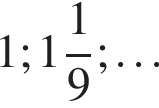
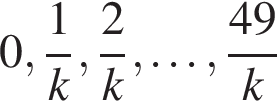 содержит ровно
содержит ровно 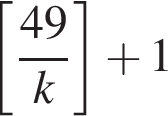 целых чисел. Это позволяет сразу привести примеры:
целых чисел. Это позволяет сразу привести примеры:

 для всех чисел до 10.
для всех чисел до 10.
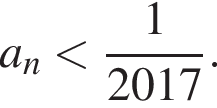
 — возрастающая функция при натуральных n и
— возрастающая функция при натуральных n и  имеем
имеем  Ответ
Ответ 
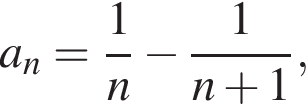 то
то 
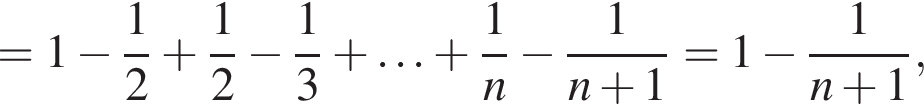
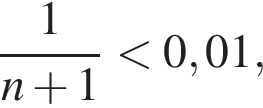 откуда
откуда  Ответ
Ответ 
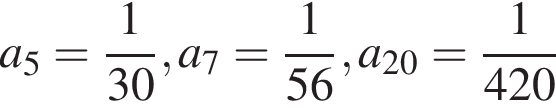 образуют арифметическую прогрессию.
образуют арифметическую прогрессию.

 то
то  откуда
откуда  или
или  но
но 
 причем
причем 
 то есть
то есть 


 поэтому d четно, но тогда
поэтому d четно, но тогда 
 Нет; в)
Нет; в) 
 Только
Только 
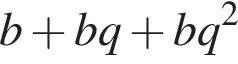 кратны. Тогда
кратны. Тогда 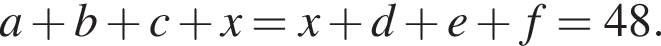
 то
то  и это вполне возможно, например, для набора 20, 10, 6, 12, 30, 2, 4. Другой вариант: 10, 11, 15, 12, 9, 13, 14.
и это вполне возможно, например, для набора 20, 10, 6, 12, 30, 2, 4. Другой вариант: 10, 11, 15, 12, 9, 13, 14.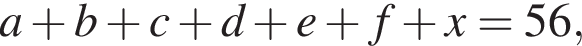 то
то  и
и  что невозможно — получить сумму без использования единицы невозможно. Значит, среди чисел есть минимум две единицы.
что невозможно — получить сумму без использования единицы невозможно. Значит, среди чисел есть минимум две единицы. То есть осталось найти наибольшее и наименьшее значение
То есть осталось найти наибольшее и наименьшее значение 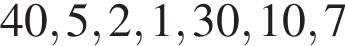 и
и  поскольку иначе
поскольку иначе 




 и
и  не являются целыми.
не являются целыми. Все ее члены не могут быть целыми.
Все ее члены не могут быть целыми. Все ее члены не могут быть целыми.
Все ее члены не могут быть целыми. то есть
то есть  Дискриминант этого уравнения равен
Дискриминант этого уравнения равен 

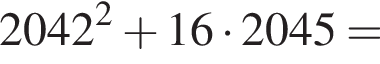




 его дискриминант равен
его дискриминант равен 
 то их произведение было бы
то их произведение было бы  что невозможно, поскольку это одно из чисел набора.
что невозможно, поскольку это одно из чисел набора.
 откуда
откуда  делится на
делится на 
 состоит из
состоит из  выполнено равенство
выполнено равенство 










 каждый следующий член равен произведению суммы цифр предыдущего члена и
каждый следующий член равен произведению суммы цифр предыдущего члена и 




 состоит из различных натуральных чисел.
состоит из различных натуральных чисел.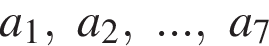 ровно три числа делятся на 24?
ровно три числа делятся на 24? ровно 9 чисел делятся на 24?
ровно 9 чисел делятся на 24? больше кратных 24, чем среди чисел
больше кратных 24, чем среди чисел 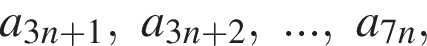 если известно, что разность прогрессии равна 1?
если известно, что разность прогрессии равна 1? и
и  ) и отсчитав
) и отсчитав 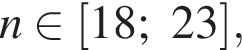 то среди
то среди  ), а среди
), а среди  из которых есть три кратных 24.
из которых есть три кратных 24. и
и  то среди первых 51 члена будут 24, 48, 72, а среди следующих 68 — только 96 и 120.
то среди первых 51 члена будут 24, 48, 72, а среди следующих 68 — только 96 и 120. при всех натуральных
при всех натуральных 




 удовлетворяет условию.
удовлетворяет условию.




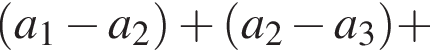



 больше
больше  минимум на 5. Аналогично с остальными разностями, поэтому минимальное значение не меньше 20. Значение 20 возможно, например, для последовательности 45, 36, 28, 21, 15, 10, 6, 3, 1, 0.
минимум на 5. Аналогично с остальными разностями, поэтому минимальное значение не меньше 20. Значение 20 возможно, например, для последовательности 45, 36, 28, 21, 15, 10, 6, 3, 1, 0. то есть
то есть 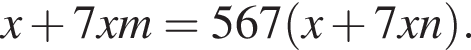 Сокращая на
Сокращая на 


 то есть
то есть  Сокращая на
Сокращая на 




 дающий остаток 1 при делении на 7, откуда, перебирая делители этого числа, получим
дающий остаток 1 при делении на 7, откуда, перебирая делители этого числа, получим  или
или  В первом случае
В первом случае  и
и  Во втором
Во втором 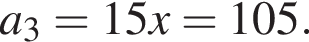

 при всех натуральных
при всех натуральных 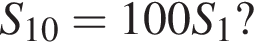
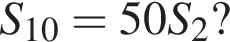


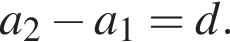




 тогда
тогда 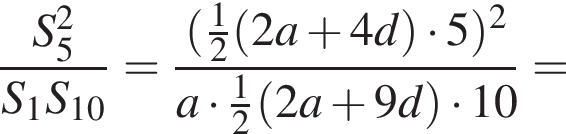


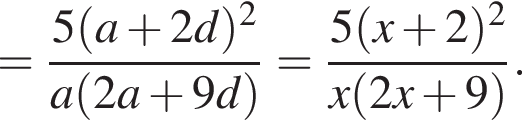



 и положительна при
и положительна при  Значит, функция убывает на
Значит, функция убывает на  и возрастает на
и возрастает на  поэтому наименьшее значение будет при
поэтому наименьшее значение будет при  и оно равно
и оно равно 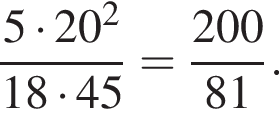 Его можно получить, например, при
Его можно получить, например, при  и
и  поэтому разность прогрессии не может быть больше
поэтому разность прогрессии не может быть больше  Значит, максимальная разность равна 44. Это значение достигается для прогрессии 11, 55, 99.
Значит, максимальная разность равна 44. Это значение достигается для прогрессии 11, 55, 99.



 или
или 

 откуда
откуда  Следовательно, последние цифры чисел образуют арифметическую прогрессию. Из второго условия тогда получаем, что и
Следовательно, последние цифры чисел образуют арифметическую прогрессию. Из второго условия тогда получаем, что и  то есть первые цифры чисел образуют арифметическую прогрессию. Ясно, что условий
то есть первые цифры чисел образуют арифметическую прогрессию. Ясно, что условий  и
и 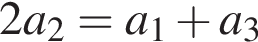 будет и достаточно для выполнения условий
будет и достаточно для выполнения условий 

 Всего есть 5 нечетных цифр и 4 четных. Выбрать две нечетных можно
Всего есть 5 нечетных цифр и 4 четных. Выбрать две нечетных можно  способами, а две четных
способами, а две четных  способами
способами способ
способ вариант.
вариант.