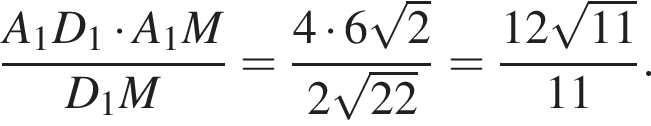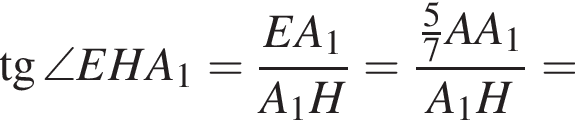В кубе ABCDA1B1C1D1 все рёбра равны 4. На его ребре BB1 отмечена точка K так, что KB = 3. Через точки K и C1 построена плоскость α, параллельная прямой BD1.
а) Докажите, что A1P : PB1 = 2 : 1, где P — точка пересечения плоскости α с ребром A1B1.
б) Найдите угол наклона плоскости α к плоскости грани BB1C1C.
Решение. а) В плоскости  через точку К проведем прямую параллельно
через точку К проведем прямую параллельно ![]() Пусть эта прямая пересекает диагональ
Пусть эта прямая пересекает диагональ ![]() в точке L. В плоскости основания
в точке L. В плоскости основания  проведем прямую
проведем прямую ![]() пусть она пересекает сторону
пусть она пересекает сторону ![]() в точке P. Треугольник KPC1 — сечение, проходящее через точки К и С1 параллельно прямой BD1. Действительно, прямая BD1 параллельна плоскости сечения, так как параллельна лежащей в нем прямой KL.
в точке P. Треугольник KPC1 — сечение, проходящее через точки К и С1 параллельно прямой BD1. Действительно, прямая BD1 параллельна плоскости сечения, так как параллельна лежащей в нем прямой KL.
В плоскости основания  через точку A1 проведем прямую параллельно C1P. Пусть она пересекает D1В1 в точке М. По теореме Фалеса имеем:
через точку A1 проведем прямую параллельно C1P. Пусть она пересекает D1В1 в точке М. По теореме Фалеса имеем:  и
и  поэтому
поэтому  Тогда
Тогда  Что и требовалось доказать.
Что и требовалось доказать.
б) Пусть теперь точка N — основание высоты ![]() прямоугольного треугольника
прямоугольного треугольника  — является проекцией наклонной PN на плоскость
— является проекцией наклонной PN на плоскость  Тогда угол PNB1 — линейный угол искомого двугранного угла. Имеем:
Тогда угол PNB1 — линейный угол искомого двугранного угла. Имеем:


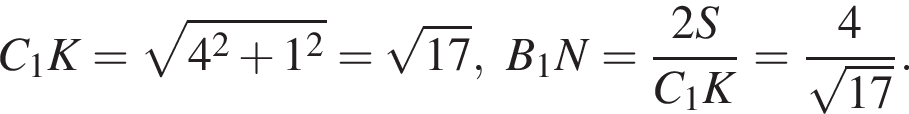



Тем самым, 
Ответ: б) 
Приведём другое решение.
б) Уравнение плоскости — ax + by + cz + d = 0.
Приведём координаты точек C1(0; 4; 4), K(4; 4; 3), 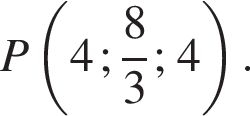
Подставив координаты указанных точек в уравнение, получим систему трёх уравнений

Вычтем из первого уравнения второе, из первого третье, из второго третье, получим следующую эквивалентную систему уравнений:

Таким образом, вектор нормали плоскости имеет вид  Откуда имеем: a = 1, b = 3, c = 4. Получаем уравнение плоскости: x + 3y + 4z + d = 0. Определим теперь коэффициент d, для этого подставим в это уравнение координаты точки C1:
Откуда имеем: a = 1, b = 3, c = 4. Получаем уравнение плоскости: x + 3y + 4z + d = 0. Определим теперь коэффициент d, для этого подставим в это уравнение координаты точки C1:

Имеем: x + 3y + 4z – 28 = 0 — уравнение плоскости PKC1. Координаты вектора нормали к плоскости 
 Координаты вектора нормали к плоскости
Координаты вектора нормали к плоскости 
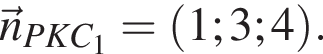 Обозначим угол между плоскостями
Обозначим угол между плоскостями ![]() и
и ![]() как
как ![]() Найдём косинус угла между плоскостями
Найдём косинус угла между плоскостями ![]() и
и 

Откуда  Может также быть получен ответ и через арктангенс:
Может также быть получен ответ и через арктангенс: 
Приведём идею решения Евгения Матвеева.
Введём систему координат с центром в точке  Уравнение плоскости сечения C1PK в отрезках
Уравнение плоскости сечения C1PK в отрезках  Нормальный вектор к этой плоскости:
Нормальный вектор к этой плоскости:  нормальный вектор к плоскости BB1C1C:
нормальный вектор к плоскости BB1C1C:  Тогда
Тогда

| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) ИЛИ имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) ИЛИ при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | 1 |
| Решение не соответствует ни одному из критериев, приведённых выше | 0 |
| Максимальный балл | 3 |






 Поэтому
Поэтому 


 — искомое сечение.
— искомое сечение. а
а  Поэтому
Поэтому  Из подобия треугольников D1C1E и BME находим, что
Из подобия треугольников D1C1E и BME находим, что 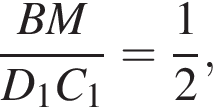 откуда BM = MA = 1. Аналогично, BN=1, треугольник BMN — равнобедренный. Опустим перпендикуляр AH на прямую
откуда BM = MA = 1. Аналогично, BN=1, треугольник BMN — равнобедренный. Опустим перпендикуляр AH на прямую  и, значит,
и, значит,  — искомый угол.
— искомый угол. Тогда
Тогда 

 Из подобия этих треугольников находим
Из подобия этих треугольников находим 
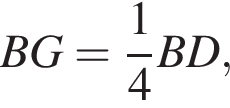 отрезок MN — средняя линия треугольника ABC. Поэтому BM = BN = 1. Таким образом, построено искомое сечение — трапеция A1C1NM.
отрезок MN — средняя линия треугольника ABC. Поэтому BM = BN = 1. Таким образом, построено искомое сечение — трапеция A1C1NM. Вычислим тангенс искомого угла:
Вычислим тангенс искомого угла: 

 Тогда, по теореме косинусов,
Тогда, по теореме косинусов,  Отсюда
Отсюда  Получается, что основание равнобедренного треугольника BMC меньше его боковой стороны, значит, угол при вершине острый. Угол же при основании равнобедренного треугольника всегда острый. Отсюда получаем требуемое.
Получается, что основание равнобедренного треугольника BMC меньше его боковой стороны, значит, угол при вершине острый. Угол же при основании равнобедренного треугольника всегда острый. Отсюда получаем требуемое.



 имеем:
имеем: 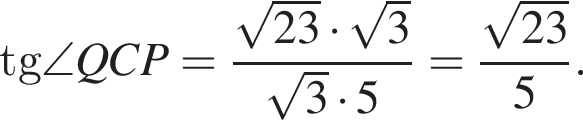


 от центра окружности основания, а хорда длиной 16, аналогично, — на расстоянии 6. Поэтому расстояние между их проекциями на плоскость, параллельную основаниям цилиндров, составляет либо 8 + 6 = 14, либо 8 − 6 = 2. Тогда расстояние между хордами составляет либо
от центра окружности основания, а хорда длиной 16, аналогично, — на расстоянии 6. Поэтому расстояние между их проекциями на плоскость, параллельную основаниям цилиндров, составляет либо 8 + 6 = 14, либо 8 − 6 = 2. Тогда расстояние между хордами составляет либо  либо
либо  По условию реализовался второй случай, в нем проекции хорд лежат по одну сторону от оси цилиндра. Значит, ось не пересекает данную плоскость в пределах цилиндра, то есть основания лежат по одну сторону от нее.
По условию реализовался второй случай, в нем проекции хорд лежат по одну сторону от оси цилиндра. Значит, ось не пересекает данную плоскость в пределах цилиндра, то есть основания лежат по одну сторону от нее.
 и, значит, AB и AH перпендикулярны хорде, то есть прямой пересечения основания с данной плоскостью.
и, значит, AB и AH перпендикулярны хорде, то есть прямой пересечения основания с данной плоскостью.

 как средняя линия треугольника ASC. Проекция прямой SB на плоскость ABC это прямая OB, где O - основание высоты пирамиды.
как средняя линия треугольника ASC. Проекция прямой SB на плоскость ABC это прямая OB, где O - основание высоты пирамиды.  так как диагонали квадрата перпендикулярны. Тогда, по теореме о трех перпендикулярах,
так как диагонали квадрата перпендикулярны. Тогда, по теореме о трех перпендикулярах,  а значит и
а значит и 





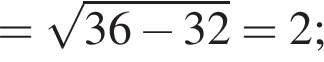



 и
и  то
то 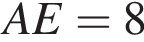 и
и  Плоскость сечения пересекает параллельные плоскости
Плоскость сечения пересекает параллельные плоскости  и
и  то и
то и  Значит,
Значит,  и
и 
 опустим перпендикуляр
опустим перпендикуляр  будет искомым. Найдём
будет искомым. Найдём  высоту
высоту  (очевидно, L — середина
(очевидно, L — середина  найдём
найдём  то есть
то есть  Тогда
Тогда 







 Кроме того, прямая
Кроме того, прямая 
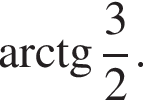
 и прямая FL пересекает прямую BD в точке K а прямая KE пересекает прямую BB1 в точке P. Тогда точка пересечения прямых B1D и KE есть точка пересечения плоскости
и прямая FL пересекает прямую BD в точке K а прямая KE пересекает прямую BB1 в точке P. Тогда точка пересечения прямых B1D и KE есть точка пересечения плоскости 
 тогда
тогда 
 Таким образом,
Таким образом, 

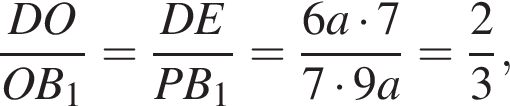 что и требовалось доказать.
что и требовалось доказать. и
и  получаем, что
получаем, что  Значит, согласно теореме о трех перпендикулярах,
Значит, согласно теореме о трех перпендикулярах,  Таким образом, угол PKB ― линейный угол искомого двугранного угла.
Таким образом, угол PKB ― линейный угол искомого двугранного угла. и
и  из треугольника PBK находим:
из треугольника PBK находим:  откуда
откуда 

 Его катеты равны
Его катеты равны  Значит,
Значит, 
 и
и  По теореме о трёх перпендикулярах, из перпендикулярности наклонной D1B и прямой AC следует перпендикулярность прямой AC проекции наклонной — прямой DB. Этим показано, что диагонали лежащего в основании прямоугольника взаимно перпендикулярны. Следовательно, этот прямоугольник является квадратом, что и требовалось доказать.
По теореме о трёх перпендикулярах, из перпендикулярности наклонной D1B и прямой AC следует перпендикулярность прямой AC проекции наклонной — прямой DB. Этим показано, что диагонали лежащего в основании прямоугольника взаимно перпендикулярны. Следовательно, этот прямоугольник является квадратом, что и требовалось доказать.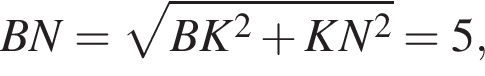


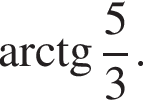
 равны по гипотенузе и катету:
равны по гипотенузе и катету: 
 Значит,
Значит,  а ABCD является квадратом.
а ABCD является квадратом. Проекцией ромба сечения на боковую грань ВСС1В1 является параллелограмм ВKС1N, площадь которого равна половине площади прямоугольника ВСС1В1 то есть 12. Поскольку
Проекцией ромба сечения на боковую грань ВСС1В1 является параллелограмм ВKС1N, площадь которого равна половине площади прямоугольника ВСС1В1 то есть 12. Поскольку  для искомого угла между плоскостями получаем:
для искомого угла между плоскостями получаем:
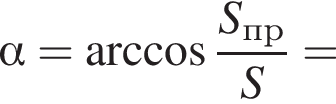


 искомый. Найдём стороны треугольника
искомый. Найдём стороны треугольника 












 и
и 




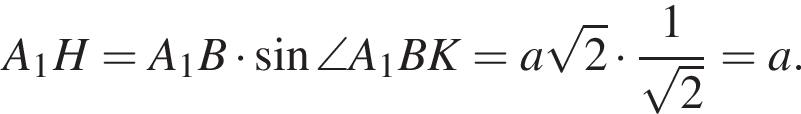
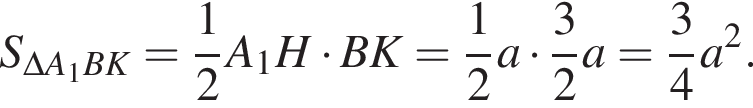
 Отношение площадей треугольников BB1C1 и A1BK. является косинусом угла
Отношение площадей треугольников BB1C1 и A1BK. является косинусом угла 


 равны по гипотенузе (AO = C1O) и острому углу, значит,
равны по гипотенузе (AO = C1O) и острому углу, значит,  Что и требовалось доказать.
Что и требовалось доказать. получаем:
получаем:




 откуда высота
откуда высота

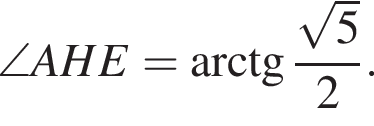
 Ответ может быть дан в другой форме:
Ответ может быть дан в другой форме:  или
или 
 вдвое больше объема пирамиды
вдвое больше объема пирамиды 
 равен
равен  Что и требовалось доказать.
Что и требовалось доказать. В треугольнике AHB найдем высоту
В треугольнике AHB найдем высоту 
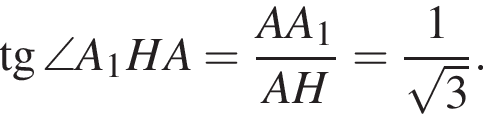

 Отсюда, по обратной теореме Пифагора, угол BSD прямой. Что и требовалось доказать.
Отсюда, по обратной теореме Пифагора, угол BSD прямой. Что и требовалось доказать. и
и  то плоскость SAC перпендикулярна прямой BD. Это значит, что плоскость SAC и есть плоскость, проходящая через точку A перпендикулярно BD.
то плоскость SAC перпендикулярна прямой BD. Это значит, что плоскость SAC и есть плоскость, проходящая через точку A перпендикулярно BD. Так как треугольник ASO — равнобедренный,
Так как треугольник ASO — равнобедренный,  Следовательно, искомый угол равен углу OMD. Найдем стороны треугольника OMD:
Следовательно, искомый угол равен углу OMD. Найдем стороны треугольника OMD:





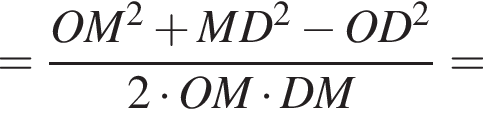


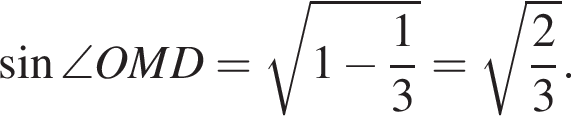



 и
и 

 Пусть R — радиус основания цилиндра. Тогда, по теореме синусов
Пусть R — радиус основания цилиндра. Тогда, по теореме синусов 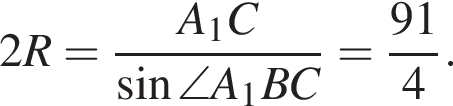
 Что и требовалось доказать.
Что и требовалось доказать.
 Следовательно, так же относятся и объемы пирамид AKCM и BKCM.
Следовательно, так же относятся и объемы пирамид AKCM и BKCM.


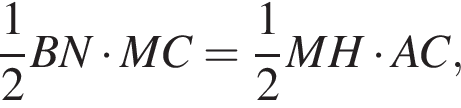 откуда
откуда





 Плоскость NMP параллельна BC и содержит NK, таким образом NMP искомая плоскость α. По теореме о пропорциональных отрезках имеем:
Плоскость NMP параллельна BC и содержит NK, таким образом NMP искомая плоскость α. По теореме о пропорциональных отрезках имеем:  Таким образом, PM параллельна SA, значит, SA параллельна α.
Таким образом, PM параллельна SA, значит, SA параллельна α.  Таким образом, угол между плоскостью
Таким образом, угол между плоскостью  где F — середина BC, а O — центр основания пирамиды. Таким образом,
где F — середина BC, а O — центр основания пирамиды. Таким образом, 




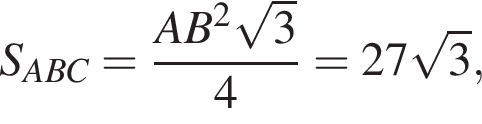
 а CO = 6.
а CO = 6.
 откуда
откуда 
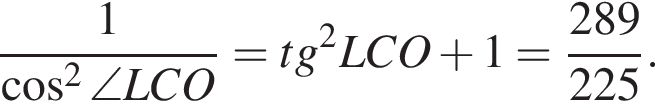





 Далее находим,
Далее находим,




 и тогда
и тогда 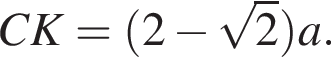 Пусть
Пусть  Из подобия треугольников MDL и KCL имеем
Из подобия треугольников MDL и KCL имеем
 Следовательно, D1NLC — параллелограмм, то есть отрезок LN параллелен отрезку CD1. Поэтому прямая DC1 перпендикулярна прямой LN и линейным углом между плоскостями MNO и DCC1 будет угол MED, где E — точка пересечения прямых DC1 и NL. Тогда
Следовательно, D1NLC — параллелограмм, то есть отрезок LN параллелен отрезку CD1. Поэтому прямая DC1 перпендикулярна прямой LN и линейным углом между плоскостями MNO и DCC1 будет угол MED, где E — точка пересечения прямых DC1 и NL. Тогда


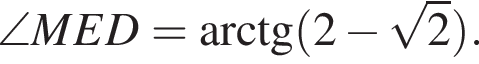

 и
и 
 Объём параллелепипеда ABCDA1B1C1D1 равен
Объём параллелепипеда ABCDA1B1C1D1 равен 

 и
и
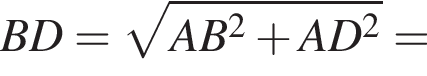
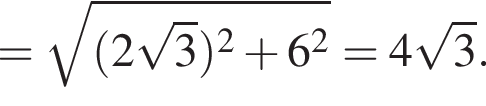




 Значит, прямая
Значит, прямая 
 следовательно, прямая
следовательно, прямая 





 значит,
значит,


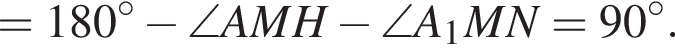


 откуда
откуда


 (только равносторонний треугольник).
(только равносторонний треугольник).
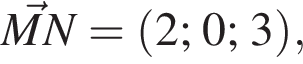




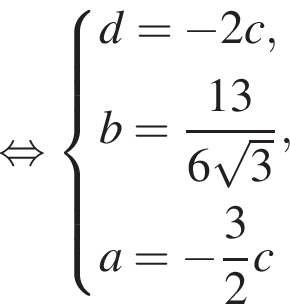








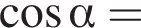


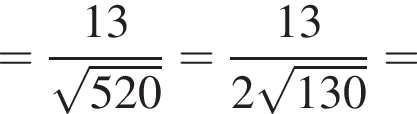

 откуда
откуда

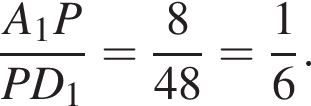



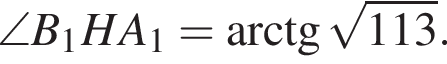








 тогда
тогда  Вектор
Вектор  тогда
тогда 
 Подставляя координаты точек B1 и K в уравнение
Подставляя координаты точек B1 и K в уравнение  плоскости α, получаем систему уравнений:
плоскости α, получаем систему уравнений:
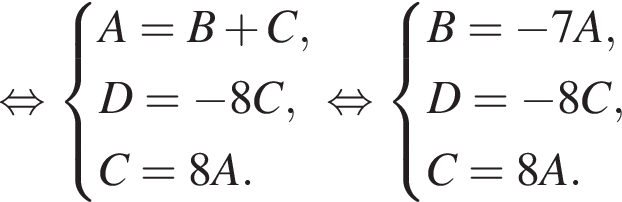



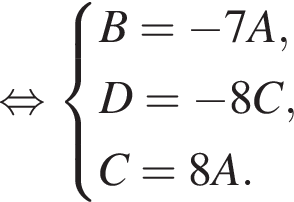

 Следовательно,
Следовательно,  а уравнение плоскости имеет вид
а уравнение плоскости имеет вид 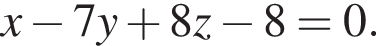
 Это равенство верно, значит, точка P принадлежит плоскости α. Следовательно,
Это равенство верно, значит, точка P принадлежит плоскости α. Следовательно, 
 получаем:
получаем:
 Далее находим, что B = C = 0. Положим
Далее находим, что B = C = 0. Положим 

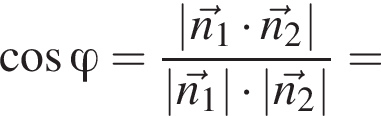


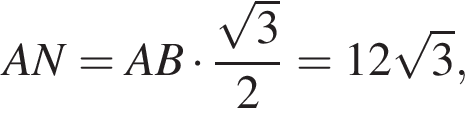


 Следовательно,
Следовательно,  По теореме косинусов для треугольника ANR:
По теореме косинусов для треугольника ANR: 














 откуда
откуда

 По теореме синусов:
По теореме синусов:








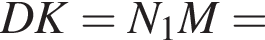



 тогда
тогда
 тогда
тогда 

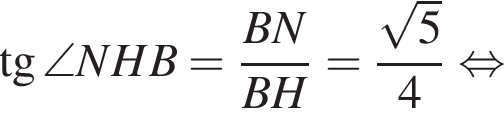








 и
и  представляют один и тот же угол.
представляют один и тот же угол.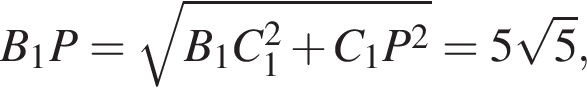

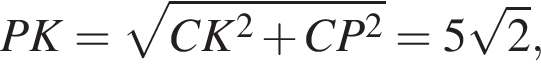





















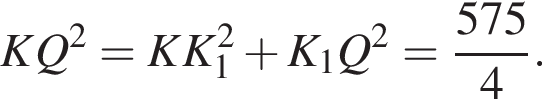








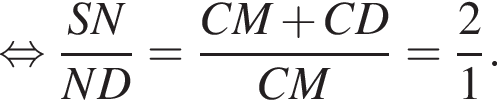









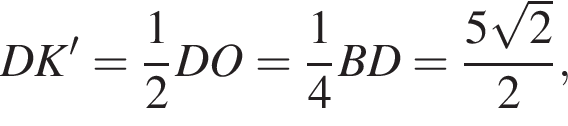






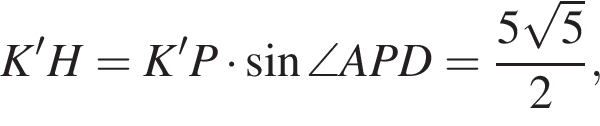







 Q — точка пересечения прямых KL и MN. Плоскости КPL и PMN перпендикулярны плоскости основания пирамиды.
Q — точка пересечения прямых KL и MN. Плоскости КPL и PMN перпендикулярны плоскости основания пирамиды.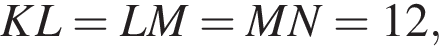 a высота пирамиды PKLMN равна 8.
a высота пирамиды PKLMN равна 8.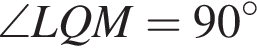 (углы KLM и LMN лежат при меньшем основании трапеции LM и являются тупыми). Каждая из плоскостей KPL и PMN содержит прямую, перпендикулярную плоскости KLM, и так как существует единственная такая прямая, проходящая через точку Q, то это прямая их пересечения — PQ. Таким образом, прямая PQ перпендикулярна плоскости KLM, следовательно, и лежащим в ней прямым KL и MN. Тем самым
(углы KLM и LMN лежат при меньшем основании трапеции LM и являются тупыми). Каждая из плоскостей KPL и PMN содержит прямую, перпендикулярную плоскости KLM, и так как существует единственная такая прямая, проходящая через точку Q, то это прямая их пересечения — PQ. Таким образом, прямая PQ перпендикулярна плоскости KLM, следовательно, и лежащим в ней прямым KL и MN. Тем самым 




 Следовательно,
Следовательно, 















 Таким образом,
Таким образом, 


 Тогда:
Тогда: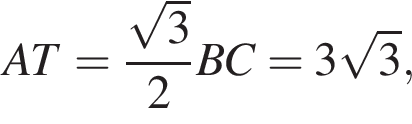





 точка K — середина ребра DD1.
точка K — середина ребра DD1. a
a 
 тогда
тогда 
 Пусть D1K = x, KD = x. По теореме Пифагора:
Пусть D1K = x, KD = x. По теореме Пифагора:

 то треугольник B1A1M — равносторонний, A1B1 = C1D1 = CD = A1M = 1. Найдем длину BD:
то треугольник B1A1M — равносторонний, A1B1 = C1D1 = CD = A1M = 1. Найдем длину BD: 


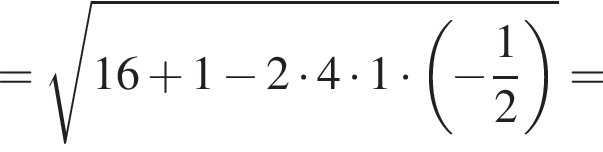



 Площадь MKCP равна, таким образом,
Площадь MKCP равна, таким образом,  равна
равна  Найдем косинус угла между плоскостью MKC и плоскостью основания:
Найдем косинус угла между плоскостью MKC и плоскостью основания:
 а
а 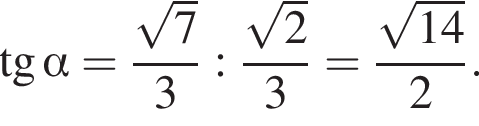

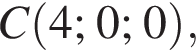
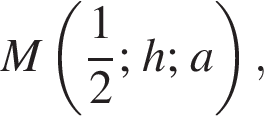



 получим:
получим:
 Вычтем из третьего уравнения системы второе и выразим С:
Вычтем из третьего уравнения системы второе и выразим С:








 Далее находим:
Далее находим:

 тогда
тогда  Выразим угол HKD:
Выразим угол HKD:
 треугольники MD1K и HDK подобны по двум углам. Имеем:
треугольники MD1K и HDK подобны по двум углам. Имеем: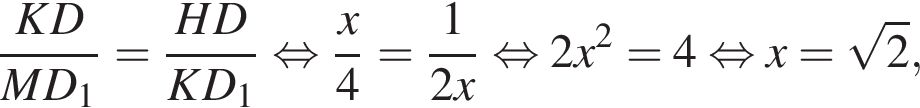









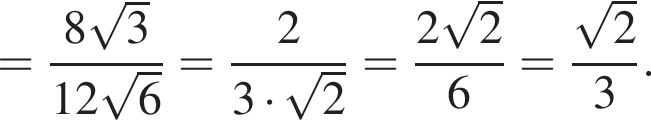



 откуда
откуда  то есть
то есть 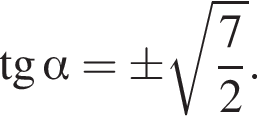 Поскольку угол острый,
Поскольку угол острый, 




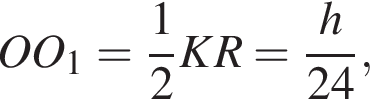
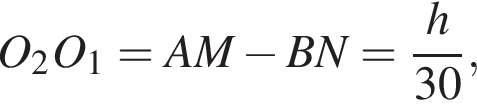


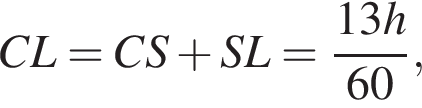










 откуда
откуда 






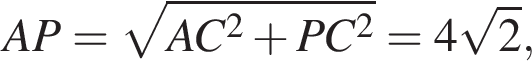

 следовательно, треугольник AKP — прямоугольный, а прямые AP и PK перпендикулярны.
следовательно, треугольник AKP — прямоугольный, а прямые AP и PK перпендикулярны.
 следовательно,
следовательно, 


 откуда
откуда 
 следовательно, по теореме Фалеса
следовательно, по теореме Фалеса  Таким образом, точки T и M совпадают.
Таким образом, точки T и M совпадают. 




 где
где 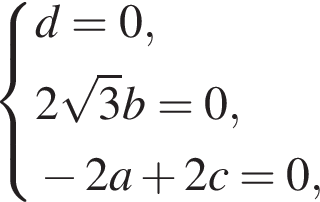
 Запишем уравнение плоскости α:
Запишем уравнение плоскости α:  где
где 
 Косинус угла между плоскостями равен модулю косинуса угла между перпендикулярными к ним векторами:
Косинус угла между плоскостями равен модулю косинуса угла между перпендикулярными к ним векторами: 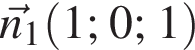 и
и  Следовательно,
Следовательно, 







 следовательно,
следовательно, 
 значит, прямая LM — средняя линия треугольника KPC, то есть точка M — середина отрезка PC. Тогда равны треугольники PB1M и CC1M, а отрезки B1M и MC1 равны как соответствующие элементы.
значит, прямая LM — средняя линия треугольника KPC, то есть точка M — середина отрезка PC. Тогда равны треугольники PB1M и CC1M, а отрезки B1M и MC1 равны как соответствующие элементы. где отрезок LH — высота трапеции. Имеем:
где отрезок LH — высота трапеции. Имеем: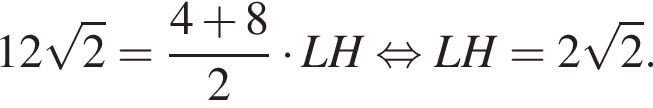
 значит, равны треугольники PBK и PBC, а тогда BK = BC и, аналогично,
значит, равны треугольники PBK и PBC, а тогда BK = BC и, аналогично,  Пусть точка O — середина отрезка KC, тогда отрезок BO — медиана и высота прямоугольного равнобедренного треугольника BKC, откуда следует
Пусть точка O — середина отрезка KC, тогда отрезок BO — медиана и высота прямоугольного равнобедренного треугольника BKC, откуда следует  Угол POB равен углу между плоскостями KLM и ABC,
Угол POB равен углу между плоскостями KLM и ABC,

 Следовательно, AE : EB = 1 : 4.
Следовательно, AE : EB = 1 : 4.
 Пусть AB = x, тогда
Пусть AB = x, тогда 
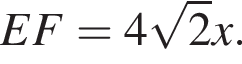 Имеем:
Имеем:
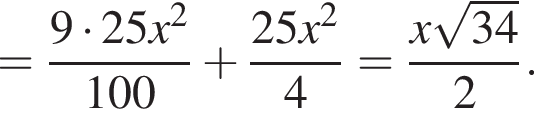





 следовательно, точка P — середина ребра SA, а точка Q — середина ребра SD. Рассмотрим сечение пирамиды, проходящее через ее высоту SH перпендикулярно прямой AD. Обозначим M и N — середины сторон BC и AD соответственно, пусть T — середина отрезка PQ, и пусть высота SH и сечение BPQC пересекаются в точке O. Из теоремы Менелая для треугольника HSN и секущей TO получаем:
следовательно, точка P — середина ребра SA, а точка Q — середина ребра SD. Рассмотрим сечение пирамиды, проходящее через ее высоту SH перпендикулярно прямой AD. Обозначим M и N — середины сторон BC и AD соответственно, пусть T — середина отрезка PQ, и пусть высота SH и сечение BPQC пересекаются в точке O. Из теоремы Менелая для треугольника HSN и секущей TO получаем:
 Следовательно, точка H — середина отрезка MN.
Следовательно, точка H — середина отрезка MN.

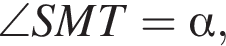 тогда:
тогда: 









 Заметим, что эта высота является также и высотой пирамиды SBPTM, проведенной из вершины S. Пусть β — угол между боковой гранью SBP и основанием BPTM. Тогда:
Заметим, что эта высота является также и высотой пирамиды SBPTM, проведенной из вершины S. Пусть β — угол между боковой гранью SBP и основанием BPTM. Тогда:

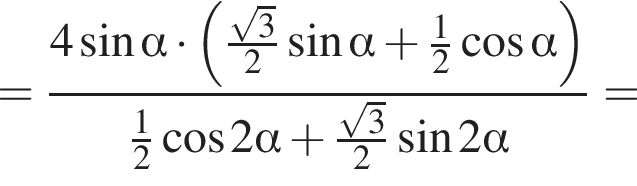









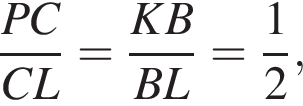 откуда
откуда  и
и  По теореме Менелая в треугольнике CSD получаем:
По теореме Менелая в треугольнике CSD получаем:



 — искомый.
— искомый. где SO — высота пирамиды. Значит, точка H — середина прямой OD, поэтому:
где SO — высота пирамиды. Значит, точка H — середина прямой OD, поэтому:




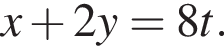 Точка H имеет координаты (9t; 9t), следовательно,
Точка H имеет координаты (9t; 9t), следовательно,






 По свойству точки пересечения медиан
По свойству точки пересечения медиан  а тогда
а тогда  откуда следует параллельность отрезков MK и DS. Плоскость
откуда следует параллельность отрезков MK и DS. Плоскость 



 Здесь мы использовали, что
Здесь мы использовали, что



 Подставив координаты соответствующих точек, получим:
Подставив координаты соответствующих точек, получим:





 Уравнение плоскости имеет вид
Уравнение плоскости имеет вид 
 Плоскость
Плоскость  Найдем косинус угла между плоскостями:
Найдем косинус угла между плоскостями:























 то есть
то есть 
 Значит,
Значит,







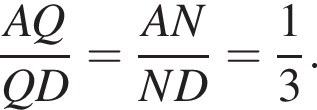 Тогда по теореме Менелая для треугольника FAP и секущей NQ получаем:
Тогда по теореме Менелая для треугольника FAP и секущей NQ получаем:




 откуда
откуда  По теореме Менелая для треугольника ASF и секущей XY получаем:
По теореме Менелая для треугольника ASF и секущей XY получаем: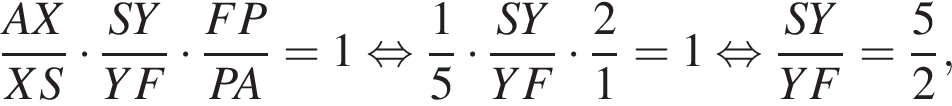
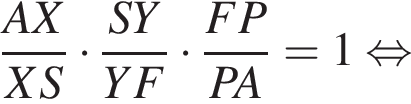

 Площади треугольников SXY и SAF с общим углом S относятся как произведения сторон, заключающих этот угол:
Площади треугольников SXY и SAF с общим углом S относятся как произведения сторон, заключающих этот угол:

 Положим AB = 3a, SA = 6a, тогда по теореме Пифагора
Положим AB = 3a, SA = 6a, тогда по теореме Пифагора  а тогда
а тогда  Далее,
Далее, 

 По теореме косинусов:
По теореме косинусов:


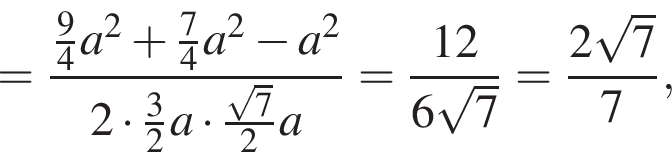




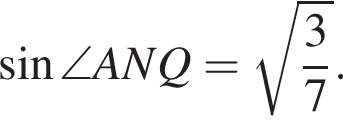 Тогда
Тогда  и
и  где R — проекция точки H на отрезок NQ (см. рис.).
где R — проекция точки H на отрезок NQ (см. рис.).
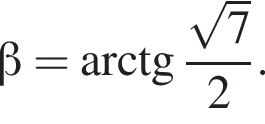

 AD = 12, AA1 = 16.
AD = 12, AA1 = 16. (из результатов пункта а) следует, что K — середина EA1). Теперь, вычисляя двумя способами площадь треугольника EFA1, получим A1H · EF = A1E · FK, то есть
(из результатов пункта а) следует, что K — середина EA1). Теперь, вычисляя двумя способами площадь треугольника EFA1, получим A1H · EF = A1E · FK, то есть 


 тогда
тогда 

 Четырехугольник MNPK — параллелограмм по определению, поэтому отрезки NK и MP имеют общую точку O. Пусть h — расстояние от точки O до плоскости основания. Тогда
Четырехугольник MNPK — параллелограмм по определению, поэтому отрезки NK и MP имеют общую точку O. Пусть h — расстояние от точки O до плоскости основания. Тогда  а кроме того,
а кроме того,
 Следовательно,
Следовательно, 
 Из условия
Из условия 
 тогда по теореме Пифагора
тогда по теореме Пифагора















 и
и  По теореме Менелая для треугольника AOD и прямой KL:
По теореме Менелая для треугольника AOD и прямой KL:


 тогда:
тогда:
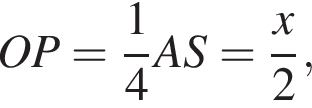


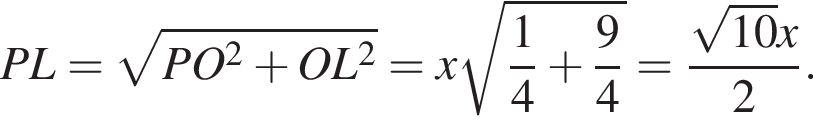


 то
то











 —
—















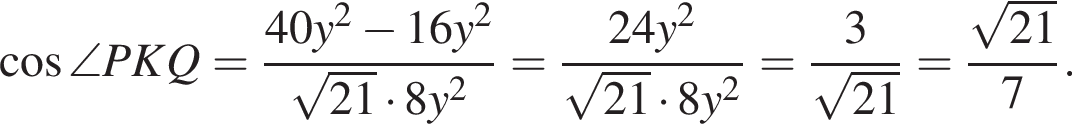


 Следовательно, площадь трапеции равна
Следовательно, площадь трапеции равна









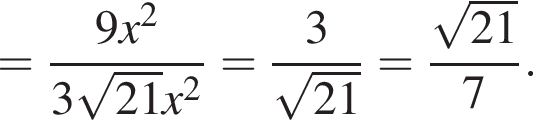
 Пусть также
Пусть также  а потому
а потому  и
и  Из прямоугольных треугольников
Из прямоугольных треугольников 
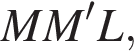 LKB и NMB1 соответственно получаем:
LKB и NMB1 соответственно получаем:







 тогда в трапеции KLMN равны высоты:
тогда в трапеции KLMN равны высоты:






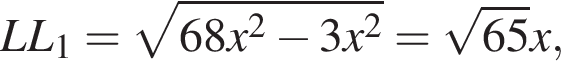
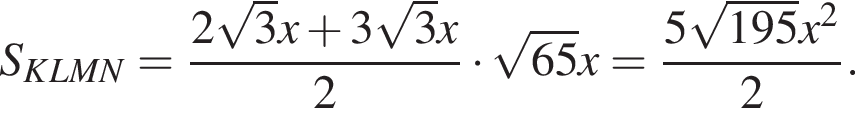






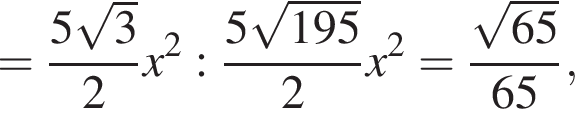





 Следовательно, четырехугольник EFTD1 — трапеция.
Следовательно, четырехугольник EFTD1 — трапеция. 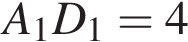 и
и  Гипотенуза D1M равна
Гипотенуза D1M равна  Значит, высота A1H треугольника, проведённая к гипотенузе, равна
Значит, высота A1H треугольника, проведённая к гипотенузе, равна