1. Тип 13 № 507886 

Классификатор алгебры: Уравнения, рациональные относительно тригонометрических функций
Методы алгебры: Формулы приведения
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
Уравнения. Тригонометрические уравнения, разные задачи
i
а) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие отрезку 
Решение. а) Преобразуем уравнение:









б) Отберем корни на промежутке 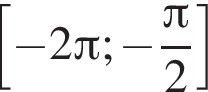 с помощью тригонометрической окружности. Получаем
с помощью тригонометрической окружности. Получаем  и
и 
Ответ: а)  б)
б) 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Ответ: а)  б)
б) 
 б)
б) 
507886
а)  б)
б) 
 б)
б) 
Классификатор алгебры: Уравнения, рациональные относительно тригонометрических функций
Методы алгебры: Формулы приведения
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения



 откуда
откуда  или
или  откуда
откуда 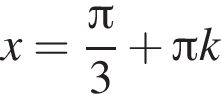 или
или 

 б)
б) 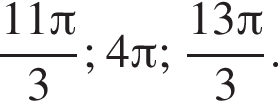





 откуда
откуда  либо
либо  откуда
откуда 
 поэтому из корней квадратного уравнения заданному отрезку принадлежит число
поэтому из корней квадратного уравнения заданному отрезку принадлежит число 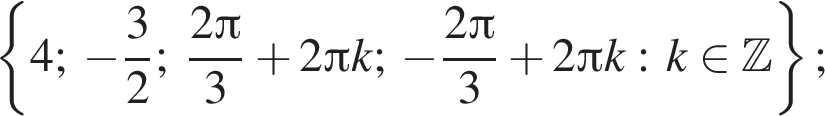 б)
б) 


 Значит,
Значит,  или
или  где
где  во втором случае
во втором случае  где
где  принадлежат корни
принадлежат корни  б)
б) 







 поэтому при таких k решений на отрезке [3; 5] нет.
поэтому при таких k решений на отрезке [3; 5] нет. Заметим, что
Заметим, что  поэтому корень
поэтому корень  поэтому при таких k решений на отрезке [3; 5] нет.
поэтому при таких k решений на отрезке [3; 5] нет. б)
б) 










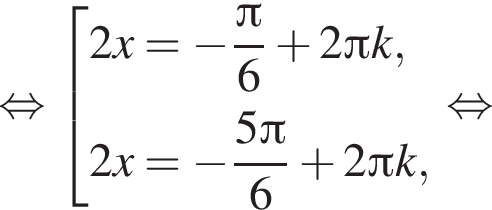
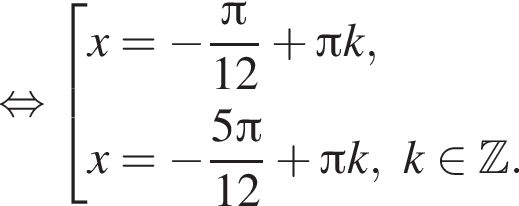

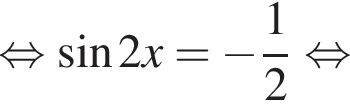

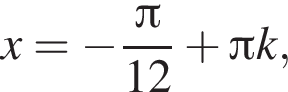
 где
где  где
где 






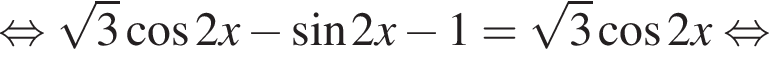





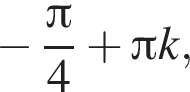 где
где 

 формулу приведения
формулу приведения  и формулу синуса суммы:
и формулу синуса суммы: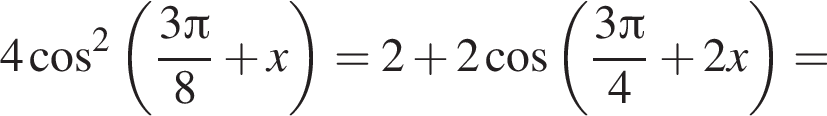
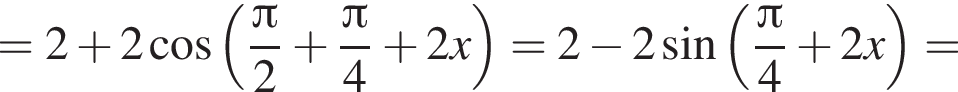




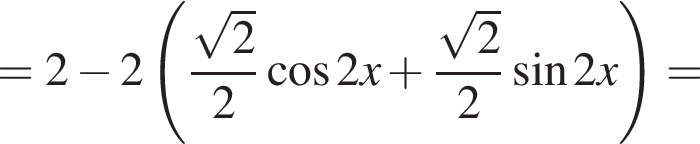





 б)
б) 

 Из неё следует, что
Из неё следует, что 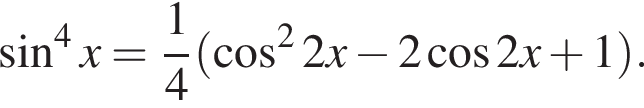 Поэтому из исходного уравнения получаем:
Поэтому из исходного уравнения получаем:


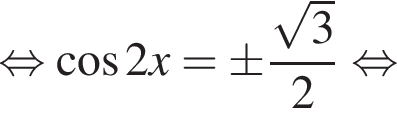



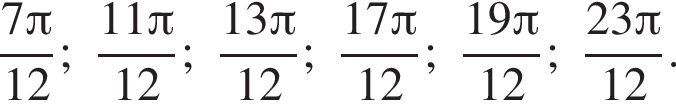
 б)
б) 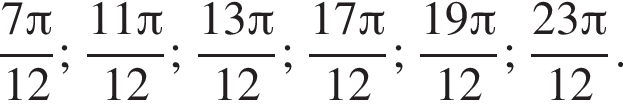










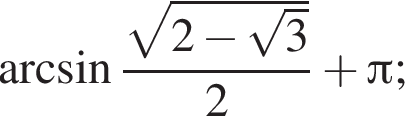



 б)
б) 

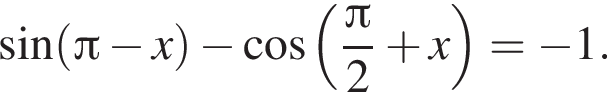









 б)
б) 
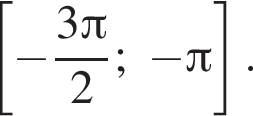



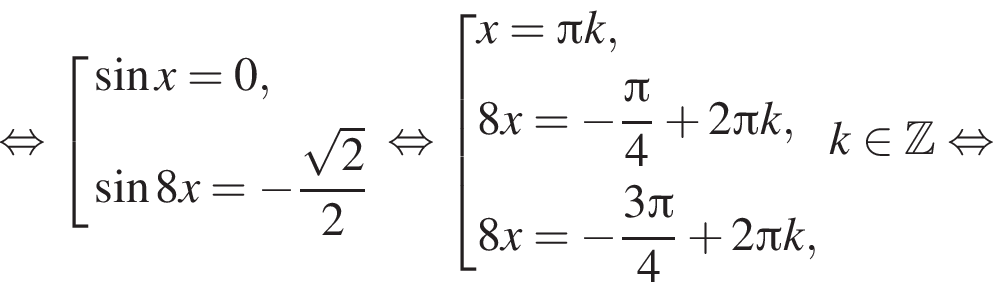


















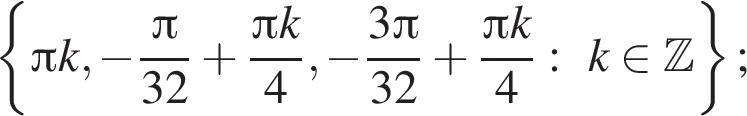 б)
б) 







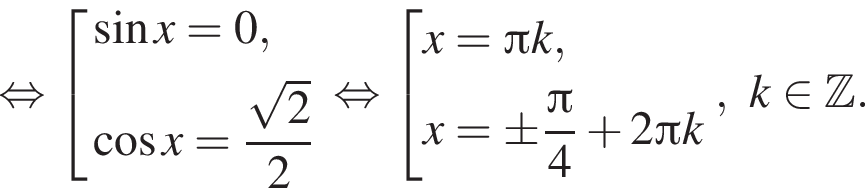


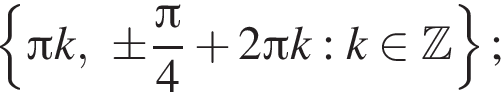 б)
б) 

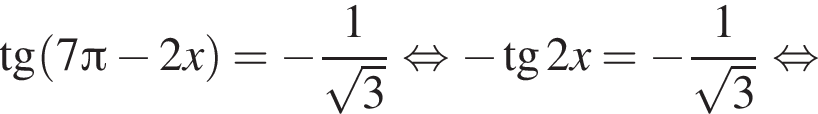







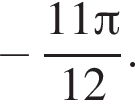
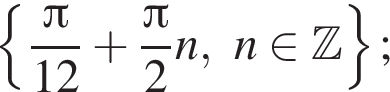 б)
б) 

 тогда:
тогда: 



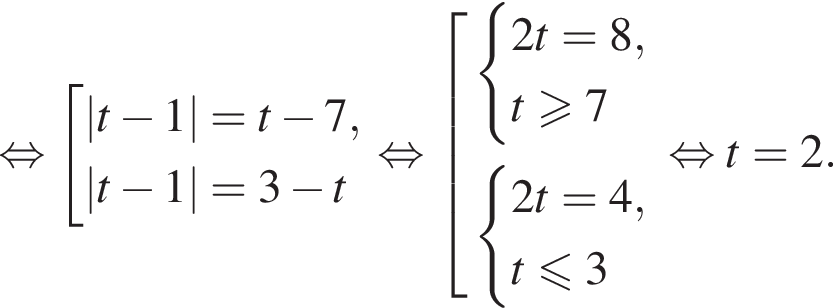
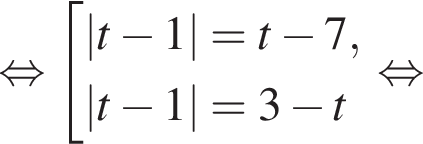

 откуда
откуда 
 б)
б)  удобно решить, используя геометрический смысл модуля. Действительно, с геометрической точки зрения левая часть уравнения представляет собой разность расстояний от точки с координатой t до точек с координатами
удобно решить, используя геометрический смысл модуля. Действительно, с геометрической точки зрения левая часть уравнения представляет собой разность расстояний от точки с координатой t до точек с координатами 

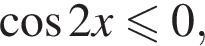 тогда это эквивалентно совокупности:
тогда это эквивалентно совокупности:






 б)
б) 

 :
: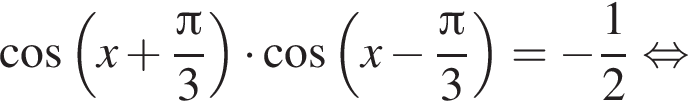







 б)
б) 
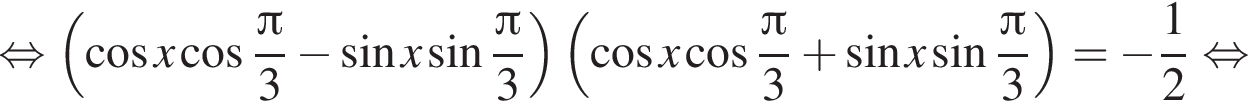














 и
и  Поэтому последнее равенство может достигаться только в случае, если
Поэтому последнее равенство может достигаться только в случае, если  а
а  Решим систему уравнений:
Решим систему уравнений:



 получим
получим  Следовательно,
Следовательно, 







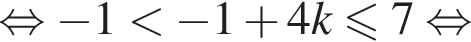
 б)
б) 
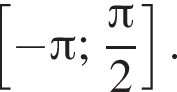




 С помощью числовой окружности отберём корни, принадлежащие отрезку
С помощью числовой окружности отберём корни, принадлежащие отрезку 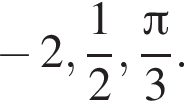
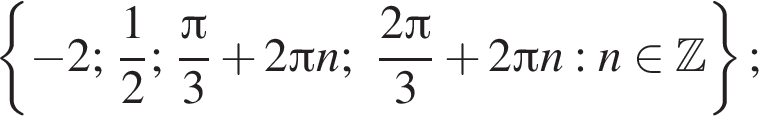 б)
б) 




 получим
получим  Условию
Условию  соответствует только
соответствует только 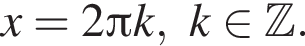
 получим
получим







 б)
б) 









 б)
б) 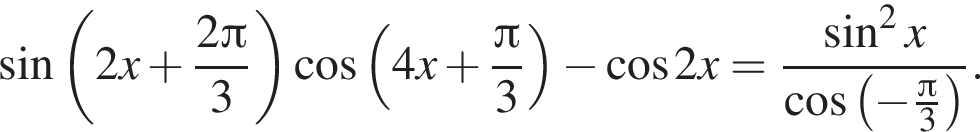



 или
или 

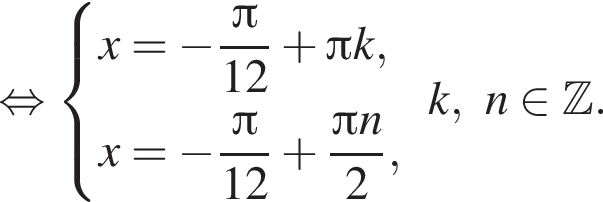









 б)
б) 






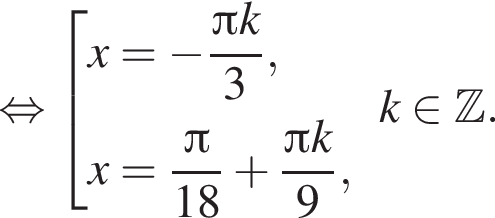

 методом неравенств:
методом неравенств: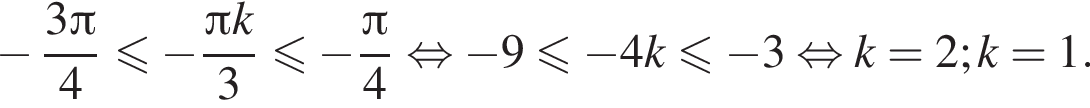




 и
и 





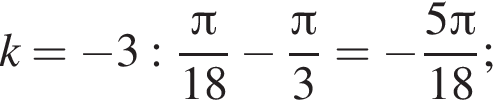




 где
где 







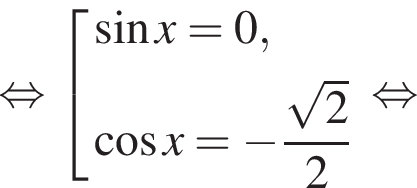
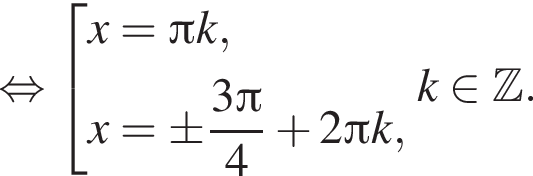
 Получим числа:
Получим числа:  б)
б) 




 Для второго уравнения сделаем замену
Для второго уравнения сделаем замену  получим уравнение
получим уравнение  Его дискриминант равен нулю:
Его дискриминант равен нулю: 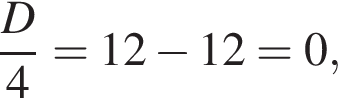 тогда
тогда  Сделав обратную замену, получаем
Сделав обратную замену, получаем
 б)
б) 




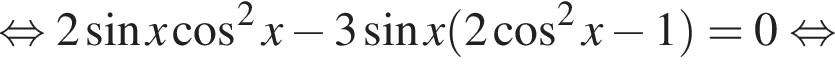







 б)
б) 
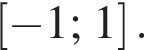
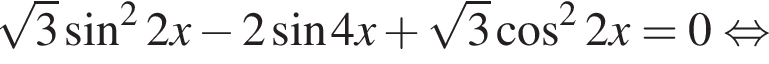








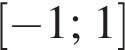 лежат корни при k = 0:
лежат корни при k = 0:  б)
б) 

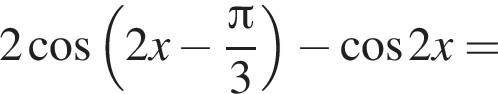

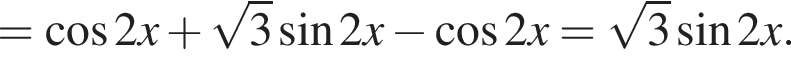











 б)
б) 







 б)
б) 












 б)
б) 
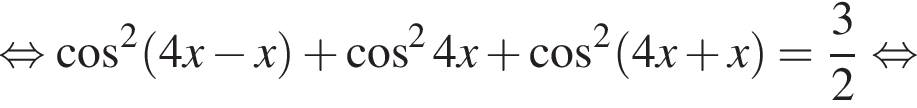






















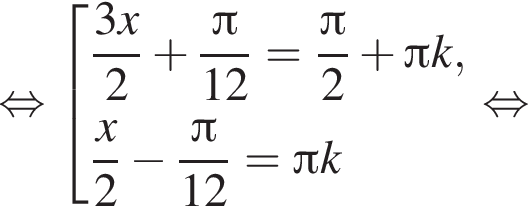




 б)
б) 







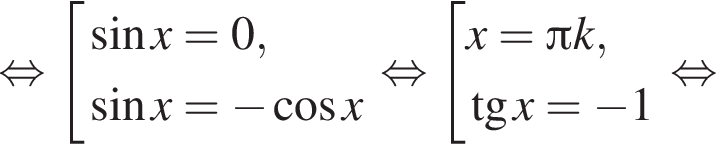



 б)
б) 







 б)
б) 
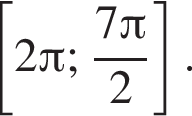


 откуда
откуда 
 откуда
откуда 


 Получим числа:
Получим числа:  б)
б) 
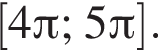
 тогда
тогда





 с помощью двойного неравенства:
с помощью двойного неравенства:
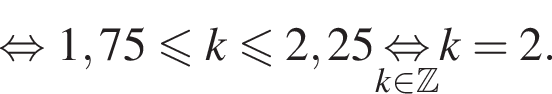



 б)
б) 

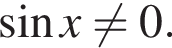 Преобразуем уравнение при этом условии:
Преобразуем уравнение при этом условии:










 не обращается в нуль, поскольку косинус и синус одного угла одновременно в нуль не обращаются.
не обращается в нуль, поскольку косинус и синус одного угла одновременно в нуль не обращаются.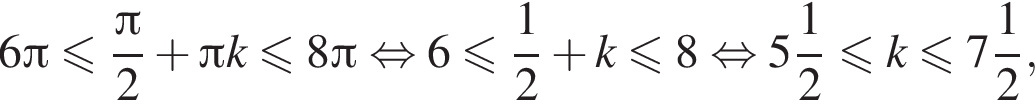




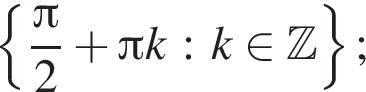 б)
б) 








 тогда
тогда



















 :
: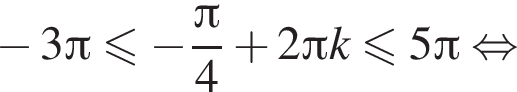







 б)
б)  и
и  Можно было бы поступить несколько иначе, обозначив
Можно было бы поступить несколько иначе, обозначив  Приведем такое решение, для этого возведем обе части уравнения
Приведем такое решение, для этого возведем обе части уравнения

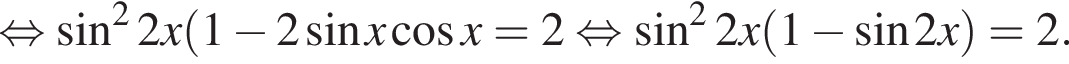


 тогда
тогда












 являются решениями уравнения. При нечетных значениях k, используя периодичность и применяя формулы приведения, имеем:
являются решениями уравнения. При нечетных значениях k, используя периодичность и применяя формулы приведения, имеем: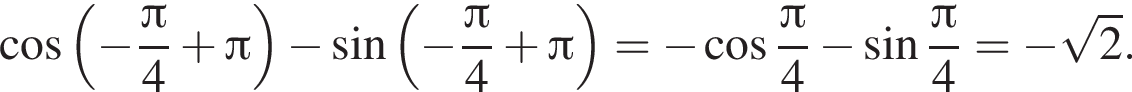


 являются посторонними корнями.
являются посторонними корнями.








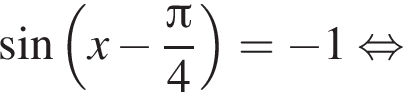














 дает все решения уравнения.
дает все решения уравнения.





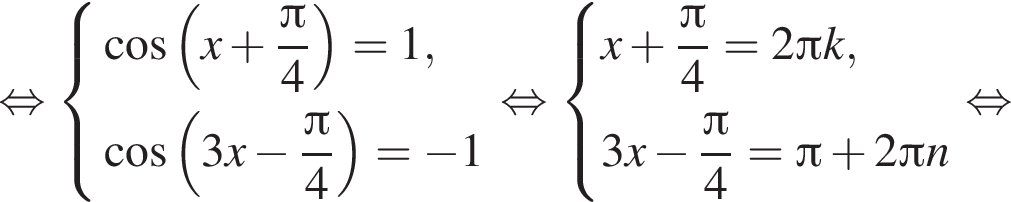






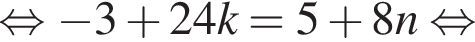




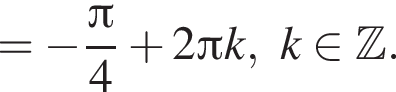









 решений не имеет, поскольку синус и косинус одного аргумента не обращаются в −1 одновременно.
решений не имеет, поскольку синус и косинус одного аргумента не обращаются в −1 одновременно.


 б)
б) 












 то получаем, что
то получаем, что  Обоим этим условиям одновременно удовлетворяют лишь числа
Обоим этим условиям одновременно удовлетворяют лишь числа  откуда
откуда 
 то получаем, что
то получаем, что  Этим условиям одновременно удовлетворяют числа
Этим условиям одновременно удовлетворяют числа  а значит,
а значит, 
 отберем при помощи двойных неравенств:
отберем при помощи двойных неравенств:

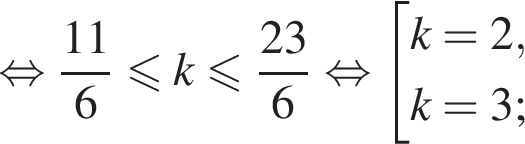

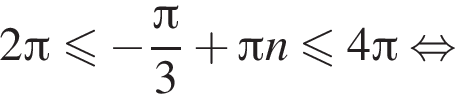

 б)
б) 





 б)
б) 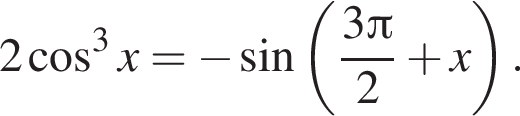




 откуда следует, что
откуда следует, что 
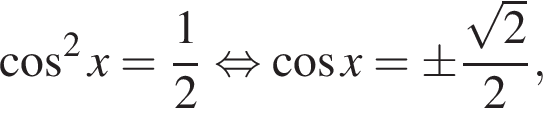




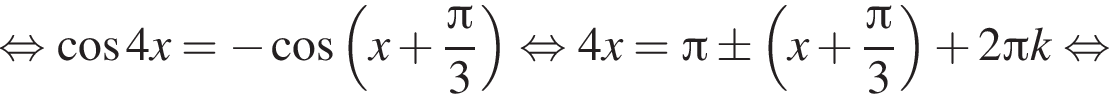




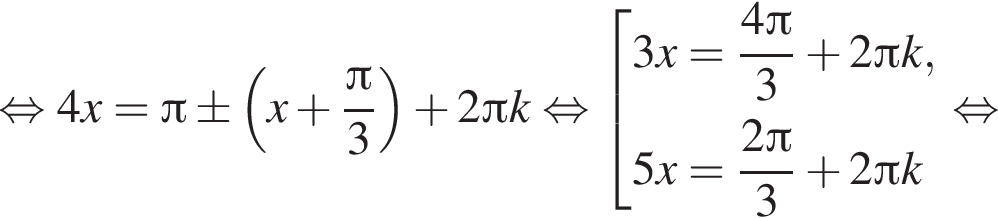








 Далее,
Далее, 
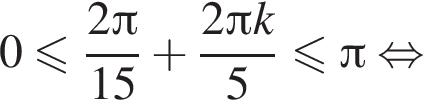

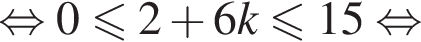




 Подставляя, получаем:
Подставляя, получаем:




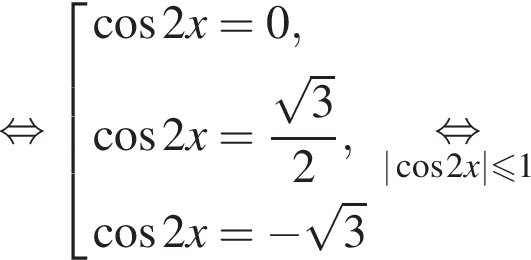

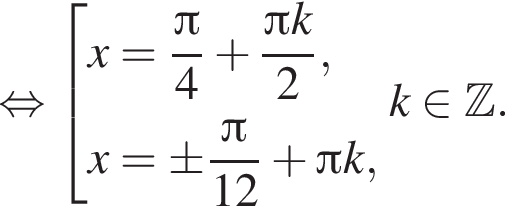


 при помощи тригонометрической окружности (см. рис.). Получим числа:
при помощи тригонометрической окружности (см. рис.). Получим числа: 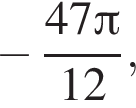



















 б)
б) 










 б)
б) 








 с помощью тригонометрической окружности. Получаем числа:
с помощью тригонометрической окружности. Получаем числа:  б)
б) 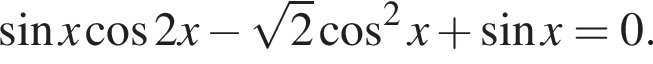
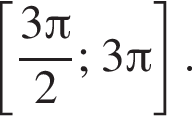







 с помощью тригонометрической окружности. Получаем числа:
с помощью тригонометрической окружности. Получаем числа:  б)
б) 






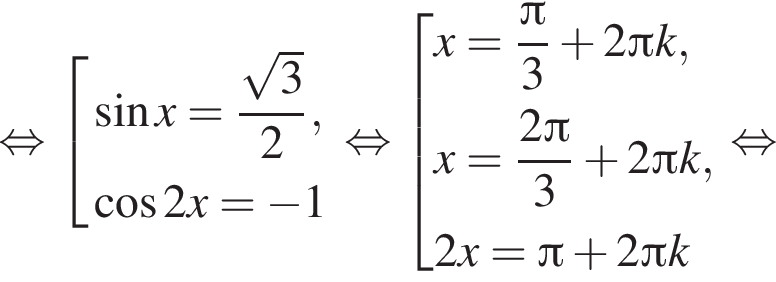



 при помощи тригонометрической окружности. Подходят:
при помощи тригонометрической окружности. Подходят:  б)
б) 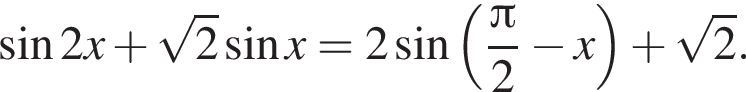






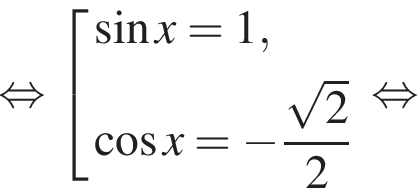

 б)
б) 







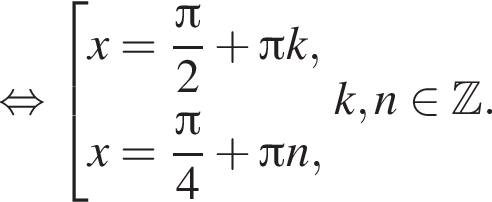







 б)
б) 










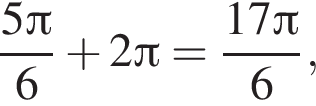 он лежит в отрезке. Значению
он лежит в отрезке. Значению 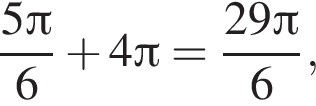 он лежит в отрезке. При
он лежит в отрезке. При  а потому они лежат правее отрезка
а потому они лежат правее отрезка  б)
б) 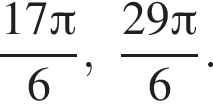









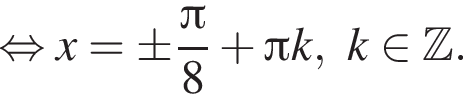


 б)
б) 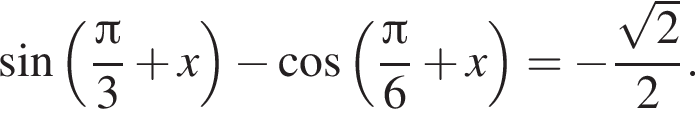


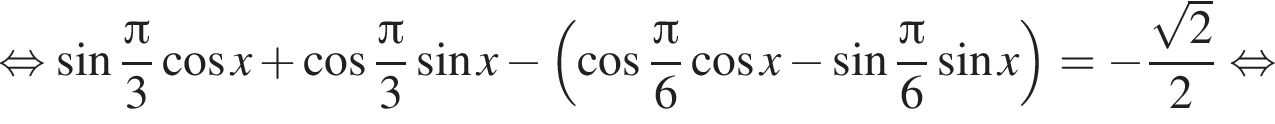
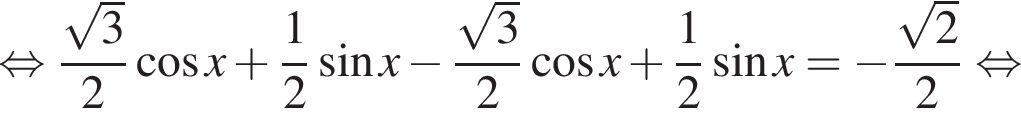


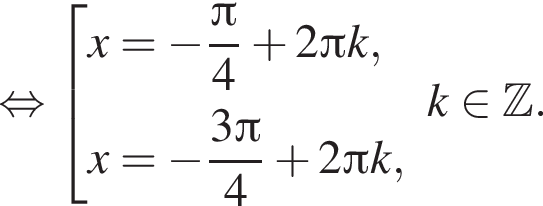
 на тригонометрической окружности. Получаем:
на тригонометрической окружности. Получаем:  б)
б) 

 Поэтому при условии
Поэтому при условии  то есть если
то есть если  уравнение принимает вид
уравнение принимает вид

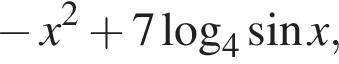





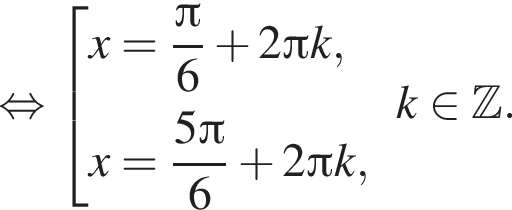
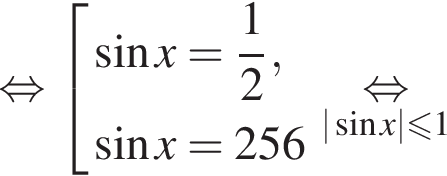

 попадают корни
попадают корни  лежит число
лежит число  б)
б) 










 где параметр k пробегает множество целых чисел.
где параметр k пробегает множество целых чисел.  при помощи двойного неравенства. Находим:
при помощи двойного неравенства. Находим: 


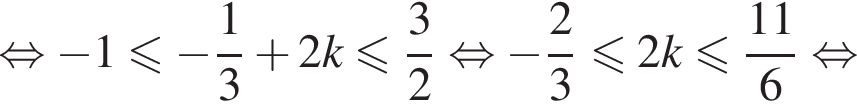



 б)
б) 







 б) 0,
б) 0, 










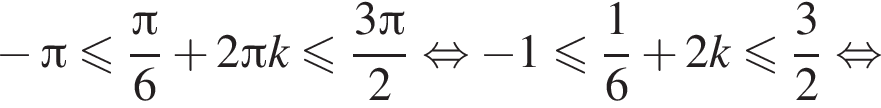






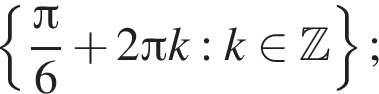

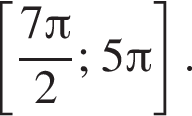


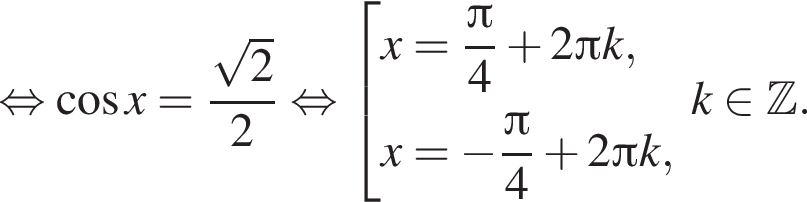




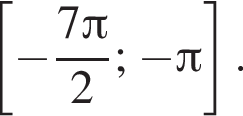










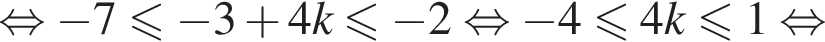
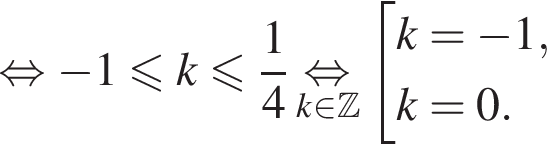


















 и
и 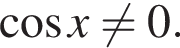 Для таких значений x можно умножить обе части уравнения на
Для таких значений x можно умножить обе части уравнения на 








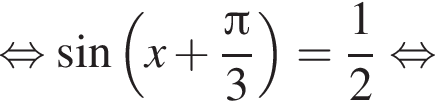

 не входит в ОДЗ уравнения.
не входит в ОДЗ уравнения.