1. Тип Д13 C3 № 505588 

Классификатор алгебры: Системы неравенств
Методы алгебры: Выделение целой части дроби
Кодификатор ФИПИ/Решу ЕГЭ:
Системы сложных неравенств. Рациональные, иррациональные, показательные неравенства
i
Решите систему неравенств 
Решение. Решим второе неравенство системы:

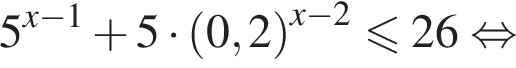
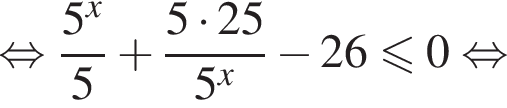



Рассмотрим первое неравенство системы на множестве [1; 3]. Преобразуем его правую часть:









Получаем:







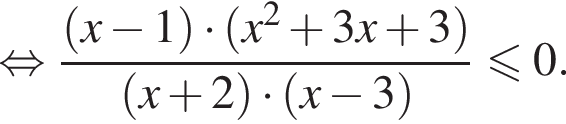
Квадратный трехчлен  при всех
при всех ![]() поскольку
поскольку 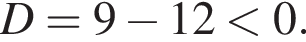 Кроме того, на [1; 3]
Кроме того, на [1; 3] 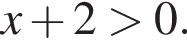 Следовательно:
Следовательно:



Ответ: ![]()
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ. | 3 |
| Обоснованно получены верные ответы в обоих неравенствах исходной системы. | 2 |
| Обоснованно получен верный ответ в одном неравенстве исходной системы. ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения системы неравенств. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 3 |
Ответ: 
505588
Классификатор алгебры: Системы неравенств
Методы алгебры: Выделение целой части дроби
Кодификатор ФИПИ/Решу ЕГЭ:



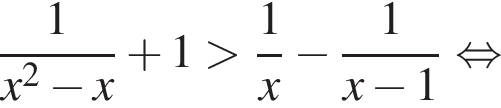


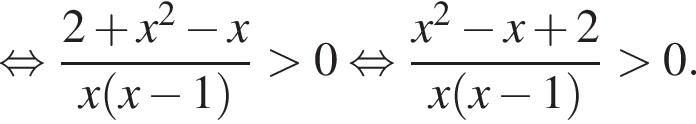


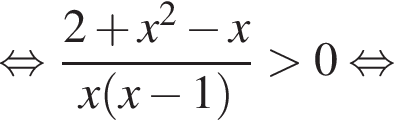

 при всех
при всех 



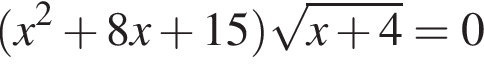 будут числа: −4 и −3. (Корень квадратного трехчлена
будут числа: −4 и −3. (Корень квадратного трехчлена  равный −5 не может служить искомым корнем из-за неотрицательности выражения
равный −5 не может служить искомым корнем из-за неотрицательности выражения 
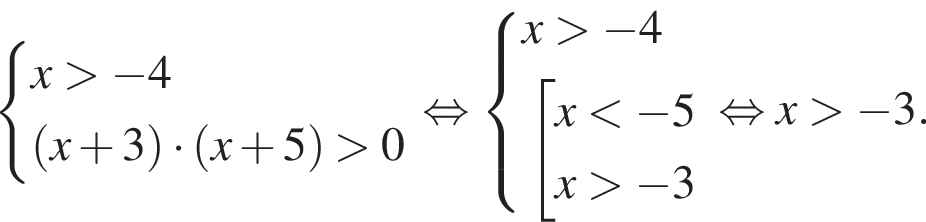


 Пересечением решений обоих неравенств будет множество
Пересечением решений обоих неравенств будет множество 








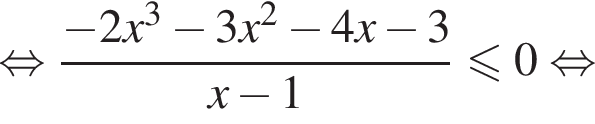



 для любого
для любого  Следовательно,
Следовательно, 



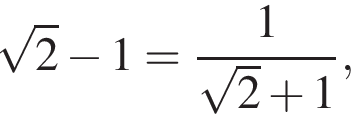 поскольку
поскольку 
 тогда:
тогда:





 Решения второго неравенства — множество
Решения второго неравенства — множество 






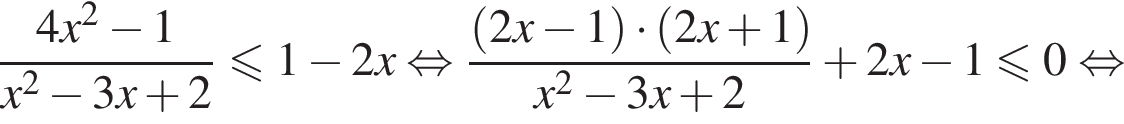





 для любого
для любого  Кроме того, на рассматриваемом множестве также
Кроме того, на рассматриваемом множестве также 


 Тогда рассматриваемое неравенство можно представить системой:
Тогда рассматриваемое неравенство можно представить системой: 


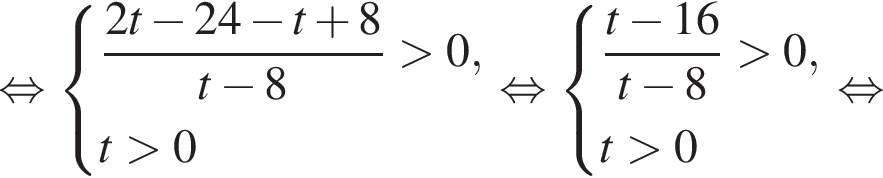


















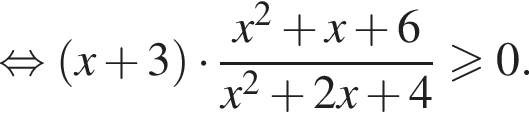
 поскольку дискриминанты квадратных трехчленов (левые части неравенств) отрицательны. Следовательно,
поскольку дискриминанты квадратных трехчленов (левые части неравенств) отрицательны. Следовательно, 
 Теперь с учетом ограничений на значения
Теперь с учетом ограничений на значения  и решений первого неравенства системы рассмотрим второе неравенство только на множестве
и решений первого неравенства системы рассмотрим второе неравенство только на множестве  Очевидно, что на этом множестве:
Очевидно, что на этом множестве:
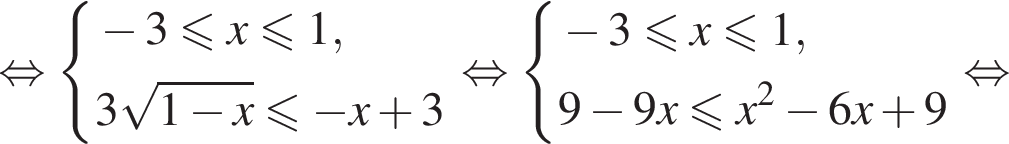


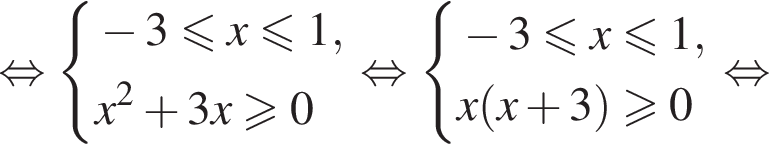






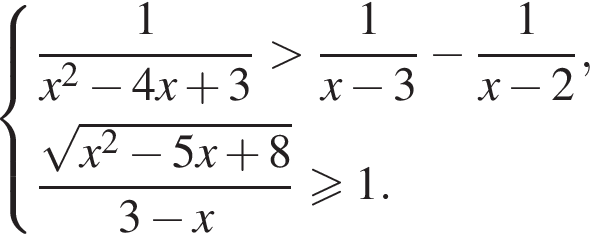
 А для того чтобы левая часть неравенства была не меньше 1, необходимо и достаточно выполнение двух условий:
А для того чтобы левая часть неравенства была не меньше 1, необходимо и достаточно выполнение двух условий:  и
и  Решим систему:
Решим систему: 
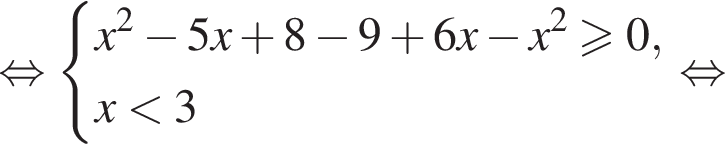


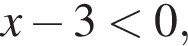 то
то 


 А также на
А также на  Значит, на этом множестве
Значит, на этом множестве 










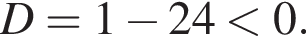 Следовательно,
Следовательно, 
















 Следовательно,
Следовательно, 






 имеем, что
имеем, что 

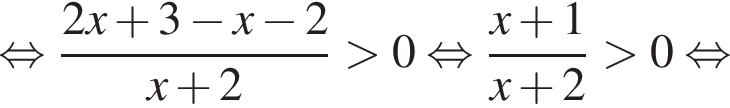



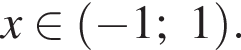 Итак, решения исходной системы:
Итак, решения исходной системы: 

 Итак, решения первого неравенства есть множество
Итак, решения первого неравенства есть множество 
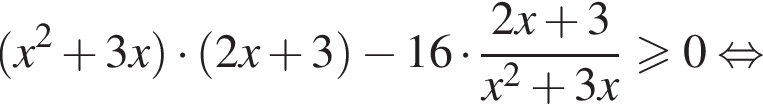




 для всех
для всех 


 будем иметь:
будем иметь:  значит,
значит, 






 Тогда:
Тогда: 

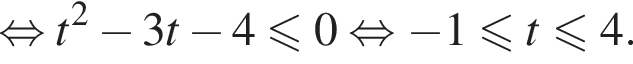





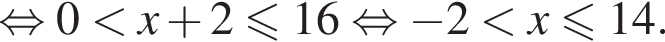



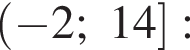




















 число 3 не входит в искомые решения:
число 3 не входит в искомые решения:


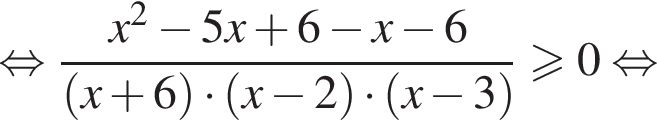




 то на множестве
то на множестве 







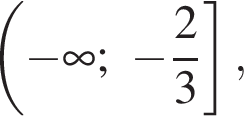

 так как в точках
так как в точках  Тогда
Тогда  неравенство примет вид:
неравенство примет вид: или
или 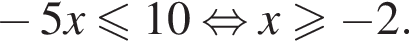

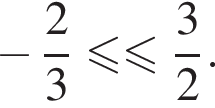 Тогда
Тогда 
 неравенство примет вид:
неравенство примет вид: 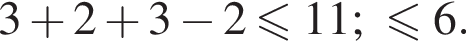 На рассматриваемом промежутке получим другую часть искомых решений:
На рассматриваемом промежутке получим другую часть искомых решений: 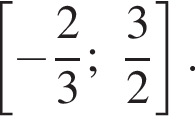
 Тогда
Тогда 
 неравенство примет вид:
неравенство примет вид:












 то на этом множестве
то на этом множестве  Далее имеем:
Далее имеем:





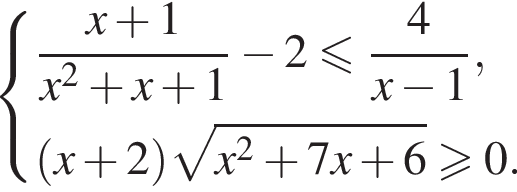




 являются числа: −1 и −3.
являются числа: −1 и −3.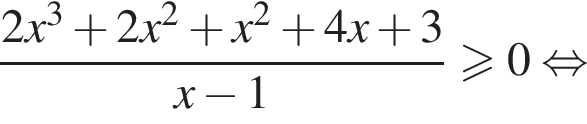



 Теперь решим второе неравенство системы.
Теперь решим второе неравенство системы. 
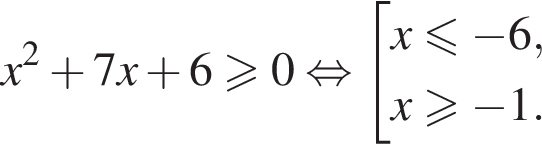

 Пересечением решений обоих неравенств будет множество
Пересечением решений обоих неравенств будет множество 

 Тогда:
Тогда: 



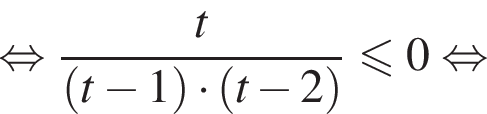






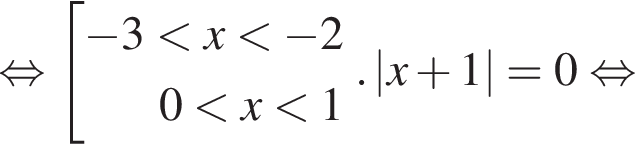


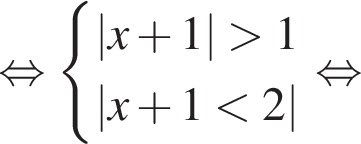


 то
то  и второе неравенство примет вид:
и второе неравенство примет вид:





 или
или 
 Следовательно, на рассматриваемом множестве
Следовательно, на рассматриваемом множестве 
 то
то и второе неравенство системы примет вид:
и второе неравенство системы примет вид:



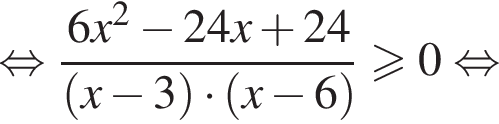







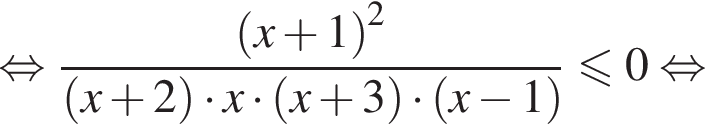










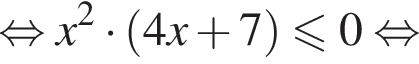




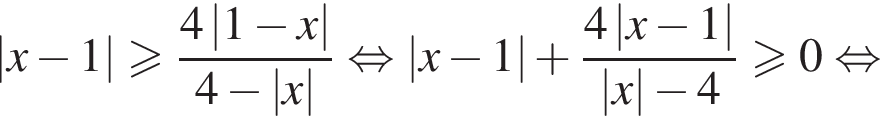
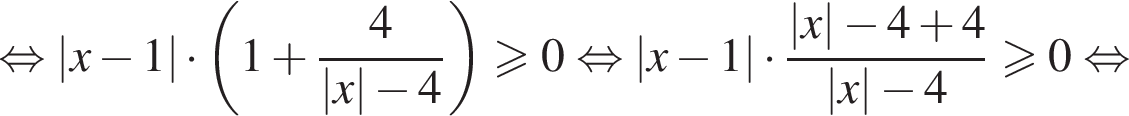
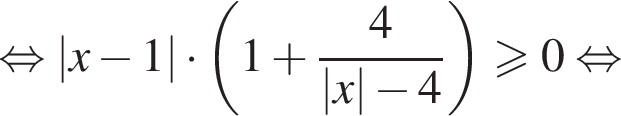


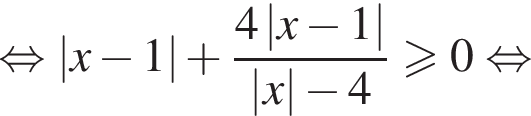
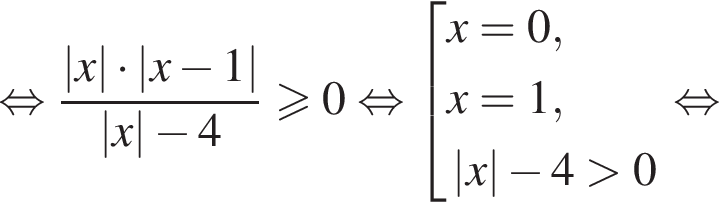

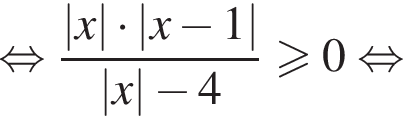

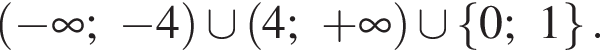 Пересечение решений обоих неравенств системы есть множество
Пересечение решений обоих неравенств системы есть множество 





 левая часть последнего неравенства неположительна, тогда как правая ее часть неотрицательна. Следовательно, неравенство выполняется при любом
левая часть последнего неравенства неположительна, тогда как правая ее часть неотрицательна. Следовательно, неравенство выполняется при любом  Значит,
Значит,  есть часть решений этого неравенства.
есть часть решений этого неравенства. 



 при любом
при любом 



 на два подмножества:
на два подмножества:  и
и  и на каждом из них рассмотрим второе неравенство системы. Ясно, что на каждом из них
и на каждом из них рассмотрим второе неравенство системы. Ясно, что на каждом из них 
 значит,
значит,  Тогда рассматриваемое неравенство имеет вид:
Тогда рассматриваемое неравенство имеет вид: 
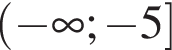 решениями второго неравенства системы будет его подмножество
решениями второго неравенства системы будет его подмножество 


 Последнее неравенство от значений переменной не зависит, следовательно,
Последнее неравенство от значений переменной не зависит, следовательно, 

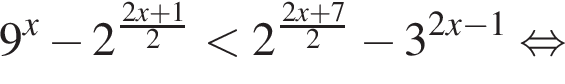
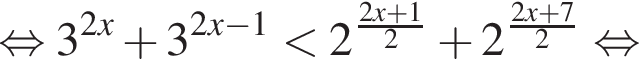





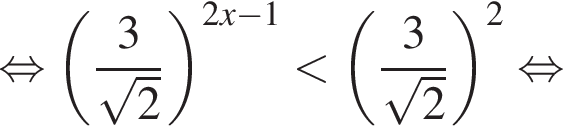


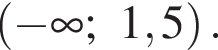


 или
или 


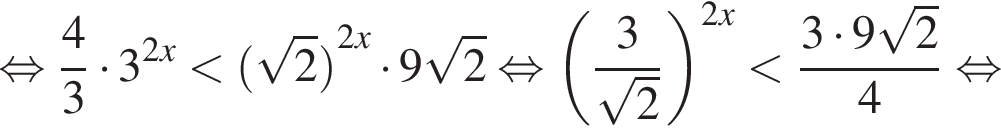







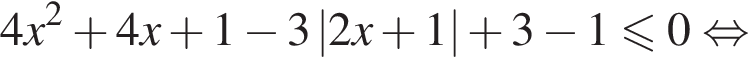





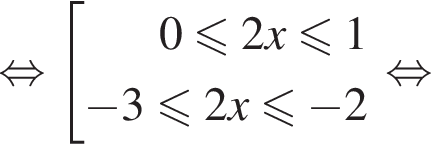
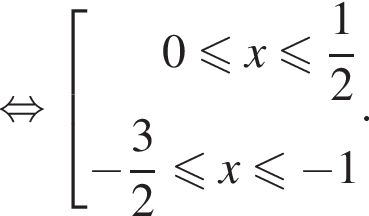

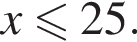
 Поэтому
Поэтому 
 для всех
для всех  Следовательно, второе неравенство на промежутке
Следовательно, второе неравенство на промежутке  равносильно неравенству
равносильно неравенству 









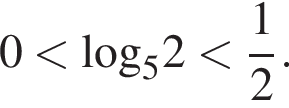 Действительно,
Действительно, 
 (неравенство очевидное).
(неравенство очевидное). 
 относительно
относительно  использована теорема Виета.
использована теорема Виета.
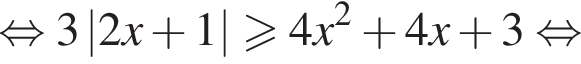






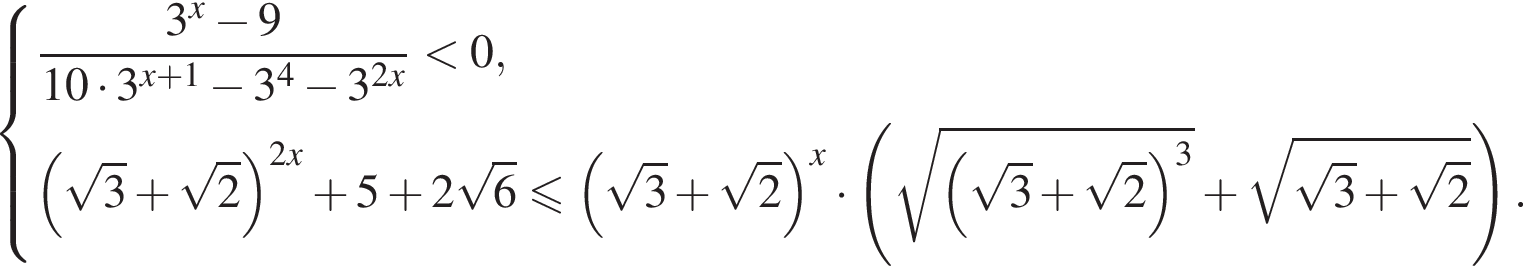



 относительно
относительно 







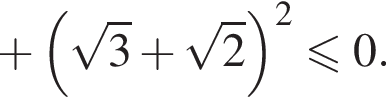


 Тогда при
Тогда при 








 на
на  поскольку их множества решений совпадают на
поскольку их множества решений совпадают на 

 меньше нуля (
меньше нуля ( ). Следовательно, решение этой системы совпадет с решением неравенства
). Следовательно, решение этой системы совпадет с решением неравенства 



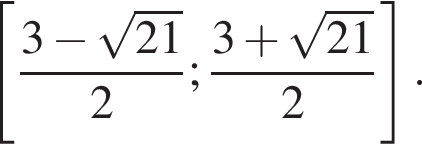

 Значит,
Значит, 




 Докажем это:
Докажем это: 


 что равносильно цепочке неравенств
что равносильно цепочке неравенств  Последнее неравенство выполнимо только при
Последнее неравенство выполнимо только при  Но значение
Но значение 

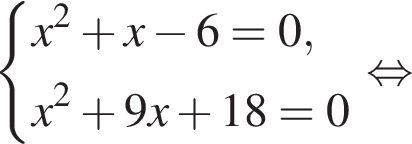



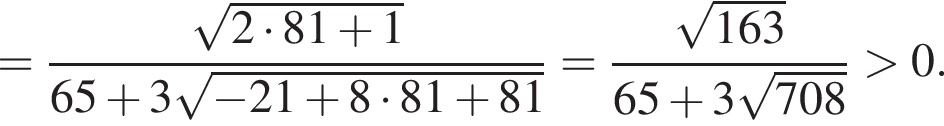

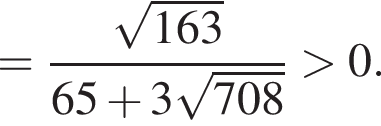
 первое неравенство заданной системы обращается в верное числовое неравенство.
первое неравенство заданной системы обращается в верное числовое неравенство.
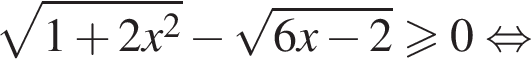






 Действительно,
Действительно, 

 (неравенство верно).
(неравенство верно).







 с числами
с числами  и
и 








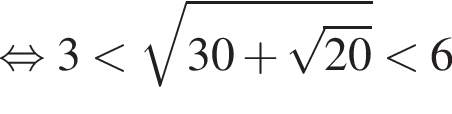


 (неравенство очевидное).
(неравенство очевидное).

 использована замена выражения
использована замена выражения  на выражение
на выражение  с учетом ограничений на значения
с учетом ограничений на значения 
 Разобъем числовую прямую на промежутки:
Разобъем числовую прямую на промежутки: 


 и определим знаки подмодульных выражений на каждом из этих промежутков.
и определим знаки подмодульных выражений на каждом из этих промежутков. Тогда все подмодульные выражения будут неположительными. Неравенство примет вид:
Тогда все подмодульные выражения будут неположительными. Неравенство примет вид: 



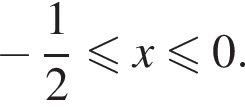 Тогда
Тогда 



 Тогда
Тогда 


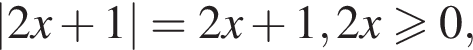



 Тогда
Тогда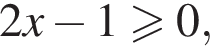





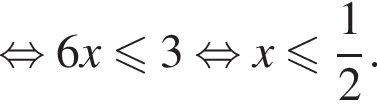




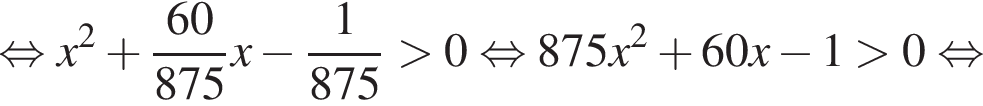


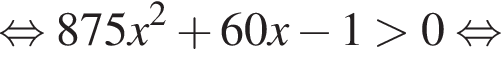
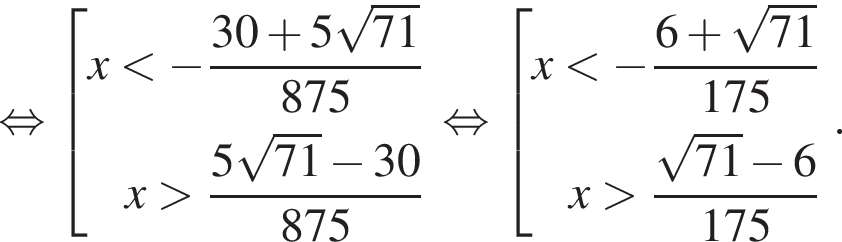


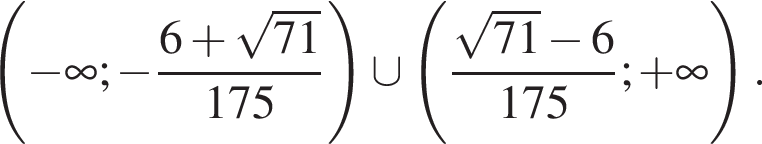
 и
и  и
и 




 (неравенство верно, так как
(неравенство верно, так как 
 ).
).
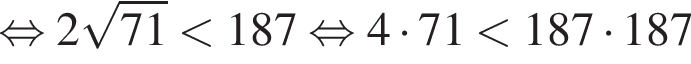










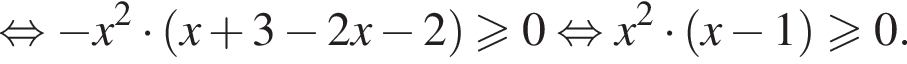

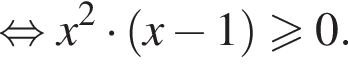

 Тогда
Тогда  и второе неравенство примет вид:
и второе неравенство примет вид: 





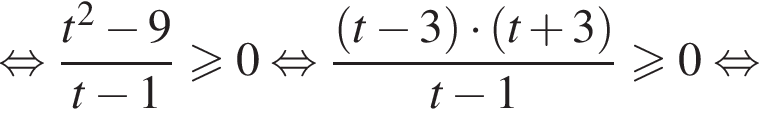





 Перейдем к переменной
Перейдем к переменной 


 Докажем это:
Докажем это: 


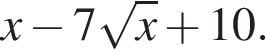 Ясно, что
Ясно, что  При
При  а само неравенство —
а само неравенство —  Тогда:
Тогда: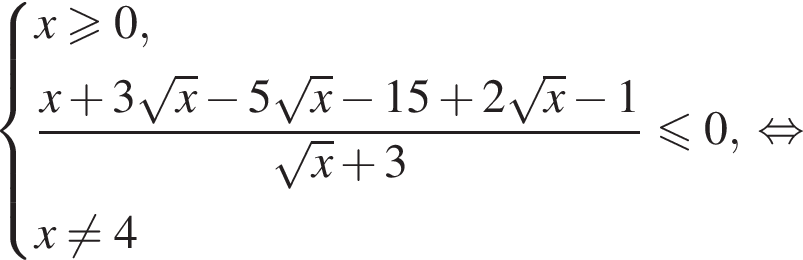




 т. е. при
т. е. при  или
или  было неположительным. Ясно, что это условие будет выполнено при
было неположительным. Ясно, что это условие будет выполнено при 



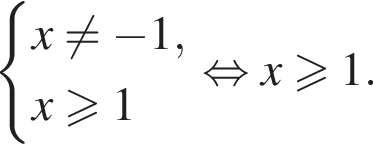
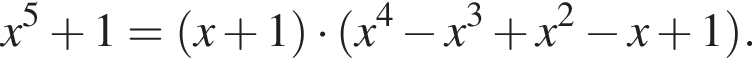 Поскольку число −1 не относится к числу решений неравенства, то мы вправе понизить степень числителя и знаменателя, разделив их на
Поскольку число −1 не относится к числу решений неравенства, то мы вправе понизить степень числителя и знаменателя, разделив их на 
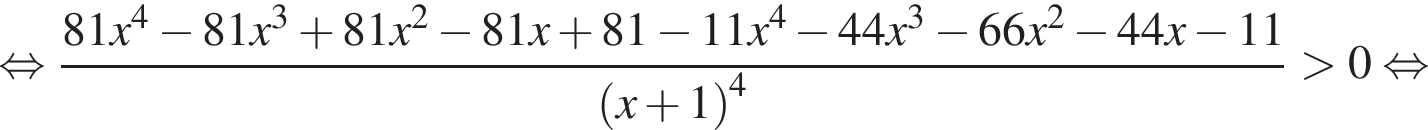


 Это симметрическое (возвратное) уравнение. Ясно, что
Это симметрическое (возвратное) уравнение. Ясно, что  Разделим обе части уравнения на
Разделим обе части уравнения на 
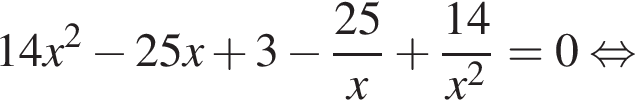



 тогда
тогда 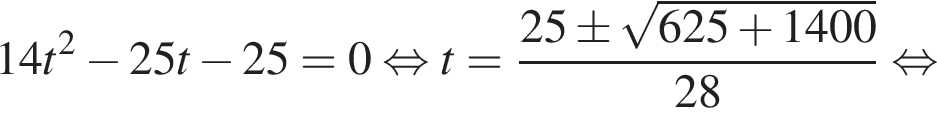



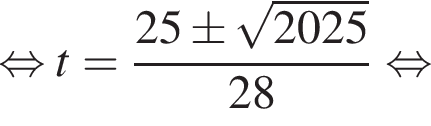



 Поскольку
Поскольку 





 решений не имеет, так как противоречит неравенству
решений не имеет, так как противоречит неравенству 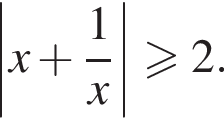


 Значит, интервал
Значит, интервал  и есть решения неравенства (*) на множестве
и есть решения неравенства (*) на множестве 
 Введем новую переменную. Пусть
Введем новую переменную. Пусть  Тогда
Тогда  Неравенство принимает вид:
Неравенство принимает вид:  Возведем обе части неравенства в третью степень и получим:
Возведем обе части неравенства в третью степень и получим: 






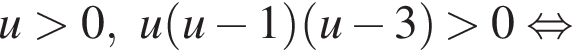













 где 1; 4; 6; 4; 1 — соответствующие биномиальные коэффициенты.
где 1; 4; 6; 4; 1 — соответствующие биномиальные коэффициенты.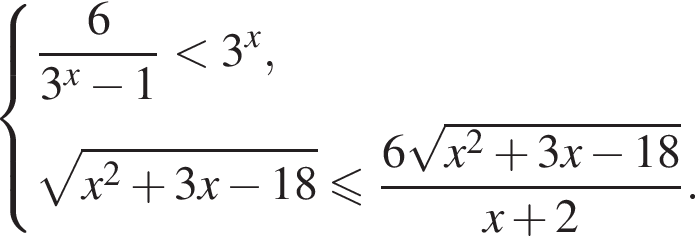







 Заметим, что левая часть неравенства положительна (равенство нулю мы уже рассмотрели выше). Следовательно, правая часть также обязана быть положительной. Но это условие выполнимо лишь при
Заметим, что левая часть неравенства положительна (равенство нулю мы уже рассмотрели выше). Следовательно, правая часть также обязана быть положительной. Но это условие выполнимо лишь при  Найдем значения x, при которых выполняется условие
Найдем значения x, при которых выполняется условие  Оно истинно при значениях переменной, удовлетворяющих совокупности неравенств:
Оно истинно при значениях переменной, удовлетворяющих совокупности неравенств:  и
и  разделить на
разделить на 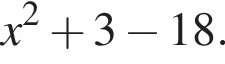 В результате получим:
В результате получим:  Решим это неравенство на
Решим это неравенство на 





















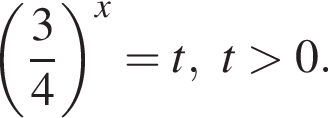 Тогда
Тогда 












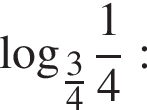


 Для таких
Для таких 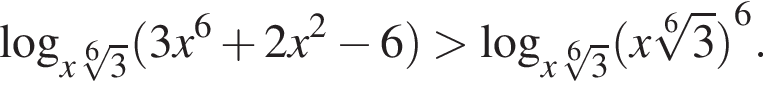






 и
и  Однако, для таких значений x осталось проверить выполнение условия
Однако, для таких значений x осталось проверить выполнение условия 
 на
на  является монотонно возрастающей как сумма двух возрастающих функций:
является монотонно возрастающей как сумма двух возрастающих функций: 
 и одной неубывающей функции
и одной неубывающей функции  Найдем знак функции в точках
Найдем знак функции в точках 
 Следовательно, множество
Следовательно, множество  Отсюда вывод: на промежутке
Отсюда вывод: на промежутке  функция
функция 

 Если нам удастся доказать, что
Если нам удастся доказать, что  то из истинности этого неравенства будет следовать также истинность неравенства
то из истинности этого неравенства будет следовать также истинность неравенства 


