
Найдите все значения a, при каждом из которых наибольшее значение функции  не меньше 1.
не меньше 1.
Решение. Снимем модуль, получим:
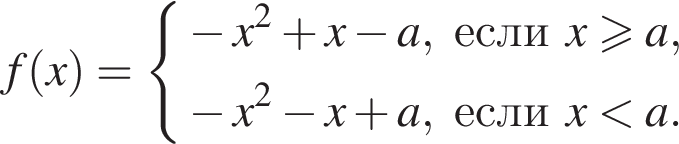
Функция f определена и непрерывна на всей вещественной оси, ее график состоит из частей двух парабол, ветви которых направлены вниз. Рассмотрим оба случая.
Если ![]() то
то  Этот квадратный трехчлен с отрицательным старшим коэффициентом принимает максимальное значение при
Этот квадратный трехчлен с отрицательным старшим коэффициентом принимает максимальное значение при 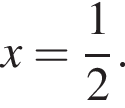 Находим:
Находим:

Найденное значение должно быть не меньше 1, откуда  При таких значениях параметра для
При таких значениях параметра для ![]() выполнено условие
выполнено условие ![]()
Если ![]() то
то  Этот квадратный трехчлен принимает наибольшее значение в точке
Этот квадратный трехчлен принимает наибольшее значение в точке  Находим:
Находим:
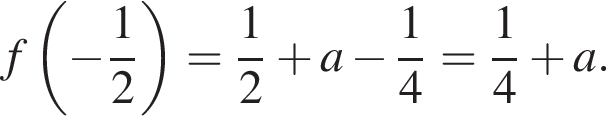
Найденное значение должно быть не меньше 1, откуда 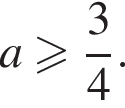 При таких значениях параметра для
При таких значениях параметра для  выполнено условие
выполнено условие ![]()
Ответ: 
Приведём другое решение.
Чтобы наибольшее значение данной функции было не меньше 1, необходимо и достаточно, чтобы она в какой-то точке приняла значение 1. В самом деле,  Если наибольшее значение ее не меньше единицы, то по непрерывности в какой-то точке будет значение единица. Если же наибольшее значение меньше единицы, то значение единица приниматься не может. Итак, задача свелась к такой — при каких a есть корни у уравнения
Если наибольшее значение ее не меньше единицы, то по непрерывности в какой-то точке будет значение единица. Если же наибольшее значение меньше единицы, то значение единица приниматься не может. Итак, задача свелась к такой — при каких a есть корни у уравнения  Поскольку
Поскольку  это уравнение равносильно совокупности
это уравнение равносильно совокупности

Эта совокупность имеет решения если  или если
или если  то есть при
то есть при 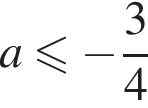 или
или 
Ответ: 
Приведем еще одно решение.
Заданная функция непрерывна и на бесконечностях стремится к минус бесконечности. Поэтому при любом значении параметра она достигает своего наибольшего значения. Тогда для того, чтобы наибольшее значение функции  было не меньше 1, необходимо и достаточно, чтобы неравенство
было не меньше 1, необходимо и достаточно, чтобы неравенство  имело решение. Запишем его в виде
имело решение. Запишем его в виде

и построим графики левой и правой частей неравенства.
График правой части неравенства — парабола, полученная из параболы, задаваемой уравнением ![]() сдвигом на 1 вверх вдоль оси ординат. График правой части неравенства получается сдвигом графика функции
сдвигом на 1 вверх вдоль оси ординат. График правой части неравенства получается сдвигом графика функции  сдвигом на |a| единиц вдоль оси абсцисс вправо или влево в зависимости от знака a.
сдвигом на |a| единиц вдоль оси абсцисс вправо или влево в зависимости от знака a.
Пусть при ![]() правая ветвь графика модуля касается параболы, а при
правая ветвь графика модуля касается параболы, а при ![]() — левая (см. рис.). Тогда при
— левая (см. рис.). Тогда при  парабола целиком лежит выше графика модуля и неравенство не имеет решений. При прочих значениях параметра неравенство имеет решения, поэтому осталось установить значения, соответствующие касанию.
парабола целиком лежит выше графика модуля и неравенство не имеет решений. При прочих значениях параметра неравенство имеет решения, поэтому осталось установить значения, соответствующие касанию.
При ![]() в силу равенства
в силу равенства  получаем уравнение
получаем уравнение  или
или  Случаю касания соответствует единственное решение этого уравнения, поэтому его дискриминант должен быть равен нулю:
Случаю касания соответствует единственное решение этого уравнения, поэтому его дискриминант должен быть равен нулю:  откуда
откуда  Аналогично для
Аналогично для ![]() получаем уравнение
получаем уравнение 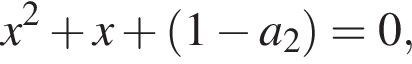 откуда находим
откуда находим  или
или  Тем самым,
Тем самым, 
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен правильный ответ. | 4 |
| С помощью верного рассуждения получены оба верных значения параметра, но – или в ответ включены также и одно-два неверных значения; – или решение недостаточно обосновано. | 3 |
| С помощью верного рассуждения получено хотя бы одно верное значение параметра. | 2 |
| Задача сведена к исследованию: – или взаимного расположения трёх окружностей; – или двух квадратных уравнений с параметром. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |




 то есть на отрезке
то есть на отрезке 





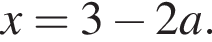 Возможное расположение этих парабол показано на рисунках.
Возможное расположение этих парабол показано на рисунках. — то в точке
— то в точке  либо
либо 






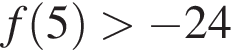 и
и  Имеем:
Имеем:
 верно для всех х.
верно для всех х.  и запишем неравенство в виде
и запишем неравенство в виде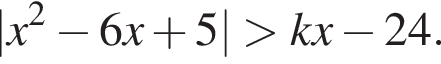
 а на этом отрезке является отражением лежащей ниже оси абсцисс части этой параболы в верхнюю полуплоскость (см. рис.).
а на этом отрезке является отражением лежащей ниже оси абсцисс части этой параболы в верхнюю полуплоскость (см. рис.). и параболы
и параболы  Для этого приравняем к нулю дискриминант квадратного уравнения
Для этого приравняем к нулю дискриминант квадратного уравнения 




 касание происходит именно с графиком функции
касание происходит именно с графиком функции  а не с лежащей ниже оси абсцисс частью параболы
а не с лежащей ниже оси абсцисс частью параболы  Рассмотрим прямую p, проходящую через точки с координатами (0; −24) и (5; 0). Определим ее угловой коэффициент:
Рассмотрим прямую p, проходящую через точки с координатами (0; −24) и (5; 0). Определим ее угловой коэффициент:  Сравним угловые коэффициенты k1 и k2:
Сравним угловые коэффициенты k1 и k2:

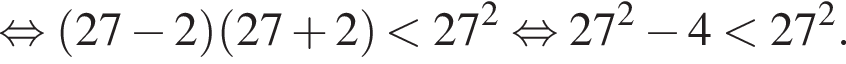
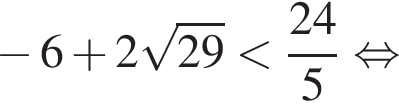

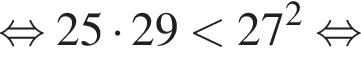




 а потому справа от общей точки (0; −24) касательная проходит ниже прямой p и, значит, касается параболы в точке лежащей выше оси абсцисс. Тем самым подходят все значения k такие, что:
а потому справа от общей точки (0; −24) касательная проходит ниже прямой p и, значит, касается параболы в точке лежащей выше оси абсцисс. Тем самым подходят все значения k такие, что:  Возвращаясь к параметру a, получаем:
Возвращаясь к параметру a, получаем: 

 не менее 6.
не менее 6. является парабола, ветви которой направлены вверх, а вершина имеет координаты
является парабола, ветви которой направлены вверх, а вершина имеет координаты  Значит, минимум функции
Значит, минимум функции 
 если эта точка принадлежит множеству, либо в одной из граничных точек
если эта точка принадлежит множеству, либо в одной из граничных точек 










 имеем:
имеем:  значит, наименьшее значение функции достигается в точке
значит, наименьшее значение функции достигается в точке  и
и  что удовлетворяет условию задачи.
что удовлетворяет условию задачи. значит, наименьшее значение функции достигается в одной из граничных точек
значит, наименьшее значение функции достигается в одной из граничных точек  в которых значение функции не меньше 6.
в которых значение функции не меньше 6. значит, наименьшее значение функции достигается в точке
значит, наименьшее значение функции достигается в точке  что не удовлетворяет условию задачи.
что не удовлетворяет условию задачи.

 поэтому ее график есть часть параболы с ветвями, направленными вверх, и осью симметрии
поэтому ее график есть часть параболы с ветвями, направленными вверх, и осью симметрии  поэтому ее график есть часть параболы с ветвями, направленными вверх, и осью симметрии
поэтому ее график есть часть параболы с ветвями, направленными вверх, и осью симметрии 
 имеет более двух точек экстремума, а именно три, в единственном случае (рис. 1):
имеет более двух точек экстремума, а именно три, в единственном случае (рис. 1): 





 тогда
тогда  при этом, если x — целое, то y — также целое число.
при этом, если x — целое, то y — также целое число. Построим график функции
Построим график функции  при
при  то целые числа −4 и −3 также будут решениями, и тогда будет, по крайней мере, три решения данного неравенства:
то целые числа −4 и −3 также будут решениями, и тогда будет, по крайней мере, три решения данного неравенства:  Следовательно,
Следовательно, 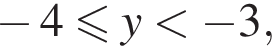 и, стало быть,
и, стало быть,  Значит, должно выполняться двойное неравенство:
Значит, должно выполняться двойное неравенство:  откуда
откуда 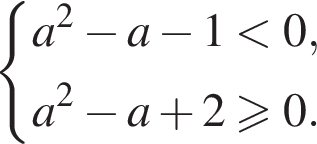
 Второе неравенство выполняется при всех
Второе неравенство выполняется при всех 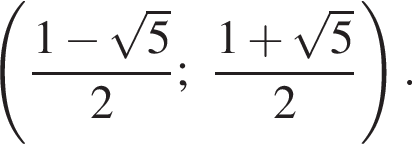
 есть ровно одно целое число.
есть ровно одно целое число. при любом a имеет решение
при любом a имеет решение  Значит, при любом a одно из значений функции равно 1.
Значит, при любом a одно из значений функции равно 1.




 содержит отрезок
содержит отрезок  и заметим, что для любого значения параметра а знаменатель положителен при всех значениях переменной x. Следовательно, заданная функция непрерывна, и тогда отрезок [0; 1] лежит во множестве ее значений тогда и только тогда, когда уравнения
и заметим, что для любого значения параметра а знаменатель положителен при всех значениях переменной x. Следовательно, заданная функция непрерывна, и тогда отрезок [0; 1] лежит во множестве ее значений тогда и только тогда, когда уравнения  и
и  имеют решения.
имеют решения. оно имеет решение при любом
оно имеет решение при любом  Оно имеет решение тогда и только тогда, когда его дискриминант неотрицателен:
Оно имеет решение тогда и только тогда, когда его дискриминант неотрицателен:





 или
или 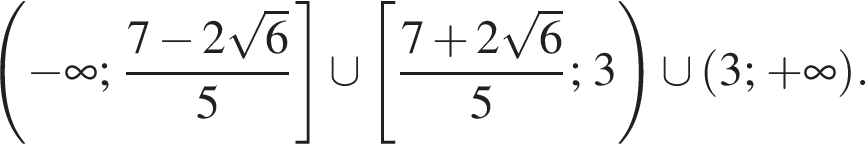


 имеет менее трех различных корней.
имеет менее трех различных корней. и
и 
 то
то  и
и 
 или
или  то есть при
то есть при 
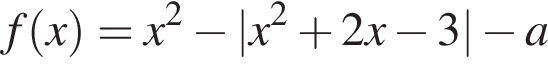
 График функции
График функции  или
или  и
и 
 то
то 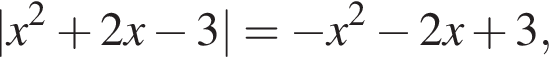 и
и 
 Соответствующие значения функции g равны:
Соответствующие значения функции g равны:

 меньше 2.
меньше 2. разбивают действительную ось на промежутки, в каждом из которых графиком данной функции является часть некоторой параболы. Заметим, что при
разбивают действительную ось на промежутки, в каждом из которых графиком данной функции является часть некоторой параболы. Заметим, что при  значения данной функции неограниченно возрастают. Следовательно, свое наименьшее значение данная функция принимает в одной из точек (или в нескольких этих точках)
значения данной функции неограниченно возрастают. Следовательно, свое наименьшее значение данная функция принимает в одной из точек (или в нескольких этих точках) 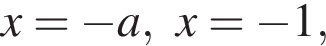
 где
где  и
и  или
или  и
и  Абсциссы их вершин соответственно
Абсциссы их вершин соответственно 
 меньше 2 тогда и только тогда, когда выполняется хотя бы одно из неравенств:
меньше 2 тогда и только тогда, когда выполняется хотя бы одно из неравенств: 




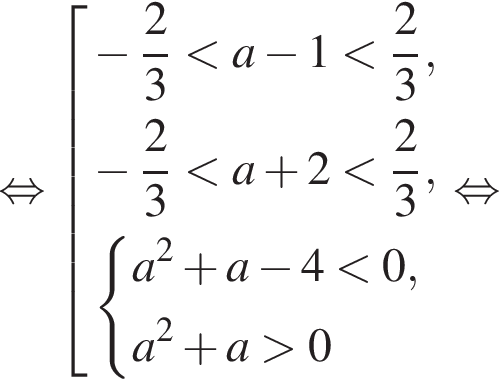
 получаем
получаем 
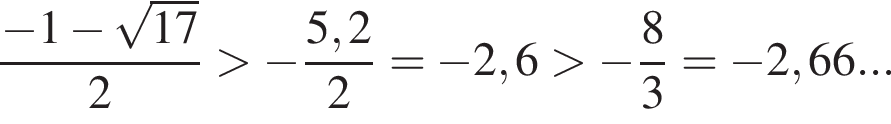


 но дальнейшие рассуждения неверны или отсутствуют.
но дальнейшие рассуждения неверны или отсутствуют. и
и 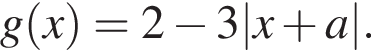
 больше −2.
больше −2. стоящее под знаком модуля выражение отрицательно, а задающее функцию выражение является квадратным трехчленом с положительным старшим коэффициентом:
стоящее под знаком модуля выражение отрицательно, а задающее функцию выражение является квадратным трехчленом с положительным старшим коэффициентом:




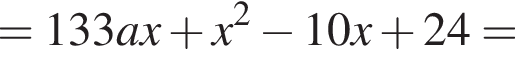
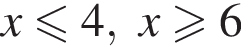 стоящее под знаком модуля выражение положительно, а задающее функцию выражение является квадратным трехчленом с отрицательным старшим коэффициентом:
стоящее под знаком модуля выражение положительно, а задающее функцию выражение является квадратным трехчленом с отрицательным старшим коэффициентом:






 то наибольшее значение функции будет достигаться или в точке 4, или в точке 6. В остальных случаях наибольшее значение функции будет достигаться в точке
то наибольшее значение функции будет достигаться или в точке 4, или в точке 6. В остальных случаях наибольшее значение функции будет достигаться в точке  Значит, наибольшее значение функции будет больше −2 при выполнении следующих условий (⁎):
Значит, наибольшее значение функции будет больше −2 при выполнении следующих условий (⁎):



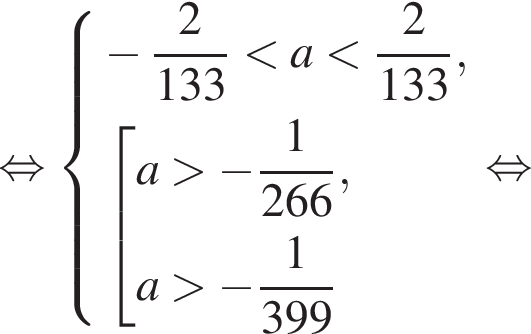



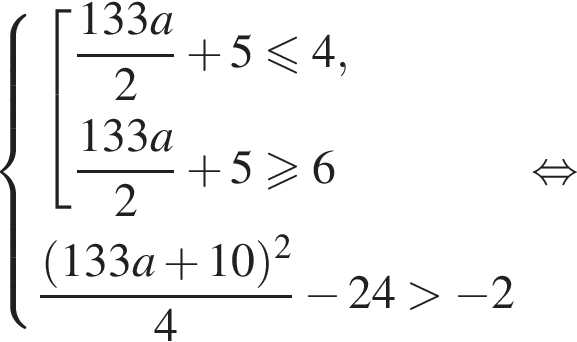
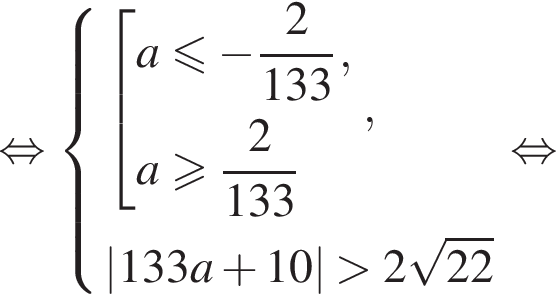
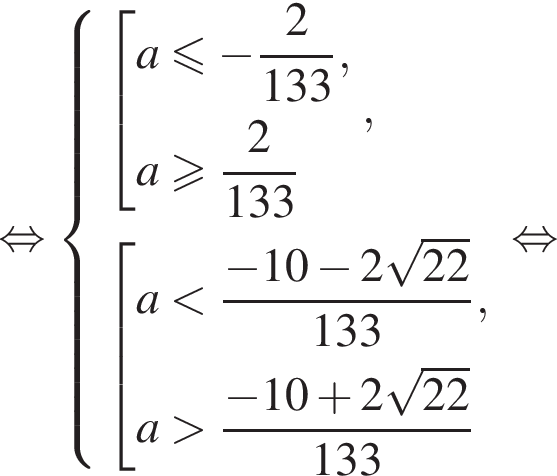

 или
или 
 имеет ровно два экстремума на промежутке (−2; 3).
имеет ровно два экстремума на промежутке (−2; 3). тогда
тогда


 тогда
тогда  Найдем нули производной:
Найдем нули производной: 







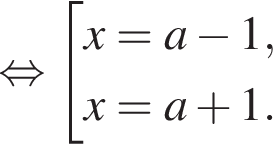



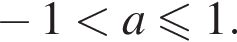

 содержит промежуток
содержит промежуток  При каждом таком а укажите множество значений функции
При каждом таком а укажите множество значений функции  тогда и только тогда, когда уравнения
тогда и только тогда, когда уравнения  и
и  будут иметь решения. Рассмотрим эти уравнения:
будут иметь решения. Рассмотрим эти уравнения: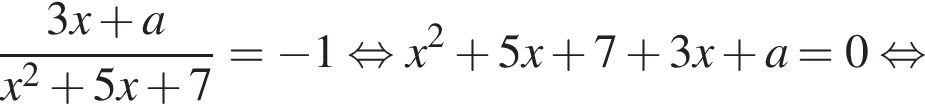







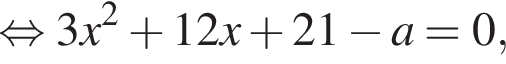




 Для этого рассмотрим данное равенство как уравнение с переменной х и параметром
Для этого рассмотрим данное равенство как уравнение с переменной х и параметром 
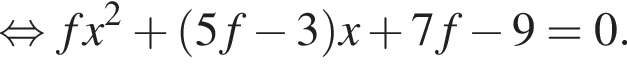

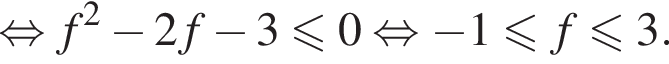




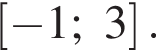
 пересекает ось ординат в точке А и имеет ровно две общие точки M и N с осью абсцисс. Прямая, касающаяся этого графика в точке M, проходит через точку А. Найдите а, b и с, если площадь треугольника AMN равна 1.
пересекает ось ординат в точке А и имеет ровно две общие точки M и N с осью абсцисс. Прямая, касающаяся этого графика в точке M, проходит через точку А. Найдите а, b и с, если площадь треугольника AMN равна 1.


 Но тогда:
Но тогда: 
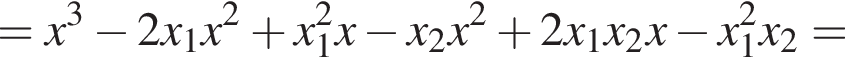


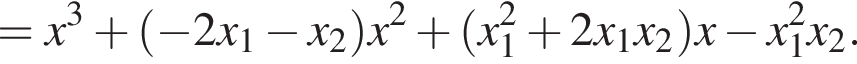
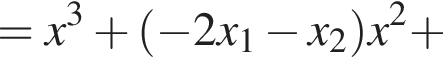


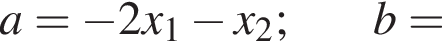

 в точке (x2; 0). Это уравнение имеет вид:
в точке (x2; 0). Это уравнение имеет вид:  или
или 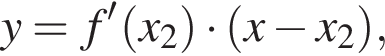 где
где 



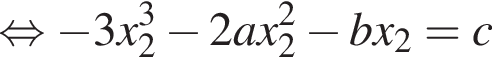



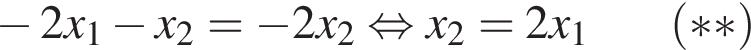
 и
и 
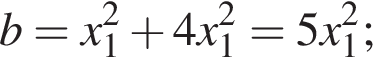





 Но тогда
Но тогда








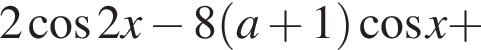



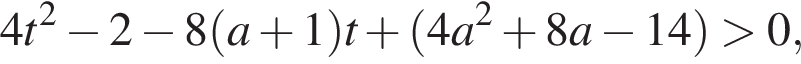




 то неравенство не выполняется, например, при
то неравенство не выполняется, например, при  при всех t из отрезка
при всех t из отрезка  поэтому нужно, чтобы
поэтому нужно, чтобы 
 то
то  при всех t из отрезка
при всех t из отрезка  поэтому нужно, чтобы
поэтому нужно, чтобы 
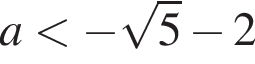 или
или  на отрезке [−1; 3] не меньшее, чем −5.
на отрезке [−1; 3] не меньшее, чем −5. должно выполняться на всем промежутке
должно выполняться на всем промежутке  То есть
То есть










 (верно при
(верно при  ),
), (верно при
(верно при  ),
), (верно при
(верно при 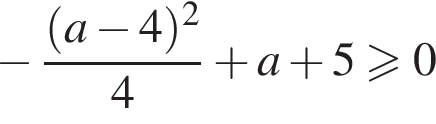 при
при 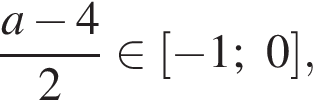 то есть при
то есть при  (нас не интересует, поскольку уже установлено, что
(нас не интересует, поскольку уже установлено, что 
 при
при  то есть при
то есть при  (то есть это обязательно надо проверить, при
(то есть это обязательно надо проверить, при 

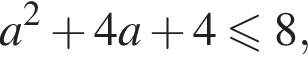






 Это означает, что, например, множество значений функции на отрезках
Это означает, что, например, множество значений функции на отрезках  Выделим целую часть:
Выделим целую часть:
 имеем
имеем  то есть график функции имеет горизонтальную асимптоту y = – 12. Но в то же время
то есть график функции имеет горизонтальную асимптоту y = – 12. Но в то же время  что невозможно для убывающей функции.
что невозможно для убывающей функции. при каждом из которых наименьшее значение функции
при каждом из которых наименьшее значение функции 
 принимает наименьшее значение.
принимает наименьшее значение.




 корни производной суть числа 0 и −1. Отрезок
корни производной суть числа 0 и −1. Отрезок  то
то  а
а  не лежит на отрезке
не лежит на отрезке  В этом случае имеем следующее расположение знаков производной:
В этом случае имеем следующее расположение знаков производной:

 )
) то производная имеет вид
то производная имеет вид  Отрезок
Отрезок  на нем функция лежит единственный корень производной — число 0. Это точка максимума, поэтому наименьшее значение достигается или на левой границе отрезка, или на правой границе. Эти значения равны, будем считать, что наименьшее значение достигается на левой границе (***).
на нем функция лежит единственный корень производной — число 0. Это точка максимума, поэтому наименьшее значение достигается или на левой границе отрезка, или на правой границе. Эти значения равны, будем считать, что наименьшее значение достигается на левой границе (***). то ее наименьшее значение равно наименьшему из значений
то ее наименьшее значение равно наименьшему из значений  и
и  Имеем:
Имеем:














 то
то  а
а  то функция убывает на
то функция убывает на  и на
и на  Проведя аналогичные вычисления, можно получить, что ее наименьшее значение равно
Проведя аналогичные вычисления, можно получить, что ее наименьшее значение равно



 функции переходят друг в друга, достаточно будет исследовать одну из них. Иными словами, поскольку для всех α из отрезка
функции переходят друг в друга, достаточно будет исследовать одну из них. Иными словами, поскольку для всех α из отрезка  достаточно найти наименьшее значение функции
достаточно найти наименьшее значение функции  на промежутке
на промежутке 


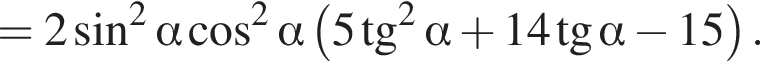


 являются числа
являются числа  и
и  На интервале
На интервале 
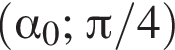 положительна. Следовательно, функция
положительна. Следовательно, функция  Поэтому наименьшее значение
Поэтому наименьшее значение  достигается в точке
достигается в точке  принадлежащей отрезку
принадлежащей отрезку 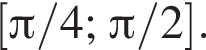
 и
и 
 имеет ровно два неотрицательных решения.
имеет ровно два неотрицательных решения.
 и
и  разбивают плоскость на 4 области. Выражение
разбивают плоскость на 4 области. Выражение 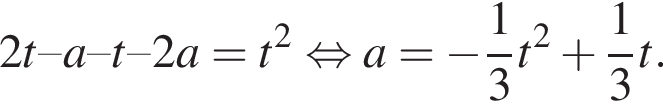 График функции — парабола с вершиной в точке
График функции — парабола с вершиной в точке  ветви которой направлены вниз.
ветви которой направлены вниз. 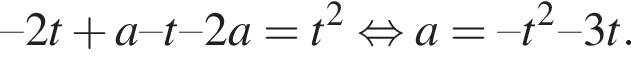 График функции — парабола с вершиной в точке
График функции — парабола с вершиной в точке 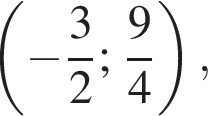 ветви которой направлены вниз.
ветви которой направлены вниз.  График функции — парабола с вершиной в точке
График функции — парабола с вершиной в точке  ветви которой направлены вверх.
ветви которой направлены вверх. График функции — парабола с вершиной в точке
График функции — парабола с вершиной в точке 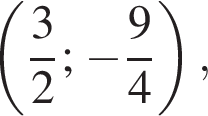 ветви которой направлены вверх.
ветви которой направлены вверх. 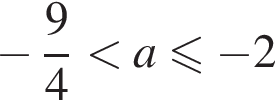 (выделено красным).
(выделено красным).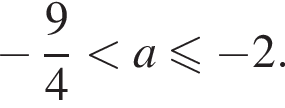
 строить график уравнения имеет смысл только в первой и четвертой координатных четвертях и исключенной точкой О(0; 0). Это наблюдение позволяет заметно сократить решение.
строить график уравнения имеет смысл только в первой и четвертой координатных четвертях и исключенной точкой О(0; 0). Это наблюдение позволяет заметно сократить решение.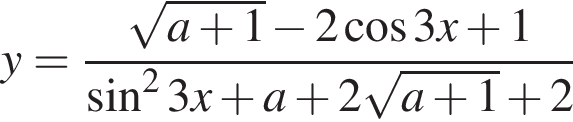 содержит отрезок
содержит отрезок  тогда
тогда  причем
причем 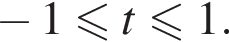 Пусть, далее,
Пусть, далее,  тогда
тогда 
 и заметим, что в силу неотрицательности b справедливо неравенство
и заметим, что в силу неотрицательности b справедливо неравенство  при
при  содержит отрезок [2; 3].
содержит отрезок [2; 3].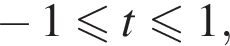 а значит, знаменатель дроби не меньше 1. Следовательно, функция
а значит, знаменатель дроби не меньше 1. Следовательно, функция  и
и  имеют решения, удовлетворяющие условию
имеют решения, удовлетворяющие условию 



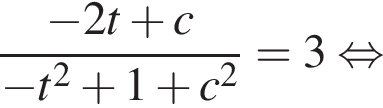


 Тем самым, свободные члены квадратных трехчленов
Тем самым, свободные члены квадратных трехчленов  и
и  отрицательны, а значит, их графики пересекают ось ординат в точках с отрицательной абсциссой. Ветви соответствующих парабол направлены вверх, их вершины лежат ниже оси абсцисс на прямых
отрицательны, а значит, их графики пересекают ось ординат в точках с отрицательной абсциссой. Ветви соответствующих парабол направлены вверх, их вершины лежат ниже оси абсцисс на прямых  оси абсцисс хотя бы в одной точке тогда и только тогда, когда
оси абсцисс хотя бы в одной точке тогда и только тогда, когда  и
и  одновременно. Имеем:
одновременно. Имеем:






 имеет 4 решения, где f — четная периодическая функция с периодом
имеет 4 решения, где f — четная периодическая функция с периодом  определенная на всей числовой прямой, причем
определенная на всей числовой прямой, причем  если
если 
 единственную общую точку.
единственную общую точку. (изображен красным) проходит через точку A
(изображен красным) проходит через точку A Составим уравнение:
Составим уравнение:

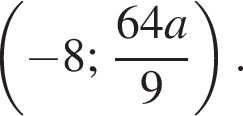 Составим уравнение:
Составим уравнение:

 или
или 



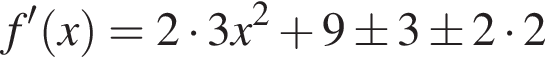 положительна при любом случае раскрытия модулей. Следовательно, функция f возрастает. Тогда и вся левая часть заданного неравенства возрастает функцией как сумма возрастающих функций. Поэтому неравенство будет выполняться для всех значений x из отрезка [−2; 1] тогда и только тогда, когда оно выполнено в точке x = 1. Имеем:
положительна при любом случае раскрытия модулей. Следовательно, функция f возрастает. Тогда и вся левая часть заданного неравенства возрастает функцией как сумма возрастающих функций. Поэтому неравенство будет выполняться для всех значений x из отрезка [−2; 1] тогда и только тогда, когда оно выполнено в точке x = 1. Имеем:



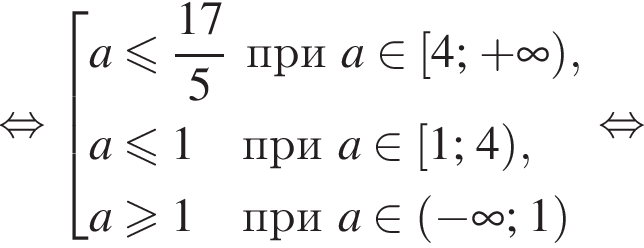
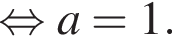
 можно решить графически. Обозначим левую часть неравенства
можно решить графически. Обозначим левую часть неравенства  и отметим, что эта функция принимает наименьшее значение в точке
и отметим, что эта функция принимает наименьшее значение в точке  Во всех остальных точках
Во всех остальных точках  Следовательно,
Следовательно, 

 Имеем:
Имеем:





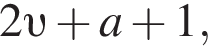 модули раскроются по-разному. При этом на каждом участке непрерывная функция f(x) будет линейной с угловым коэффициентом
модули раскроются по-разному. При этом на каждом участке непрерывная функция f(x) будет линейной с угловым коэффициентом  Какова бы ни была комбинация знаков,
Какова бы ни была комбинация знаков,  выполняется при всех
выполняется при всех  если и только если
если и только если 


 — возрастающая линейная с угловым коэффициентом
— возрастающая линейная с угловым коэффициентом  При больших
При больших  (см. рис.). Поэтому функция
(см. рис.). Поэтому функция  выполняется при всех
выполняется при всех  и
и  Получаем:
Получаем:


 модуль раскрывается «со знаком минус»:
модуль раскрывается «со знаком минус»:  На отрезке [1; 3] график функции представляет собой параболу, ветви которой направлены вниз.
На отрезке [1; 3] график функции представляет собой параболу, ветви которой направлены вниз.  График функции на этих лучах представляет собой параболу, ветви которой направлены вверх. Вершина этой параболы может лежать левее отрезка [1; 3], правее этого отрезка или на самом отрезке. Рассмотрим эти случаи.
График функции на этих лучах представляет собой параболу, ветви которой направлены вверх. Вершина этой параболы может лежать левее отрезка [1; 3], правее этого отрезка или на самом отрезке. Рассмотрим эти случаи. то есть если
то есть если 







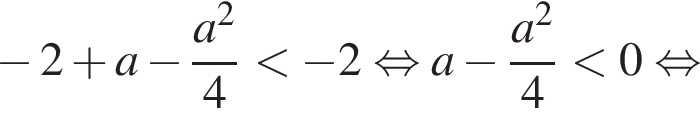






 получаем:
получаем: 
 а наименьшее значение функции достигается на концах отрезка. Найдем
а наименьшее значение функции достигается на концах отрезка. Найдем  и
и  Наименьшее значение функции может быть меньше −2, только если
Наименьшее значение функции может быть меньше −2, только если  то есть при
то есть при 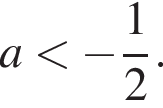 Учитывая ограничения на a, получаем:
Учитывая ограничения на a, получаем: 

 имело решение. Запишем его в виде
имело решение. Запишем его в виде
 должен быть больше углового коэффициента прямой, проходящей через точку (3; 0). Имеем:
должен быть больше углового коэффициента прямой, проходящей через точку (3; 0). Имеем: 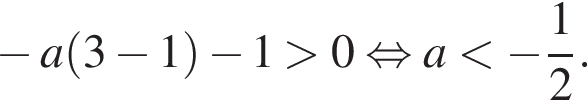
 в виде
в виде  и найдем дискриминант полученного квадратного уравнения:
и найдем дискриминант полученного квадратного уравнения: 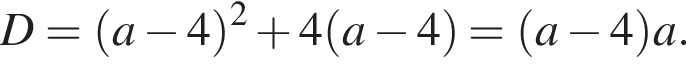 Парабола имеет с касательной единственную общую точку, поэтому касанию соответствует дискриминант, равный нулю, откуда a = 0 или a = 4. Подходит только положительный корень, соответствующий отрицательному угловому коэффициенту прямой.
Парабола имеет с касательной единственную общую точку, поэтому касанию соответствует дискриминант, равный нулю, откуда a = 0 или a = 4. Подходит только положительный корень, соответствующий отрицательному угловому коэффициенту прямой.
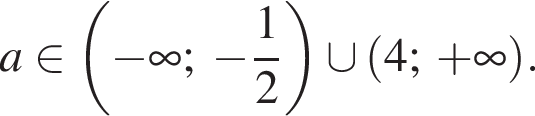
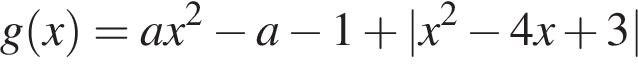 аналогичная переформулировка не будет равносильна изначальной задаче.
аналогичная переформулировка не будет равносильна изначальной задаче. 

 перепишем уравнение в виде:
перепишем уравнение в виде: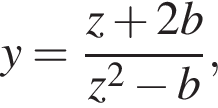
 а
а  Дальнейшие рассуждения свяжем с соотношением
Дальнейшие рассуждения свяжем с соотношением

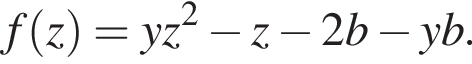
 существует корень квадратного трёхчлена
существует корень квадратного трёхчлена  где
где  приходим к рассмотрению неравенства
приходим к рассмотрению неравенства

 то так как
то так как  для
для 
 будет выполняться при всех
будет выполняться при всех  Следующий шаг в решении задачи состоит в том, чтобы среди найденных значений параметра b, при которых существуют корни уравнения
Следующий шаг в решении задачи состоит в том, чтобы среди найденных значений параметра b, при которых существуют корни уравнения  и
и  то
то  и поэтому хотя бы один корень квадратного трёхчлена
и поэтому хотя бы один корень квадратного трёхчлена 

 графиком которой является гипербола, принимает наименьшее своё значение на отрезке [1; 2], равное
графиком которой является гипербола, принимает наименьшее своё значение на отрезке [1; 2], равное 
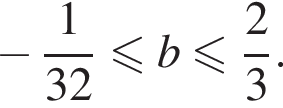

 либо
либо 
 При
При 
 При
При 
 Но у нас
Но у нас  и, таким образом, значение
и, таким образом, значение 





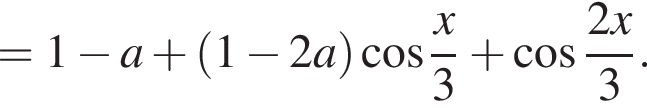
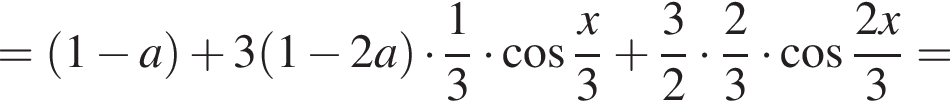






 то
то  Значит, уравнение
Значит, уравнение  даёт две критические точки на заданном интервале. Рассмотрим четыре возможных случая.
даёт две критические точки на заданном интервале. Рассмотрим четыре возможных случая. или
или  то уравнение
то уравнение  не имеет корней на заданном интервале. Тогда функция
не имеет корней на заданном интервале. Тогда функция  или
или 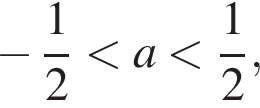 то уравнение
то уравнение  Тогда функция
Тогда функция  то корни уравнения
то корни уравнения  то уравнение
то уравнение  при
при 

 на отрезке [−1; 0] не превышает единицы и достигается на левом конце отрезка.
на отрезке [−1; 0] не превышает единицы и достигается на левом конце отрезка.






 на отрезке
на отрезке  возрастает, значит, наименьшее значение функции на этом отрезке достигается в точке
возрастает, значит, наименьшее значение функции на этом отрезке достигается в точке  — на левом конце отрезка, и равно
— на левом конце отрезка, и равно 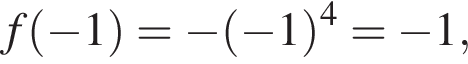 что удовлетворяет условию задачи.
что удовлетворяет условию задачи.
 Тогда
Тогда  при
при  при
при  а
а  Условие задачи будет выполнено если
Условие задачи будет выполнено если  то есть при
то есть при  Найдём соответствующие значения параметра a:
Найдём соответствующие значения параметра a:




 Тогда
Тогда  а
а  Условие задачи будет выполнено если
Условие задачи будет выполнено если  то есть при
то есть при  Найдём соответствующие значения параметра a:
Найдём соответствующие значения параметра a:



 не больше расстояния между точками экстремума функции
не больше расстояния между точками экстремума функции 
 найдем модуль их разности:
найдем модуль их разности:

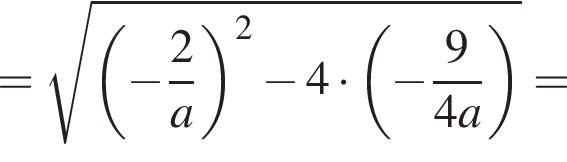



 найдём при помощи производной:
найдём при помощи производной:
 являются точками экстремума функции
являются точками экстремума функции 
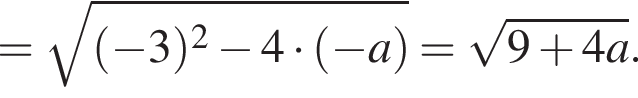












 и
и  и
и 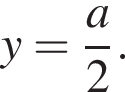
 и
и  и
и  поэтому должно выполняться неравенство
поэтому должно выполняться неравенство  откуда a < 4. Одна из сторон этого треугольника параллельна оси абсцисс. Чтобы найти ее длину, определим абсциссы точек пересечения линий:
откуда a < 4. Одна из сторон этого треугольника параллельна оси абсцисс. Чтобы найти ее длину, определим абсциссы точек пересечения линий: 

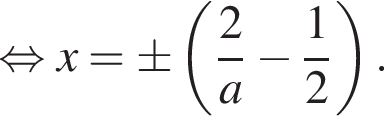






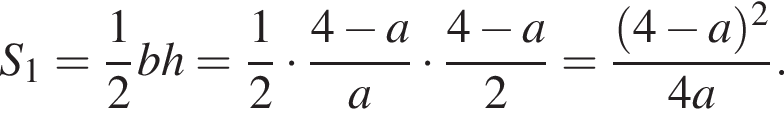
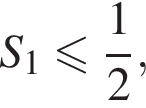 откуда находим:
откуда находим:


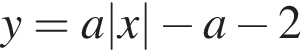 и
и  откуда
откуда  (см. рис. 2). Абсциссы точек пересечения линий найдем из уравнения
(см. рис. 2). Абсциссы точек пересечения линий найдем из уравнения  получим:
получим: 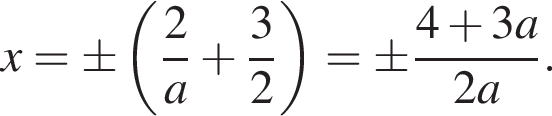
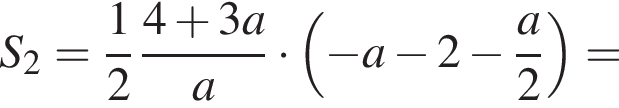



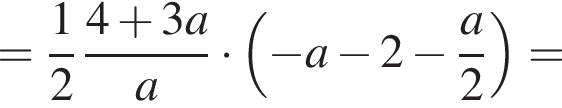
 записывается в виде
записывается в виде



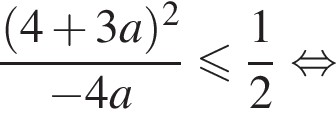


 или
или  на отрезке [−1; 1] имеет только одну точку минимума.
на отрезке [−1; 1] имеет только одну точку минимума.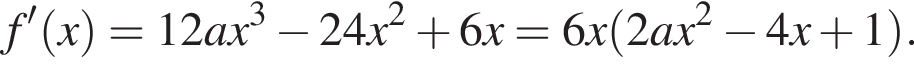


 принимает вид
принимает вид  и имеет единственный корень
и имеет единственный корень  лежащий на заданном отрезке. При этом в точке x = 0 производная меняет знак с минуса на плюс, а потому это точка минимума, в точке
лежащий на заданном отрезке. При этом в точке x = 0 производная меняет знак с минуса на плюс, а потому это точка минимума, в точке  то есть при
то есть при  Тогда уравнение
Тогда уравнение 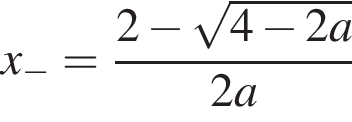 и
и  причем
причем 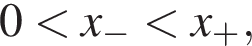 и потому 0 и
и потому 0 и  откуда
откуда  то есть
то есть  Полученное неравенство обращается в равенство при
Полученное неравенство обращается в равенство при  причем левая часть неравенства убывает на ОДЗ, а правая — возрастает. Следовательно, решениями неравенства являются значения параметра, для которых
причем левая часть неравенства убывает на ОДЗ, а правая — возрастает. Следовательно, решениями неравенства являются значения параметра, для которых  Учитывая, что
Учитывая, что  заключаем, что подходят все а такие, что
заключаем, что подходят все а такие, что 
 или
или 




 Точка 0 является точкой минимума, точка
Точка 0 является точкой минимума, точка 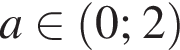 уравнение уравнение
уравнение уравнение 
 и
и 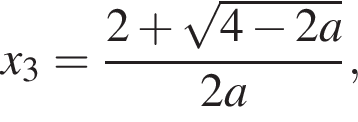
 что невозможно для положительных а, либо
что невозможно для положительных а, либо  откуда
откуда  Левая часть неравенства убывает на интервале
Левая часть неравенства убывает на интервале  или при
или при 






 решением системы является интервал
решением системы является интервал  решением системы является интервал
решением системы является интервал 


 функция принимает вид
функция принимает вид  а при
а при  функция принимает вид
функция принимает вид 
 является чётной функцией. Рассмотрим её на промежутке
является чётной функцией. Рассмотрим её на промежутке  На этом промежутке
На этом промежутке  Тогда её производная
Тогда её производная  Стационарная точка
Стационарная точка  При этом
При этом 












 и
и 
 уравнение
уравнение  имеет ровно четыре решения.
имеет ровно четыре решения. Для того, чтобы уравнение
Для того, чтобы уравнение  был больше наименьшего значения квадратичной функции
был больше наименьшего значения квадратичной функции 





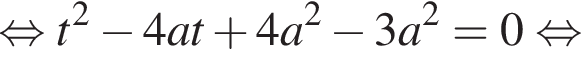








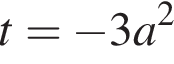 достигается при
достигается при  а потому является наименьшим значением функции
а потому является наименьшим значением функции 

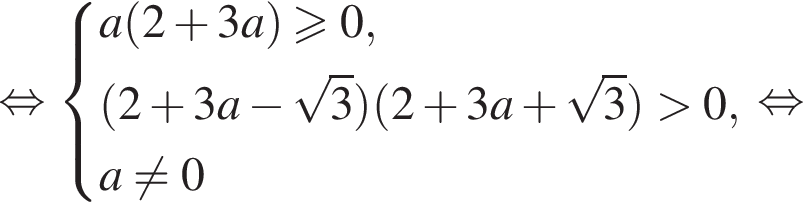


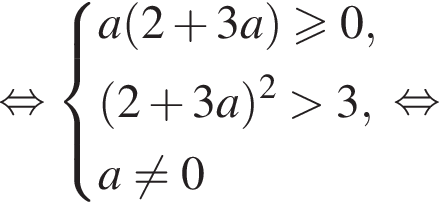





 имеет хотя бы один корень, если
имеет хотя бы один корень, если 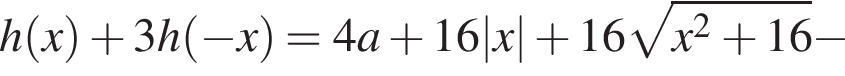


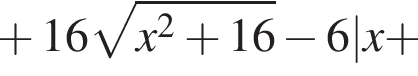

 в равенство из условия, получаем:
в равенство из условия, получаем:
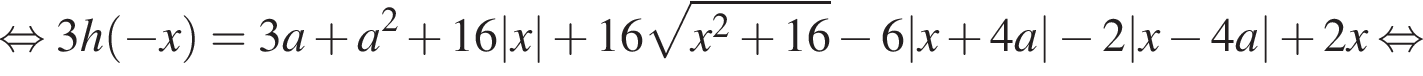



 при всех x. Положим
при всех x. Положим 


 Для отрицательных x функция f возрастает, так как при любом раскрытии модулей коэффициент при x положительный. Для неотрицательных x функция f убывает, поскольку при любом раскрытии модулей коэффициент при x отрицательный. Значит,
Для отрицательных x функция f возрастает, так как при любом раскрытии модулей коэффициент при x положительный. Для неотрицательных x функция f убывает, поскольку при любом раскрытии модулей коэффициент при x отрицательный. Значит, 

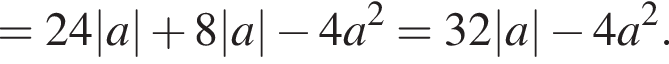


 может иметь корни, только если
может иметь корни, только если 








 и
и  и ветвями, направленными вверх и вниз. Прямая, перпендикулярная оси ординат, может иметь одну, две или три общие точки с графиком такой функции. Если найдётся прямая
и ветвями, направленными вверх и вниз. Прямая, перпендикулярная оси ординат, может иметь одну, две или три общие точки с графиком такой функции. Если найдётся прямая  которая имеет три общие точки, то хотя бы одна из прямых
которая имеет три общие точки, то хотя бы одна из прямых  или
или  будет иметь ровно две общие точки.
будет иметь ровно две общие точки.  Следовательно, искомые значения параметра задаются системой неравенств:
Следовательно, искомые значения параметра задаются системой неравенств:

 меньше 1.
меньше 1. получаем, что
получаем, что  График этой функции на рассматриваемом промежутке состоит из двух частей параболы, ветви которой направлены вверх, и осью симметрии
График этой функции на рассматриваемом промежутке состоит из двух частей параболы, ветви которой направлены вверх, и осью симметрии  При
При  находим
находим  а график этой функции на рассматриваемом промежутке — часть параболы с ветвями, направленными вниз.
а график этой функции на рассматриваемом промежутке — часть параболы с ветвями, направленными вниз.

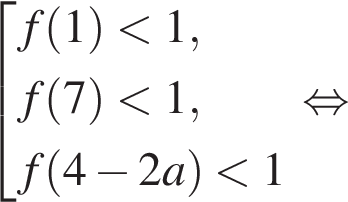
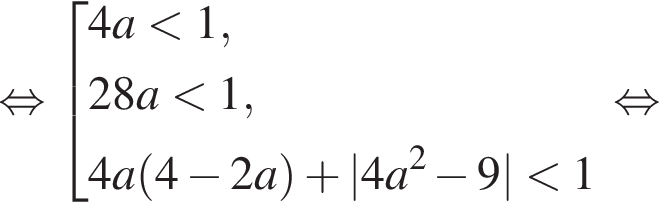
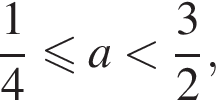 то второе неравенство принимает вид
то второе неравенство принимает вид  откуда
откуда  или
или Эти промежутки не содержат полуинтервал
Эти промежутки не содержат полуинтервал 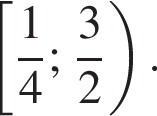 Если
Если  то
то  откуда
откуда  или
или Значит,
Значит,  Таким образом,
Таким образом, 
 и
и  больше 6, но не больше 12.
больше 6, но не больше 12.


 График
График  а график
а график  — в точке
— в точке 

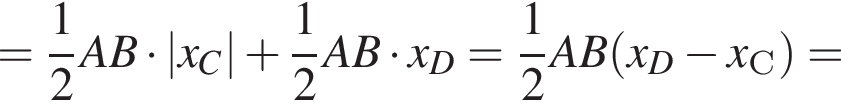


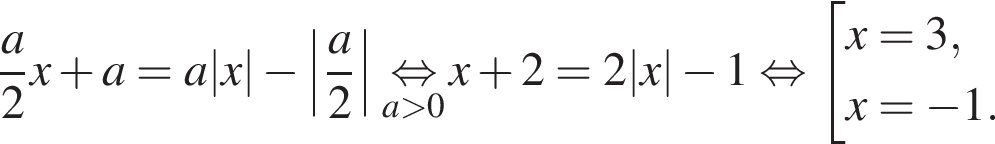

 График
График 



 или
или 
