
Радиус основания конуса равен 6, а его высота равна 8. Плоскость сечения содержит вершину конуса и хорду основания, длина которой равна 4.
а) Докажите, что сечение является равнобедренным остроугольным треугольником.
б) Найдите расстояние от центра основания конуса до плоскости сечения.
Решение. а) Сечение конуса плоскостью, содержащей его вершину S и хорду AB = 4, — треугольник ASB.
Две стороны сечения — это образующие конуса. Они равны, поэтому треугольник SAB равнобедренный. В равных прямоугольных треугольниках SOA и SOB, где O — центр основания конуса, OA = OB = 6, SO = 8, откуда

Тогда в треугольнике SAB угол S наименьший (поскольку лежит против меньшей стороны), а следовательно, острый. Два других угла равны между собой, поэтому тоже острые. Таким образом, треугольник SAB остроугольный.
б) Пусть SH — высота и медиана равнобедренного треугольника ASB,  Тогда отрезок OH — высота и медиана равнобедренного треугольника AOB,
Тогда отрезок OH — высота и медиана равнобедренного треугольника AOB,

Прямые SH и OH перпендикулярны прямой AB, поэтому плоскость SOH перпендикулярна плоскости ASB. Следовательно, расстояние от точки O до плоскости ASB равно высоте OM прямоугольного треугольника SOH, проведённой к гипотенузе:

Ответ: ![]()
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) ИЛИ имеется верное доказательство утверждения пункта а), и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а), ИЛИ при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | 1 |
| Решение не соответствует ни одному из критериев, приведённых выше | 0 |
| Максимальный балл | 3 |
 — треугольник ASB. Две стороны сечения — это образующие конуса. Они равны, поэтому треугольник SAB равнобедренный. В равных прямоугольных треугольниках SOA и SOB, где О — центр основания конуса,
— треугольник ASB. Две стороны сечения — это образующие конуса. Они равны, поэтому треугольник SAB равнобедренный. В равных прямоугольных треугольниках SOA и SOB, где О — центр основания конуса, 
 откуда
откуда 
 Тогда отрезок ОН — высота и медиана равнобедренного треугольника AOB,
Тогда отрезок ОН — высота и медиана равнобедренного треугольника AOB, 


 Каждое боковое ребро пирамиды наклонено к основанию под углом 60°.
Каждое боковое ребро пирамиды наклонено к основанию под углом 60°. Чтобы найти радиус окружности, описанной вокруг трапеции, удалим мысленно одну из вершин меньшего основания и найдем радиус окружности, описанной вокруг треугольника, вершинами которого являются три оставшиеся вершины трапеции.
Чтобы найти радиус окружности, описанной вокруг трапеции, удалим мысленно одну из вершин меньшего основания и найдем радиус окружности, описанной вокруг треугольника, вершинами которого являются три оставшиеся вершины трапеции.  Диагональ
Диагональ  Значит, окружность описана около треугольника со сторонами 25, 15, 20. Он прямоугольный, значит, центр описанной окружности трапеции находится на большем основании, а ее радиус R = 12,5.
Значит, окружность описана около треугольника со сторонами 25, 15, 20. Он прямоугольный, значит, центр описанной окружности трапеции находится на большем основании, а ее радиус R = 12,5. Тогда объем пирамиды
Тогда объем пирамиды 
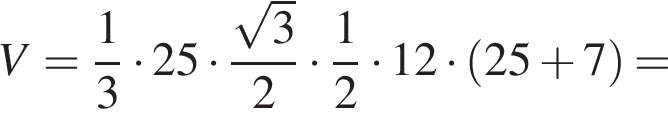





 SG = 1. Радиус, проведенный в точку касания, перпендикулярен касательной, поэтому треугольник OGS прямоугольный. По теореме Пифагора найдем квадрат его гипотенузы:
SG = 1. Радиус, проведенный в точку касания, перпендикулярен касательной, поэтому треугольник OGS прямоугольный. По теореме Пифагора найдем квадрат его гипотенузы: 

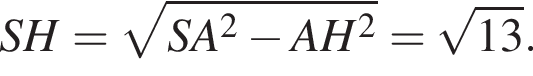



 то есть
то есть 


 где R — радиус основания, H — высота цилиндра. В данном случае
где R — радиус основания, H — высота цилиндра. В данном случае  поэтому
поэтому  откуда и следует требуемое.
откуда и следует требуемое.

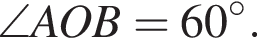 Треугольник AOB равноcтороний, следовательно,
Треугольник AOB равноcтороний, следовательно, 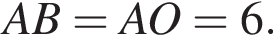
 как образующие конуса. Треугольник равнобедренный, значит, его углы при основании острые. Но
как образующие конуса. Треугольник равнобедренный, значит, его углы при основании острые. Но 

 Таким образом,
Таким образом,  поэтому точка P принадлежит кругу с центром B и радиусом BC. В обратную сторону: каждая точка круга с центром B, радиусом BC, и лежащего во второй плоскости, принадлежит шару. Таким образом, сечение есть круг.
поэтому точка P принадлежит кругу с центром B и радиусом BC. В обратную сторону: каждая точка круга с центром B, радиусом BC, и лежащего во второй плоскости, принадлежит шару. Таким образом, сечение есть круг. OB — расстояние между плоскостями, равное 2.
OB — расстояние между плоскостями, равное 2.
 высота
высота  а радиус вписанной окружности
а радиус вписанной окружности  Значит, площадь трапеции
Значит, площадь трапеции 
 Тогда площадь поверхности
Тогда площадь поверхности 







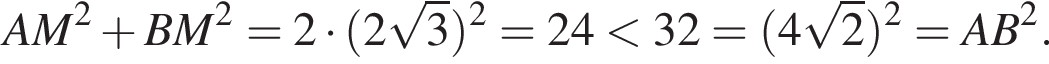




 Поэтому расстояния от центров оснований до хорд равны
Поэтому расстояния от центров оснований до хорд равны 



 поэтому
поэтому  где x — хорда AC. Проведем OH перпендикулярно AC. В силу того, что треугольник ACO равнобедренный, точка H также будет являться серединой AC. Тогда из прямоугольного треугольника, у которого гипотенуза — радиус OC, а один катет — половина этой хорды, находим второй катет OH по теореме Пифагора.
где x — хорда AC. Проведем OH перпендикулярно AC. В силу того, что треугольник ACO равнобедренный, точка H также будет являться серединой AC. Тогда из прямоугольного треугольника, у которого гипотенуза — радиус OC, а один катет — половина этой хорды, находим второй катет OH по теореме Пифагора. 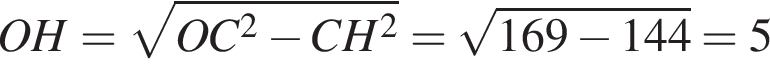

 поэтому
поэтому  значит, ABCD — квадрат.
значит, ABCD — квадрат. Поскольку
Поскольку  как угол, опирающийся на диаметр,
как угол, опирающийся на диаметр, 

 т. е.
т. е. 



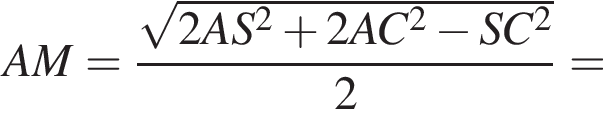
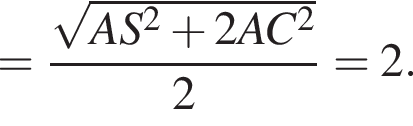






 Тогда отрезок NM лежит в плоскости yNz и
Тогда отрезок NM лежит в плоскости yNz и  Тогда скалярное произведение этих векторов равно нулю. Поскольку эти векторы ненулевые, они взаимно перпендикулярны.
Тогда скалярное произведение этих векторов равно нулю. Поскольку эти векторы ненулевые, они взаимно перпендикулярны. Тогда
Тогда

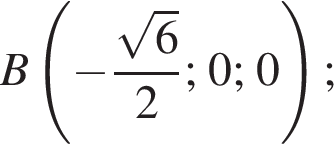


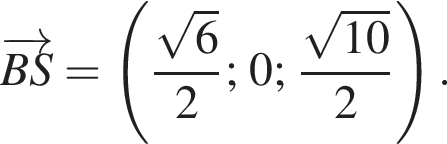




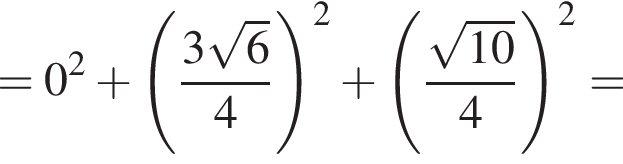



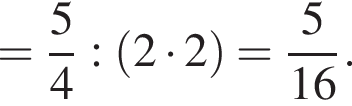

















 а радиус основания равен r. Найдем координаты точек A, B и C1:
а радиус основания равен r. Найдем координаты точек A, B и C1:









 а на окружности другого основания —
а на окружности другого основания — 

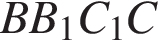 — прямоугольник, поэтому угол между прямыми
— прямоугольник, поэтому угол между прямыми  :
:
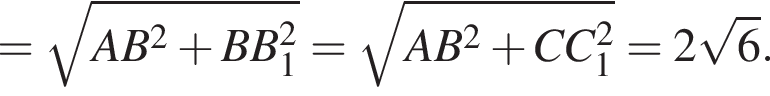






 поскольку опирается на него. CB является проекцией C1B. Тогда C1B перпендикулярно AB по теореме о трёх перпендикулярах, то есть
поскольку опирается на него. CB является проекцией C1B. Тогда C1B перпендикулярно AB по теореме о трёх перпендикулярах, то есть 
 Тогда по теореме Пифагора для треугольника ABC гипотенуза
Тогда по теореме Пифагора для треугольника ABC гипотенуза  Следовательно,
Следовательно, 
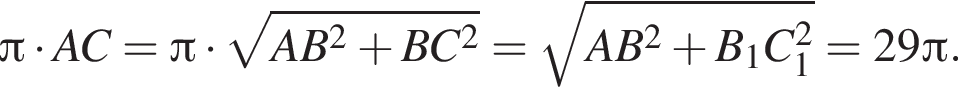


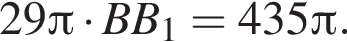





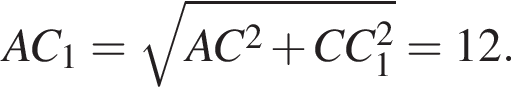 Таким образом, гипотенуза AC1 прямоугольного треугольника AB1C1 вдвое больше катета. Следовательно,
Таким образом, гипотенуза AC1 прямоугольного треугольника AB1C1 вдвое больше катета. Следовательно,  а искомый
а искомый 


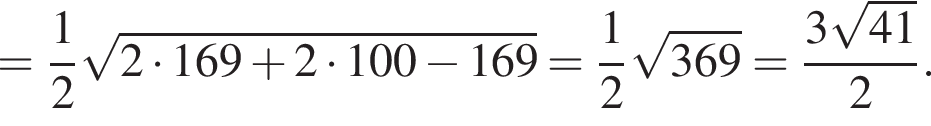







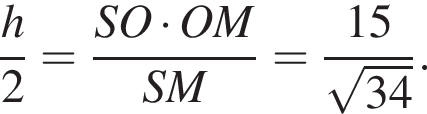


 — прямой.
— прямой.
















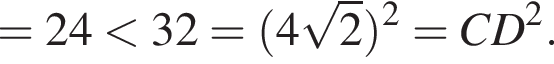


 а сторона основания
а сторона основания  Отсюда
Отсюда




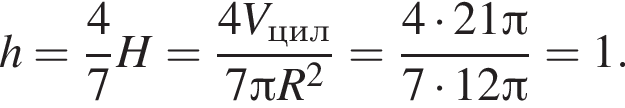





 Пусть эти образующие взаимно перпендикулярны. Соединим точки А и В, в равнобедренном прямоугольном треугольнике SAB гипотенуза
Пусть эти образующие взаимно перпендикулярны. Соединим точки А и В, в равнобедренном прямоугольном треугольнике SAB гипотенуза  Поскольку полученная длина хорды АВ меньше диаметра окружности, точки требуемым образом выбрать можно (см. прим.), потому искомое сечение — равнобедренный треугольник SAB с основанием AB, равным
Поскольку полученная длина хорды АВ меньше диаметра окружности, точки требуемым образом выбрать можно (см. прим.), потому искомое сечение — равнобедренный треугольник SAB с основанием AB, равным  и боковыми сторонами SA и SB, равными 13.
и боковыми сторонами SA и SB, равными 13.
 где
где 








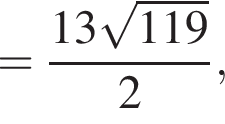







 где h — расстояние от точки A до плоскости SBC. Расстояние от точки O до плоскости SBC равно
где h — расстояние от точки A до плоскости SBC. Расстояние от точки O до плоскости SBC равно  Далее имеем:
Далее имеем: 
 и
и 
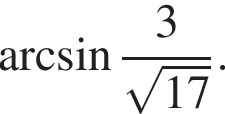



 и точка касания сферы с серединой ребра
и точка касания сферы с серединой ребра  удовлетворяют соответственно уравнениям:
удовлетворяют соответственно уравнениям:

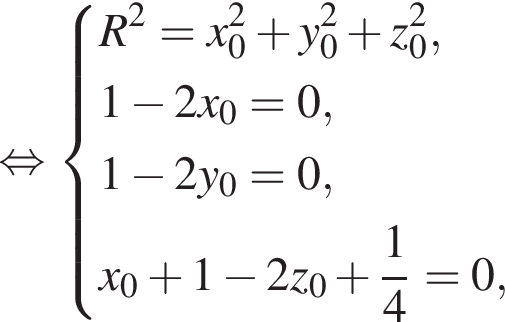


 то есть
то есть 




 ON = 3,
ON = 3,  Таким образом, в равнобедренном треугольнике MRS высота
Таким образом, в равнобедренном треугольнике MRS высота  следовательно, треугольник тупоугольный.
следовательно, треугольник тупоугольный.



 Таким образом,
Таким образом,

 а значит,
а значит, 


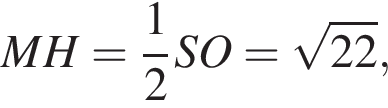





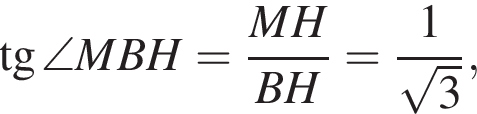

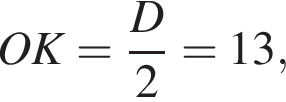






 Предоставляем читателю возможность самостоятельно решить задачу для этого случая.
Предоставляем читателю возможность самостоятельно решить задачу для этого случая. В цилиндре расположены два конуса: первый с вершиной F, основанием которого является круг основания с центром O1, второй — с вершиной P, основанием которого является круг основания с центром O2.
В цилиндре расположены два конуса: первый с вершиной F, основанием которого является круг основания с центром O1, второй — с вершиной P, основанием которого является круг основания с центром O2. В основаниях цилиндра и плоскости окружности пересечения конусов проведем три параллельных диаметра A1B1, A2B2 и AB соответственно. Рассмотрим сечение цилиндра плоскостью A1A2B2B1. В нем конусам будут соответствовать равнобедренные треугольники A1FB1 и A2PB2, боковые стороны которых пересекаются в точках
В основаниях цилиндра и плоскости окружности пересечения конусов проведем три параллельных диаметра A1B1, A2B2 и AB соответственно. Рассмотрим сечение цилиндра плоскостью A1A2B2B1. В нем конусам будут соответствовать равнобедренные треугольники A1FB1 и A2PB2, боковые стороны которых пересекаются в точках 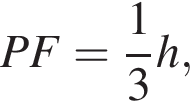
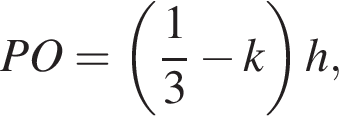










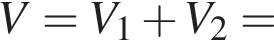




 Из подобия треугольников AO1O2 и ADH получаем
Из подобия треугольников AO1O2 и ADH получаем  то есть
то есть  Далее находим:
Далее находим:









 Угол SMO — линейный угол двугранного угла, образованного плоскостью SAB и плоскостью основания конуса. В прямоугольном треугольнике SMO находим:
Угол SMO — линейный угол двугранного угла, образованного плоскостью SAB и плоскостью основания конуса. В прямоугольном треугольнике SMO находим: 

 то
то 