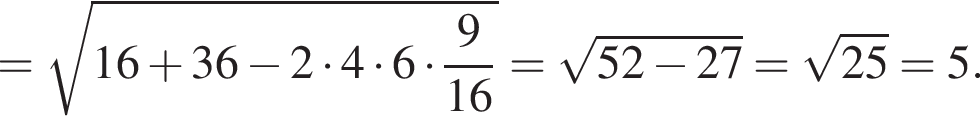В остроугольном треугольнике ABC проведены высоты AP и CQ.
а) Докажите, что угол PAC равен углу PQC.
б) Найдите радиус окружности, описанной около треугольника ABC, если известно, что PQ = 8 и ∠ABC = 60°.
Решение. а) Углы APC и AQC — прямые, значит, точки A, Q, P и C лежат на одной окружности с диаметром AC, а следовательно, равны и вписанные углы PAC и PQC этой окружности, опирающиеся на дугу PC, что и требовалось доказать.
б) Прямоугольные треугольники ABP и CBQ имеют общий угол ABC, следовательно, они подобны, откуда  или
или  но тогда и треугольники BAC и BPQ также подобны, причем коэффициент подобия равен
но тогда и треугольники BAC и BPQ также подобны, причем коэффициент подобия равен  откуда
откуда  Тогда радиус R окружности, описанной около треугольника ABC, равен
Тогда радиус R окружности, описанной около треугольника ABC, равен 
Ответ: ![]()
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) ИЛИ имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) ИЛИ при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | 1 |
| Решение не соответствует ни одному из критериев, приведённых выше | 0 |
| Максимальный балл | 3 |
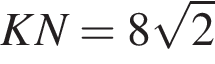 и ∠KMN = 45°.
и ∠KMN = 45°. или
или 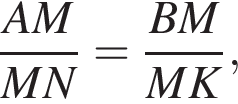 но тогда и треугольники KMN и BMA также подобны, причем коэффициент подобия равен
но тогда и треугольники KMN и BMA также подобны, причем коэффициент подобия равен  откуда
откуда 

 а
а 
 тогда
тогда  и
и  Треугольник BOC равнобедренный. Следовательно,
Треугольник BOC равнобедренный. Следовательно,









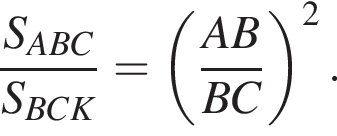 В треугольнике ABC имеем:
В треугольнике ABC имеем:

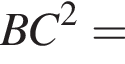



 тогда вокруг ACNM можно описать окружность, тогда
тогда вокруг ACNM можно описать окружность, тогда  как угол, опирающийся на одну дугу, что и требовалось доказать.
как угол, опирающийся на одну дугу, что и требовалось доказать. тогда
тогда 
























 поскольку является центральным углом, опирающимся на ту же дугу окружности, что и угол BAC. В равнобедренном треугольнике BOC получаем
поскольку является центральным углом, опирающимся на ту же дугу окружности, что и угол BAC. В равнобедренном треугольнике BOC получаем  а в прямоугольном треугольнике BAH получаем
а в прямоугольном треугольнике BAH получаем  Таким образом,
Таким образом, 
 Значит,
Значит,




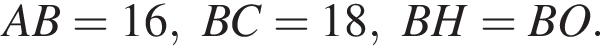


 а
а 
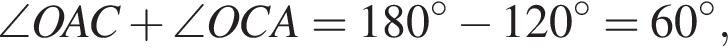 но величины
но величины  а значит,
а значит,  Тогда
Тогда 
 и
и  а значит,
а значит,  Углы
Углы  и
и  равны, поскольку опираются на одну и ту же дугу окружности, описанной около четырехугольника BDOE. Имеем:
равны, поскольку опираются на одну и ту же дугу окружности, описанной около четырехугольника BDOE. Имеем:


 Таким образом, треугольник ABC прямоугольный и его площадь равна
Таким образом, треугольник ABC прямоугольный и его площадь равна 
 Высоты BN и CM треугольника ABC пересекаются в точке H. Точка O — центр окружности, описанной около
Высоты BN и CM треугольника ABC пересекаются в точке H. Точка O — центр окружности, описанной около 
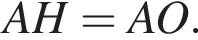
 если
если 

 Значит, треугольники ANM и ABC подобны с коэффициентом подобия
Значит, треугольники ANM и ABC подобны с коэффициентом подобия 
 Тогда
Тогда 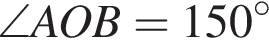 (центральный угол в два раза больше вписанного угла, опирающегося на ту же дугу). Тогда из суммы углов равнобедренного треугольника AOB:
(центральный угол в два раза больше вписанного угла, опирающегося на ту же дугу). Тогда из суммы углов равнобедренного треугольника AOB:  Поэтому
Поэтому 

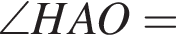

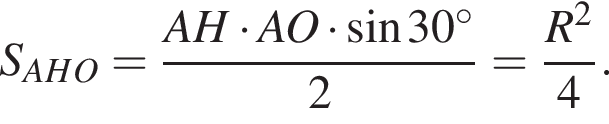 По теореме синусов для треугольника ABC:
По теореме синусов для треугольника ABC:

 воспользуемся формулой для расстояния от вершины до ортоцентра
воспользуемся формулой для расстояния от вершины до ортоцентра  Полученные величины равны, что и требовалось доказать.
Полученные величины равны, что и требовалось доказать.
 Тогда
Тогда 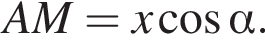 Сумма острых углов прямоугольного треугольника ACM равна 90°, поэтому
Сумма острых углов прямоугольного треугольника ACM равна 90°, поэтому  Тогда
Тогда  поскольку катет, лежащий против угла в 30°, в два раза меньше гипотенузы. Сумма острых углов прямоугольного треугольника AKB равна 90°, поэтому
поскольку катет, лежащий против угла в 30°, в два раза меньше гипотенузы. Сумма острых углов прямоугольного треугольника AKB равна 90°, поэтому  По теореме синусов для треугольника ABC:
По теореме синусов для треугольника ABC:  где R — радиус описанной вокруг треугольника ABC окружности. Откуда
где R — радиус описанной вокруг треугольника ABC окружности. Откуда  Ранее мы получили:
Ранее мы получили:  Следовательно,
Следовательно, 

 Четырехугольник MHNA вписан в окружность с диаметром AH, тогда по теореме синусов для треугольника MNA имеем:
Четырехугольник MHNA вписан в окружность с диаметром AH, тогда по теореме синусов для треугольника MNA имеем: 



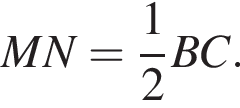 Подставляя, получаем:
Подставляя, получаем:
 Тогда
Тогда 
 Тогда
Тогда  Из доказанного в пункте a) имеем, что
Из доказанного в пункте a) имеем, что 


 Тогда
Тогда 

 Из доказанного в пункте a) имеем, что
Из доказанного в пункте a) имеем, что 


 Найдите B1C1.
Найдите B1C1.




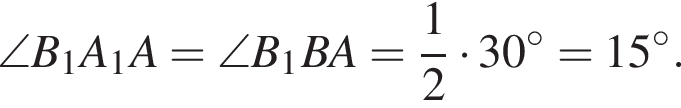



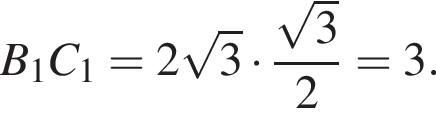

 AC = 1.
AC = 1.


 если К1 лежит вне окружности и
если К1 лежит вне окружности и  если К1 лежит внутри окружности. Значит, точки К и К1 совпадают, откуда следует, что НМ = МК.
если К1 лежит внутри окружности. Значит, точки К и К1 совпадают, откуда следует, что НМ = МК. значит, треугольник КСВ — равнобедренный и прямоугольный. Отрезок ВК является диаметром окружности, поэтому
значит, треугольник КСВ — равнобедренный и прямоугольный. Отрезок ВК является диаметром окружности, поэтому 







 Поэтому треугольники AB1C1 и ABC подобны по двум пропорциональным сторонам и углу между ними, коэффициент подобия равен
Поэтому треугольники AB1C1 и ABC подобны по двум пропорциональным сторонам и углу между ними, коэффициент подобия равен 








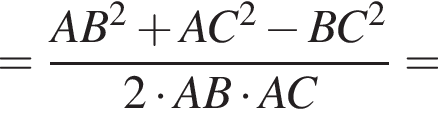












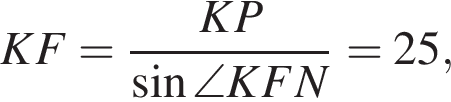




















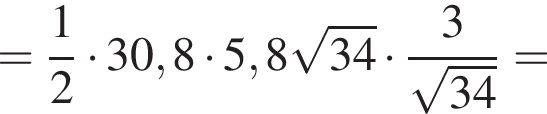




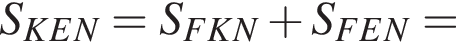






 отсюда
отсюда





 и четырёхугольник KLMO вписан в окружность.
и четырёхугольник KLMO вписан в окружность.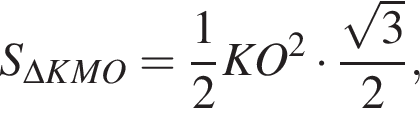 отсюда получаем:
отсюда получаем:
 По теореме синусов получаем:
По теореме синусов получаем: 
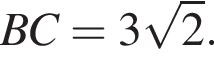



 Заметим, что
Заметим, что 
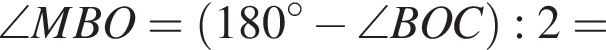

 следовательно, высота треугольника KBM равна R.
следовательно, высота треугольника KBM равна R. 

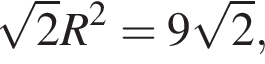 откуда
откуда  Это может быть только в том случае, если точки C и H совпадают. Следовательно, условию задачи удовлетворяет равнобедренный прямоугольный треугольник с гипотенузой AB = 6. Решение задачи приведено для общего случая.
Это может быть только в том случае, если точки C и H совпадают. Следовательно, условию задачи удовлетворяет равнобедренный прямоугольный треугольник с гипотенузой AB = 6. Решение задачи приведено для общего случая.
 следовательно,
следовательно, 
 что и требовалось доказать.
что и требовалось доказать.
 Пусть BH = x, HD = y, тогда
Пусть BH = x, HD = y, тогда

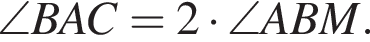
 поэтому получаем
поэтому получаем 
 Из треугольника АВС находим, что
Из треугольника АВС находим, что  AB = 8. Поскольку
AB = 8. Поскольку  получаем
получаем

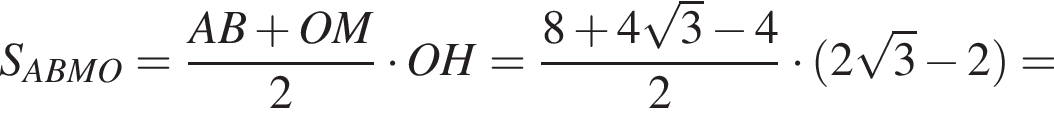



 и
и 


 следовательно,
следовательно,  Значит,
Значит, 


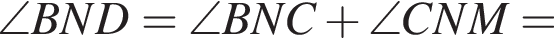







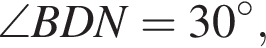 а значит,
а значит, 

 Тогда
Тогда  как вписанные, опирающиеся на одну и ту же дугу. Поэтому
как вписанные, опирающиеся на одну и ту же дугу. Поэтому  следовательно, прямые AB и CD параллельны.
следовательно, прямые AB и CD параллельны. Тогда
Тогда 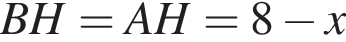 и DH = CH, поскольку треугольник CHD тоже равнобедренный. Находим:
и DH = CH, поскольку треугольник CHD тоже равнобедренный. Находим: 

 Найдите радиус описанной окружности треугольника ВКС, если сумма радиусов окружностей ω1 и ω2 равна
Найдите радиус описанной окружности треугольника ВКС, если сумма радиусов окружностей ω1 и ω2 равна 

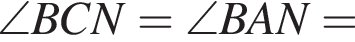






 следовательно,
следовательно,  Аналогично OH1 — радиус ω1 и
Аналогично OH1 — радиус ω1 и  тогда
тогда
 получаем, что
получаем, что 

 Тем самым точки B, C, K лежат на одной окружности с диаметром O1O2. Значит, ее радиус равен 5.
Тем самым точки B, C, K лежат на одной окружности с диаметром O1O2. Значит, ее радиус равен 5. Тогда равны и хорды AL = LB, а потому радиус LO — медиана и выcота треугольника ALB (поскольку точка O — середина стороны AB).
Тогда равны и хорды AL = LB, а потому радиус LO — медиана и выcота треугольника ALB (поскольку точка O — середина стороны AB). Заметим еще, что
Заметим еще, что  как вписанные углы, опирающиеся на одну и ту же дугу, откуда
как вписанные углы, опирающиеся на одну и ту же дугу, откуда  Тогда прямая KM является касательной к окружности, описанной около треугольника BMP.
Тогда прямая KM является касательной к окружности, описанной около треугольника BMP. откуда
откуда  а значит,
а значит,  Треугольники BOP и BCA подобны, поэтому
Треугольники BOP и BCA подобны, поэтому  следовательно,
следовательно, 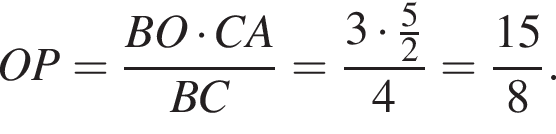
 и
и 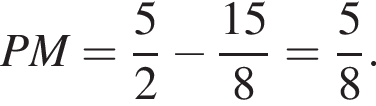 По свойству биссектрисы
По свойству биссектрисы  следовательно,
следовательно,  Тогда
Тогда 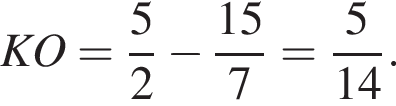





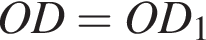 как радиусы, следовательно, медиана OH перпендикулярна хорде DD1.
как радиусы, следовательно, медиана OH перпендикулярна хорде DD1.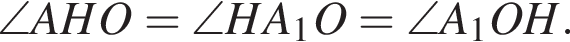
 и
и 
 Значит,
Значит,  и
и  откуда
откуда  Находим:
Находим: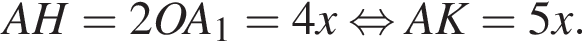












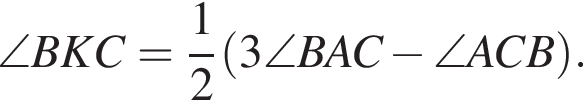
 а сумма расстояний от центра окружности O до сторон AC и BC равна
а сумма расстояний от центра окружности O до сторон AC и BC равна 
 тогда
тогда  по свойству угла между касательной и секущей. В треугольнике BCK по теореме о сумме углов получаем:
по свойству угла между касательной и секущей. В треугольнике BCK по теореме о сумме углов получаем: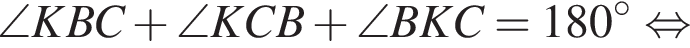





 и
и  Значит,
Значит, 




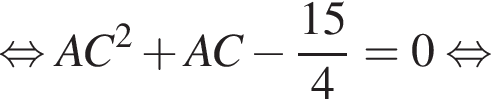
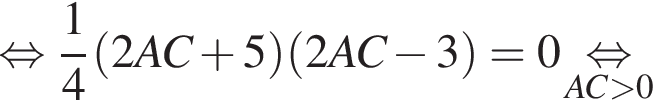


 тогда
тогда 

 Продолжение высоты ВТ треугольника АВС пересекает эту окружность в точке М.
Продолжение высоты ВТ треугольника АВС пересекает эту окружность в точке М.
 Тогда отрезки ML и AC параллельны, ведь они перпендикулярны хорде BM. Тогда
Тогда отрезки ML и AC параллельны, ведь они перпендикулярны хорде BM. Тогда  как накрест лежащие углы, но
как накрест лежащие углы, но  как вписанные углы, то есть
как вписанные углы, то есть  как вписанные и
как вписанные и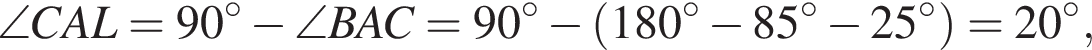










 тогда CL = 4, LB = 2. По теореме о пересекающихся хордах получаем:
тогда CL = 4, LB = 2. По теореме о пересекающихся хордах получаем:



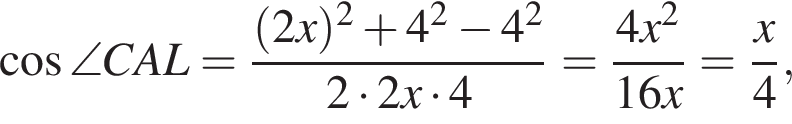








 то есть
то есть  Воспользуемся формулой Герона:
Воспользуемся формулой Герона:
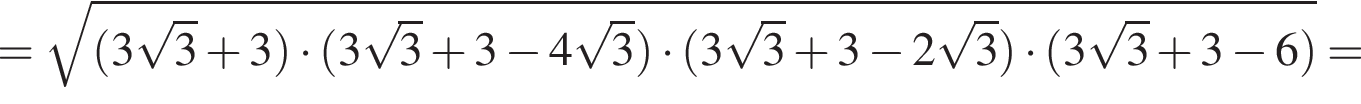




 Точка O — центр описанной окружности треугольника ABC. Вокруг треугольника AOC описана окружность, которая пересекает сторону BC в точке P.
Точка O — центр описанной окружности треугольника ABC. Вокруг треугольника AOC описана окружность, которая пересекает сторону BC в точке P.  откуда
откуда
 тогда
тогда
 откуда
откуда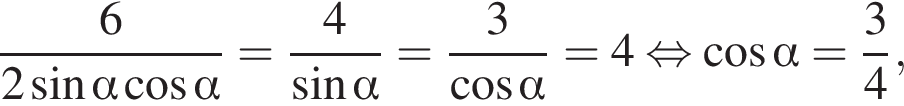


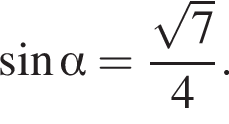 Далее последовательно получаем:
Далее последовательно получаем:



 поэтому
поэтому