Прямые, содержащие катеты AC и CB прямоугольного треугольника АСВ, являются общими внутренними касательными к окружностям радиусов
а) Докажите, что длина отрезка внутренней касательной, проведенной из вершины острого угла треугольника до одной из окружностей, равна половине периметра треугольника АСВ.
б) Найдите площадь треугольника АСВ.







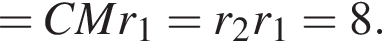



 где O1 — центр окружности с радиусом r1. При этом
где O1 — центр окружности с радиусом r1. При этом  тогда
тогда




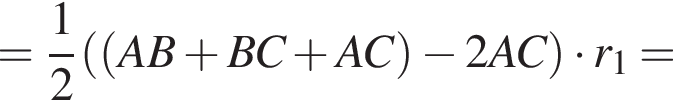



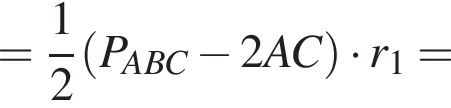

 следовательно,
следовательно,  Тогда
Тогда  Поэтому
Поэтому  что и требовалось доказать.
что и требовалось доказать.







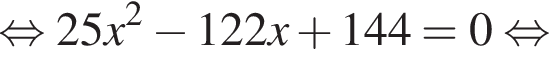
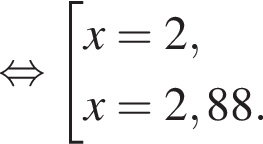

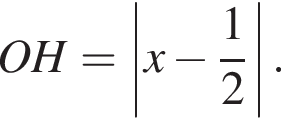 По теореме Пифагора в треугольнике QOH:
По теореме Пифагора в треугольнике QOH:




 тогда
тогда 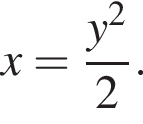 Площадь треугольника АВС равна сумме площадей треугольников BQC, AQC и AQB. Выразим площадь:
Площадь треугольника АВС равна сумме площадей треугольников BQC, AQC и AQB. Выразим площадь:





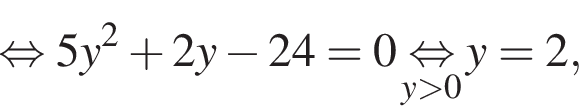


 Найденное значение радиуса второй окружности удовлетворяет условию пункта а) задачи, тем самым доказывая утверждение «радиус второй окружности меньше
Найденное значение радиуса второй окружности удовлетворяет условию пункта а) задачи, тем самым доказывая утверждение «радиус второй окружности меньше  (*),
(*),

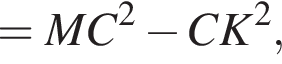






 Тогда
Тогда 
 и пусть
и пусть  тогда
тогда  По свойству секущих имеем:
По свойству секущих имеем:






 Из треугольника MKC:
Из треугольника MKC:
 Таким образом, получаем уравнение:
Таким образом, получаем уравнение: 


 С другой стороны из треугольника ABC по теореме косинусов имеем
С другой стороны из треугольника ABC по теореме косинусов имеем  Составим уравнение:
Составим уравнение: 










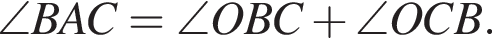

 Значит,
Значит,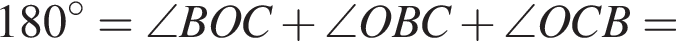









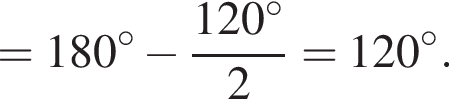
 поэтому точки B, O, I и C лежат на одной окружности.
поэтому точки B, O, I и C лежат на одной окружности.
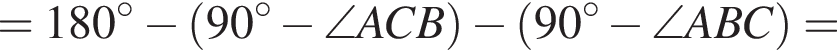



 поэтому точки B, O, I, H и C лежат на одной окружности.
поэтому точки B, O, I, H и C лежат на одной окружности. получаем
получаем  В равнобедренном треугольнике BOC имеем:
В равнобедренном треугольнике BOC имеем:

 Биссектриса угла треугольника лежит внутри угла, образованного медианой и высотой, исходящими из той же вершины, поэтому лучи BH, BI и BO пересекают дугу окружности в указанном на рисунке порядке. Четырёхугольник BOIH вписан в окружность, поэтому
Биссектриса угла треугольника лежит внутри угла, образованного медианой и высотой, исходящими из той же вершины, поэтому лучи BH, BI и BO пересекают дугу окружности в указанном на рисунке порядке. Четырёхугольник BOIH вписан в окружность, поэтому



 следовательно, точки A, B1, O и C1 лежат на одной окружности.
следовательно, точки A, B1, O и C1 лежат на одной окружности. как радиусы описанных окружностей около равных треугольников. Значит, треугольники AO1C1 и C1O2B равны. Кроме того, треугольник O2C1O1 также равен этим треугольникам, поскольку
как радиусы описанных окружностей около равных треугольников. Значит, треугольники AO1C1 и C1O2B равны. Кроме того, треугольник O2C1O1 также равен этим треугольникам, поскольку
 Аналогично
Аналогично 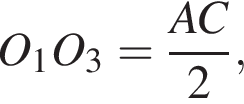
 поэтому треугольник O1O2O3 подобен треугольнику ABC с коэффициентом
поэтому треугольник O1O2O3 подобен треугольнику ABC с коэффициентом 
 поэтому
поэтому  Значит, r = 3. Искомый радиус равен
Значит, r = 3. Искомый радиус равен 











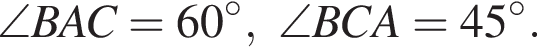

 но и
но и 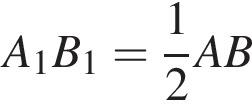 как средняя линия треугольника АВС. Поэтому четырёхугольник
как средняя линия треугольника АВС. Поэтому четырёхугольник  — равнобедренная трапеция, вокруг неё можно описать окружность, а значит, точки
— равнобедренная трапеция, вокруг неё можно описать окружность, а значит, точки 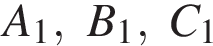 и H лежат на одной окружности. Что и требовалось доказать.
и H лежат на одной окружности. Что и требовалось доказать.
 Кроме того, из п. а)
Кроме того, из п. а) 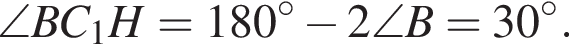 Следовательно,
Следовательно, 




 и
и  Тогда по теореме синусов для каждого из них имеем:
Тогда по теореме синусов для каждого из них имеем:

 откуда
откуда  Поскольку
Поскольку  сумма противоположных углов четырехугольника
сумма противоположных углов четырехугольника 












 где p — полупериметр треугольника, a — сторона, которой касается окружность. Таким образом,
где p — полупериметр треугольника, a — сторона, которой касается окружность. Таким образом,

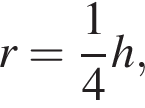 тогда
тогда  Найдем CH по теореме Пифагора, получим, что
Найдем CH по теореме Пифагора, получим, что  Тогда
Тогда

 Поскольку I — точка пересечения биссектрис треугольника ABC, получаем, что
Поскольку I — точка пересечения биссектрис треугольника ABC, получаем, что  Дуга BC окружности S2, не содержащая точки I, вдвое больше вписанного в эту окружность угла BIC,
Дуга BC окружности S2, не содержащая точки I, вдвое больше вписанного в эту окружность угла BIC,  Сумма углов при вершинах A и O четырехугольника ABOC равна 180°, значит, этот четырехугольник вписанный. Следовательно, точка O лежит на окружности, описанной около треугольника ABC.
Сумма углов при вершинах A и O четырехугольника ABOC равна 180°, значит, этот четырехугольник вписанный. Следовательно, точка O лежит на окружности, описанной около треугольника ABC.





 Следовательно,
Следовательно, 
 и
и  Точки M и N — середины сторон AB и AC соответственно.
Точки M и N — середины сторон AB и AC соответственно. 
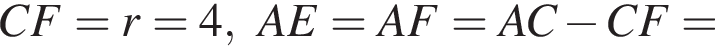




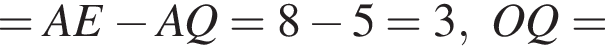








 и
и  проведённой из вершины L. Высота QT этого равнобедренного треугольника, опущенная на основание, является медианой, значит,
проведённой из вершины L. Высота QT этого равнобедренного треугольника, опущенная на основание, является медианой, значит,
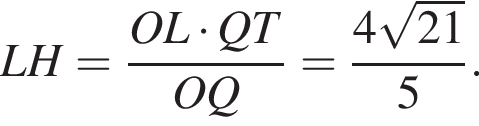


 поэтому
поэтому 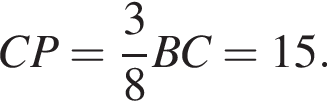






 Значит,
Значит,




 Следовательно,
Следовательно, 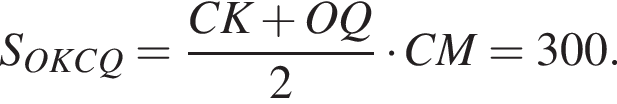

 а центр окружности лежит на высоте к стороне BC.
а центр окружности лежит на высоте к стороне BC. По теореме о секущей и касательной,
По теореме о секущей и касательной,


 как отрезки касательных, проведённых к окружности из одной точки. Значит,
как отрезки касательных, проведённых к окружности из одной точки. Значит,  и треугольник ABC равнобедренный.
и треугольник ABC равнобедренный. Центр окружности, вписанной в угол, лежит на биссектрисе угла. Значит, точка O лежит на биссектрисе угла B треугольника ABC. Поскольку треугольник ABC равнобедренный, биссектриса угла B перпендикулярна стороне AC, и тогда O — точка пересечения высот треугольника ABC, то есть
Центр окружности, вписанной в угол, лежит на биссектрисе угла. Значит, точка O лежит на биссектрисе угла B треугольника ABC. Поскольку треугольник ABC равнобедренный, биссектриса угла B перпендикулярна стороне AC, и тогда O — точка пересечения высот треугольника ABC, то есть 


 — радиус окружности. Рассмотрим прямоугольные треугольники ACQ и ABQ. Из
— радиус окружности. Рассмотрим прямоугольные треугольники ACQ и ABQ. Из 





 отсюда
отсюда 

 или
или 

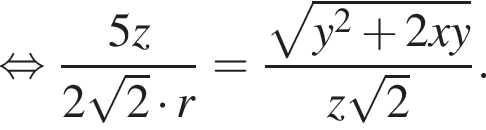

 :
:










 где r — искомый радиус,
где r — искомый радиус, откуда
откуда 









 значит, AF — медиана. Найдём её:
значит, AF — медиана. Найдём её:

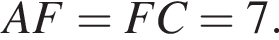

 то есть треугольник ABC равнобедренный.
то есть треугольник ABC равнобедренный.
 и прямая MN параллельна прямой BC. Отрезок BC равен 35.
и прямая MN параллельна прямой BC. Отрезок BC равен 35.














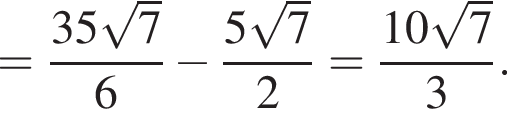


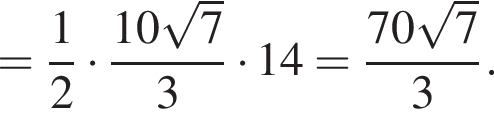
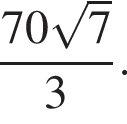



 тогда
тогда  Найдём BB1 по теореме косинусов:
Найдём BB1 по теореме косинусов:







 поскольку синусы смежных углов равны. Получаем:
поскольку синусы смежных углов равны. Получаем:








 и площадь треугольника АВ1С1 в четыре раза меньше площади четырёхугольника ВСВ1С1.
и площадь треугольника АВ1С1 в четыре раза меньше площади четырёхугольника ВСВ1С1.



 Теперь по теореме синусов из треугольника ABB1 получаем:
Теперь по теореме синусов из треугольника ABB1 получаем:


 поскольку синусы смежных углов равны.
поскольку синусы смежных углов равны.







 Так как C1A1 — медиана в прямоугольном треугольнике BC1C, то
Так как C1A1 — медиана в прямоугольном треугольнике BC1C, то 


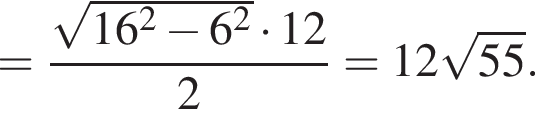

 Тогда по свойству медиан прямоугольного треугольника
Тогда по свойству медиан прямоугольного треугольника 





 Во второй окружности углы AOK и AМK являются вписанными, опирающимися на дугу AK, следовательно,
Во второй окружности углы AOK и AМK являются вписанными, опирающимися на дугу AK, следовательно, 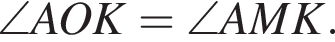 Получаем, что
Получаем, что 

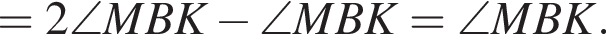


 то есть
то есть  Тогда
Тогда  а значит,
а значит, 
 Следовательно, треугольник MCN подобен треугольнику BCA с коэффициентом
Следовательно, треугольник MCN подобен треугольнику BCA с коэффициентом 

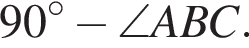 Таким образом, треугольники HMN и CAB подобны по двум углам. Что и требовалось доказать.
Таким образом, треугольники HMN и CAB подобны по двум углам. Что и требовалось доказать. а
а  Поэтому треугольники CMH и BNH подобны по двум углам, причем из пункта а) следует, что
Поэтому треугольники CMH и BNH подобны по двум углам, причем из пункта а) следует, что 
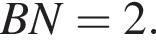













 CK = 8.
CK = 8.



 откуда следует, что
откуда следует, что 






 а радиус малой окружности равен
а радиус малой окружности равен  по теореме об угле между касательной и хордой. Аналогично
по теореме об угле между касательной и хордой. Аналогично  значит,
значит,  откуда следует, что хорды AB и MN параллельны. Следовательно, треугольники LAK и CMK и треугольники LBK и CNK подобны. Таким образом,
откуда следует, что хорды AB и MN параллельны. Следовательно, треугольники LAK и CMK и треугольники LBK и CNK подобны. Таким образом,
 Что и требовалось доказать.
Что и требовалось доказать. и
и  тогда
тогда  Точка O1 — центр малой окружности, значит, радиус O1C перпендикулярен хорде MN. Находим:
Точка O1 — центр малой окружности, значит, радиус O1C перпендикулярен хорде MN. Находим: 
 откуда получаем уравнение:
откуда получаем уравнение:


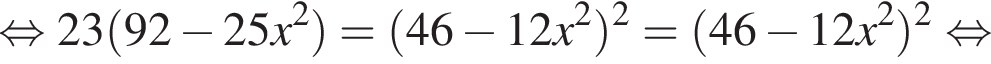


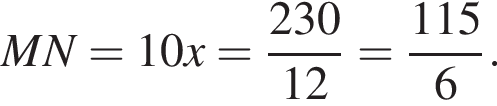
 откуда
откуда  Положим CN = 4x, тогда по теореме о касательной и секущей:
Положим CN = 4x, тогда по теореме о касательной и секущей:  следовательно,
следовательно,  В треугольнике NCK известны все стороны, применим теорему косинусов:
В треугольнике NCK известны все стороны, применим теорему косинусов: 


 по теореме об угле между касательной и хордой. Значит,
по теореме об угле между касательной и хордой. Значит, 




 а потому точка O1 лежит на луче EF и внутри треугольника ACD. Следовательно, точка O1 лежит на отрезке EF. Аналогично и точка O2 лежит на отрезке EF.
а потому точка O1 лежит на луче EF и внутри треугольника ACD. Следовательно, точка O1 лежит на отрезке EF. Аналогично и точка O2 лежит на отрезке EF.
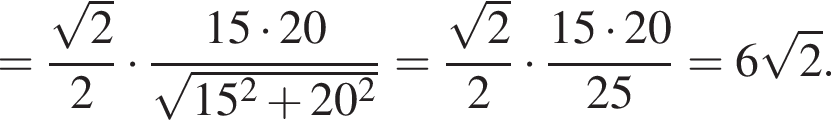


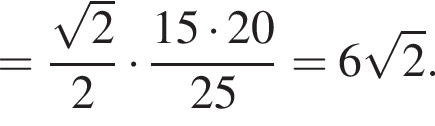




 отрезки O1H и O3M — радиусы окружностей, проведенные в точки касания с основанием AC. Тогда
отрезки O1H и O3M — радиусы окружностей, проведенные в точки касания с основанием AC. Тогда

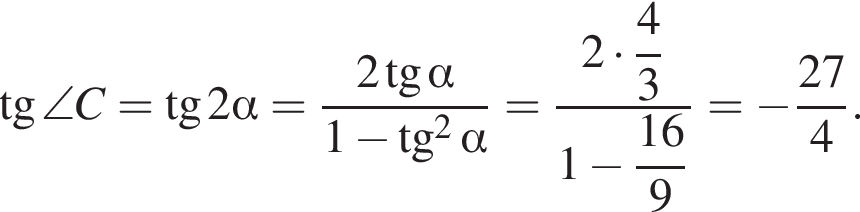

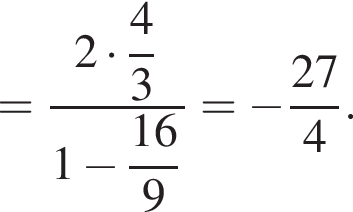
 Что и требовалось доказать.
Что и требовалось доказать.

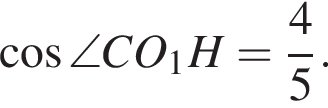
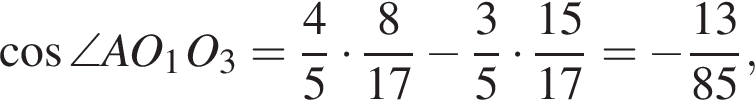





 По условию MS = MT, следовательно, MK = ME и SE = TK. Треугольники EKT и KES равны по катету и гипотенузе, значит,
По условию MS = MT, следовательно, MK = ME и SE = TK. Треугольники EKT и KES равны по катету и гипотенузе, значит,  откуда
откуда  Из этого следует, что точка M лежит вне окружности.
Из этого следует, что точка M лежит вне окружности. 

 и
и 


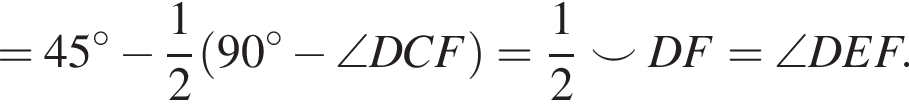








 Расстояние от точки С до отрезка O1O2 равно высоте треугольника CEF. Треугольник прямоугольный и равнобедренный, значит, расстояние равно половине гипотенузы EF, то есть
Расстояние от точки С до отрезка O1O2 равно высоте треугольника CEF. Треугольник прямоугольный и равнобедренный, значит, расстояние равно половине гипотенузы EF, то есть  Тогда
Тогда  следовательно, около четырёхугольника AOBO1 можно описать окружность.
следовательно, около четырёхугольника AOBO1 можно описать окружность.
 и
и  тогда треугольник AKO равнобедренный, откуда следует, что AK = KO. Найдем OK по формуле
тогда треугольник AKO равнобедренный, откуда следует, что AK = KO. Найдем OK по формуле  Получаем:
Получаем:
 откуда
откуда  Треугольник ALO1 равнобедренный, значит,
Треугольник ALO1 равнобедренный, значит,  Находим площадь четырёхугольника AOBO1
Находим площадь четырёхугольника AOBO1




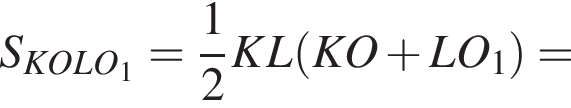






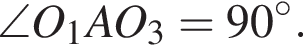 Аналогично O3С и O2B — высоты треугольника O1O2O3.
Аналогично O3С и O2B — высоты треугольника O1O2O3.

 Тогда
Тогда
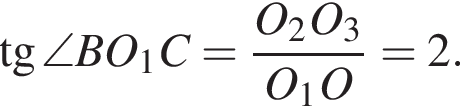 Значит,
Значит, 

















 что не зависит от положения точки D.
что не зависит от положения точки D.








 Поэтому треугольники O1DM и DO2N подобные. Следовательно,
Поэтому треугольники O1DM и DO2N подобные. Следовательно,  откуда
откуда  то есть
то есть 


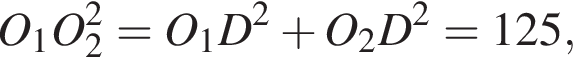 откуда
откуда 



 Опустим из P перпендикуляр PH на AC. Точка пересечения биссектрисы угла треугольника с серединным перпендикуляром к противолежащей стороне лежит на описанной окружности этого треугольника, поэтому отрезок PH — серединный перпендикуляр к стороне AC. Четырехугольник ABCP вписанный, значит,
Опустим из P перпендикуляр PH на AC. Точка пересечения биссектрисы угла треугольника с серединным перпендикуляром к противолежащей стороне лежит на описанной окружности этого треугольника, поэтому отрезок PH — серединный перпендикуляр к стороне AC. Четырехугольник ABCP вписанный, значит,



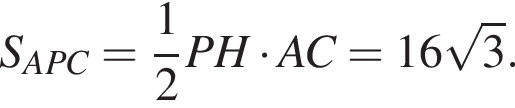
 выбрана точка Q такая, что SABQ : SACQ : SCBQ = 1 : 2 : 4. Прямые CQ и AQ пересекают стороны AB и BC соответственно в точках
выбрана точка Q такая, что SABQ : SACQ : SCBQ = 1 : 2 : 4. Прямые CQ и AQ пересекают стороны AB и BC соответственно в точках 





 следовательно, треугольники ACB и LKB подобны по двум углам. Из подобия следует, что
следовательно, треугольники ACB и LKB подобны по двум углам. Из подобия следует, что
 тогда
тогда 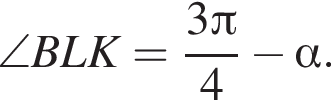 По теореме синусов имеем:
По теореме синусов имеем:





 то есть треугольник ABC равнобедренный.
то есть треугольник ABC равнобедренный. и
и  тогда
тогда  и
и  По теореме Менелая для треугольника BKC получаем:
По теореме Менелая для треугольника BKC получаем:



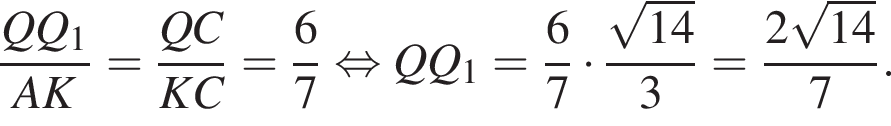










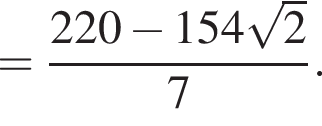

 значит,
значит,  Однако радиус OM перпендикулярен касательной AM, поэтому
Однако радиус OM перпендикулярен касательной AM, поэтому 





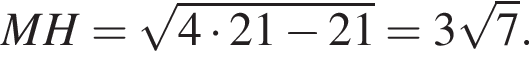 Следовательно,
Следовательно,  По теореме косинусов в треугольнике AMK:
По теореме косинусов в треугольнике AMK:
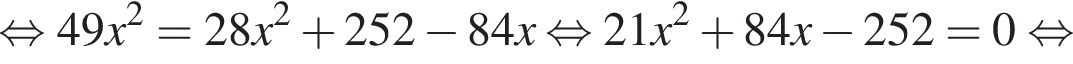

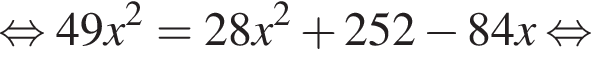








 тогда
тогда  как центральный угол. Отрезки BO и OC равны как радиусы. Следовательно, в равнобедренном треугольнике OBC
как центральный угол. Отрезки BO и OC равны как радиусы. Следовательно, в равнобедренном треугольнике OBC









