1. Тип 15 № 507258 

Классификатор алгебры: Неравенства с логарифмами по переменному основанию
Методы алгебры: Метод интервалов, Рационализация неравенств. Логарифмы
Кодификатор ФИПИ/Решу ЕГЭ: 2.2.9 Метод интервалов
Неравенства. Неравенства с логарифмами по переменному основанию, применение рационализации
i
Решите неравенство 
Решение. Решим неравенство методом рационализации:







Ответ: (−4; −3) ∪ (−1; 3).
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 2 |
| Обоснованно получен ответ, отличающийся от верного исключением точек, ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Ответ: (−4; −3) ∪ (−1; 3).
507258
(−4; −3) ∪ (−1; 3).
Классификатор алгебры: Неравенства с логарифмами по переменному основанию
Методы алгебры: Метод интервалов, Рационализация неравенств. Логарифмы
Кодификатор ФИПИ/Решу ЕГЭ: 2.2.9 Метод интервалов


 третий не дает корней.
третий не дает корней.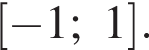



 совпадает со знаком выражения
совпадает со знаком выражения  Знак множителя
Знак множителя  совпадает со знаком выражения
совпадает со знаком выражения  которое на области определения неравенства всегда положительно.
которое на области определения неравенства всегда положительно.




 получаем:
получаем:
 то
то
 то
то



 Напомним, что области определения неравенство
Напомним, что области определения неравенство  равносильно неравенству
равносильно неравенству  :
:
















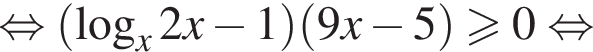
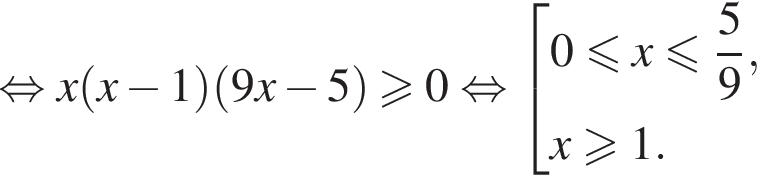







 получаем:
получаем: 




 получаем
получаем  или
или 














 при всех
при всех 
 или
или 







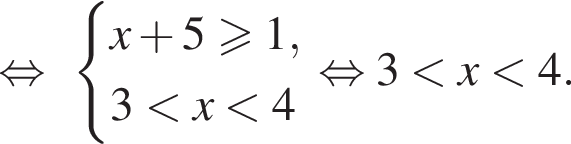
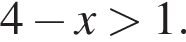




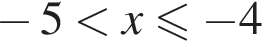 или
или 


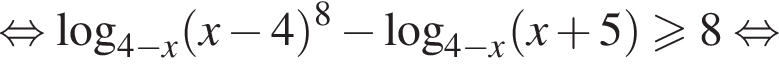





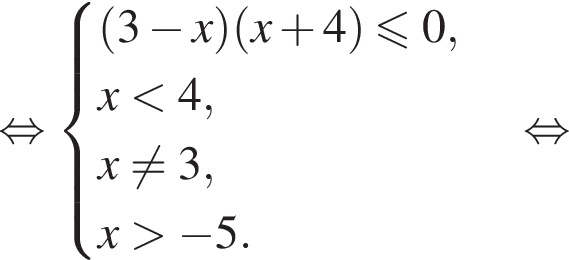











 Имеем:
Имеем:




 или
или 
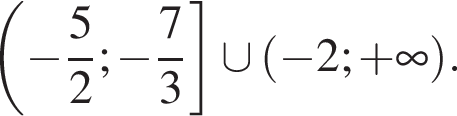
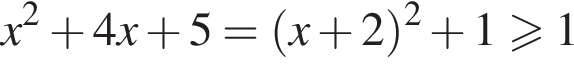 при любых значениях х. Значит, логарифм положителен, если его основание больше 1, т. е. при
при любых значениях х. Значит, логарифм положителен, если его основание больше 1, т. е. при  и отрицателен, если его основание меньше 1, если
и отрицателен, если его основание меньше 1, если 
 выражение 3x + 7 положительно, а при
выражение 3x + 7 положительно, а при  исходное неравенство равносильно неравенству
исходное неравенство равносильно неравенству  откуда
откуда 


 имеют одинаковые знаки. Поэтому при условиях
имеют одинаковые знаки. Поэтому при условиях 






 при любых значениях x. Значит, выражение
при любых значениях x. Значит, выражение  положительно при
положительно при  и не определено при
и не определено при  исходное неравенство равносильно неравенству
исходное неравенство равносильно неравенству 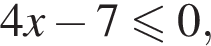 откуда
откуда  Таким образом, решение исходного неравенства:
Таким образом, решение исходного неравенства: 

 и
и  имеем:
имеем:





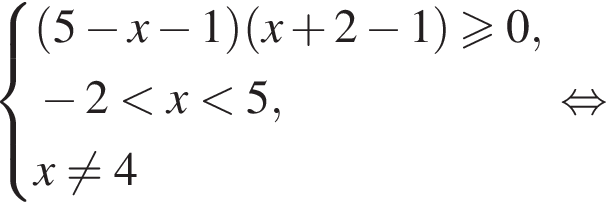

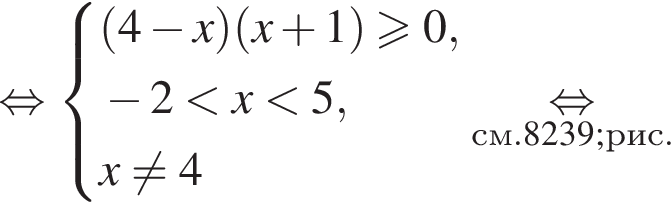













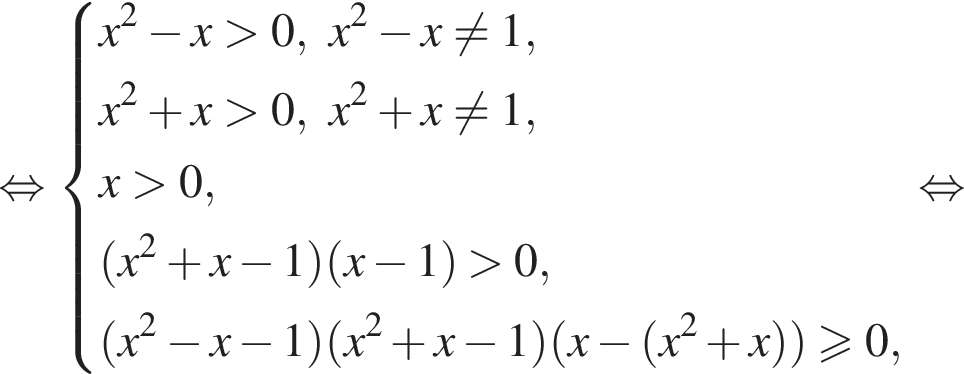





 следует, что
следует, что  поскольку основание этого логарифма больше 2, аргумент больше 1, причем аргумент меньше основания. Тогда для выполнения неравенства основание внешнего логарифма должно быть меньше 1, откуда
поскольку основание этого логарифма больше 2, аргумент больше 1, причем аргумент меньше основания. Тогда для выполнения неравенства основание внешнего логарифма должно быть меньше 1, откуда  при
при 


















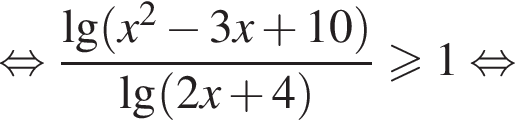
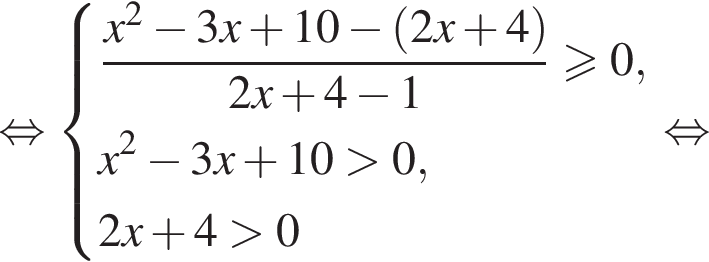

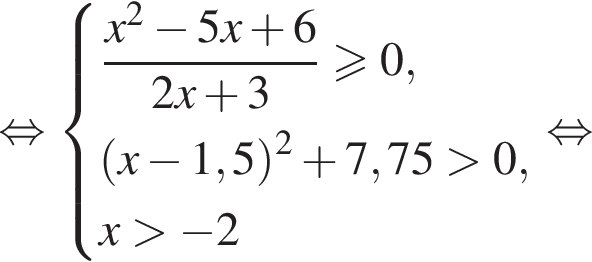
 в виде
в виде 
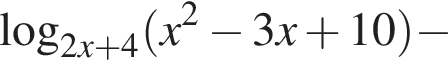

 на ОДЗ совпадает со знаком дроби
на ОДЗ совпадает со знаком дроби 






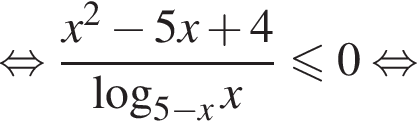







 Применим ее к обеим частям неравенства и воспользуемся методом рационализации:
Применим ее к обеим частям неравенства и воспользуемся методом рационализации:














 то есть при
то есть при 
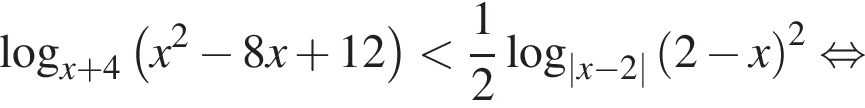










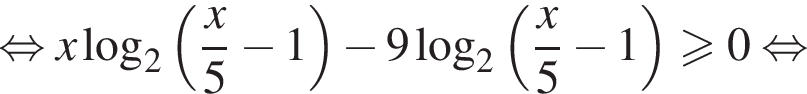





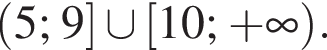

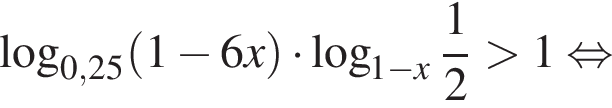






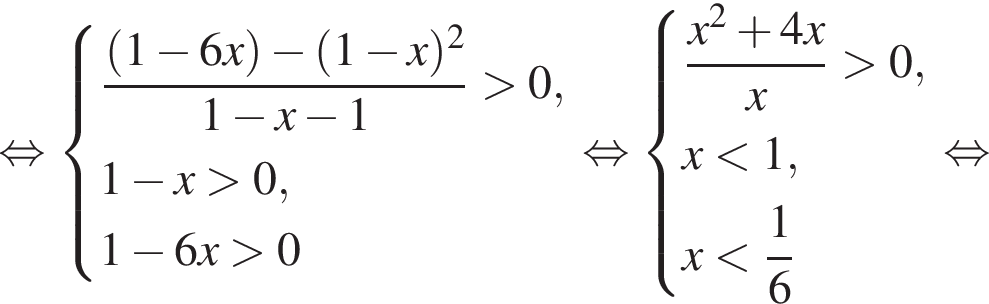







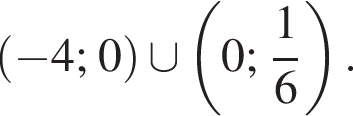

 тогда
тогда








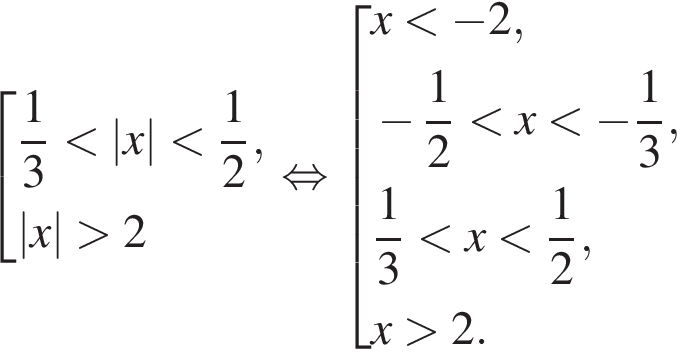














 тогда исходное неравенство принимает вид
тогда исходное неравенство принимает вид



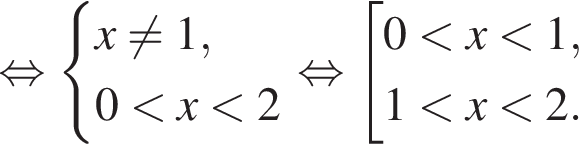




 сложим их, затем перейдем к основанию 6 и вычтем из полученной левой части правую часть неравенства; затем применим метод рационализации:
сложим их, затем перейдем к основанию 6 и вычтем из полученной левой части правую часть неравенства; затем применим метод рационализации:








 тогда
тогда







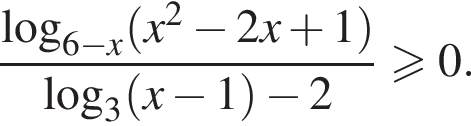

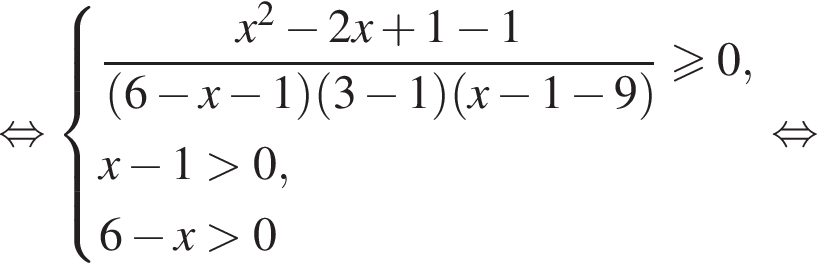







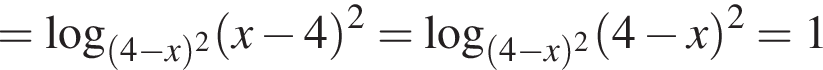



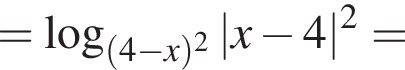
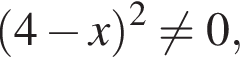
 Применим метод рационализации:
Применим метод рационализации:




















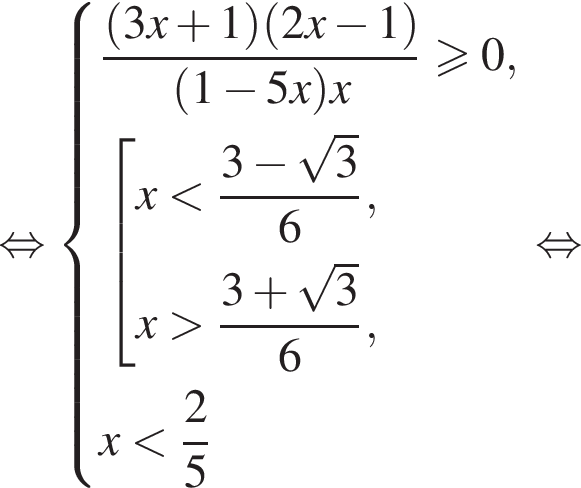

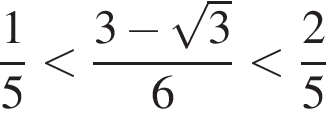 :
:






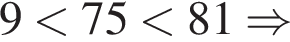





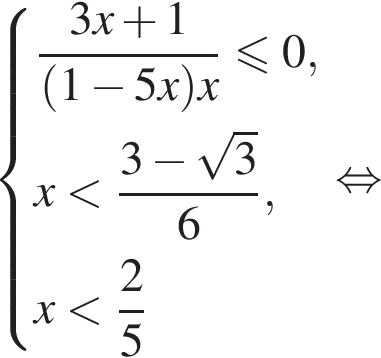





















 откуда
откуда  то есть
то есть  Полученное неравенство решим методом рационализации:
Полученное неравенство решим методом рационализации:
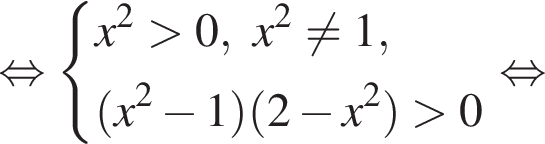








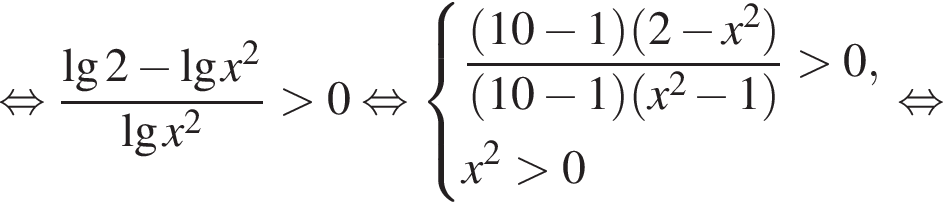



















 и
и  используя геометрический смысл модуля. Решение первого уравнения — множество точек числовой прямой, находящихся на расстоянии 1 от точки
используя геометрический смысл модуля. Решение первого уравнения — множество точек числовой прямой, находящихся на расстоянии 1 от точки  Это точки
Это точки  равна 4. Это точки
равна 4. Это точки 


 или
или 





 Тогда
Тогда

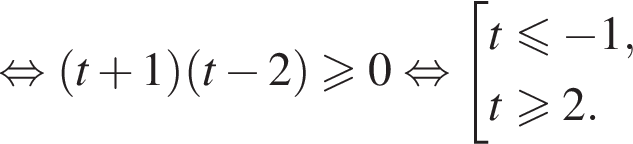





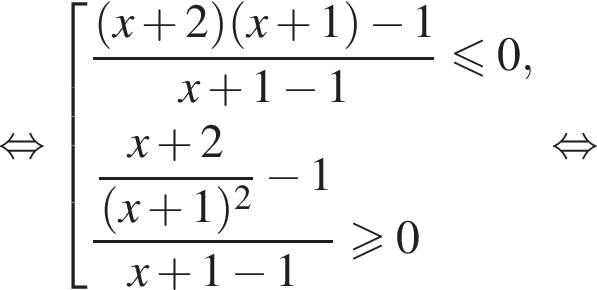

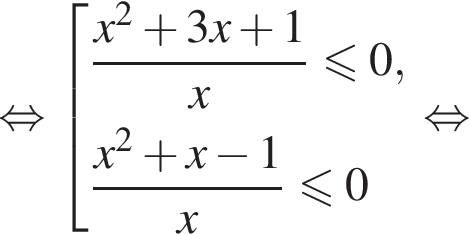
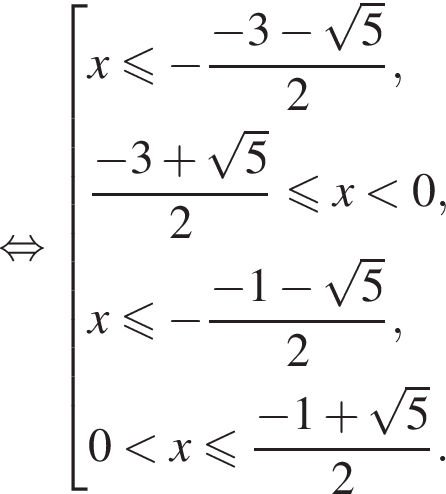
 или
или 









 а потому выражение в скобках положительно, и на него можно разделить. Далее применим метод рационализации:
а потому выражение в скобках положительно, и на него можно разделить. Далее применим метод рационализации:
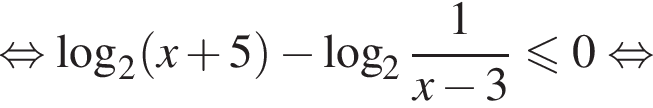







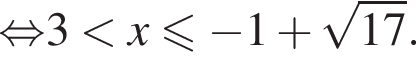








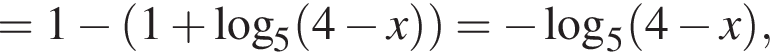
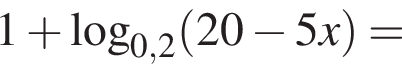






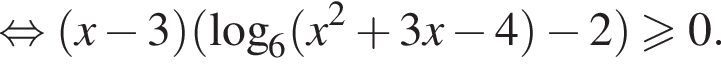
 и
и  совпадают, а потому исходное неравенство равносильно следующим:
совпадают, а потому исходное неравенство равносильно следующим:







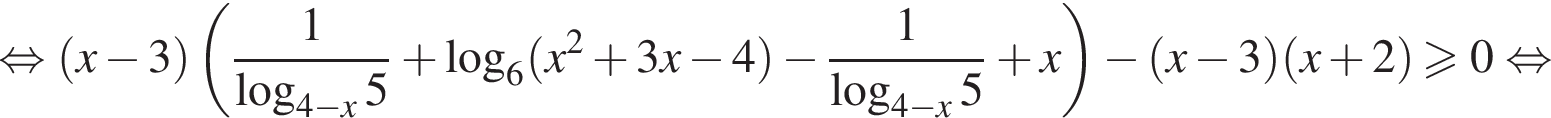






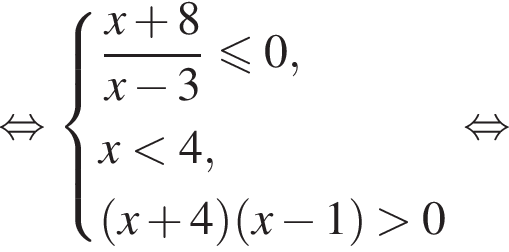











 что равносильно неравенству
что равносильно неравенству 



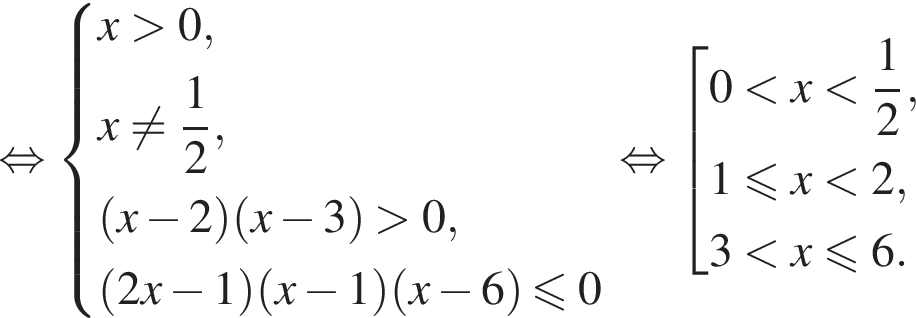






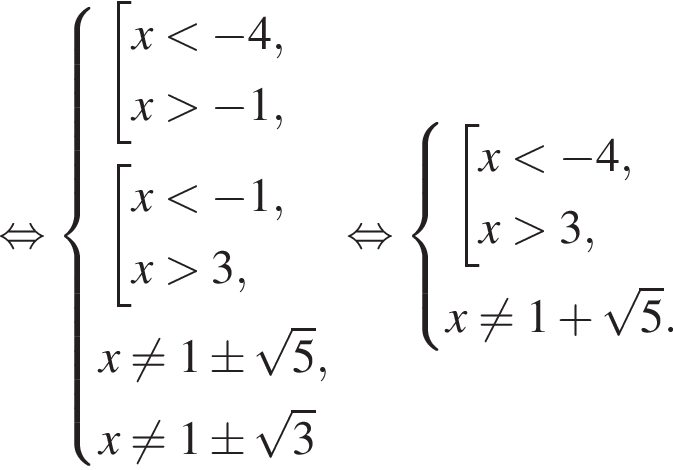



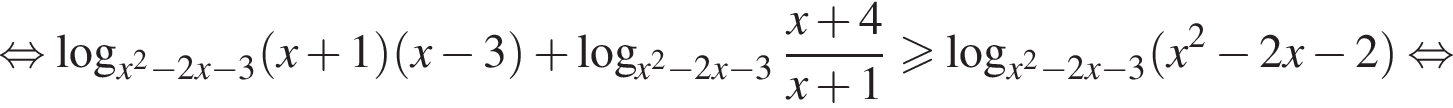



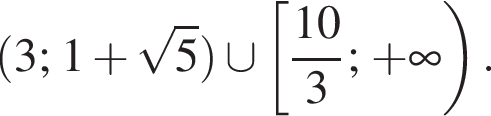

 На этом множестве справедливо тождество
На этом множестве справедливо тождество 
 тогда
тогда


