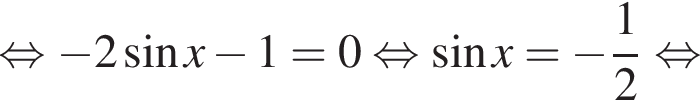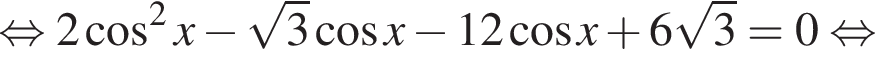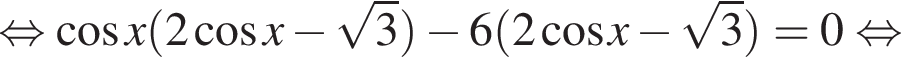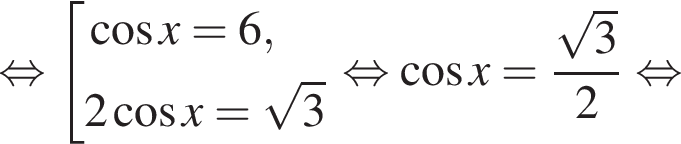1. Тип 13 № 515648 

Классификатор алгебры: Уравнения смешанного типа
Методы алгебры: Домножение на знаменатель с учётом ОДЗ
Кодификатор ФИПИ/Решу ЕГЭ:
Уравнения. Тригонометрия и логарифмы
i
а) Решите уравнение 
б) Найдите все корни этого уравнения, принадлежащие отрезку 
Решение. а)

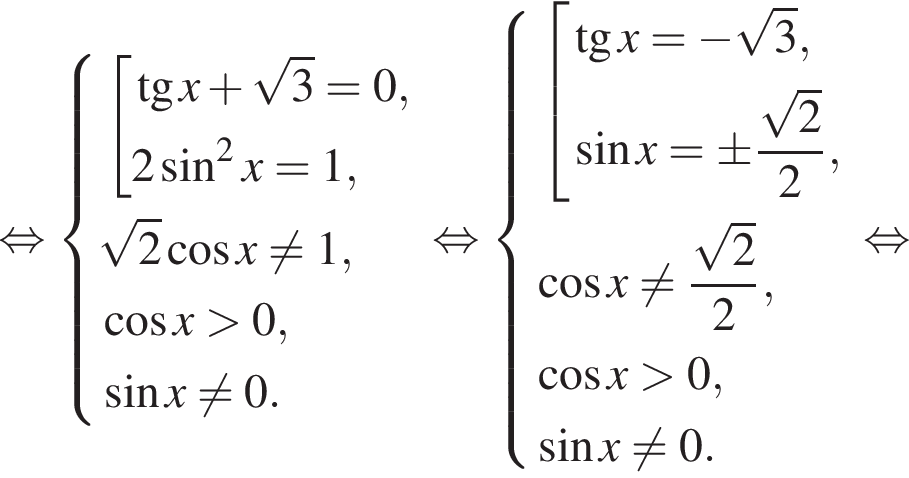



б) С помощью числовой окружности отберём корни, принадлежащие отрезку  Получим число
Получим число ![]()
Ответ: а)  б)
б) ![]()
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Ответ: а)  б)
б) 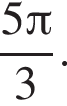
 б)
б) 515648
а)  б)
б) 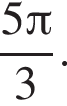
 б)
б) Классификатор алгебры: Уравнения смешанного типа
Методы алгебры: Домножение на знаменатель с учётом ОДЗ
Кодификатор ФИПИ/Решу ЕГЭ:




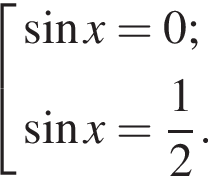
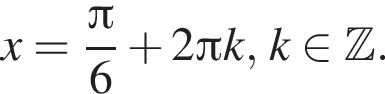

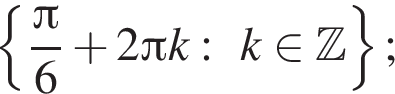 б)
б) 








 Получим числа:
Получим числа: 
 б)
б) 

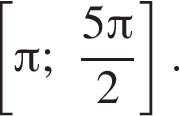

 то
то  откуда
откуда 
 то
то  откуда
откуда 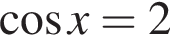 или
или 
 имеет корни
имеет корни  Учитывая, что
Учитывая, что  получаем:
получаем: 
 откуда
откуда  откуда
откуда  б)
б) 
 тогда
тогда  откуда
откуда 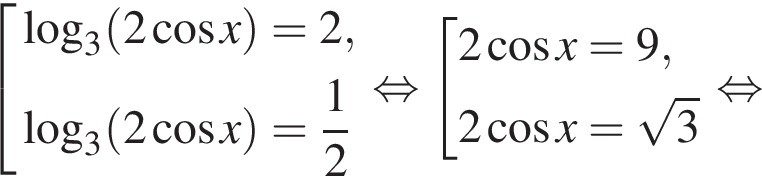




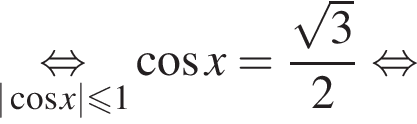


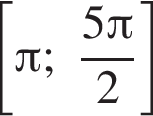 :
: б)
б)  при помощи тригонометрической окружности. Подходят:
при помощи тригонометрической окружности. Подходят: 

 Заметим, что выражение, стоящее под знаком логарифма, приравнено к положительному числу, поэтому исследовать ОДЗ не требуется.
Заметим, что выражение, стоящее под знаком логарифма, приравнено к положительному числу, поэтому исследовать ОДЗ не требуется. 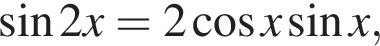 откуда получаем
откуда получаем  откуда
откуда  или
или 
 находим:
находим: 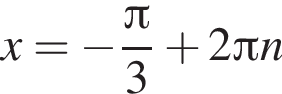 или
или 
 находим:
находим: 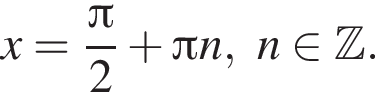
 Получим числа:
Получим числа:  б)
б)

 тогда имеем:
тогда имеем: 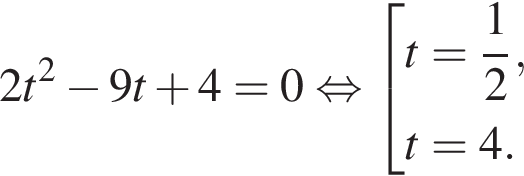



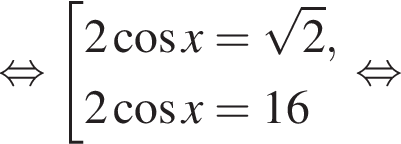




 Получим число
Получим число  б)
б) 

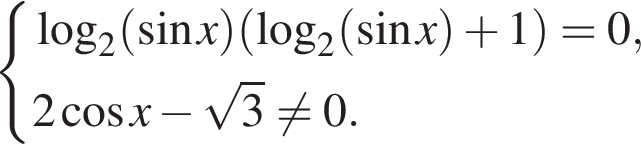
 Получаем:
Получаем: 
 получаем
получаем 

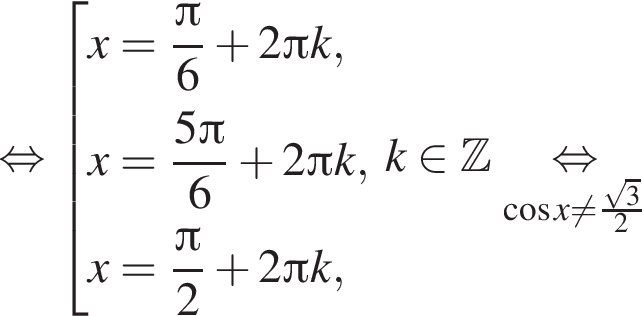

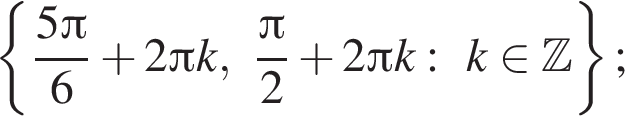 б)
б) 


 Заметим, что выражение, стоящее под знаком логарифма, приравнено к единице, поэтому исследовать ОДЗ не требуется.
Заметим, что выражение, стоящее под знаком логарифма, приравнено к единице, поэтому исследовать ОДЗ не требуется.  откуда получаем
откуда получаем  Обозначая
Обозначая  имеем:
имеем:



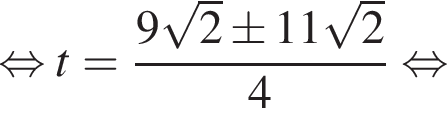

 корней не имеет, поскольку косинус не больше 1.
корней не имеет, поскольку косинус не больше 1.  находим:
находим:  или
или 

 б)
б) 
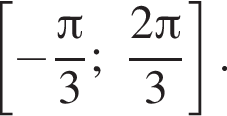
 тогда имеем:
тогда имеем: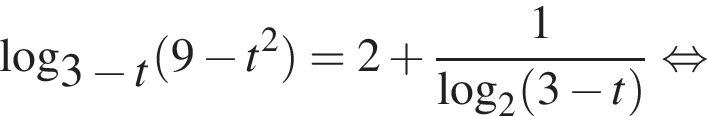

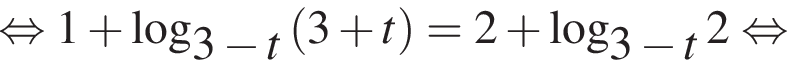


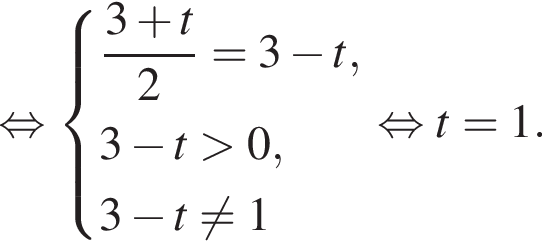

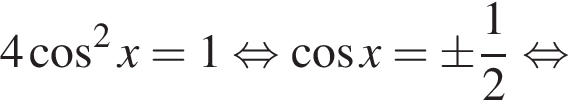


 б)
б) 













 б)
б) 






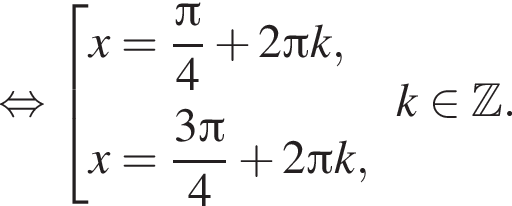
 с помощью тригонометрической окружности (см. рис.). Получим числа
с помощью тригонометрической окружности (см. рис.). Получим числа 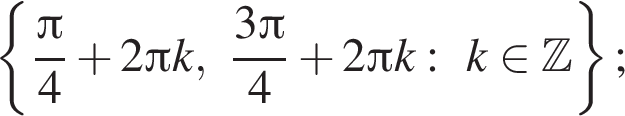 б)
б) 



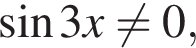 то есть
то есть 


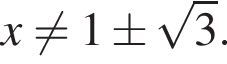 При этих условиях применим к правой части формулу
При этих условиях применим к правой части формулу  и получим равносильное уравнение
и получим равносильное уравнение



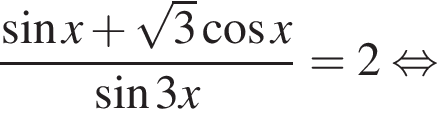


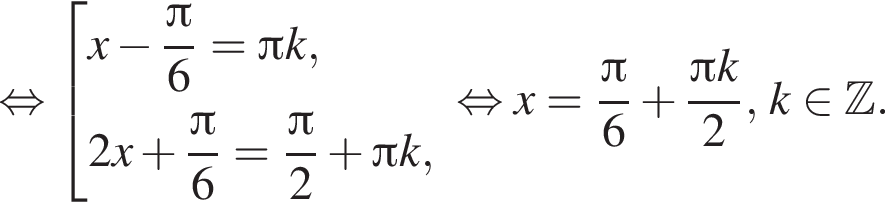







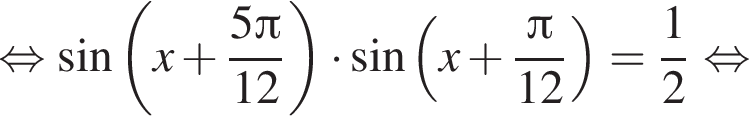





 или
или  то аргументы обоих логарифмов в исходном уравнении положительны. Следовательно, эти серии дают решения уравнения для всех целых k. Если
то аргументы обоих логарифмов в исходном уравнении положительны. Следовательно, эти серии дают решения уравнения для всех целых k. Если  или
или  то логарифмы не определены.
то логарифмы не определены. при помощи единичной окружности (см. рис.). Получим числа
при помощи единичной окружности (см. рис.). Получим числа 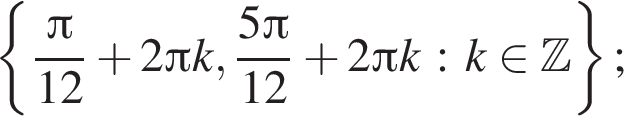 б)
б) 



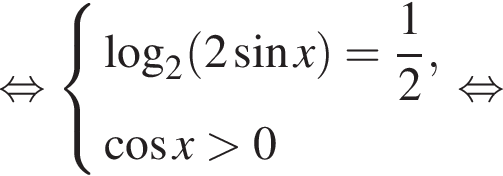
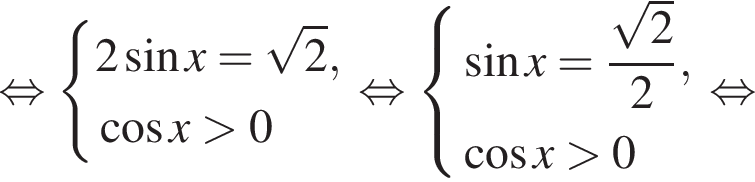



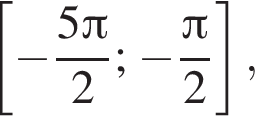 при помощи единичной тригонометрической окружности. Получаем число
при помощи единичной тригонометрической окружности. Получаем число  б)
б) 


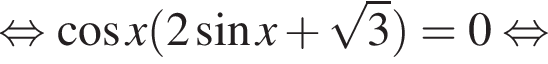

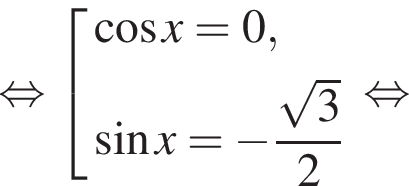


 б)
б) 

 получим:
получим:








 найдем при помощи тригонометрической окружности. Получим
найдем при помощи тригонометрической окружности. Получим  б)
б) 


 (⁎). Имеем:
(⁎). Имеем: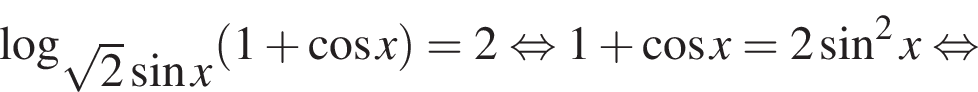





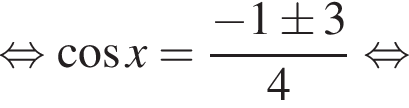


 равна π, поэтому из найденной серии решений в отрезок может попасть не более одного корня. Следовательно, число
равна π, поэтому из найденной серии решений в отрезок может попасть не более одного корня. Следовательно, число  б)
б) 










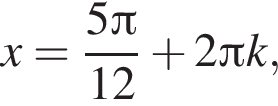
 б)
б) 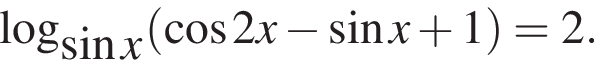

 При этом условии исходное уравнение равносильно следующим:
При этом условии исходное уравнение равносильно следующим:
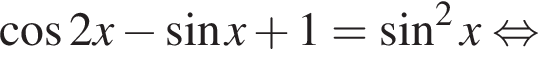






 б)
б) 


 При таких условиях числитель должен быть равен нулю:
При таких условиях числитель должен быть равен нулю:




 б)
б) 
 положительно и отлично от единицы при условиях
положительно и отлично от единицы при условиях 
 При этих условиях уравнение эквивалентно следующим:
При этих условиях уравнение эквивалентно следующим:








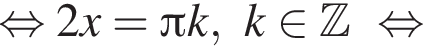
 и
и  получим
получим  что не удовлетворяет условию. При
что не удовлетворяет условию. При  получим
получим  что также не удовлетворяет условию. Следовательно, условию эквивалентности удовлетворяет только
что также не удовлетворяет условию. Следовательно, условию эквивалентности удовлетворяет только 





 б)
б) 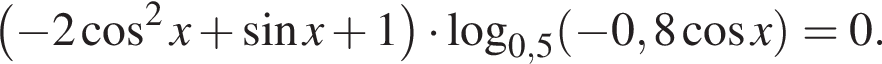

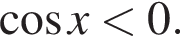 При этом условии уравнение эквивалентно совокупности:
При этом условии уравнение эквивалентно совокупности:

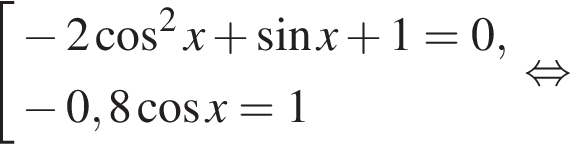


 при помощи двойного неравенства:
при помощи двойного неравенства:
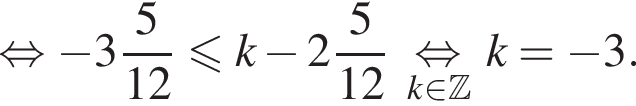



 б)
б) 





 Последнее условие означает, что
Последнее условие означает, что 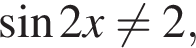 оно выполнено при всех значениях переменной. Условие
оно выполнено при всех значениях переменной. Условие  эквивалентно условию
эквивалентно условию  что верно, если одновременно
что верно, если одновременно  и
и 
 и
и  поэтому при переходе к основаниям
поэтому при переходе к основаниям 






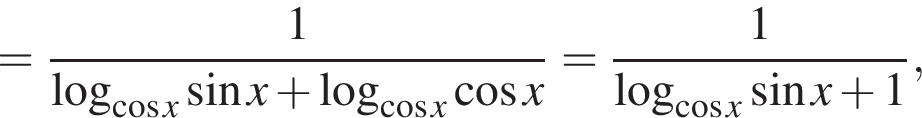





 тогда
тогда  а значит, левая часть уравнения записывается в виде
а значит, левая часть уравнения записывается в виде
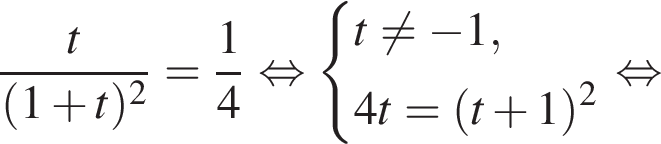




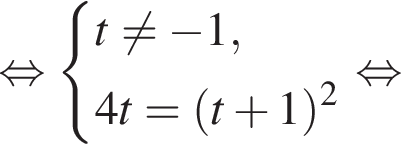





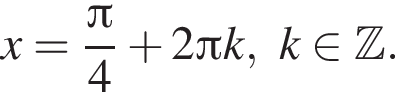


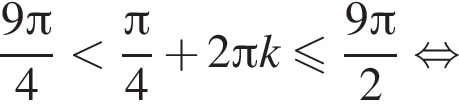



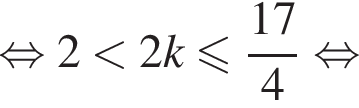
 б)
б) 


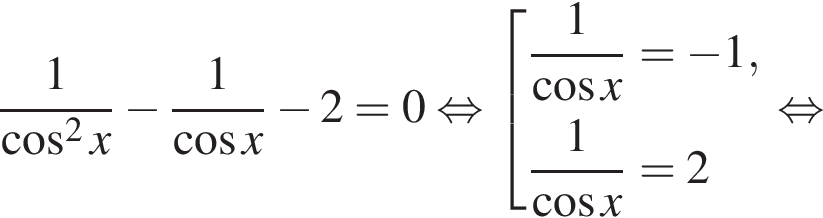






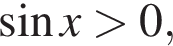

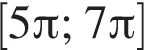 равна 2π. Расстояние между членами серии
равна 2π. Расстояние между членами серии  также равно 2π, причем никакое из них не совпадает с концами отрезка. Следовательно, в отрезок попадает лишь одно число из найденной серии. Это число
также равно 2π, причем никакое из них не совпадает с концами отрезка. Следовательно, в отрезок попадает лишь одно число из найденной серии. Это число 
 б)
б) 














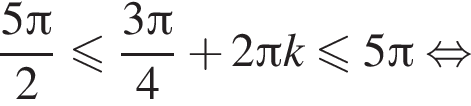
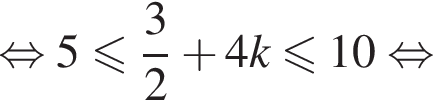










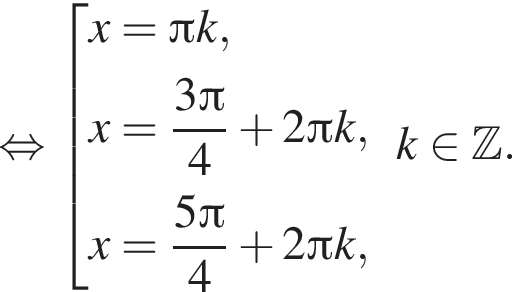


 при помощи тригонометрической окружности. Подходят: π,
при помощи тригонометрической окружности. Подходят: π,  б) π,
б) π, 







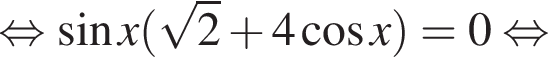





 б) π,
б) π,  2π.
2π.

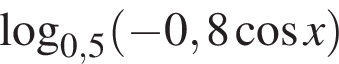 отличен от нуля. Следовательно, уравнение равносильно системе:
отличен от нуля. Следовательно, уравнение равносильно системе:



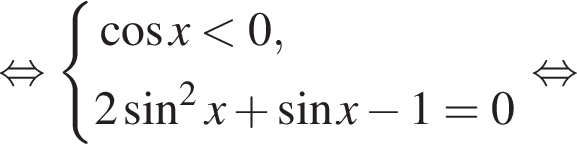
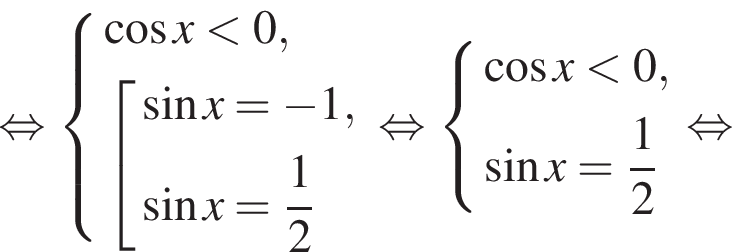



 отберем корни при помощи двойного неравенства:
отберем корни при помощи двойного неравенства: 









 Преобразуем его при этом условии:
Преобразуем его при этом условии:













 б)
б) 














 б)
б) 

 Преобразуем уравнение с учетом этого условия.
Преобразуем уравнение с учетом этого условия.



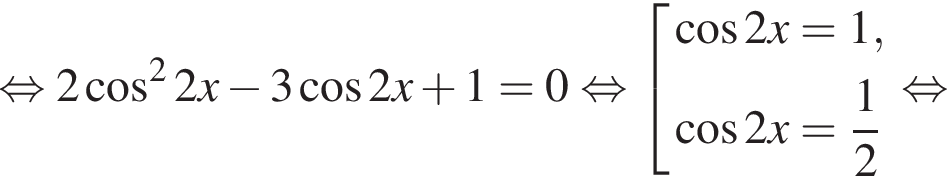


















 б)
б) 








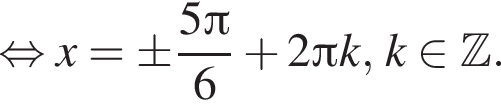
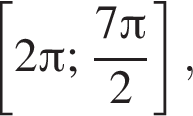 на тригонометрической окружности (см. рис.). Получаем:
на тригонометрической окружности (см. рис.). Получаем:  б)
б) 

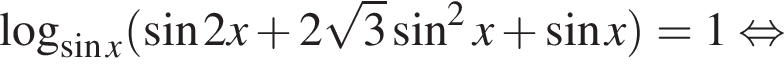

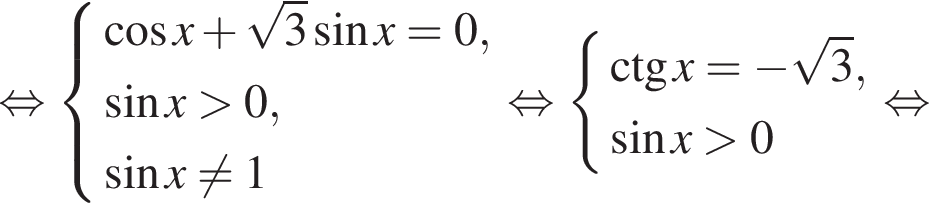

 длиной 1,5π попадает не более одного корня. Ясно, что этот корень равен
длиной 1,5π попадает не более одного корня. Ясно, что этот корень равен  б)
б) 

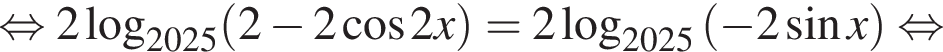




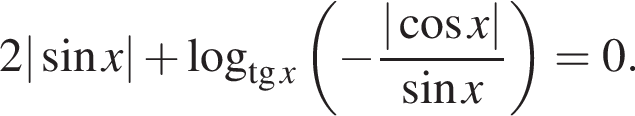
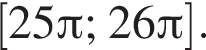
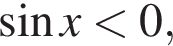 а
а  следовательно,
следовательно,  Тогда исходное уравнение примет вид:
Тогда исходное уравнение примет вид: