1. Тип 12 № 77419 

Источники:
Кодификатор ФИПИ/Решу ЕГЭ:
Наибольшее и наименьшее значение функций. Исследование степенных и иррациональных функций
i
Найдите точку максимума функции 
Решение. Найдем производную заданной функции:



Найдем нули производной:
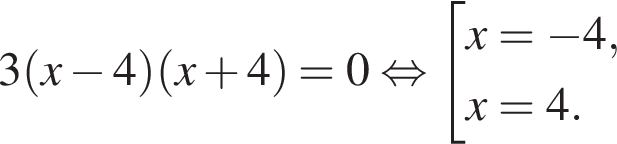
Определим знаки производной функции и изобразим на рисунке поведение функции:
Искомая точка максимума 
Ответ: −4.
Ответ: -4
77419
-4
 на отрезке
на отрезке 
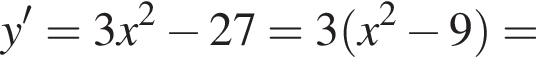



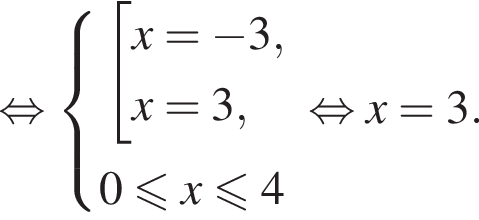
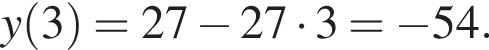
 на отрезке
на отрезке 
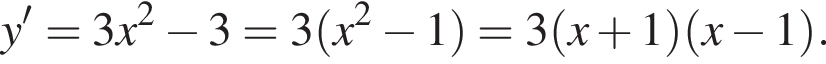



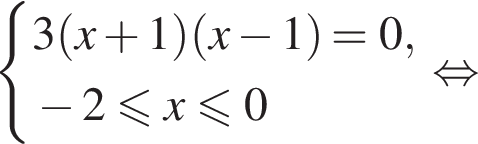

 заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение:
заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение: 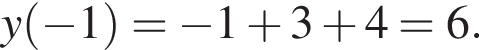





 на отрезке
на отрезке 

 на отрезке
на отрезке 

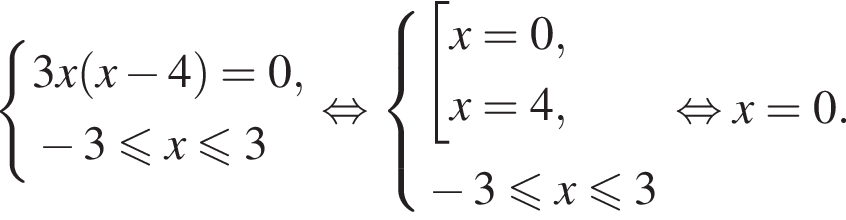










 на отрезке
на отрезке 

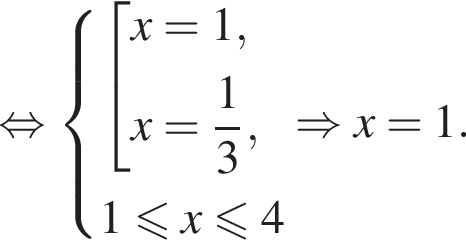

 на отрезке
на отрезке 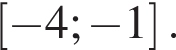
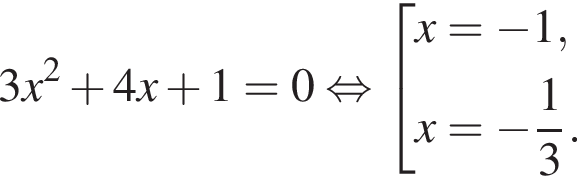
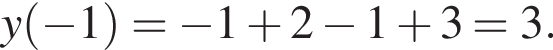






 на отрезке [0; 4].
на отрезке [0; 4].

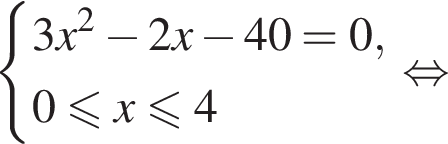


 на отрезке
на отрезке 
 найдем нули производной:
найдем нули производной: 


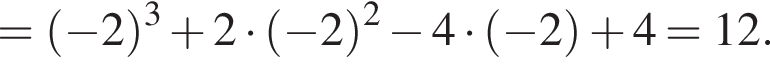







 на отрезке
на отрезке 

 заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение:
заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение: 








 на отрезке
на отрезке 






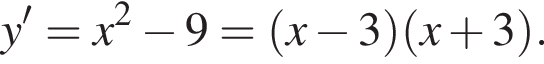





 на отрезке
на отрезке 








 на отрезке
на отрезке 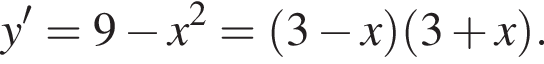






 на отрезке
на отрезке 




 на отрезке
на отрезке 





 на отрезке
на отрезке 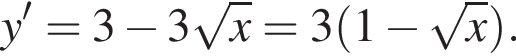



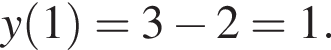



 на отрезке
на отрезке 



 на отрезке
на отрезке 

 и найдем ее производную:
и найдем ее производную: 
 на отрезке
на отрезке 


 на отрезке
на отрезке  и найдем производную этой функции:
и найдем производную этой функции: 




 на отрезке
на отрезке  и найдем производную этой функции:
и найдем производную этой функции: 
 на отрезке
на отрезке 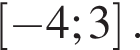

 найдем нули производной:
найдем нули производной: 
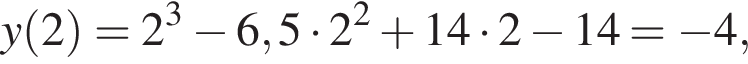


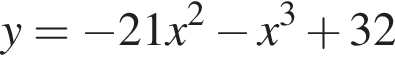 определена на множестве всех действительных чисел.
определена на множестве всех действительных чисел.


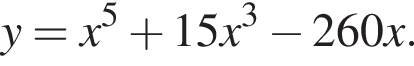





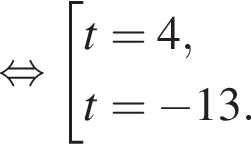
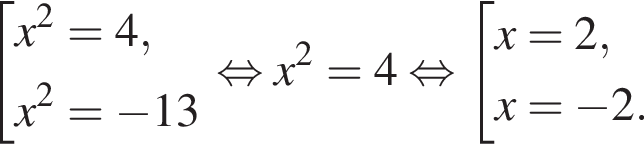
 на отрезке
на отрезке 

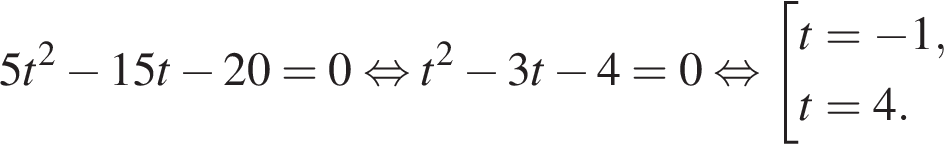














 на отрезке [−3; 3].
на отрезке [−3; 3].


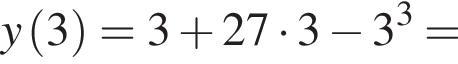



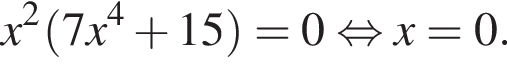

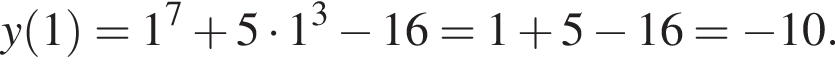




 Найдём её производную:
Найдём её производную: 







 Найдем нули производной:
Найдем нули производной:

 положительна, следовательно, функция возрастает на отрезке. Таким образом, наибольшее значение функция на данном отрезке принимает
положительна, следовательно, функция возрастает на отрезке. Таким образом, наибольшее значение функция на данном отрезке принимает 













