
Окружность с центром O, расположенном внутри прямоугольной трапеции ABCD, проходит через вершины B и C большей боковой стороны этой трапеции и касается боковой стороны AD в точке T.
а) Докажите, что угол BOC вдвое больше угла BTC.
б) Найдите расстояние от точки T до прямой BC, если основания трапеции AB и CD равны 4 и 9 соответственно.
Решение. а) Угол BTC вписан в окружность, а угол BOC — соответствующий ему центральный угол. Следовательно, ∠BOC = 2∠BTC.
б) Из условия касания окружности и стороны AD следует, что прямые OT и AD перпендикулярны. Пусть окружность вторично пересекает прямую AB в точке L и сторону CD — в точке M. Тогда диаметр окружности, перпендикулярный стороне AB, делит каждую из хорд BL и CM пополам. Обозначим OT = r, тогда
По теореме Пифагора  По теореме о касательной и секущей
По теореме о касательной и секущей  Следовательно,
Следовательно, 
Аналогично 
Из теоремы синусов следует, что BC = 2r · sin ∠BTC. Пусть h — искомое
расстояние от точки T до прямой BC . Выразим площадь треугольника BTC двумя способами:
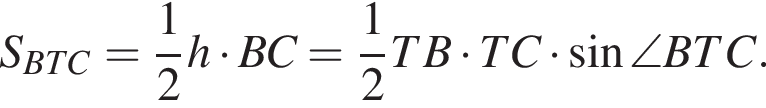
Отсюда получаем, что  Следовательно,
Следовательно, 
Ответ: 6.
Примечание.
Заметим, что AL больше радиуса окружности, а DC меньше диаметра, поэтому DC < 2AL. В данной задаче АВ = 4, CD = 9, поэтому точка В лежит на отрезке AL. При других числовых данных точка В может лежать на продолжении отрезка АL за точку L. Приведенное решение остается верным и для такого случая.
Приведем решение пункта б) Сергей Николаева.
Пусть K — точка пересечения прямых AD и ВC, точка S — основание перпендикуляра, опущенного из точки T на прямую BC. Треугольники DKC и AKB подобны по двум углам, поэтому 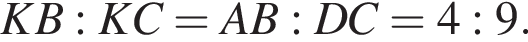 По теореме об отрезках секущей
По теореме об отрезках секущей  тогда
тогда  и
и  Треугольники KTS и KCD подобны по двум углам, поэтому
Треугольники KTS и KCD подобны по двум углам, поэтому  откуда
откуда 
Еще один способ решения
приведен нами на сайте Решу ОГЭ в задании 340855.
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) ИЛИ имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) ИЛИ при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | 1 |
| Решение не соответствует ни одному из критериев, приведённых выше | 0 |
| Максимальный балл | 3 |
 и LM = 1.
и LM = 1. Значит, прямые OH и MN параллельны, а поскольку прямая OQ — средняя линия трапеции, то параллельны прямые OQ и KN. Противоположные стороны четырёхугольника NQOH попарно параллельны, следовательно, четырехугольник NQOH — параллелограмм.
Значит, прямые OH и MN параллельны, а поскольку прямая OQ — средняя линия трапеции, то параллельны прямые OQ и KN. Противоположные стороны четырёхугольника NQOH попарно параллельны, следовательно, четырехугольник NQOH — параллелограмм.





 Трапеция KLMN — равнобедренная, поэтому
Трапеция KLMN — равнобедренная, поэтому



 При этом
При этом  Следовательно,
Следовательно, 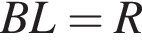 и
и  Таким образом,
Таким образом, 
 поскольку прямые BC и AQ параллельны. Углы
поскольку прямые BC и AQ параллельны. Углы  и
и 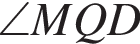 равны, поскольку оба равны половине дуги MP (первый — угол между касательной и хордой, второй — вписанный угол), откуда и следует утверждение задачи.
равны, поскольку оба равны половине дуги MP (первый — угол между касательной и хордой, второй — вписанный угол), откуда и следует утверждение задачи.
 откуда
откуда 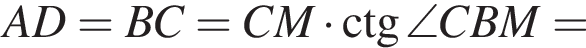


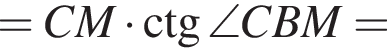




 то есть
то есть  Следовательно,
Следовательно,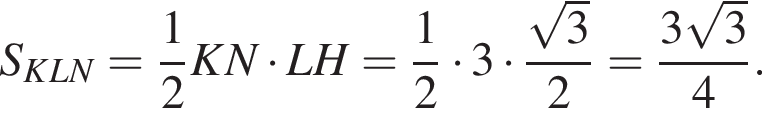
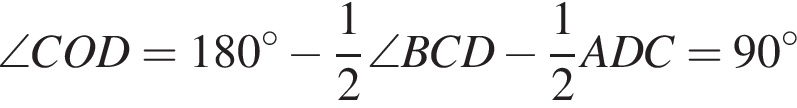
 Аналогично, углы CO1D и ODO1 — прямые. Значит, OCO1D — прямоугольник, поэтому CD = OO1.
Аналогично, углы CO1D и ODO1 — прямые. Значит, OCO1D — прямоугольник, поэтому CD = OO1.



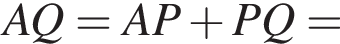











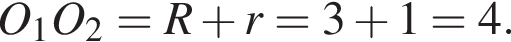

 Тогда
Тогда  Получаем:
Получаем:







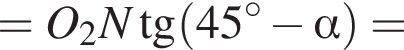

 Аналогично,
Аналогично, 








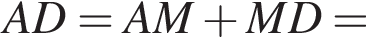








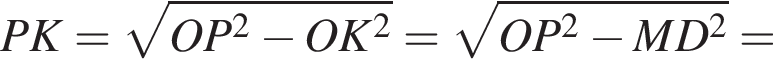



 Тогда
Тогда 

 и
и  откуда
откуда


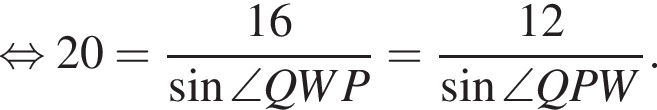



 откуда, учитывая, что угол W острый, находим, что
откуда, учитывая, что угол W острый, находим, что  и, значит,
и, значит, 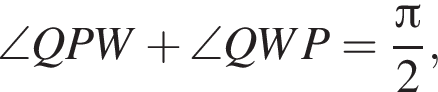 то есть
то есть  треугольник PQW прямоугольный.
треугольник PQW прямоугольный. Отсюда следует, что PQ и AC параллельны и
Отсюда следует, что PQ и AC параллельны и  Аналогично треугольники CQW и CBD подобны с коэффициентом подобия
Аналогично треугольники CQW и CBD подобны с коэффициентом подобия  следовательно, QW и BD параллельны и BD = 28. Угол между прямыми AC и BD равен углу между прямыми PQ и QW. Угол между диагоналями четырёхугольника ABCD прямой. Поэтому его площадь равна
следовательно, QW и BD параллельны и BD = 28. Угол между прямыми AC и BD равен углу между прямыми PQ и QW. Угол между диагоналями четырёхугольника ABCD прямой. Поэтому его площадь равна 
 углы CAD и MDA равны. Углы CAD и BAM равны половине дуги AM, поэтому они равны между собой, что и требовалось доказать.
углы CAD и MDA равны. Углы CAD и BAM равны половине дуги AM, поэтому они равны между собой, что и требовалось доказать. откуда
откуда  а
а  Треугольники AOD и COB подобны, поэтому
Треугольники AOD и COB подобны, поэтому  тогда
тогда 


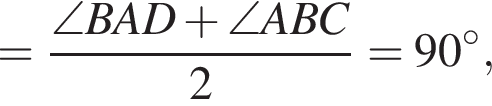
 Следовательно, КО1 — медиана, проведенная к гипотенузе АВ прямоугольного треугольника АО1В.
Следовательно, КО1 — медиана, проведенная к гипотенузе АВ прямоугольного треугольника АО1В.


 Значит, хорды окружности AE и AK стягивают равные дуги. Поэтому эти хорды равны.
Значит, хорды окружности AE и AK стягивают равные дуги. Поэтому эти хорды равны. , поэтому DE = AB = DC.
, поэтому DE = AB = DC.

 откуда
откуда 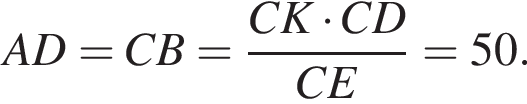
 UW — высота трапеции, а точка V — середина отрезка KL. Значит,
UW — высота трапеции, а точка V — середина отрезка KL. Значит,
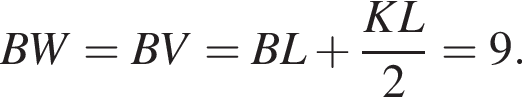




 UW — высота трапеции, а точка V — середина отрезка KL. Тогда
UW — высота трапеции, а точка V — середина отрезка KL. Тогда 












 как противоположные углы в параллелограмме. Они также являются вписанными углами, поэтому и дуги BE и BK равны. Следовательно, хорды BK и BE равны, поскольку они стягивают равные дуги.
как противоположные углы в параллелограмме. Они также являются вписанными углами, поэтому и дуги BE и BK равны. Следовательно, хорды BK и BE равны, поскольку они стягивают равные дуги. как односторонние углы при параллельных прямых. Следовательно, дуги BK и BE равны
как односторонние углы при параллельных прямых. Следовательно, дуги BK и BE равны  Тогда дуга KE равна
Тогда дуга KE равна  Поэтому вписанный
Поэтому вписанный  Тогда по теореме синусов для треугольников ABC и BKE
Тогда по теореме синусов для треугольников ABC и BKE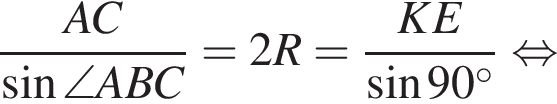



 а поскольку
а поскольку  как угол между касательной и хордой, треугольник KLN равнобедренный с основанием KN.
как угол между касательной и хордой, треугольник KLN равнобедренный с основанием KN.
 Угол MPQ смежный с углом BPQ, поэтому
Угол MPQ смежный с углом BPQ, поэтому  Отрезок MN — средняя линия трапеции ABCD, она параллельна BC, поэтому
Отрезок MN — средняя линия трапеции ABCD, она параллельна BC, поэтому 
 а значит, он вписанный.
а значит, он вписанный.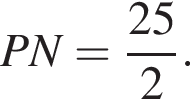 Средняя линия трапеции равна полусумме оснований:
Средняя линия трапеции равна полусумме оснований:  Через вершину трапеции B проведем прямую, параллельную боковой стороне CD, пусть L — точка ее пересечения с основанием AD. Стороны треугольника ABL равны 26, 17 и 25. Найдем его площадь по формуле Герона, затем найдем высоту h, проведенную к стороне AL, она будет являться также высотой трапеции ABCD:
Через вершину трапеции B проведем прямую, параллельную боковой стороне CD, пусть L — точка ее пересечения с основанием AD. Стороны треугольника ABL равны 26, 17 и 25. Найдем его площадь по формуле Герона, затем найдем высоту h, проведенную к стороне AL, она будет являться также высотой трапеции ABCD:


 по теореме синусов для треугольника MPN найдем радиус окружности, описанной около треугольника MPQ:
по теореме синусов для треугольника MPN найдем радиус окружности, описанной около треугольника MPQ: 
 поэтому можно найти MQ по теореме синусов для треугольника MQN:
поэтому можно найти MQ по теореме синусов для треугольника MQN: 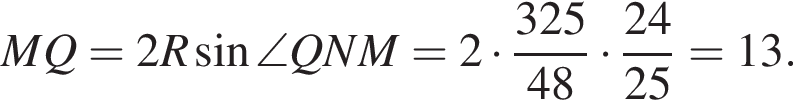

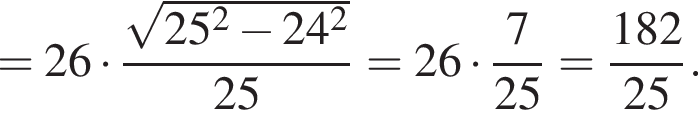




 Тогда
Тогда  откуда
откуда  и
и  откуда
откуда 
 откуда
откуда 
 В треугольнике MPN угол M равен углу А, тогда по теореме косинусов имеем:
В треугольнике MPN угол M равен углу А, тогда по теореме косинусов имеем: 

 откуда
откуда  или
или 



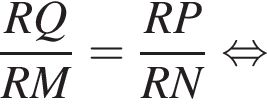









 Средняя линия трапеции ABCD равна полусумме оснований:
Средняя линия трапеции ABCD равна полусумме оснований:  Следовательно, треугольник MQN равнобедренный. Тогда
Следовательно, треугольник MQN равнобедренный. Тогда 
 откуда
откуда



 Отрезок MN — средняя линия трапеции ABCD, она параллельна основанию BC, а тогда
Отрезок MN — средняя линия трапеции ABCD, она параллельна основанию BC, а тогда  как односторонние углы при параллельных прямых. Следовательно,
как односторонние углы при параллельных прямых. Следовательно,  Для смежных углов справедливо равенство
Для смежных углов справедливо равенство  а значит,
а значит,  В четырёхугольнике MPQN сумма противоположных углов равна 180°, поэтому вокруг него можно описать окружность. Таким образом, точки M, N, P и Q лежат на одной окружности, что и требовалось доказать.
В четырёхугольнике MPQN сумма противоположных углов равна 180°, поэтому вокруг него можно описать окружность. Таким образом, точки M, N, P и Q лежат на одной окружности, что и требовалось доказать.  (эти углы равны как соответственные углы при параллельных прямых). В пункте а) было показано, что
(эти углы равны как соответственные углы при параллельных прямых). В пункте а) было показано, что  это означает, что
это означает, что  и, следовательно, точки A, D, P и Q тоже лежат на одной окружности.
и, следовательно, точки A, D, P и Q тоже лежат на одной окружности.  и
и  Значит, треугольники DPC и AQB подобны по двум углам. Следовательно,
Значит, треугольники DPC и AQB подобны по двум углам. Следовательно,  поскольку по условию AQ и BQ перпендикулярны.
поскольку по условию AQ и BQ перпендикулярны. 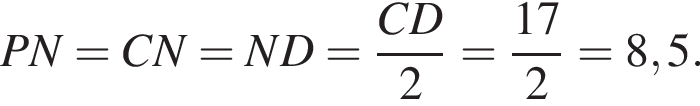 С другой стороны, средняя линия трапеции
С другой стороны, средняя линия трапеции 
 тогда
тогда 
 Заметим, что
Заметим, что  следовательно, по теореме обратной теореме Пифагора треугольник ABE прямоугольный, с прямым углом BAE. Значит, треугольник PNM также прямоугольный. Применяя теорему Пифагора, получаем:
следовательно, по теореме обратной теореме Пифагора треугольник ABE прямоугольный, с прямым углом BAE. Значит, треугольник PNM также прямоугольный. Применяя теорему Пифагора, получаем:



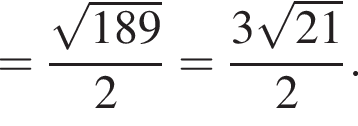


 а радиус описанной окружности равен 18.
а радиус описанной окружности равен 18.

 Заметим, что
Заметим, что 
 как вписанные углы, опирающиеся на одну дугу. Аналогично
как вписанные углы, опирающиеся на одну дугу. Аналогично  Тогда
Тогда  Но
Но  следовательно, треугольник AOP — равнобедренный, а тогда
следовательно, треугольник AOP — равнобедренный, а тогда 

 как хорды, стягивающие равные дуги. Следовательно, треугольник APC равносторонний. Искомое расстояние d равно его высоте:
как хорды, стягивающие равные дуги. Следовательно, треугольник APC равносторонний. Искомое расстояние d равно его высоте: 


 cледовательно, вокруг четырехугольника ABCD можно описать окружность.
cледовательно, вокруг четырехугольника ABCD можно описать окружность.
 тогда:
тогда: 


 тогда
тогда  при
при 



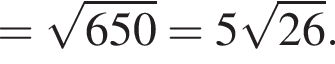




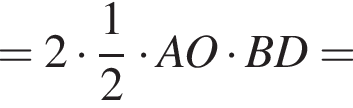

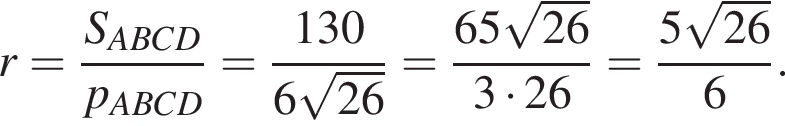
 и не имеет корней. Следовательно, такая конфигураций невозможна.
и не имеет корней. Следовательно, такая конфигураций невозможна.
 а AB = 6, расположены две окружности. Окружность с центром в точке K, радиус которой равен 2, касается сторон AB и AD. Окружность с центром в точке L, радиус которой равен 1, касается стороны CD и первой окружности.
а AB = 6, расположены две окружности. Окружность с центром в точке K, радиус которой равен 2, касается сторон AB и AD. Окружность с центром в точке L, радиус которой равен 1, касается стороны CD и первой окружности.


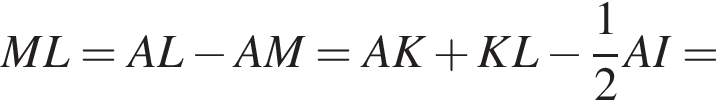





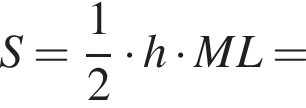




 Отсюда CG = 4. Заметим теперь, что EF — средняя линия треугольника ACG, значит,
Отсюда CG = 4. Заметим теперь, что EF — средняя линия треугольника ACG, значит,  Что и требовалось доказать.
Что и требовалось доказать.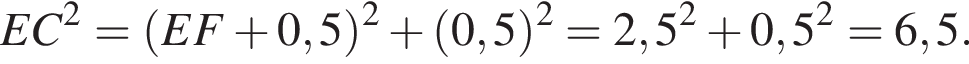


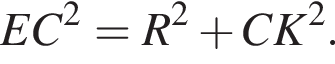 Отсюда
Отсюда 






 тогда из вписанности четырехугольника ABCD следует, что
тогда из вписанности четырехугольника ABCD следует, что  а значит,
а значит,  и
и  Пусть теперь
Пусть теперь 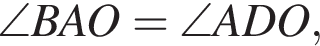 тогда
тогда  откуда
откуда  и
и  В любом случае
В любом случае  следовательно, в четырехугольник АBCD можно вписать окружность.
следовательно, в четырехугольник АBCD можно вписать окружность.  тогда
тогда 
 следовательно, в треугольнике ABC высота BO больше гипотенузы, что невозможно. Таким образом,
следовательно, в треугольнике ABC высота BO больше гипотенузы, что невозможно. Таким образом,  откуда
откуда  и
и 
 из чего следует, что
из чего следует, что  и
и  тогда
тогда 

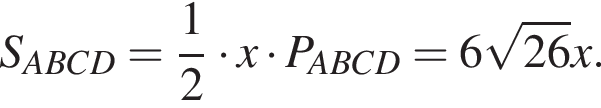
 следовательно,
следовательно, 



 тогда
тогда 

 то есть
то есть  Следовательно,
Следовательно, 






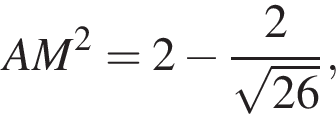 следовательно,
следовательно,  Таким образом,
Таким образом,  поэтому отрезок CM также найдем из теореме косинусов:
поэтому отрезок CM также найдем из теореме косинусов:






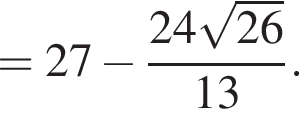


 где R — радиус окружности. Значит,
где R — радиус окружности. Значит, 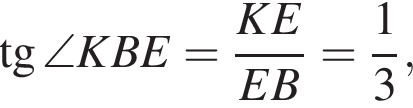 откуда
откуда












 то
то  но тогда трапеция
но тогда трапеция  а тогда
а тогда 
 откуда
откуда  Пусть для определенности
Пусть для определенности  и
и  Тогда:
Тогда: 

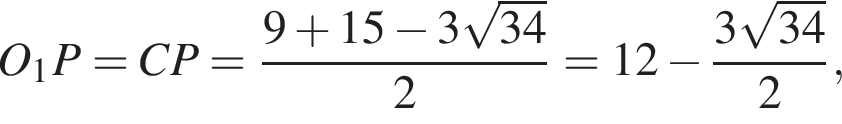






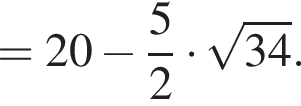








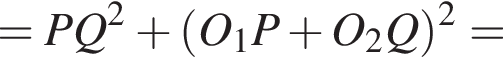



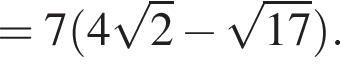

 и
и  Тогда точка M — точка пересечения высот треугольника ACD. Cледовательно, точка M лежит на прямой BD.
Тогда точка M — точка пересечения высот треугольника ACD. Cледовательно, точка M лежит на прямой BD.

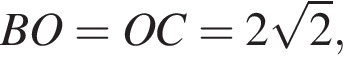








 Заметим, что
Заметим, что  Тогда по теореме косинусов имеем:
Тогда по теореме косинусов имеем:

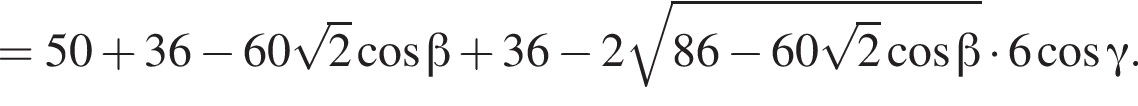








 откуда угол CMN прямой, значит, точки C, A, N лежат на одной прямой и угол BAK равен 45°, либо
откуда угол CMN прямой, значит, точки C, A, N лежат на одной прямой и угол BAK равен 45°, либо  откуда
откуда


 и
и  что противоречит условию.
что противоречит условию.


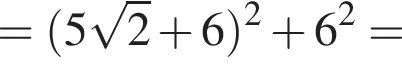





 Из этого следует, что прямоугольные треугольники CBK и CHP подобны по двум углам.
Из этого следует, что прямоугольные треугольники CBK и CHP подобны по двум углам.








 то есть
то есть 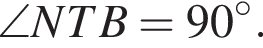 Аналогично
Аналогично  Тогда отрезки BT, CP и NF — высоты треугольника NBC, которые пересекаются в точке H. По свойству вписанных углов
Тогда отрезки BT, CP и NF — высоты треугольника NBC, которые пересекаются в точке H. По свойству вписанных углов


 а поскольку четырехугольник APFC вписанный, то
а поскольку четырехугольник APFC вписанный, то



 и
и


 Заметим, что треугольники APF и ATF равны по стороне AF и двум углам. Значит, PF = TF, и, следовательно,
Заметим, что треугольники APF и ATF равны по стороне AF и двум углам. Значит, PF = TF, и, следовательно,


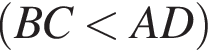 окружности, вписанные в треугольники АВС и ACD, делят диагональ АС в отношении 2 : 1 : 1, считая от точки А.
окружности, вписанные в треугольники АВС и ACD, делят диагональ АС в отношении 2 : 1 : 1, считая от точки А.

 Тогда
Тогда
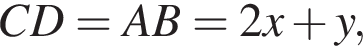

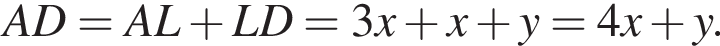
 Заметим, что
Заметим, что









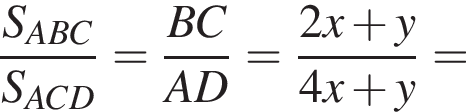
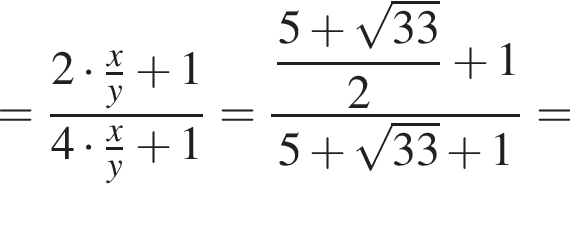
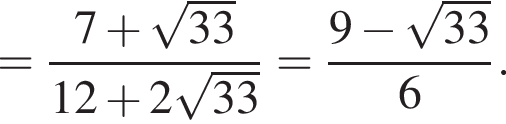

 Следовательно, отрезок TP перпендикулярен диагонали AC. Четырехугольник TPCD — описанный, поэтому ##
Следовательно, отрезок TP перпендикулярен диагонали AC. Четырехугольник TPCD — описанный, поэтому ##




 Прибавив к этому равенству равенство (1), получим
Прибавив к этому равенству равенство (1), получим  и
и  Из условия
Из условия  значит, из подобия треугольников APK и CPD по трем углам следует, что
значит, из подобия треугольников APK и CPD по трем углам следует, что  Пусть
Пусть 
 Тогда по теореме Пифагора в треугольнике ACD
Тогда по теореме Пифагора в треугольнике ACD  Треугольники APT и ADC подобны по трем углам, следовательноm
Треугольники APT и ADC подобны по трем углам, следовательноm

 Заметим, что окружность, вписанная в четырехугольник TPCD, вписана и в треугольник ACD. Площадь треугольника равна произведению радиуса вписанной в него окружности и его полупериметра, откуда
Заметим, что окружность, вписанная в четырехугольник TPCD, вписана и в треугольник ACD. Площадь треугольника равна произведению радиуса вписанной в него окружности и его полупериметра, откуда