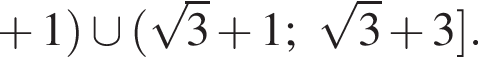1. Тип Д13 C3 № 505690 

Классификатор алгебры: Системы неравенств
Методы алгебры: Введение замены
Кодификатор ФИПИ/Решу ЕГЭ:
Системы сложных неравенств. Системы, содержащие логарифмическое неравенство
i
Решите систему неравенств 
Решение. Решим первое неравенство системы:


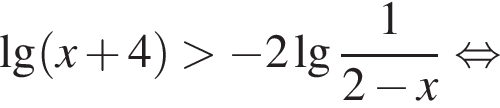











Решения первого неравенств системы представляются множеством 
Решим второе неравенство системы на  Пусть
Пусть  Тогда
Тогда






Таким образом, 
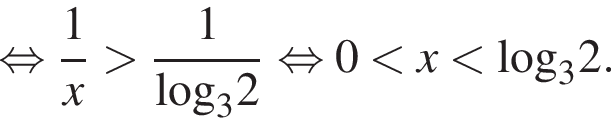
Ответ: 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ. | 3 |
| Обоснованно получены верные ответы в обоих неравенствах исходной системы. | 2 |
| Обоснованно получен верный ответ в одном неравенстве исходной системы. ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения системы неравенств. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 3 |
Ответ: 

505690

Классификатор алгебры: Системы неравенств
Методы алгебры: Введение замены







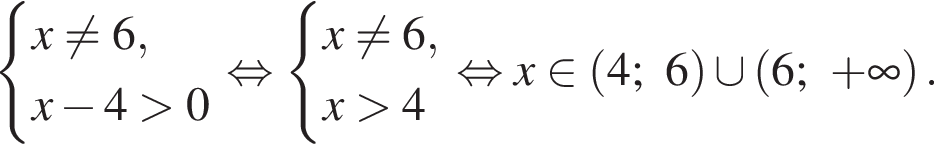





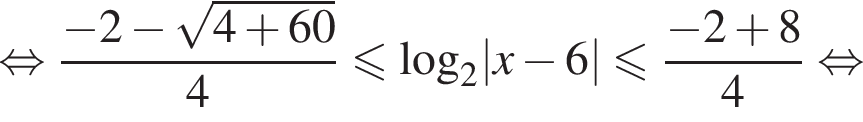








 Ясно, что
Ясно, что  Теперь получим и решения исходной системы:
Теперь получим и решения исходной системы: 

 Для таких
Для таких 
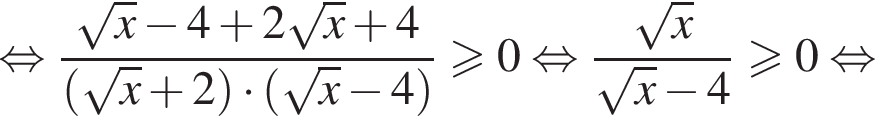

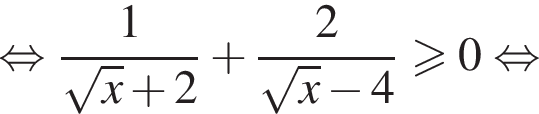
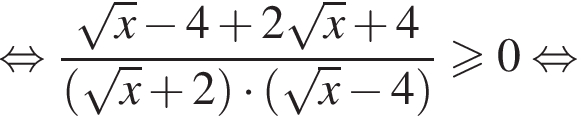



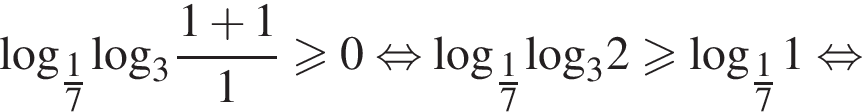







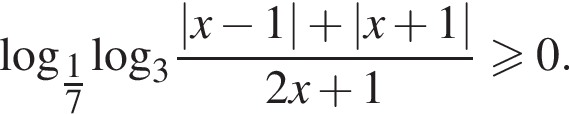





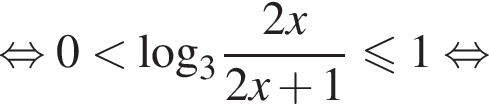




 при
при  невыполнимо. Следовательно, решения исходной системы
невыполнимо. Следовательно, решения исходной системы 
 Для таких значений переменной будем иметь:
Для таких значений переменной будем иметь:





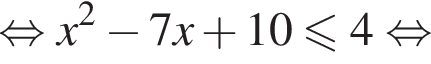

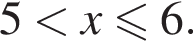



 В таком случае первое неравенство системы будет иметь вид:
В таком случае первое неравенство системы будет иметь вид: 




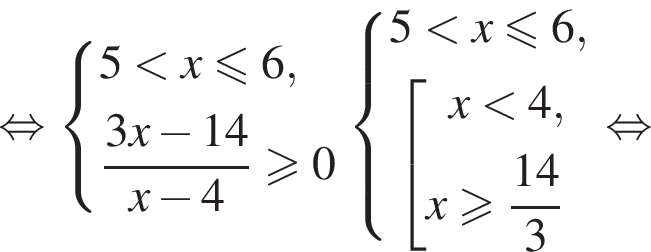






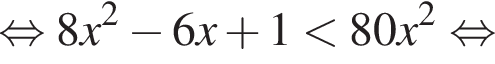

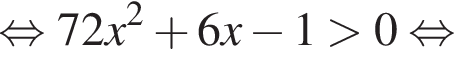




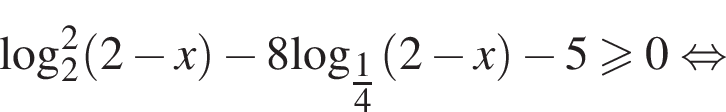



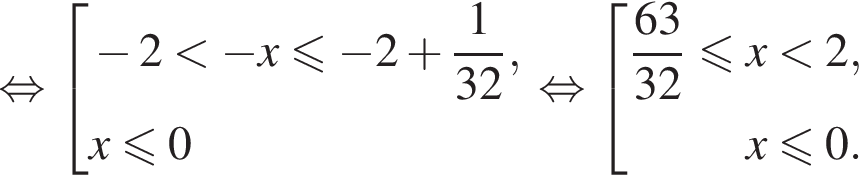

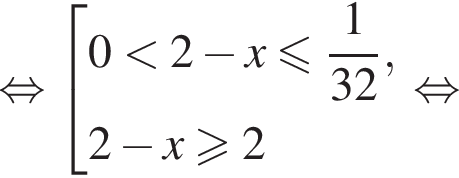


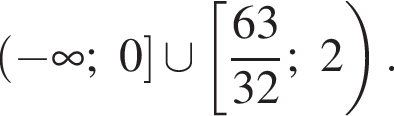


 Для таких
Для таких 
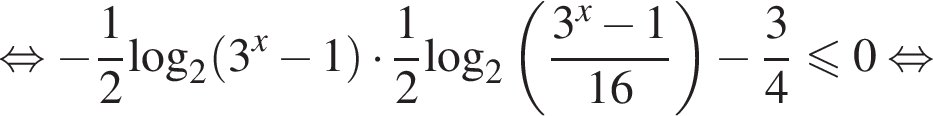



 Тогда:
Тогда:








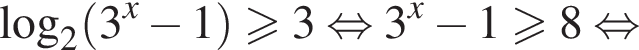




 выражение
выражение  смысла не имеет, поскольку при этих значениях x
смысла не имеет, поскольку при этих значениях x 



 Таким образом, ни одно решение первого неравенства не является также решением второго неравенства.
Таким образом, ни одно решение первого неравенства не является также решением второго неравенства.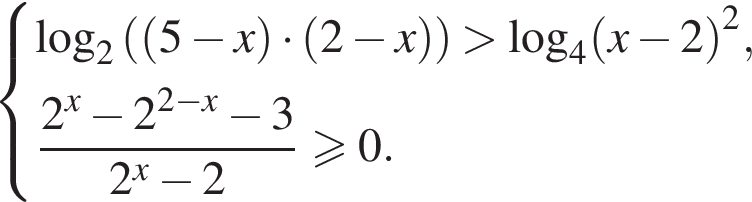








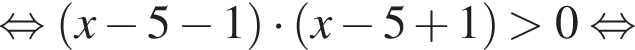
















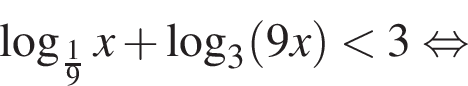




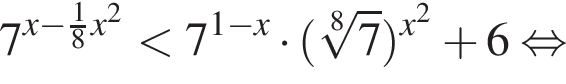

 Тогда:
Тогда: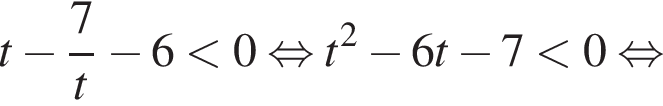









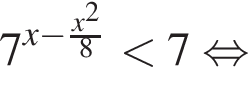


 и
и 
 (неравенство очевидное).
(неравенство очевидное). (неравенство очевидное).
(неравенство очевидное).
















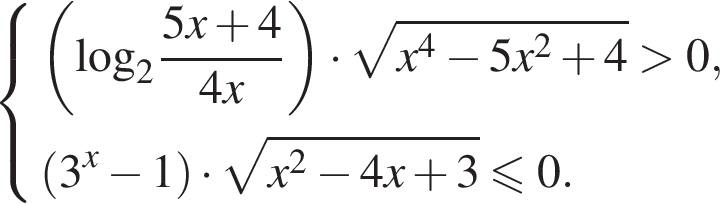


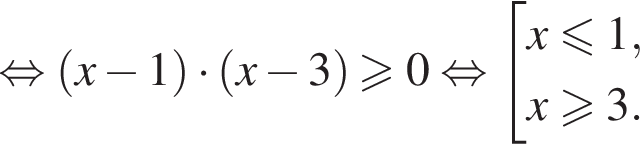


 только при
только при  Далее будем решать неравенство
Далее будем решать неравенство 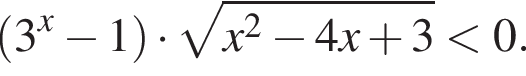 Поскольку при
Поскольку при  то на этом множестве неравенство
то на этом множестве неравенство  равносильно неравенству
равносильно неравенству  откуда получим
откуда получим 







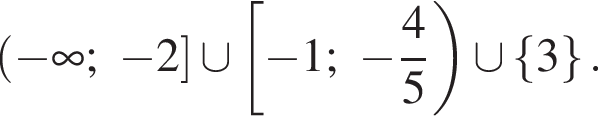 На этом множестве исходное первое неравенство будет равносильным неравенствам:
На этом множестве исходное первое неравенство будет равносильным неравенствам: 





















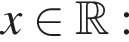










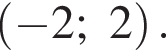


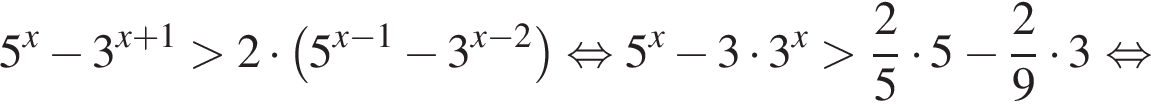
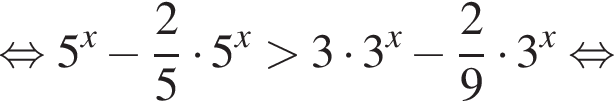















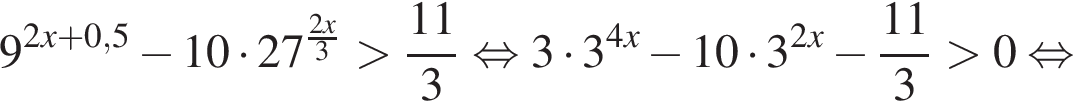



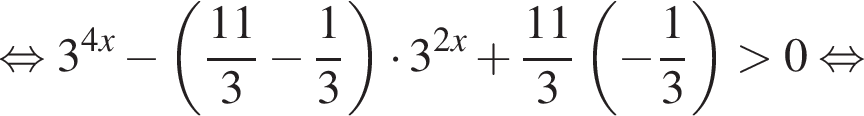
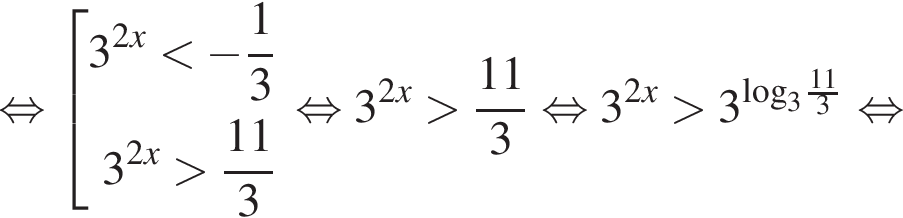
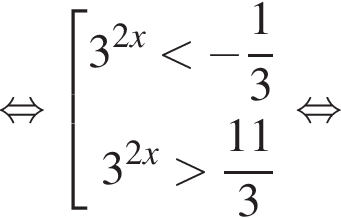



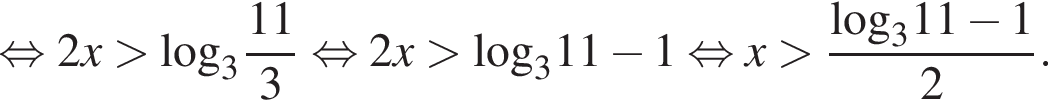


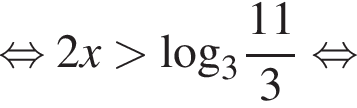









 Тогда:
Тогда: 
 А это значит:
А это значит:



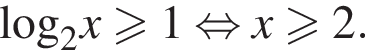










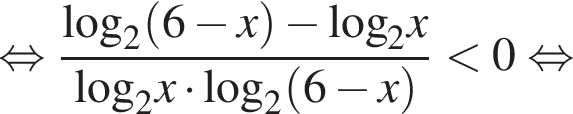





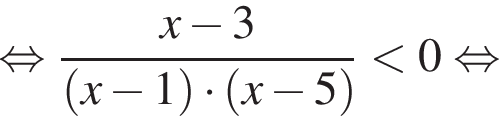






 Тогда:
Тогда:








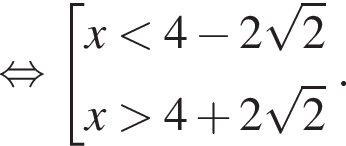
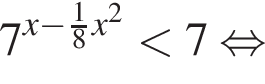



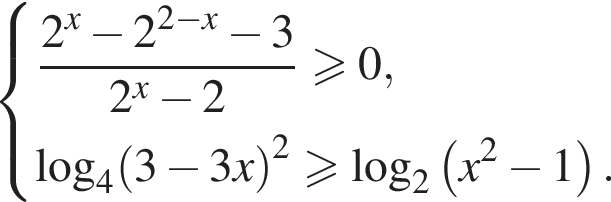




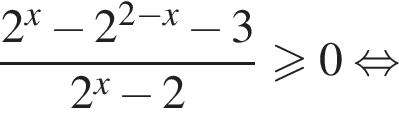
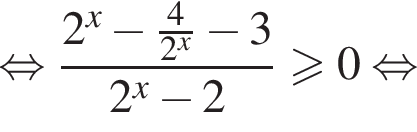
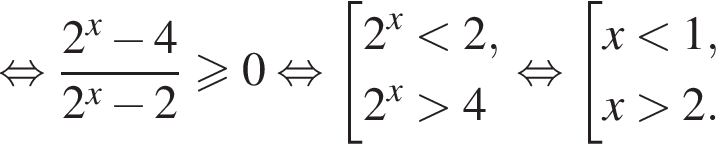





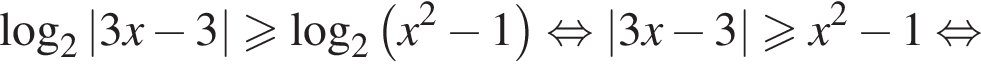








 или
или 



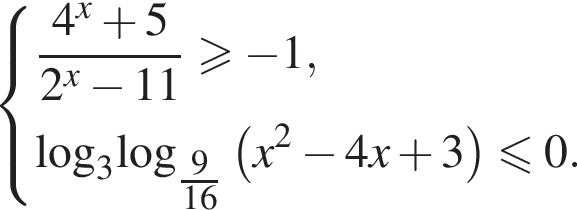











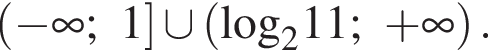

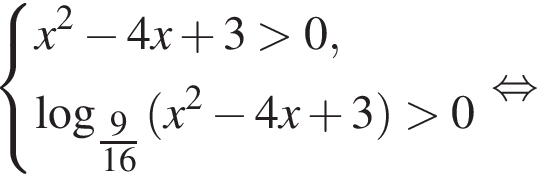



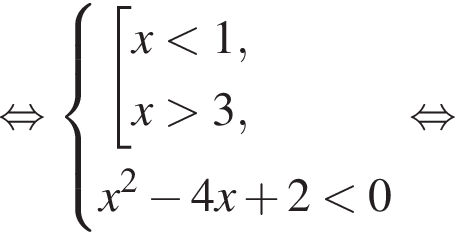


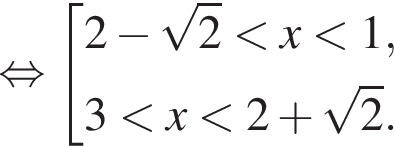











 и
и  Действительно,
Действительно, 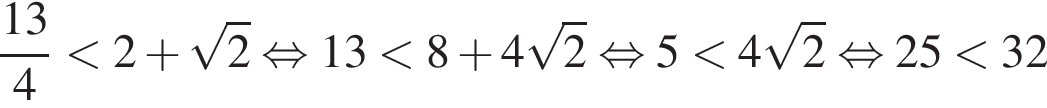



 и
и  Докажем, что
Докажем, что 

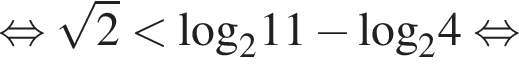






 получим:
получим:  (неравенство истинно). Итак,
(неравенство истинно). Итак, 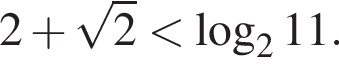
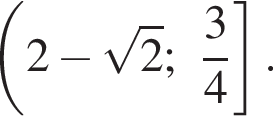



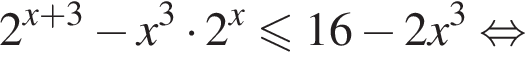
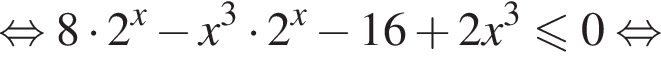
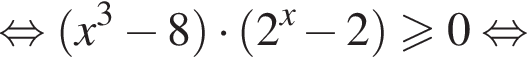
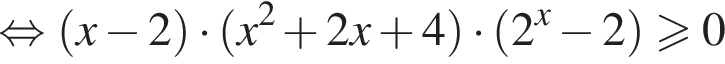



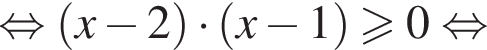
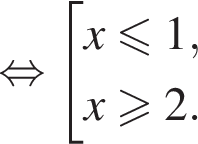








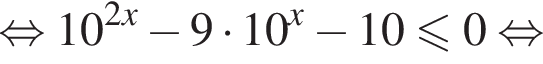


 Следовательно, решением второго неравенства системы является множество
Следовательно, решением второго неравенства системы является множество 








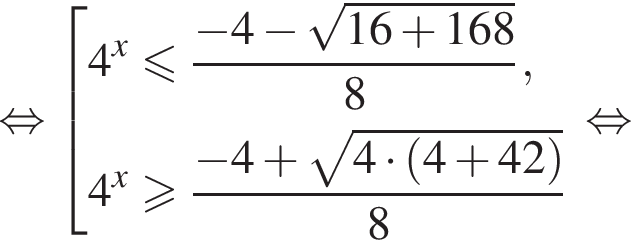




 решений не имеет.
решений не имеет.
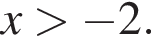 Для таких
Для таких 



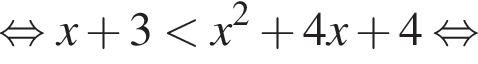



 и
и 

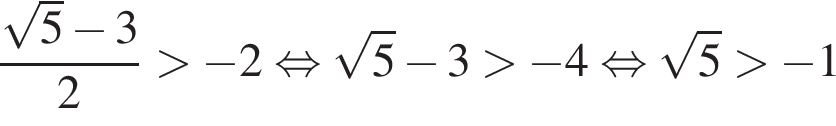



 Неравенство
Неравенство  очевидно, поскольку
очевидно, поскольку 






 (неравенство очевидное).
(неравенство очевидное).







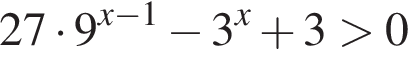 при всех
при всех 




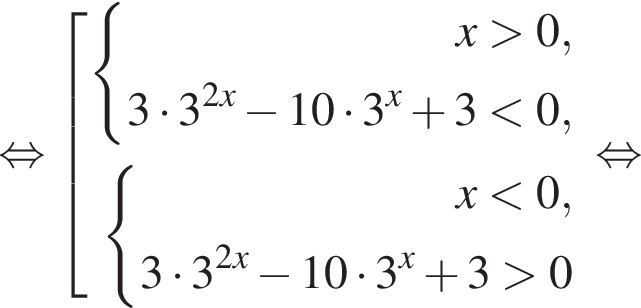

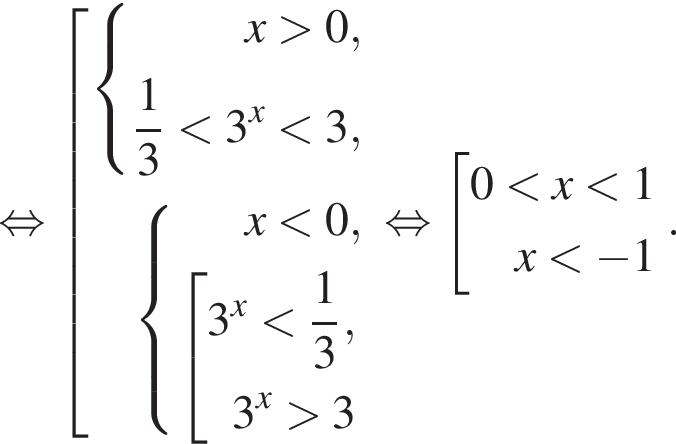


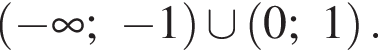





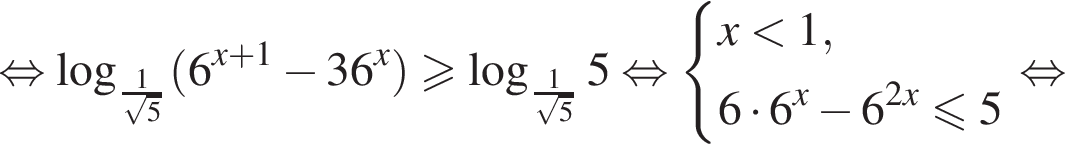







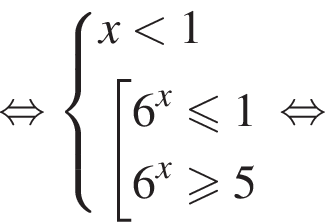












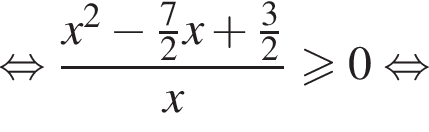









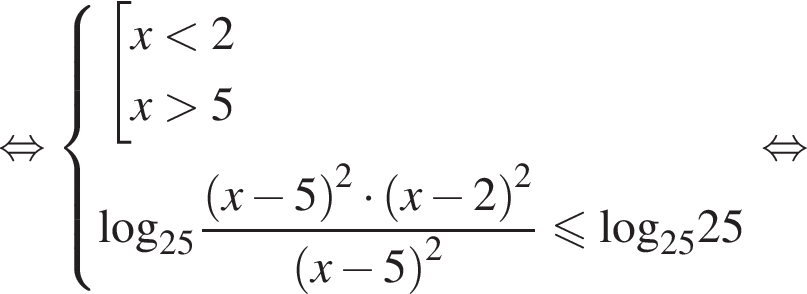


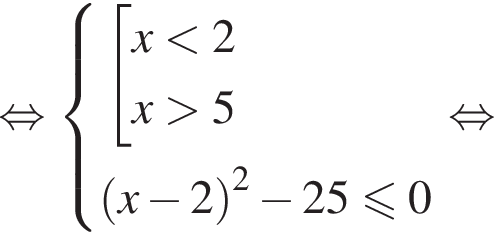



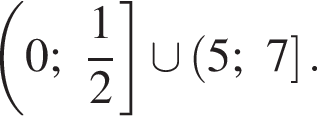

 тогда
тогда 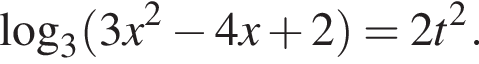 Имеем:
Имеем:





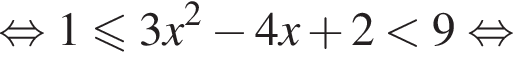

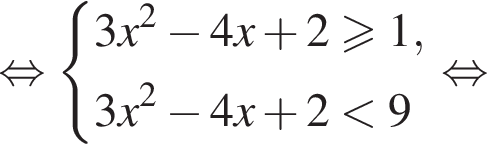



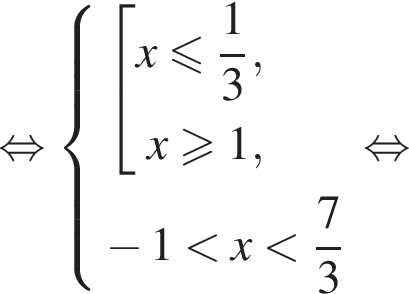
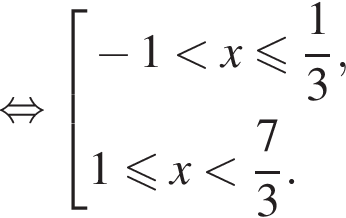

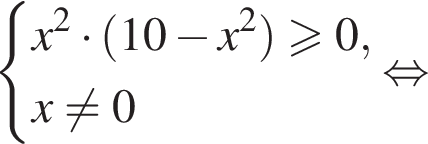




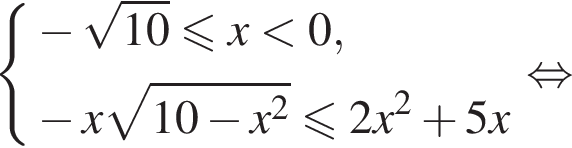

 то есть при
то есть при  Тогда решениями системы является интервал
Тогда решениями системы является интервал  Случай
Случай  не лежит во множестве решений первого неравенства. Далее,
не лежит во множестве решений первого неравенства. Далее, 
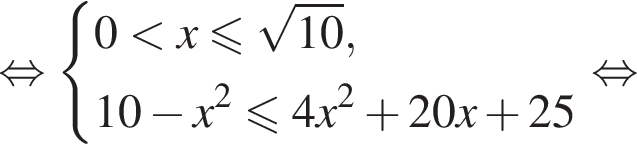
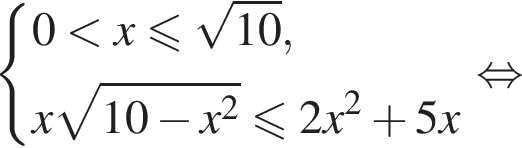
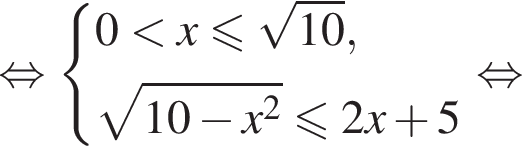





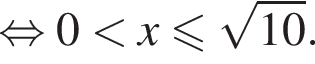

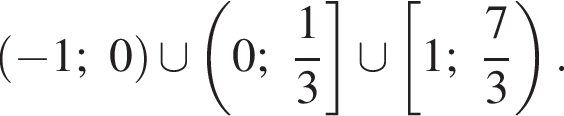

 первое неравенство системы приводится к виду
первое неравенство системы приводится к виду  Тогда
Тогда  что невозможно, или
что невозможно, или 
 Заметим, что
Заметим, что  тем самым,
тем самым, 
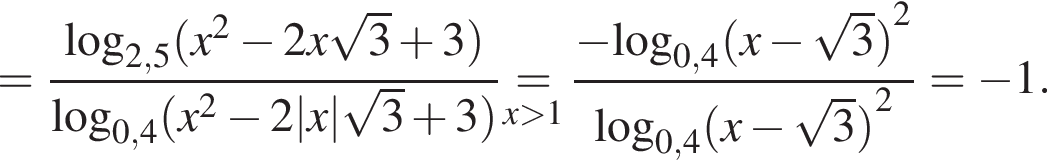



 имеем:
имеем:






 С другой стороны,
С другой стороны,  а
а  откуда
откуда