1. Тип 15 № 484579 

Классификатор алгебры: Неравенства с модулями, Неравенства смешанного типа
Методы алгебры: Введение замены
Кодификатор ФИПИ/Решу ЕГЭ:
Неравенства. Логарифмы и показательные выражения
i
Решите неравенство


Решение. Пусть  тогда неравенство принимает вид:
тогда неравенство принимает вид:


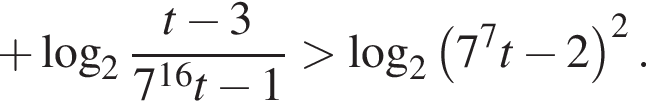
Так как  имеем
имеем  а значит,
а значит, 
Получаем:





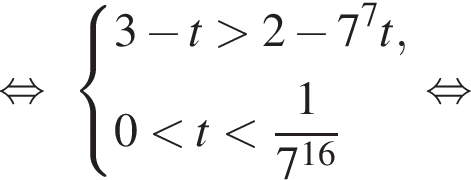

Поясним: неравенство  эквивалентно неравенству
эквивалентно неравенству 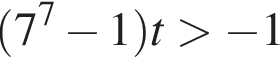 и выполнено для всех значений переменной. Итак,
и выполнено для всех значений переменной. Итак,
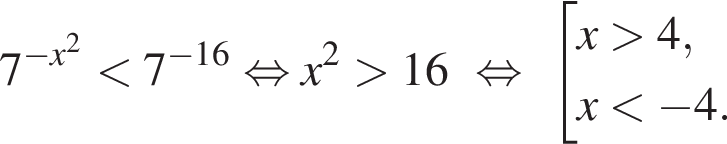
Ответ: 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 2 |
| Обоснованно получен ответ, отличающийся от верного исключением точек, ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Ответ: 

484579

Классификатор алгебры: Неравенства с модулями, Неравенства смешанного типа
Методы алгебры: Введение замены
Кодификатор ФИПИ/Решу ЕГЭ:

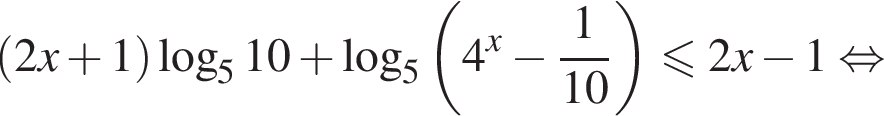





 тогда имеем:
тогда имеем:



 тогда
тогда  и неравенство принимает вид
и неравенство принимает вид
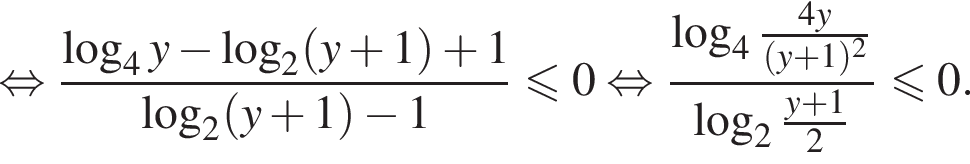



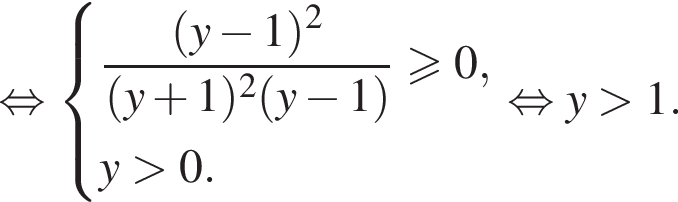


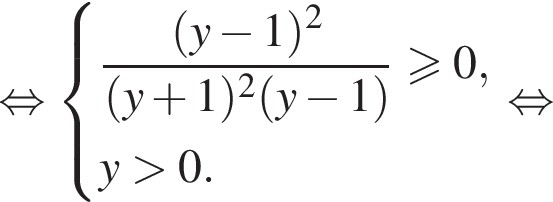



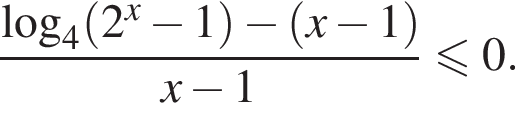
 откуда
откуда 
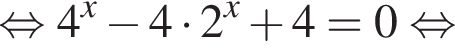






 тогда знаменатель отрицателен, числитель равен
тогда знаменатель отрицателен, числитель равен 


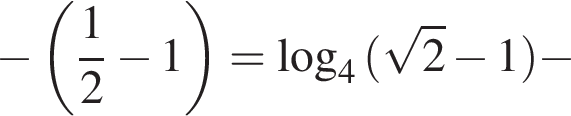

 поэтому на на промежутке (0; 1) дробь положительна.
поэтому на на промежутке (0; 1) дробь положительна. получаем
получаем





 получаем
получаем  получаем
получаем


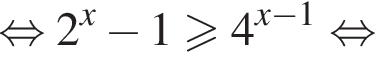




 получаем, что второй случай не даёт решений.
получаем, что второй случай не даёт решений. 
 сразу имеем x > 2. Поэтому
сразу имеем x > 2. Поэтому  Это значит, что
Это значит, что  Для первого неравенства имеем
Для первого неравенства имеем  Второе неравенство выполнено всегда, поскольку
Второе неравенство выполнено всегда, поскольку  при всех t из-за отрицательности дискриминанта (замена
при всех t из-за отрицательности дискриминанта (замена 


 на ОДЗ совпадает с знаком произведения
на ОДЗ совпадает с знаком произведения  поэтому имеем:
поэтому имеем:
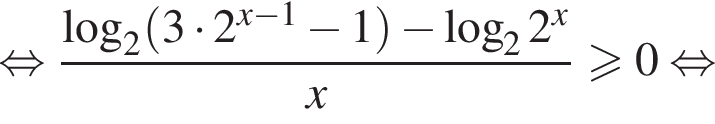













 откуда
откуда


 имеем
имеем 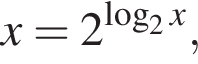 и тогда для второго слагаемого получаем
и тогда для второго слагаемого получаем 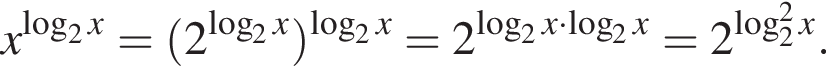









 которое логарифмированием обеих частей по основанию 2 привести к неравенству
которое логарифмированием обеих частей по основанию 2 привести к неравенству 



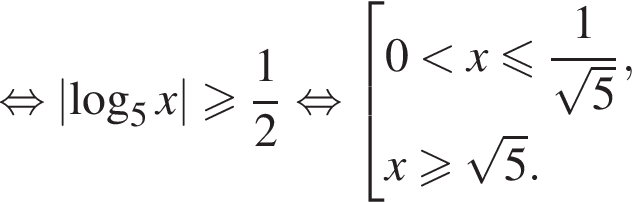






 и
и  для любого x, воспользовавшись тождеством
для любого x, воспользовавшись тождеством  заключаем, что слагаемые в левой части неравенства равны. Тогда получаем:
заключаем, что слагаемые в левой части неравенства равны. Тогда получаем:




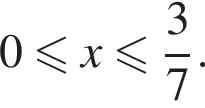



 тогда
тогда  Получаем
Получаем  откуда
откуда 

 и поэтому решением неравенства являются два промежутка:
и поэтому решением неравенства являются два промежутка: 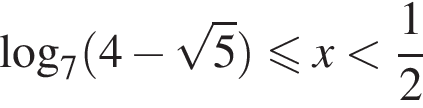 и
и 





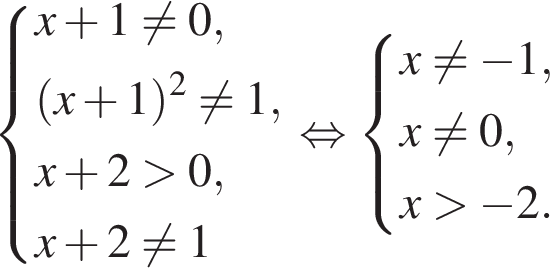
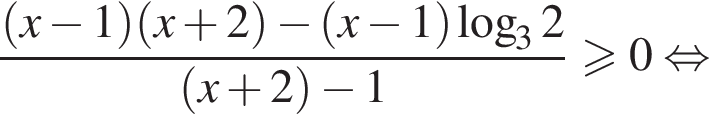
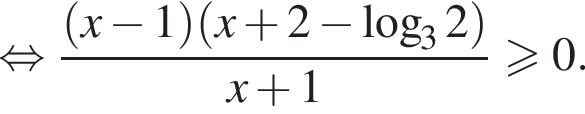
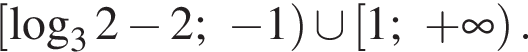

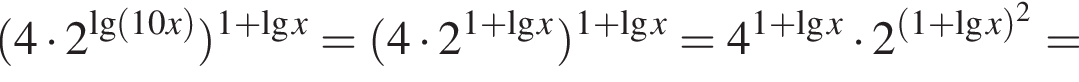

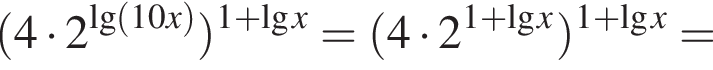
















 тогда получим
тогда получим



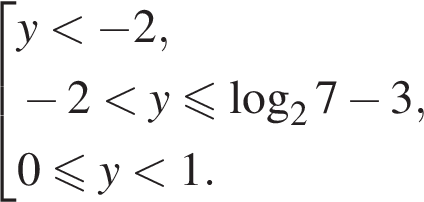



 поскольку равносильны следующие неравенства:
поскольку равносильны следующие неравенства:



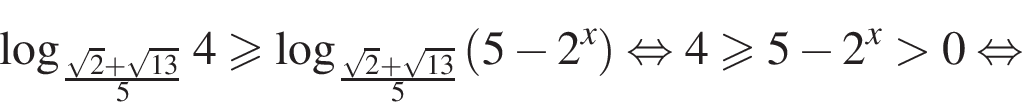











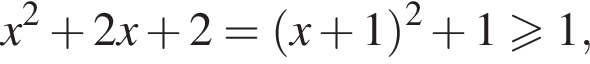 откуда
откуда  Поэтому второй множитель определен при
Поэтому второй множитель определен при  он равен нулю (и вся левая часть вместе с ним). При
он равен нулю (и вся левая часть вместе с ним). При 








 получим:
получим:

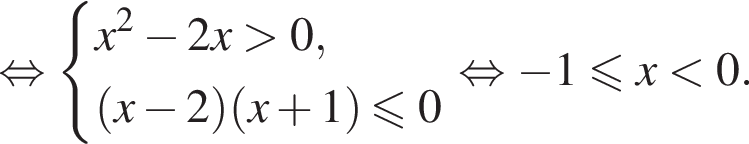














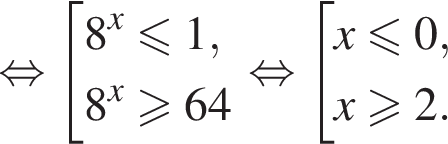


 при
при 





 откуда
откуда 














 тогда
тогда





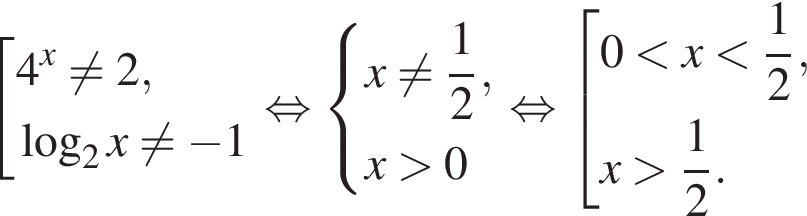






















 Тогда
Тогда









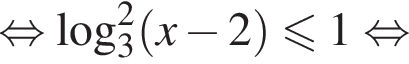




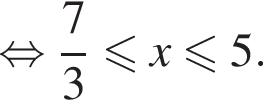



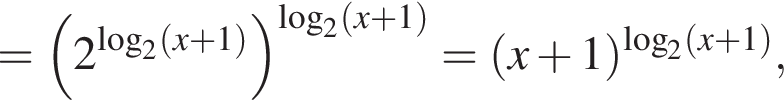



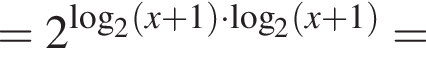





 Тогда
Тогда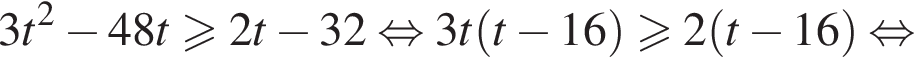









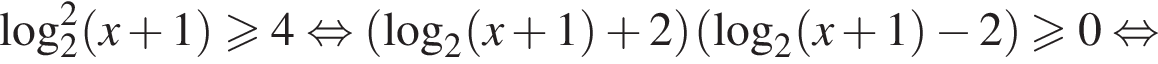








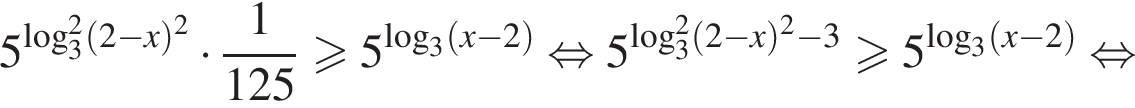






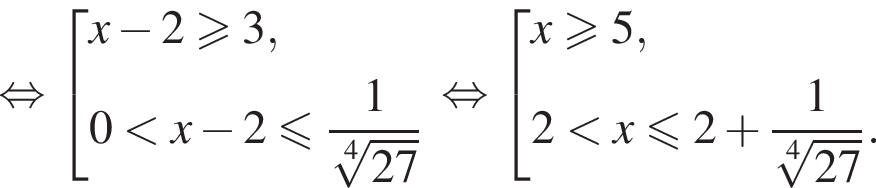



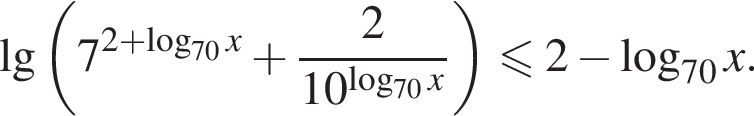











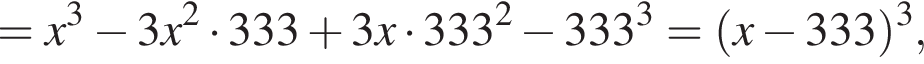



 показатель степени в левой части неравенства меньше показателя степени, стоящей в правой части неравенства:
показатель степени в левой части неравенства меньше показателя степени, стоящей в правой части неравенства:  Следовательно, неравенство верно, если основание степени не больше 1, откуда
Следовательно, неравенство верно, если основание степени не больше 1, откуда 




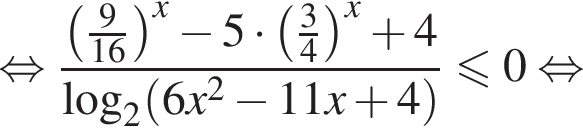
 совпадает со знаком выражения
совпадает со знаком выражения  а знак
а знак  Заметив, что
Заметив, что 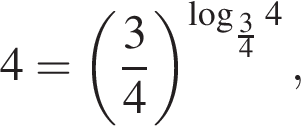 а
а  получаем:
получаем:





 разложим на множители и применим метод рационализации:
разложим на множители и применим метод рационализации:



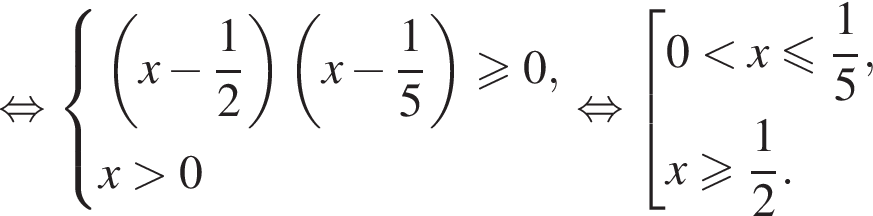











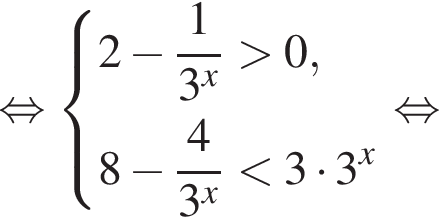
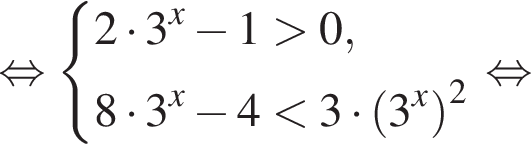























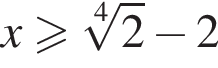 или
или 



 Неравенство записывается в виде
Неравенство записывается в виде  откуда
откуда  Возвращаясь к исходной переменной, получаем:
Возвращаясь к исходной переменной, получаем: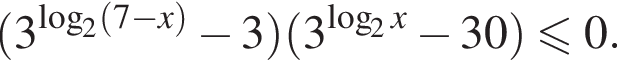
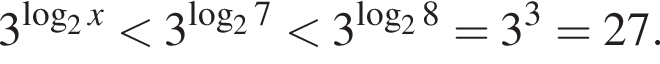





 во второй скобке получим
во второй скобке получим  откуда
откуда









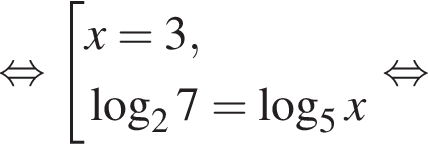
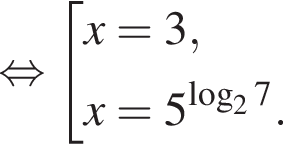
 получаем
получаем  — верно;
— верно; — неверно;
— неверно; — верно;
— верно; — неверно.
— неверно. или
или 






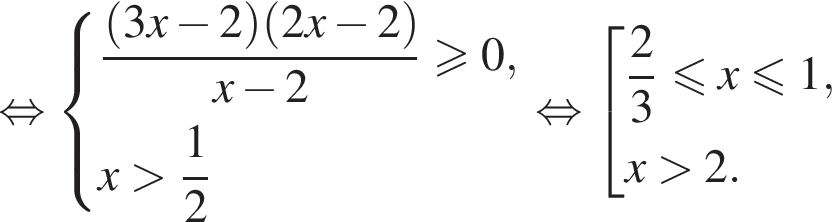


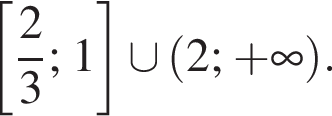


 то знаменатели отрицательны, тогда
то знаменатели отрицательны, тогда


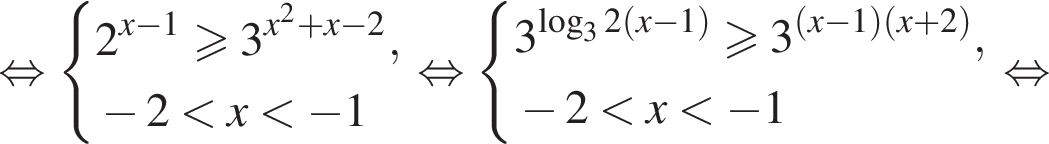
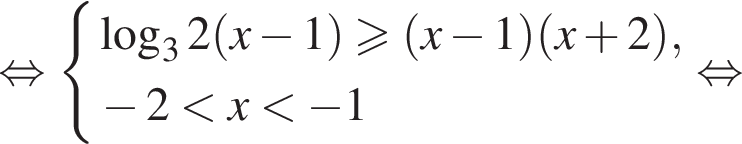
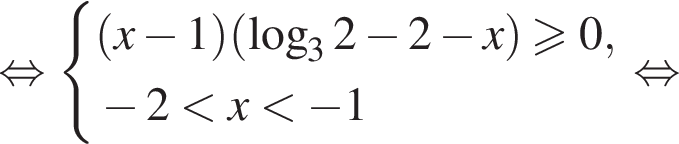





 или если
или если 



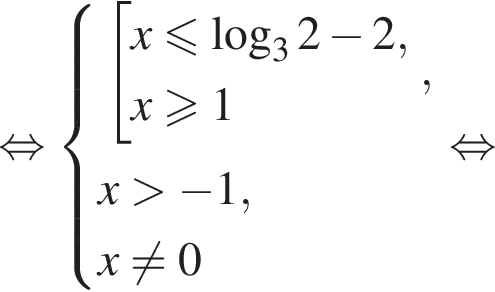












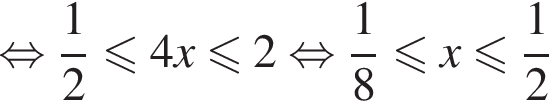






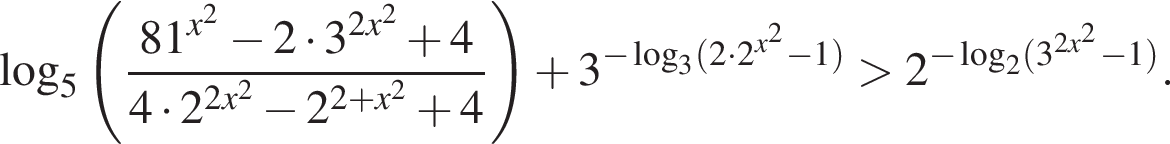

 тогда
тогда



 При
При 






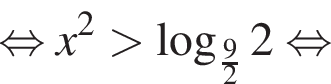





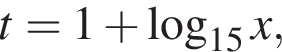 тогда
тогда












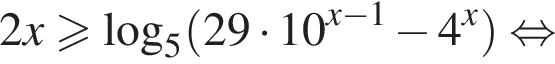




















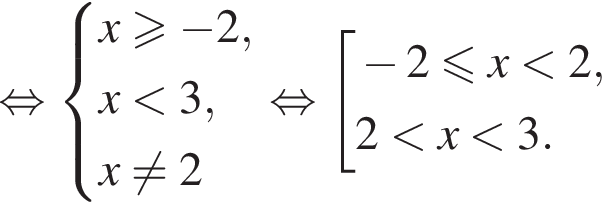
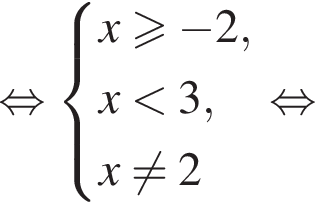


 то есть при
то есть при 





 Левая часть полученного неравенства обращается в нуль при
Левая часть полученного неравенства обращается в нуль при  или при
или при  при
при  или при
или при  или при при условии
или при при условии 



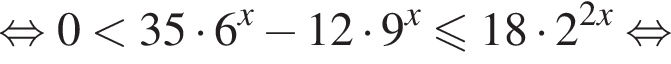



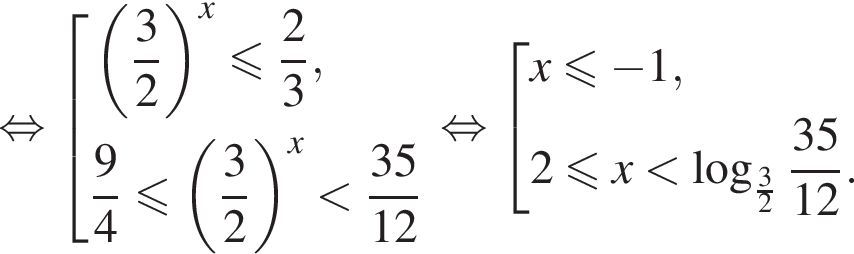

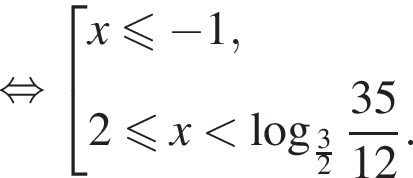

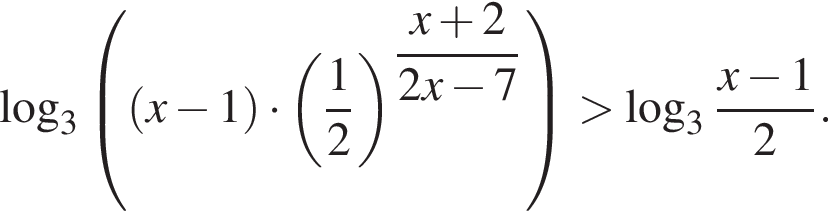


















 тогда
тогда

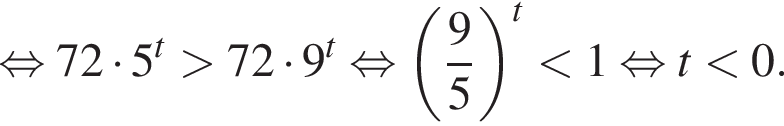








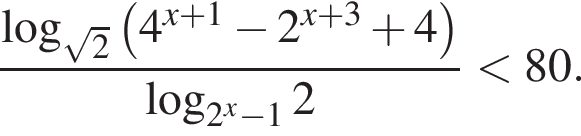

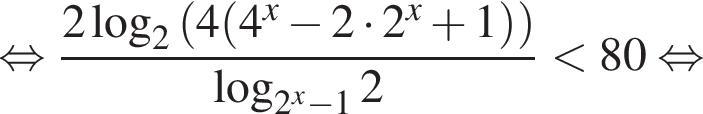




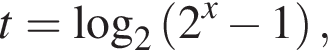 тогда
тогда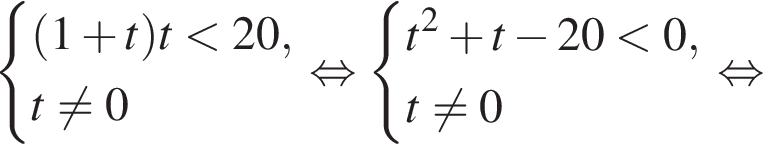









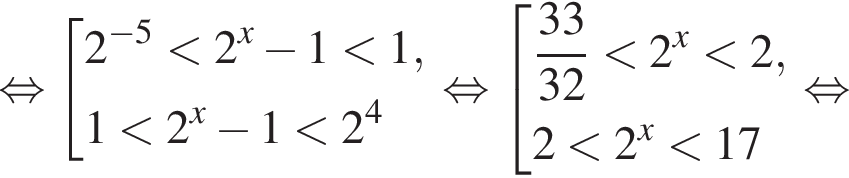






























 совпадет со знаком разности
совпадет со знаком разности 




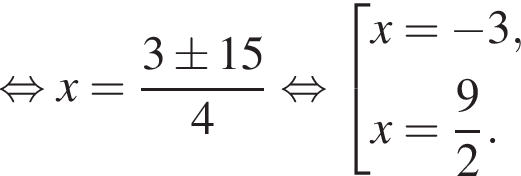

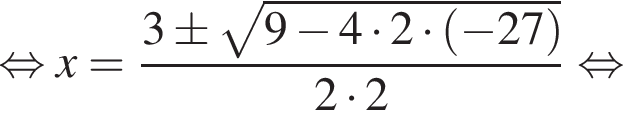








 получим квадратное неравенство, решим его:
получим квадратное неравенство, решим его:
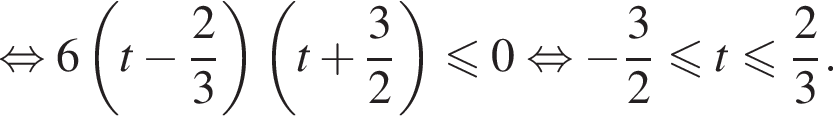




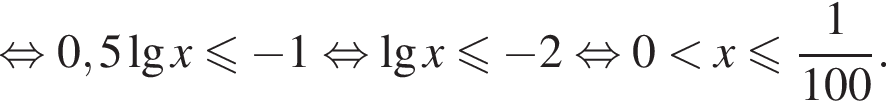







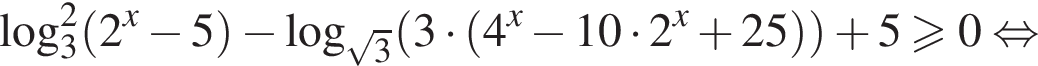







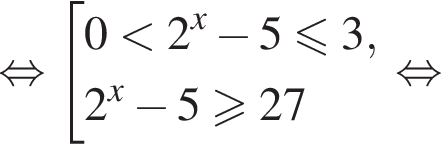





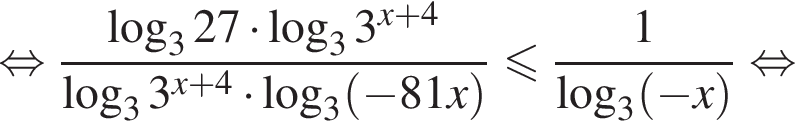
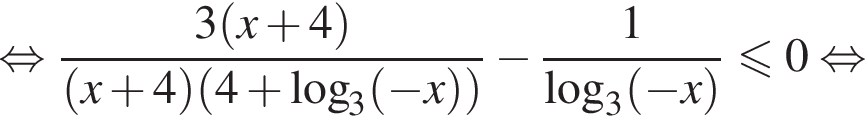

 тогда
тогда






 получаем:
получаем:
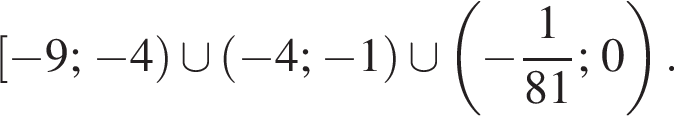

 тогда
тогда 




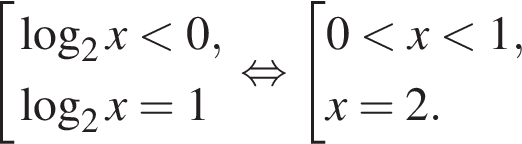




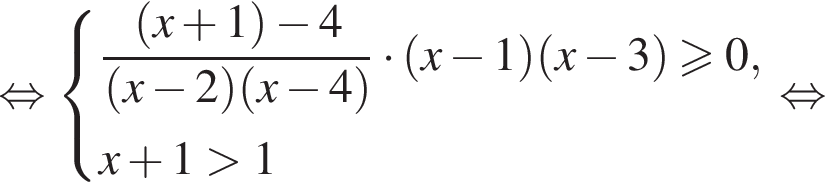





 а потому знаменатель принимает лишь отрицательные значения. Умножим обе части неравенства на знаменатель, изменив знак неравенства на противоположный:
а потому знаменатель принимает лишь отрицательные значения. Умножим обе части неравенства на знаменатель, изменив знак неравенства на противоположный:







