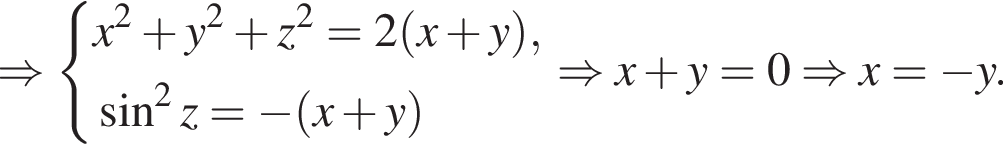Найдите все значения a, при каждом из которых уравнение  либо имеет единственное решение, либо не имеет решений.
либо имеет единственное решение, либо не имеет решений.
Решение. Пусть  тогда
тогда
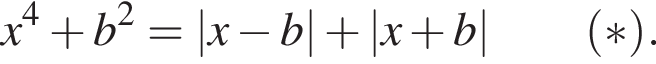
Рассмотрим два случая.
Случай 1: уравнение (⁎) имеет единственное решение. Это уравнение не изменяется при замене х на −x, а потому если число ![]() является решением этого уравнения, то и число
является решением этого уравнения, то и число ![]() также является его решением. Чтобы уравнение имело единственное решение, оно должно иметь корень
также является его решением. Чтобы уравнение имело единственное решение, оно должно иметь корень ![]() и не должно иметь других корней. Полагая
и не должно иметь других корней. Полагая ![]() находим:
находим:






Осталось проверить, имеет ли уравнение другие корни, при найденных значениях b. При ![]() уравнение принимает вид
уравнение принимает вид  и имеет три различных решения:
и имеет три различных решения:  поэтому
поэтому ![]() не подходит. Если
не подходит. Если  то
то

Раскроем модули: на отрезке [0; 2] уравнение принимает вид  и имеет единственное решение
и имеет единственное решение ![]() При
При ![]() получаем:
получаем:  Из неравенства между средним арифметическим и средним геометрическим заключаем, что
Из неравенства между средним арифметическим и средним геометрическим заключаем, что

Таким образом, при ![]() уравнение не имеет положительных корней, а потому, в силу четности левой и правой частей уравнения, не имеет и отрицательных корней, то есть имеет единственный корень
уравнение не имеет положительных корней, а потому, в силу четности левой и правой частей уравнения, не имеет и отрицательных корней, то есть имеет единственный корень ![]()
Случай 2: уравнение (⁎) не имеет решений. Поскольку значения  и
и ![]() уже разобраны, осталось рассмотреть значения
уже разобраны, осталось рассмотреть значения ![]() и
и  Обозначим
Обозначим 

Рассмотрим случай  Если
Если  то
то
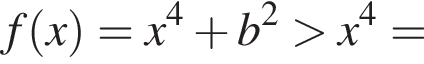

то есть уравнение решений не имеет. Если  то
то

в этом случае тоже нет решений.
Рассмотрим случай  В этом случае верны неравенства
В этом случае верны неравенства

и

поскольку  и
и 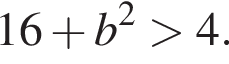 Значит, уравнение
Значит, уравнение  имеет решения отличные от нуля, то есть решений больше одного.
имеет решения отличные от нуля, то есть решений больше одного.
Таким образом, уравнение (⁎) имеет единственное решение или не имеет решений при  и
и ![]() то есть при
то есть при ![]() и
и ![]()
Ответ: 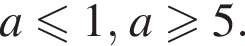
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен правильный ответ | 4 |
| С помощью верного рассуждения получено множество значений а, отличающееся от искомого конечным числом точек | 3 |
| С помощью верного рассуждения получены все граничные точки искомого множества значений а | 2 |
| Верно получена хотя бы одна граничная точка искомого множества значений а | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
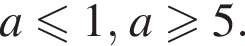
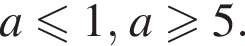


 то есть
то есть  Подставим значение
Подставим значение 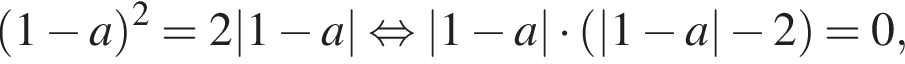


 либо
либо  или
или  Корнями этого уравнения являются числа
Корнями этого уравнения являются числа  и при
и при 
 это уравнение сводится к уравнению
это уравнение сводится к уравнению  которое не имеет корней.
которое не имеет корней. получаем уравнение
получаем уравнение  которое имеет единственный корень.
которое имеет единственный корень. которое не имеет корней.
которое не имеет корней.  и
и 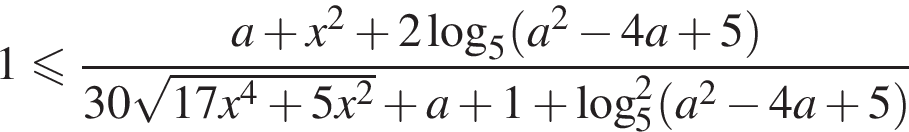













 Знаменатель положителен при a > 0, поэтому можно на него домножить обе части неравенства, не меняя его знака. Имеем:
Знаменатель положителен при a > 0, поэтому можно на него домножить обе части неравенства, не меняя его знака. Имеем:


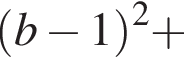
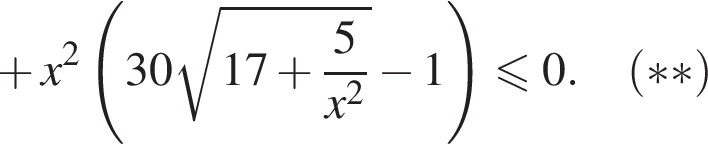
 Отсюда a = 4.
Отсюда a = 4.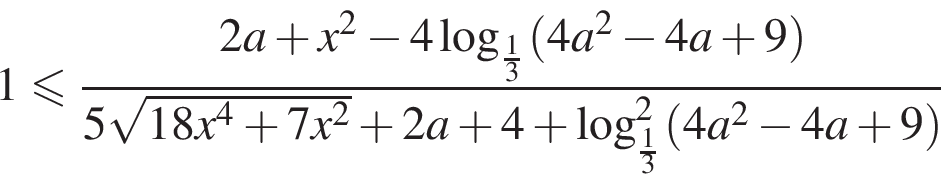








 Решим это неравенство. Поскольку знаменатель положителен, умножим на него.
Решим это неравенство. Поскольку знаменатель положителен, умножим на него.


 Решим это неравенство. Поскольку знаменатель положителен, умножим на него.
Решим это неравенство. Поскольку знаменатель положителен, умножим на него.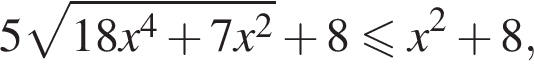
 имеет четыре решения?
имеет четыре решения?
 перепишем исходную систему в виде
перепишем исходную систему в виде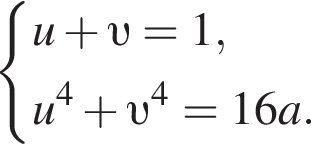
 а каждой паре положительных значений
а каждой паре положительных значений  является решением системы, то и пара
является решением системы, то и пара  — также решение этой системы, то есть исходная система получает восемь решений если
— также решение этой системы, то есть исходная система получает восемь решений если  или
или  где
где 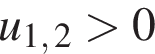 и
и 
 из второго уравнения
из второго уравнения  При найденном значении параметра система принимает вид
При найденном значении параметра система принимает вид
 Из первого уравнения
Из первого уравнения  подставим во второе:
подставим во второе:

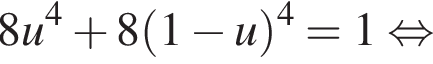






 При этом значении параметра система принимает вид
При этом значении параметра система принимает вид 



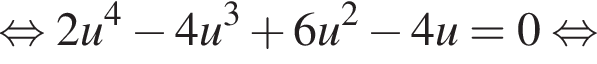



 либо имеет единственное решение, либо не имеет решений.
либо имеет единственное решение, либо не имеет решений.

 при
при  при
при 
 то
то 
 причём равенство достигается только при
причём равенство достигается только при  и
и  и
и  имеет единственное решение, то это решение
имеет единственное решение, то это решение  относительно
относительно  значит,
значит, 
 уже был разобран.
уже был разобран.
 имеет единственное решение или не имеет решений при
имеет единственное решение или не имеет решений при 


 — также решение этой системы. Поскольку система имеет единственное решение, то этим решением может быть только пара
— также решение этой системы. Поскольку система имеет единственное решение, то этим решением может быть только пара 
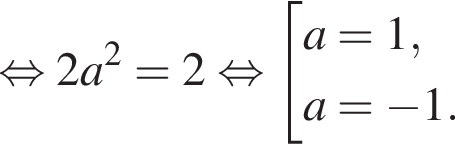


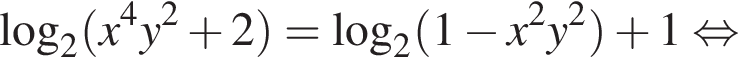



 а значит, пара (0; 1) является единственным решением системы.
а значит, пара (0; 1) является единственным решением системы. то второе уравнение системы имеет три решения:
то второе уравнение системы имеет три решения: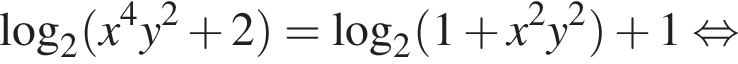






 а потому система имеет три решения.
а потому система имеет три решения. имеет единственное решение?
имеет единственное решение? — решение системы при некотором значении параметра а, то при этом значении параметра решением системы будет и
— решение системы при некотором значении параметра а, то при этом значении параметра решением системы будет и  Отсюда следует, что условие
Отсюда следует, что условие 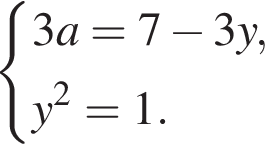
 Пусть
Пусть  Тогда система примет вид
Тогда система примет вид
 и, таким образом,
и, таким образом,  Учитывая теперь, что
Учитывая теперь, что  приходим к неравенству
приходим к неравенству

 следовательно,
следовательно,  При таком значении параметра а система перепишется в виде
При таком значении параметра а система перепишется в виде


 условию единственности решения не удовлетворяет. Заметим, что решения здесь просто угаданы.
условию единственности решения не удовлетворяет. Заметим, что решения здесь просто угаданы. 
 то есть x0 = 0. Подставим значение x = 0 в исходное уравнение:
то есть x0 = 0. Подставим значение x = 0 в исходное уравнение:


 либо
либо  или a = 5.
или a = 5.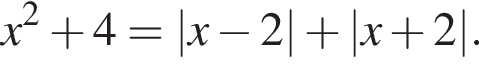
 которое не имеет корней. При a = 1 и при a = 5 исходное уравнение имеет единственный корень.
которое не имеет корней. При a = 1 и при a = 5 исходное уравнение имеет единственный корень.

 то есть
то есть 


 либо
либо  или
или 
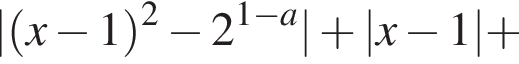

 тогда единственное решение должно иметь уравнение
тогда единственное решение должно иметь уравнение



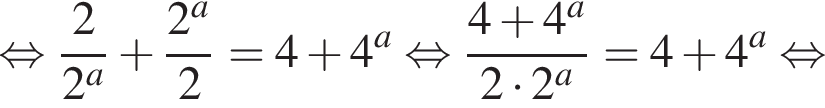



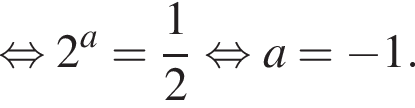
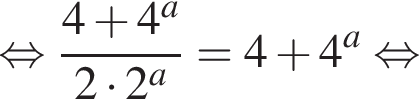

 имеем:
имеем:
 а тогда
а тогда  и уравнение принимает вид
и уравнение принимает вид  Оно, действительно, имеет единственное решение
Оно, действительно, имеет единственное решение 
 при каждом из которых система уравнений
при каждом из которых система уравнений
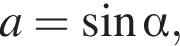 получим систему
получим систему







 Получим
Получим 
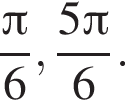





 При
При  правая часть уравнения
правая часть уравнения  При
При  правая часть уравнения равна 4, а левая часть уравнения не меньше 4, причём равенство достигается только при
правая часть уравнения равна 4, а левая часть уравнения не меньше 4, причём равенство достигается только при  Значит, исходное уравнение имеет единственное решение
Значит, исходное уравнение имеет единственное решение  Числа −2, 0 и 2 являются корнями этого уравнения.
Числа −2, 0 и 2 являются корнями этого уравнения.
 Поскольку решений должно быть два, полученные пары должны совпадать.
Поскольку решений должно быть два, полученные пары должны совпадать. то
то 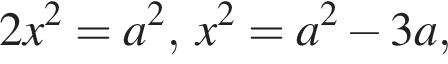 откуда
откуда
 имеет два решения. При
имеет два решения. При  Эта система имеет только одно решение.
Эта система имеет только одно решение. то
то  Тогда
Тогда  то
то  Тогда:
Тогда:  откуда
откуда 
 имеет два решения.
имеет два решения. то
то 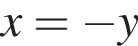 — см. случай 3.
— см. случай 3. то
то  — см. случай 2.
— см. случай 2. то
то  и, значит, система имеет единственное решение.
и, значит, система имеет единственное решение.  поскольку в этом случае ни x, ни y в ноль не обращаются. Это уравнение гиперболы.
поскольку в этом случае ни x, ни y в ноль не обращаются. Это уравнение гиперболы. 


 должно иметь единственный положительный корень. Заметим, что если оно имеет корни, то это либо два корня одного знака, либо один корень. Значит, нас интересует случай, когда его дискриминант равен нулю и единственный корень при этом положительный.
должно иметь единственный положительный корень. Заметим, что если оно имеет корни, то это либо два корня одного знака, либо один корень. Значит, нас интересует случай, когда его дискриминант равен нулю и единственный корень при этом положительный. 






 то уравнение квадратное, значит, его дискриминант должен равняться нулю:
то уравнение квадратное, значит, его дискриминант должен равняться нулю:

 откуда
откуда  Решением системы является пара
Решением системы является пара 
 получается линейное уравнение
получается линейное уравнение  которое имеет единственное решение
которое имеет единственное решение  Решением системы является пара
Решением системы является пара 


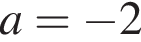 получаем уравнение
получаем уравнение  У этого уравнения решений нет.
У этого уравнения решений нет. Подставим это выражение в первое уравнение системы:
Подставим это выражение в первое уравнение системы:
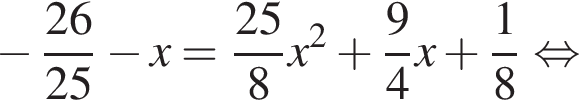

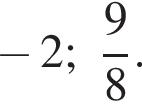


 тогда
тогда 





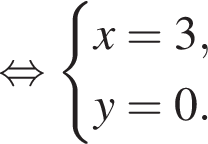




 и имеет корень
и имеет корень  Следовательно, при
Следовательно, при 














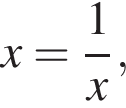 то есть при
то есть при  Найдём при каких значениях параметра a эти числа являются корнями уравнения (⁎).
Найдём при каких значениях параметра a эти числа являются корнями уравнения (⁎).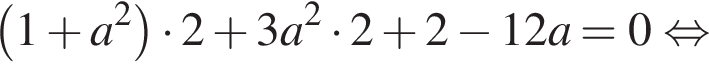





 имеем:
имеем:



 где
где  тогда
тогда  и уравнение принимает вид
и уравнение принимает вид

















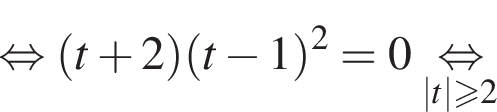

 в уравнение (⁎⁎), получим:
в уравнение (⁎⁎), получим: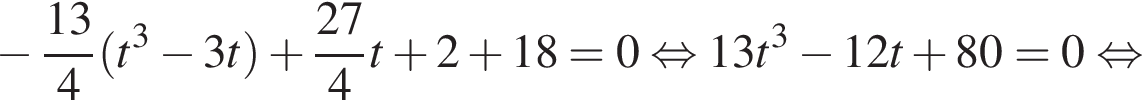
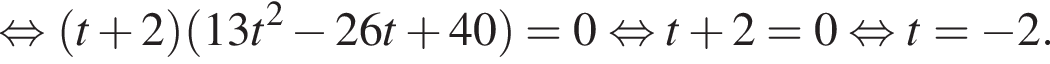





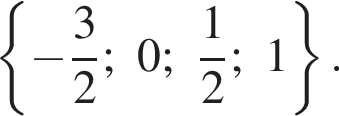
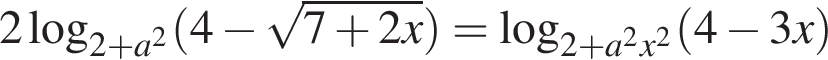
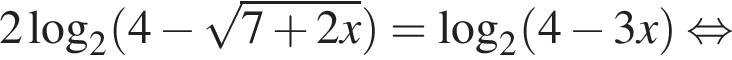






 что при любом a эквивалентно равенству 0 = 0, то есть является верным равенством для любого значения параметра.
что при любом a эквивалентно равенству 0 = 0, то есть является верным равенством для любого значения параметра.














 является решением системы, то пара чисел
является решением системы, то пара чисел  тоже является решением системы. Значит, чтобы система имела ровно три решения одним из решений должна быть пара чисел
тоже является решением системы. Значит, чтобы система имела ровно три решения одним из решений должна быть пара чисел  Подставив
Подставив  во второе уравнение системы, получаем, что решением должна являться или пара чисел
во второе уравнение системы, получаем, что решением должна являться или пара чисел  или пара чисел
или пара чисел  Из первого уравнения системы найдём значения параметра, при которых эти пары чисел являются решениями системы. Если
Из первого уравнения системы найдём значения параметра, при которых эти пары чисел являются решениями системы. Если  если же
если же  то
то  Таким образом, только при этих значениях параметра у системы может быть нечётное число решений. Выясним, сколько решений имеет система при найденных значениях параметра.
Таким образом, только при этих значениях параметра у системы может быть нечётное число решений. Выясним, сколько решений имеет система при найденных значениях параметра. в первое уравнение системы:
в первое уравнение системы:





 и
и 
 в первое уравнение системы:
в первое уравнение системы: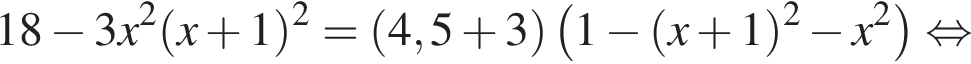
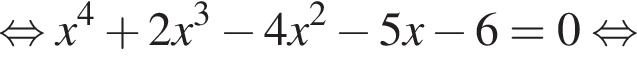







 является решением, то и число
является решением, то и число  также является решением.
также является решением.



 то уравнение имеет вид
то уравнение имеет вид
 а
а 

 а
а 






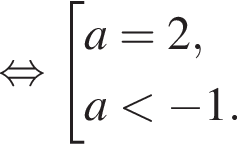
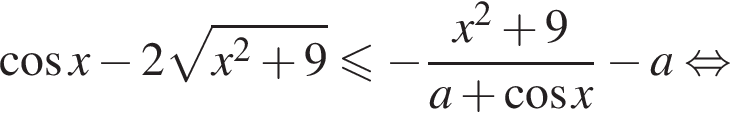



 знаменатель левой части отрицателен, тогда необходимо выполнение неравенства
знаменатель левой части отрицателен, тогда необходимо выполнение неравенства


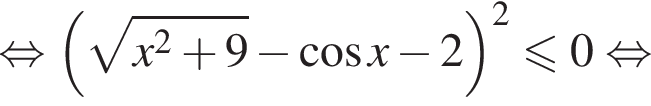




 тогда каждому значению переменной x соответствует ровно одно значение переменной t, а исходное уравнение и уравнение
тогда каждому значению переменной x соответствует ровно одно значение переменной t, а исходное уравнение и уравнение





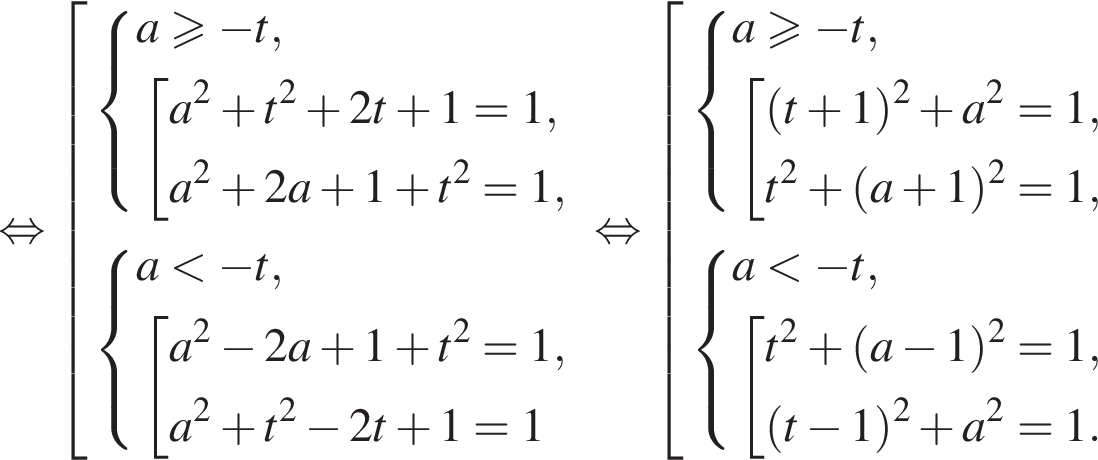

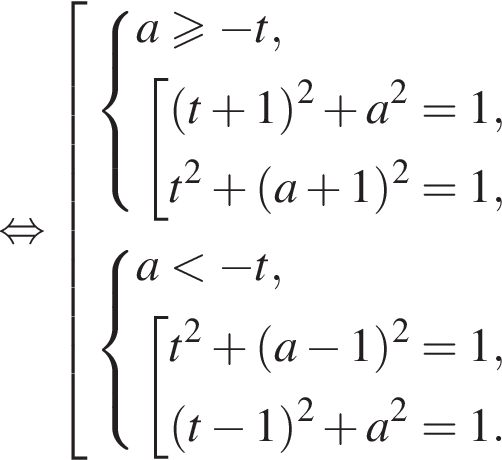


 — имеют два решения, при
— имеют два решения, при 
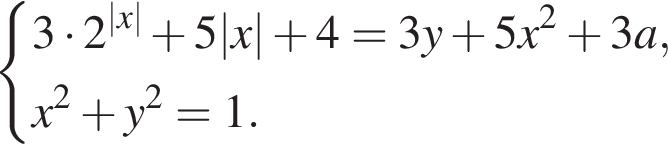
 тоже является решением системы. Значит, чтобы решение было единственным, необходимо, чтобы
тоже является решением системы. Значит, чтобы решение было единственным, необходимо, чтобы  С учётом второго уравнения системы получаем, что единственным решением может являться либо пара чисел
С учётом второго уравнения системы получаем, что единственным решением может являться либо пара чисел 
 Проверим есть ли другие решения при этом значении параметра. Подставляя найденное значение параметра, находим:
Проверим есть ли другие решения при этом значении параметра. Подставляя найденное значение параметра, находим: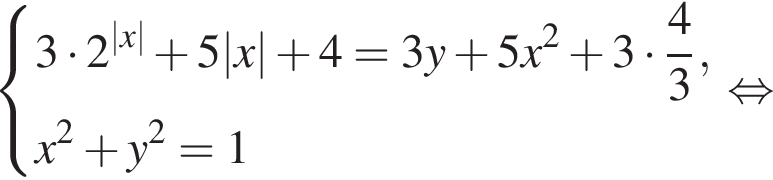

 и
и  тогда левая часть первого уравнения системы неотрицательна, а правая неположительна, причём равенство достигается только при
тогда левая часть первого уравнения системы неотрицательна, а правая неположительна, причём равенство достигается только при  является решением системы при
является решением системы при  Подставляя найденное значение параметра, находим:
Подставляя найденное значение параметра, находим:

 система имеет более одного решения.
система имеет более одного решения.

 является решением системы, то тройка чисел
является решением системы, то тройка чисел  тоже является решением системы. Значит, чтобы решение было единственным, должно выполняться равенство
тоже является решением системы. Значит, чтобы решение было единственным, должно выполняться равенство 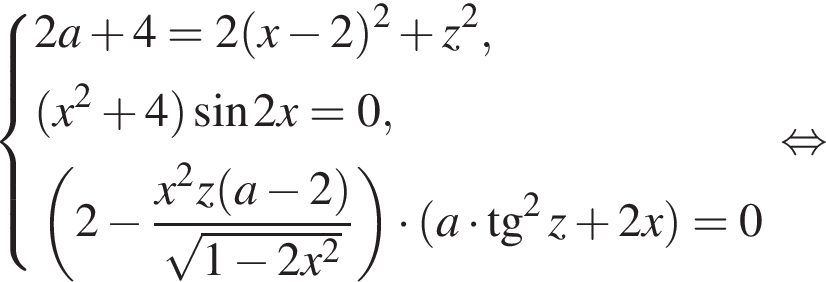



 является решением системы, то тройка чисел
является решением системы, то тройка чисел  тоже является решением системы. Значит, чтобы решение было единственным, должно выполняться равенство
тоже является решением системы. Значит, чтобы решение было единственным, должно выполняться равенство  Таким образом, единственным решением системы может быть только тройка чисел
Таким образом, единственным решением системы может быть только тройка чисел  Эта тройка чисел является решением системы при
Эта тройка чисел является решением системы при 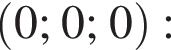


 а графиком уравнения (⁎⁎) — прямая
а графиком уравнения (⁎⁎) — прямая  которая касается этой окружности в точке
которая касается этой окружности в точке  Если она лежит на сфере, ее координаты должны удовлетворять условию
Если она лежит на сфере, ее координаты должны удовлетворять условию то есть
то есть  Тогда
Тогда  однако из уравнения
однако из уравнения  следует, что
следует, что  Значит,
Значит,  и тогда из третьего уравнения следует, что
и тогда из третьего уравнения следует, что  и
и  откуда
откуда  то есть при
то есть при 


 Из формулы
Из формулы  находим:
находим: 




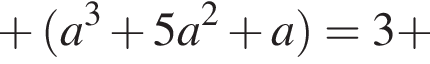
 корень уравнения, то и
корень уравнения, то и  — тоже корень. Чтобы уравнение имело единственный корень, оно должно иметь решением
— тоже корень. Чтобы уравнение имело единственный корень, оно должно иметь решением 
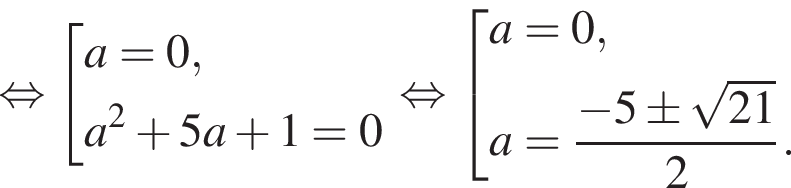
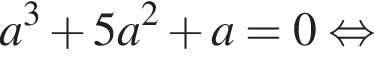



 и равенство достигается при
и равенство достигается при 
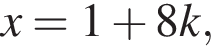



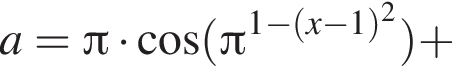

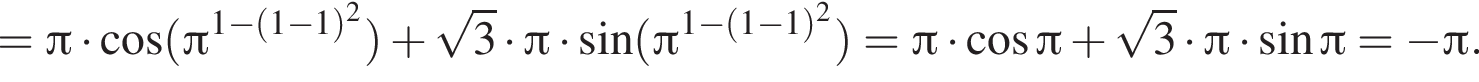
 Для этого решим уравнение:
Для этого решим уравнение:
















 исходное уравнение имеет одно решение.
исходное уравнение имеет одно решение.

 условие будет выполнено, значит, чтобы решение было единственным, необходимо, чтобы выполнялось условие
условие будет выполнено, значит, чтобы решение было единственным, необходимо, чтобы выполнялось условие  удовлетворяет неравенству
удовлетворяет неравенству 

 другие решения системы. Решим систему при
другие решения системы. Решим систему при 






 рассмотрим квадратичную функцию
рассмотрим квадратичную функцию  Заметим, что
Заметим, что 


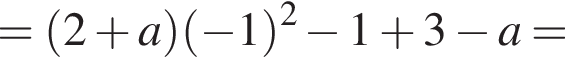
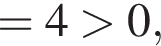

 имеет два корня, то они по модулю либо оба больше 1, либо оба меньше 1. Значит, условие задачи не может быть выполнено. Если уравнение
имеет два корня, то они по модулю либо оба больше 1, либо оба меньше 1. Значит, условие задачи не может быть выполнено. Если уравнение 





 единственным корнем уравнения (⁎) является
единственным корнем уравнения (⁎) является
 единственным корнем уравнения (⁎) является
единственным корнем уравнения (⁎) является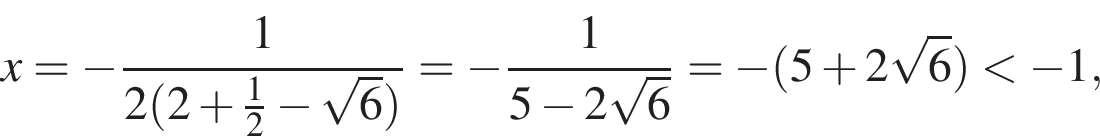




 Решим систему при
Решим систему при 




 то левая часть второго уравнения полученной системы положительна, значит, второе уравнение и вся система не имеют решений. Тогда при
то левая часть второго уравнения полученной системы положительна, значит, второе уравнение и вся система не имеют решений. Тогда при  и условие задачи выполнено.
и условие задачи выполнено.

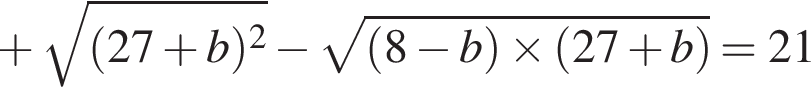

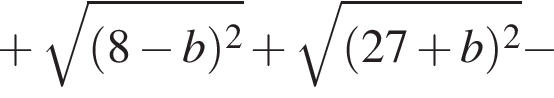





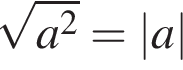 получаем:
получаем:










 уравнение не имеет других корней:
уравнение не имеет других корней:










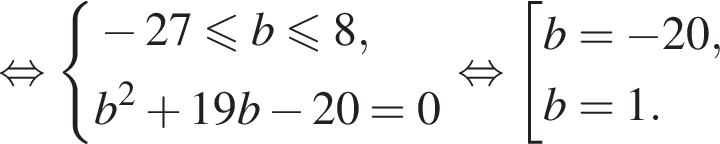



 значит, это значение b не подходит. При
значит, это значение b не подходит. При 

 является решением системы, то и тройка чисел
является решением системы, то и тройка чисел  является ее решением. Чтобы система имела единственное решение, должно быть выполнено равенство
является ее решением. Чтобы система имела единственное решение, должно быть выполнено равенство  Положим,
Положим, 
 является ее решением. Чтобы система имела единственное решение, должно быть выполнено равенство
является ее решением. Чтобы система имела единственное решение, должно быть выполнено равенство  Положим,
Положим, 
 то есть
то есть 
 а значит,
а значит,  откуда
откуда  Таким образом, единственным возможным значением параметра является
Таким образом, единственным возможным значением параметра является