
Найдите все значения параметра a, при каждом из которых уравнение

имеет один корень на отрезке [0; 1].
Решение. Преобразуем уравнение:
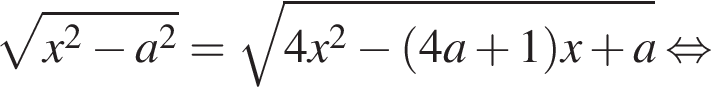



В системе координат xOa графиками уравнений являются прямые ![]() и
и  При неотрицательных значениях x неравенству
При неотрицательных значениях x неравенству  удовлетворяют точки лежащие одновременно не ниже прямой
удовлетворяют точки лежащие одновременно не ниже прямой  и не выше прямой
и не выше прямой ![]() Решение полученной системы на отрезке [0; 1] выделено оранжевым цветом. Абсциссы точек A и B пересечения прямых найдём из уравнений:
Решение полученной системы на отрезке [0; 1] выделено оранжевым цветом. Абсциссы точек A и B пересечения прямых найдём из уравнений:


Откуда 


Анализируя график, получаем, что исходное уравнение на отрезке [0; 1]:
— при  не имеет корней;
не имеет корней;
— при  имеет один корень;
имеет один корень;
— при  имеет два корня;
имеет два корня;
— при  имеет один корень;
имеет один корень;
— при ![]() не имеет корней.
не имеет корней.
Таким образом, исходное уравнение на отрезке [0; 1] имеет один корень при  или при
или при 
Ответ: 
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 4 |
| С помощью верного рассуждения получены верные значения параметра, но допущен недочет | 3 |
| С помощью верного рассуждения получен неверный ответ из-за вычислительной ошибки, при этом верно выполнены все шаги решения, ИЛИ в решении верно найдены все граничные точки множества значений параметра, но неверно определены промежутки значений | 2 |
| В случае аналитического решения: задача верно сведена к набору решенных уравнений и неравенств с учетом требуемых ограничений, ИЛИ в случае графического решения: задача верно сведена к исследованию взаимного расположения линий (изображены необходимые фигуры, учтены ограничения, указана связь исходной задачи с построенными фигурами) | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |





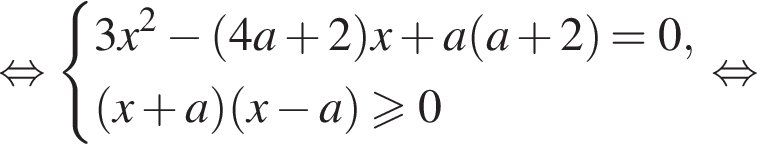

 При неотрицательных значениях x неравенству
При неотрицательных значениях x неравенству 
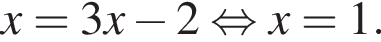
 и
и 
 не имеет корней;
не имеет корней;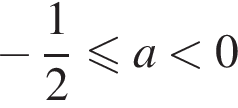 имеет один корень;
имеет один корень; имеет два корня;
имеет два корня;




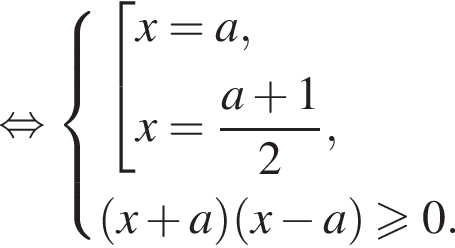
 При неотрицательных значениях x неравенству
При неотрицательных значениях x неравенству 


 не имеет корней;
не имеет корней; имеет один корень;
имеет один корень;

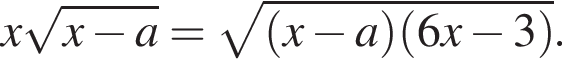
 Получаем
Получаем  при условии
при условии 


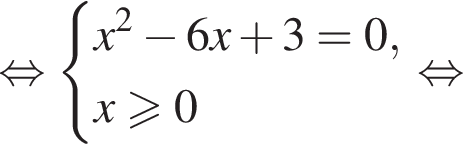


 условие принимает вид
условие принимает вид  откуда
откуда  То есть в этом случае
То есть в этом случае 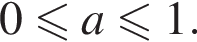
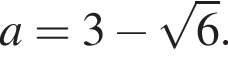

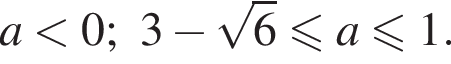
 при
при  и
и 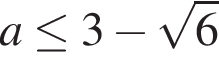 ,
, или с учетом принадлежности корней указанному отрезку:
или с учетом принадлежности корней указанному отрезку: 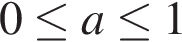 и
и 




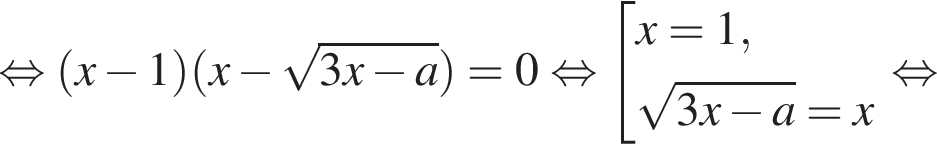






 Решение полученной совокупности на отрезке [0; 1] выделено оранжевым цветом. Ключевыми для ответа на вопрос задачи являются ординаты точек
Решение полученной совокупности на отрезке [0; 1] выделено оранжевым цветом. Ключевыми для ответа на вопрос задачи являются ординаты точек 


 имеет два корня;
имеет два корня; имеет один корень;
имеет один корень;





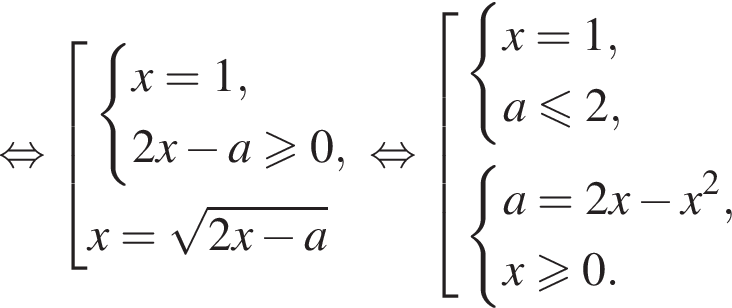


 Решение полученной совокупности выделено оранжевым цветом. Ключевыми для ответа на вопрос задачи являются ординаты точек
Решение полученной совокупности выделено оранжевым цветом. Ключевыми для ответа на вопрос задачи являются ординаты точек  и
и 
 имеет один корень;
имеет один корень;





 Тогда корень
Тогда корень  принадлежит отрезку [4; 8] и удовлетворяет ОДЗ. Тогда уравнение имеет единственное решение на заданном отрезке, если второй корень не принадлежит отрезку [4; 8] или не удовлетворяет ОДЗ. Имеем:
принадлежит отрезку [4; 8] и удовлетворяет ОДЗ. Тогда уравнение имеет единственное решение на заданном отрезке, если второй корень не принадлежит отрезку [4; 8] или не удовлетворяет ОДЗ. Имеем:




 принадлежит отрезку [4; 8] и удовлетворяет ОДЗ. Тогда уравнение имеет единственное решение на заданном отрезке, если первый корень не принадлежит отрезку [4; 8] или не удовлетворяет ОДЗ. Имеем:
принадлежит отрезку [4; 8] и удовлетворяет ОДЗ. Тогда уравнение имеет единственное решение на заданном отрезке, если первый корень не принадлежит отрезку [4; 8] или не удовлетворяет ОДЗ. Имеем:





 и
и  лежащие внутри круга, ограниченного окружностью
лежащие внутри круга, ограниченного окружностью 


 найдём, подставив в уравнение окружности
найдём, подставив в уравнение окружности 






 имеет ровно один корень.
имеет ровно один корень. На отрезке
На отрезке  если
если  и не принадлежит данному отрезку при прочих значениях параметра. Таким образом, исходное уравнение имеет ровно один корень на отрезке
и не принадлежит данному отрезку при прочих значениях параметра. Таким образом, исходное уравнение имеет ровно один корень на отрезке  и
и 

 имеет ровно четыре различных решения.
имеет ровно четыре различных решения.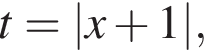 при этом
при этом  Исходное уравнение имеет ровно четыре различных решения, тогда и только тогда, когда полученное уравнение является квадратным и имеет два положительных корня. Тогда
Исходное уравнение имеет ровно четыре различных решения, тогда и только тогда, когда полученное уравнение является квадратным и имеет два положительных корня. Тогда  то есть
то есть  откуда
откуда 













 c концом в точке
c концом в точке  во втором — прямую l, задаваемую уравнением х = 3, в третьем — дугу
во втором — прямую l, задаваемую уравнением х = 3, в третьем — дугу  с концом в точке А (см. рис.).
с концом в точке А (см. рис.).  и
и  как квадратные относительно x и найдем, при каких значениях параметра их дискриминанты обращаются в нуль. Тем самым, при
как квадратные относительно x и найдем, при каких значениях параметра их дискриминанты обращаются в нуль. Тем самым, при  и
и  имеет две общие точки с дугой
имеет две общие точки с дугой  имеет одну общую точку с дугой
имеет одну общую точку с дугой  и
и 


 или
или  ; возможно, с включением граничных точек
; возможно, с включением граничных точек
 и
и  Первый график — парабола
Первый график — парабола  и второй — прямая
и второй — прямая  разбивают полуплоскость на 4 части, в двух из которых (выделены зелёным) неравенство выполняется.
разбивают полуплоскость на 4 части, в двух из которых (выделены зелёным) неравенство выполняется.  является пучок прямых
является пучок прямых  проходящих через точку с координатами
проходящих через точку с координатами 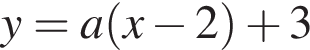 имеет только одну общую точку с выделенными зелёным частями плоскости. Это достигается в двух случаях.
имеет только одну общую точку с выделенными зелёным частями плоскости. Это достигается в двух случаях.  (выделено оранжевым). Тогда
(выделено оранжевым). Тогда 
 должно иметь единственное решение. Запишем его в виде
должно иметь единственное решение. Запишем его в виде  и найдем дискриминант:
и найдем дискриминант:


 или
или  При
При  абсцисса точки касания положительна, что не соответствует условию задачи. При
абсцисса точки касания положительна, что не соответствует условию задачи. При 
 не имеет решений;
не имеет решений; имеет бесконечное число решений;
имеет бесконечное число решений; имеет одно решение;
имеет одно решение;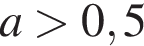 имеет бесконечное число решений.
имеет бесконечное число решений.


 его графиком являются две параболы, симметричные относительно оси абсцисс, с общими точками (0; 0) и (2; 0).
его графиком являются две параболы, симметричные относительно оси абсцисс, с общими точками (0; 0) и (2; 0).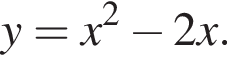 Решим соответствующее уравнение и найдём нуль дискриминанта:
Решим соответствующее уравнение и найдём нуль дискриминанта:
 он равен нулю при
он равен нулю при  откуда
откуда 
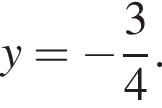
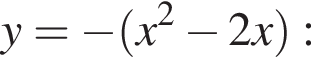

 он равен нулю при
он равен нулю при  откуда
откуда 

 то у прямой y = a – x нет общих точек с графиком
то у прямой y = a – x нет общих точек с графиком  а с графиком
а с графиком  — две общие точки.
— две общие точки.  то у прямой y = a – x одна общая точка
то у прямой y = a – x одна общая точка  с графиком
с графиком  значит, будет 3 общих точки.
значит, будет 3 общих точки. то прямая y = a – x пересекает каждую параболу в двух точках, которые не могут совпасть полностью, так как это происходит в точках (0; 0) и (2; 0), поэтому будет минимум 3 решения.
то прямая y = a – x пересекает каждую параболу в двух точках, которые не могут совпасть полностью, так как это происходит в точках (0; 0) и (2; 0), поэтому будет минимум 3 решения. то у прямой y = a – x одна общая точка
то у прямой y = a – x одна общая точка  с графиком
с графиком  то у прямой y = a – x нет общих точек с графиком
то у прямой y = a – x нет общих точек с графиком 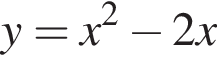 — две общие точки.
— две общие точки. 

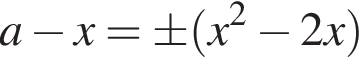 имело равно два различных решения.
имело равно два различных решения.
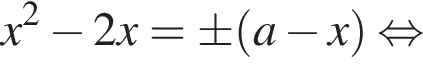

 дискриминант уравнения (2) равен
дискриминант уравнения (2) равен  его корни
его корни 


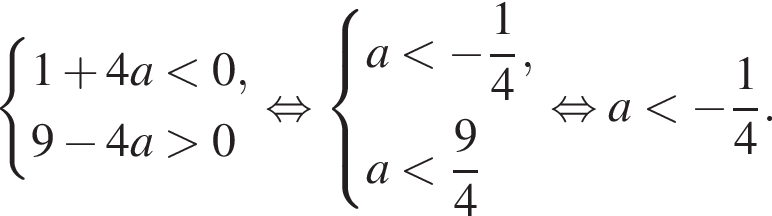

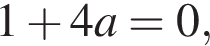 значит,
значит,  Необходимо, чтобы
Необходимо, чтобы 

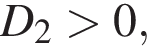 x1 = x3, x2 = x4:
x1 = x3, x2 = x4: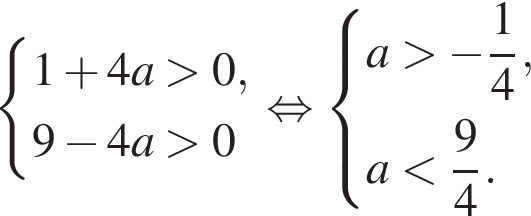


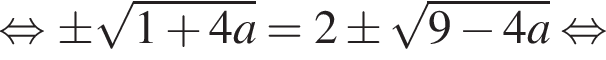










 — не подходит.
— не подходит.




 значит,
значит, 
 — не подходит.
— не подходит.
 — не подходит.
— не подходит.

 его графиком являются две параболы, симметричные относительно оси абсцисс, с общими точками (0; 0) и (4; 0).
его графиком являются две параболы, симметричные относительно оси абсцисс, с общими точками (0; 0) и (4; 0). является касательной к графику
является касательной к графику  Решим соответствующее уравнение и найдём нуль дискриминанта:
Решим соответствующее уравнение и найдём нуль дискриминанта:
 он равен нулю при
он равен нулю при  откуда
откуда 


 он равен нулю при
он равен нулю при 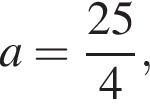 откуда
откуда 

 то у прямой
то у прямой  а с графиком
а с графиком  — две общие точки.
— две общие точки. 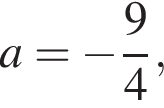 то у прямой
то у прямой  с графиком
с графиком  значит, будет 3 общих точки.
значит, будет 3 общих точки. то прямая
то прямая  то у прямой
то у прямой  с графиком
с графиком 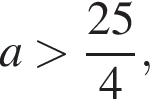 то у прямой
то у прямой  — две общие точки.
— две общие точки. 
 имело равно два различных решения.
имело равно два различных решения.
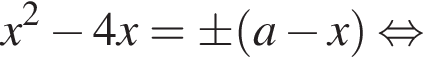

 дискриминант уравнения (2) равен
дискриминант уравнения (2) равен  его корни
его корни 

 значит,
значит,  Необходимо, чтобы
Необходимо, чтобы 





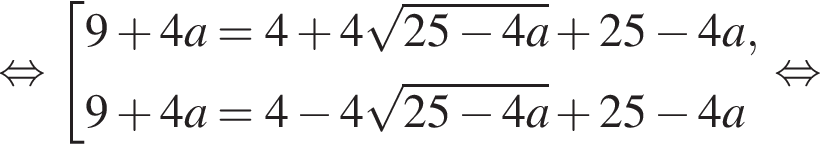










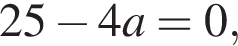 значит,
значит,  Необходимо, чтобы
Необходимо, чтобы 



 его графиком являются две параболы, симметричные относительно оси абсцисс, с общими точками (0; 0) и (−2; 0).
его графиком являются две параболы, симметричные относительно оси абсцисс, с общими точками (0; 0) и (−2; 0).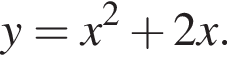 Решим соответствующее уравнение и найдём нуль дискриминанта:
Решим соответствующее уравнение и найдём нуль дискриминанта:
 он равен нулю при
он равен нулю при 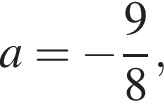 откуда
откуда 


 он равен нулю при
он равен нулю при  откуда
откуда 
 то у прямой y = 2a – x нет общих точек с графиком
то у прямой y = 2a – x нет общих точек с графиком  а с графиком
а с графиком  — две общие точки.
— две общие точки.  то у прямой y = 2a – x одна общая точка
то у прямой y = 2a – x одна общая точка  с графиком
с графиком  значит, будет 3 общих точки.
значит, будет 3 общих точки. то прямая y = 2a – x пересекает каждую параболу в двух точках, которые не могут совпасть полностью, так как это происходит в точках (0; 0) и (−2; 0), поэтому будет минимум 3 решения.
то прямая y = 2a – x пересекает каждую параболу в двух точках, которые не могут совпасть полностью, так как это происходит в точках (0; 0) и (−2; 0), поэтому будет минимум 3 решения. то у прямой y = 2a – x одна общая точка
то у прямой y = 2a – x одна общая точка  с графиком
с графиком  то у прямой y = 2a – x нет общих точек с графиком
то у прямой y = 2a – x нет общих точек с графиком  — две общие точки.
— две общие точки. 

 имело равно два различных решения.
имело равно два различных решения.

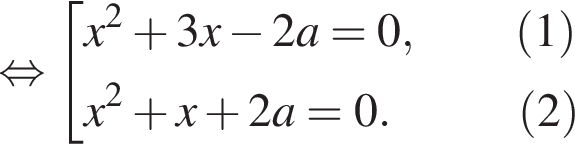
 дискриминант уравнения (2) равен
дискриминант уравнения (2) равен  его корни
его корни 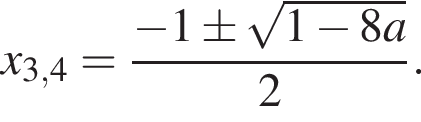

 значит,
значит,  Необходимо, чтобы
Необходимо, чтобы 

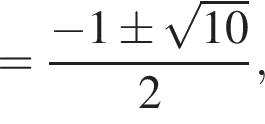



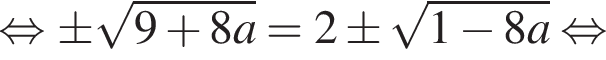




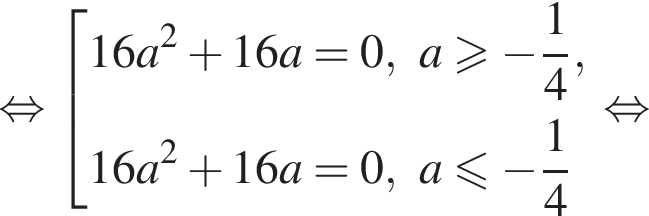




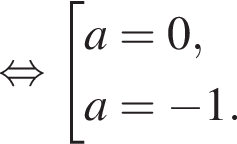


 значит,
значит, 


 получают сдвигом графика функции
получают сдвигом графика функции 
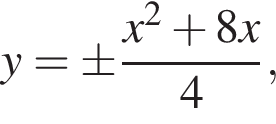 построенных на отрезке [−8; 0].
построенных на отрезке [−8; 0]. касается левой и правой ветвей графика функции
касается левой и правой ветвей графика функции  то есть прямых
то есть прямых 
 соответственно. Найдем
соответственно. Найдем 


 Дискриминант обращается в нуль при
Дискриминант обращается в нуль при  При этом абсцисса точки касания
При этом абсцисса точки касания  удовлетворяет условию
удовлетворяет условию  Аналогично найдем
Аналогично найдем 


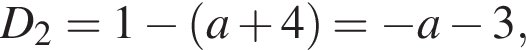 он обращается в нуль при
он обращается в нуль при  При этом абсцисса точки касания
При этом абсцисса точки касания  удовлетворяет условию
удовлетворяет условию 



 графики пересекаются ровно в трех точках. При
графики пересекаются ровно в трех точках. При  и
и  графики пересекаются в ровно в четырех точках. При
графики пересекаются в ровно в четырех точках. При  и при
и при  одна из ветвей графика модуля не пересекается с графиком второго уравнения, а другая ветвь имеет с ним не больше двух точек пересечения, поэтому прочие значения параметра не удовлетворяют условию.
одна из ветвей графика модуля не пересекается с графиком второго уравнения, а другая ветвь имеет с ним не больше двух точек пересечения, поэтому прочие значения параметра не удовлетворяют условию.

 получают сдвигом графика функции
получают сдвигом графика функции 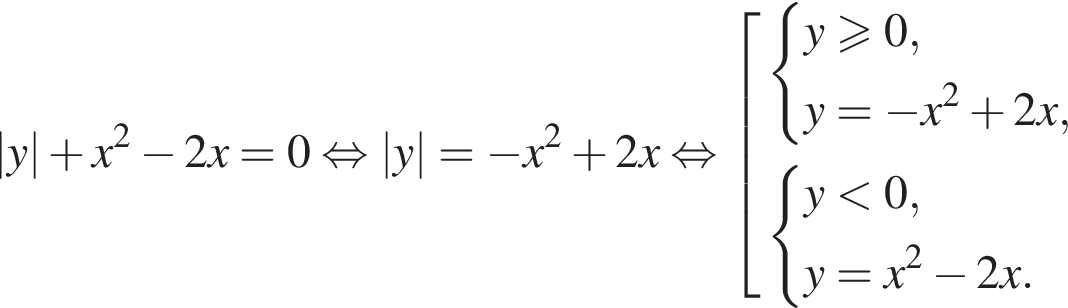




 и
и  построенных на отрезке [0; 2].
построенных на отрезке [0; 2].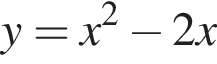 касается левой и правой ветвей графика функции
касается левой и правой ветвей графика функции  то есть прямых
то есть прямых  и
и  соответственно. Найдем
соответственно. Найдем 
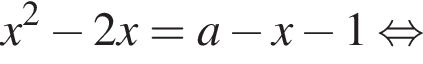

 Дискриминант обращается в нуль при
Дискриминант обращается в нуль при  При этом абсцисса точки касания
При этом абсцисса точки касания  удовлетворяет условию
удовлетворяет условию 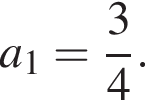 Аналогично найдем
Аналогично найдем 
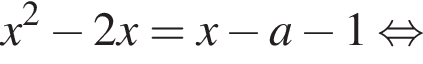

 он обращается в нуль при
он обращается в нуль при  При этом абсцисса точки касания
При этом абсцисса точки касания 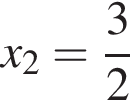 удовлетворяет условию
удовлетворяет условию 
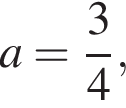

 и
и  графики пересекаются в ровно в четырех точках. При
графики пересекаются в ровно в четырех точках. При 

 представляет собой график функции
представляет собой график функции  сдвинутый на
сдвинутый на 
 является касательной к параболе
является касательной к параболе 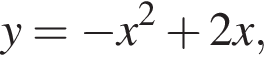 а прямая
а прямая  — касательной к параболе
— касательной к параболе 



 что противоречит второму уравнению системы. При
что противоречит второму уравнению системы. При 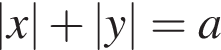 задает на координатной плоскости квадрат с вершинами на координатных осях и диагоналями, равными 2a. График второго уравнения получается из графика функции
задает на координатной плоскости квадрат с вершинами на координатных осях и диагоналями, равными 2a. График второго уравнения получается из графика функции  сдвигом на четыре единицы влево вдоль оси абсцисс.
сдвигом на четыре единицы влево вдоль оси абсцисс. имеет единственное решение. Имеем:
имеет единственное решение. Имеем:



 имеет единственное решение в том случае, если дискриминант равен нулю. Решим уравнение
имеет единственное решение в том случае, если дискриминант равен нулю. Решим уравнение 


 имеет единственное решение в том случае, если дискриминант равен нулю. Решим уравнение
имеет единственное решение в том случае, если дискриминант равен нулю. Решим уравнение 


 и
и  касаются при
касаются при  При найденном значении а абсциссой точки касания является
При найденном значении а абсциссой точки касания является  эта точка действительно лежит на стороне квадрата. Следовательно, система уравнений имеет два решения при
эта точка действительно лежит на стороне квадрата. Следовательно, система уравнений имеет два решения при  и
и 


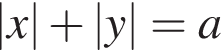 при
при  имеет единственное решение. Имеем:
имеет единственное решение. Имеем:



 имеет единственное решение в том случае, если дискриминант равен нулю. Решим уравнение D = 0:
имеет единственное решение в том случае, если дискриминант равен нулю. Решим уравнение D = 0:


 имеет единственное решение в том случае, если дискриминант равен нулю. Решим уравнение D = 0:
имеет единственное решение в том случае, если дискриминант равен нулю. Решим уравнение D = 0:


 и
и  касаются при a = 9,25. При найденном значении а абсциссой точки касания является
касаются при a = 9,25. При найденном значении а абсциссой точки касания является  эта точка действительно лежит на стороне квадрата. Следовательно, система уравнений имеет два решения при
эта точка действительно лежит на стороне квадрата. Следовательно, система уравнений имеет два решения при  и a = 9,25.
и a = 9,25.


 получаем, что каждому значению x, удовлетворяющему системе, соответствует ровно одно значение y. Поэтому количество решений системы совпадает с количеством корней уравнения
получаем, что каждому значению x, удовлетворяющему системе, соответствует ровно одно значение y. Поэтому количество решений системы совпадает с количеством корней уравнения  Рассмотрим два случая раскрытия модуля.
Рассмотрим два случая раскрытия модуля. то
то 
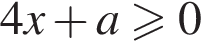 принимает вид
принимает вид


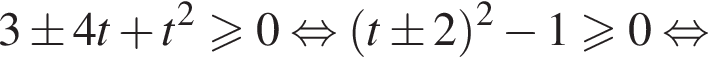









 раскрывая модуль, получаем уравнение
раскрывая модуль, получаем уравнение  решениями которого являются
решениями которого являются  Для найденных решений неравенство
Для найденных решений неравенство  принимает вид
принимает вид





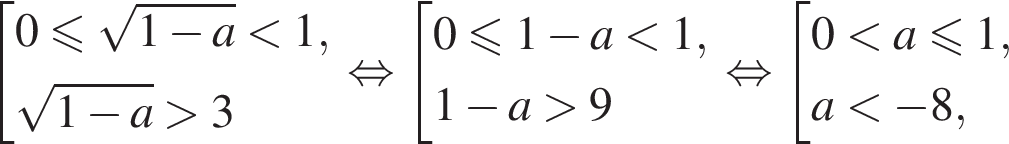


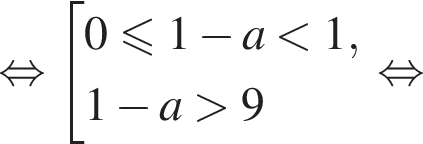


 два решения — случаи 2а) и 2б).
два решения — случаи 2а) и 2б). по два решения из каждого пункта, итого четыре решения.
по два решения из каждого пункта, итого четыре решения. два решения — случаи 1а) и 2б).
два решения — случаи 1а) и 2б). по два решения из каждого пункта, итого четыре решения.
по два решения из каждого пункта, итого четыре решения.


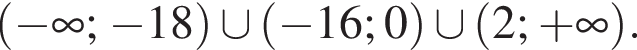


 Второе — часть гиперболы
Второе — часть гиперболы  при
при  если
если  Ясно, что при
Ясно, что при  тогда
тогда
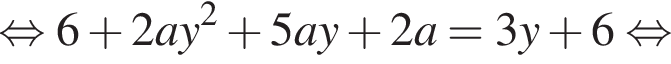



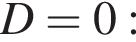



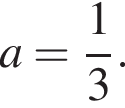 Теперь из геометрических соображений получаем, что при
Теперь из геометрических соображений получаем, что при  решений системы не меньше двух. Если же
решений системы не меньше двух. Если же  то решение ровно одно. В итоге получаем ответ:
то решение ровно одно. В итоге получаем ответ: 

 получают сдвигом графика функции
получают сдвигом графика функции  на 1 единицу вверх вдоль оси Oy и на |a| единиц вдоль оси Ox. Второе уравнение системы запишем в виде
на 1 единицу вверх вдоль оси Oy и на |a| единиц вдоль оси Ox. Второе уравнение системы запишем в виде 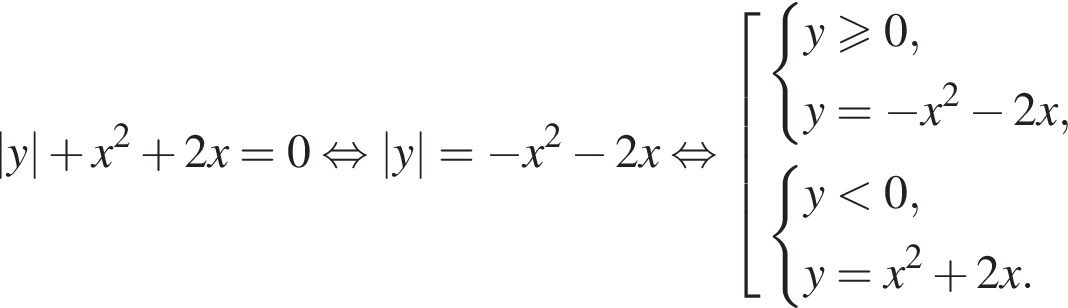




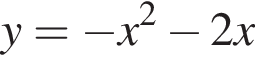 и
и 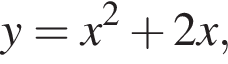 построенных на отрезке [−2; 0].
построенных на отрезке [−2; 0]. то есть прямых
то есть прямых  и
и  соответственно. Найдем
соответственно. Найдем 
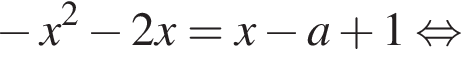

 он обращается в нуль при
он обращается в нуль при  При этом абсцисса точки касания
При этом абсцисса точки касания  удовлетворяет условию
удовлетворяет условию 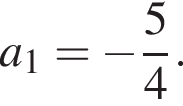 Аналогично найдем
Аналогично найдем 


 Дискриминант обращается в нуль при
Дискриминант обращается в нуль при  При этом абсцисса точки касания
При этом абсцисса точки касания  удовлетворяет условию
удовлетворяет условию 

 изображены зеленым и красным цветом).
изображены зеленым и красным цветом).
 и
и  графики пересекаются в ровно в четырех точках. При
графики пересекаются в ровно в четырех точках. При  и при
и при  одна из ветвей графика модуля не пересекается с графиком второго уравнения, а другая ветвь имеет с ним не больше двух точек пересечения, поэтому прочие значения параметра не удовлетворяют условию.
одна из ветвей графика модуля не пересекается с графиком второго уравнения, а другая ветвь имеет с ним не больше двух точек пересечения, поэтому прочие значения параметра не удовлетворяют условию.
 и/или
и/или 
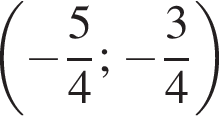 множества значений a, возможно, с включением граничных точек
множества значений a, возможно, с включением граничных точек 






 заключаем, что каждое из полученных в левой части уравнения слагаемых неотрицательно, поэтому их сумма равна нулю тогда и только тогда, когда каждое из них равно нулю:
заключаем, что каждое из полученных в левой части уравнения слагаемых неотрицательно, поэтому их сумма равна нулю тогда и только тогда, когда каждое из них равно нулю:

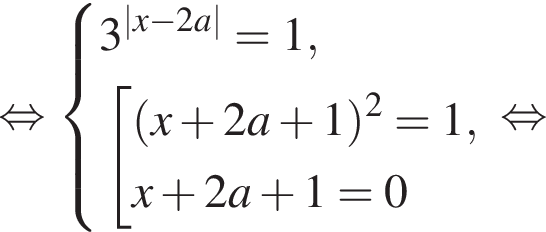





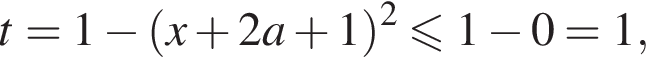 значит,
значит,  значит,
значит, 



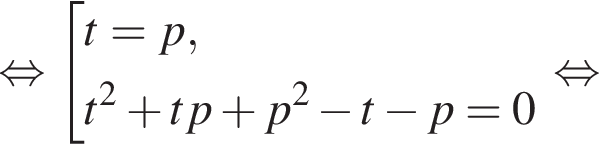



 откуда
откуда 
 Найдем дискриминант:
Найдем дискриминант: 


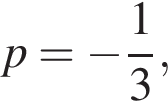 что невозможно ни при каких p или при
что невозможно ни при каких p или при  (см. первое уравнение совокупности).
(см. первое уравнение совокупности). Подставим
Подставим 

 тогда
тогда 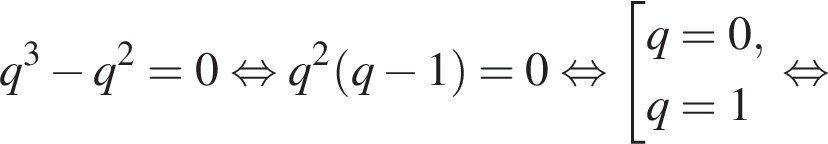









 или
или  и получена хотя бы одна из точек
и получена хотя бы одна из точек  и множества значений
и множества значений  и
и 
 множества значений a.
множества значений a.


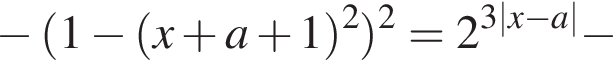



 поэтому правая часть равенства неотрицательна при всех значениях переменной. Левая часть уравнение неположительна, значит, равенство достигается тогда и только тогда, когда обе части равны нулю:
поэтому правая часть равенства неотрицательна при всех значениях переменной. Левая часть уравнение неположительна, значит, равенство достигается тогда и только тогда, когда обе части равны нулю:

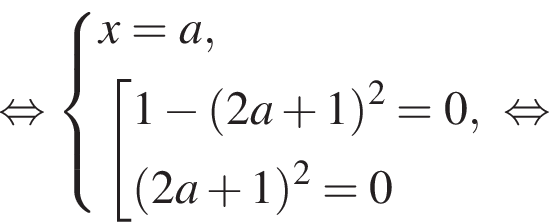

 При прочих значениях параметра уравнение решений не имеет.
При прочих значениях параметра уравнение решений не имеет.

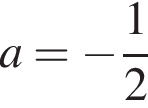 или
или  и получена хотя бы одна из точек
и получена хотя бы одна из точек 
 и
и 
 множества значений a.
множества значений a.



 тогда уравнение можно записать в виде
тогда уравнение можно записать в виде
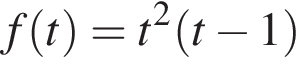 не принимает положительных значений. При
не принимает положительных значений. При  а тогда уравнение (⁎) равносильно уравнению
а тогда уравнение (⁎) равносильно уравнению 

 тогда уравнение (⁎⁎), а вместе с ним и исходное уравнение имеют хотя бы один корень тогда и только тогда, когда хотя бы один неотрицательный корень имеет уравнение
тогда уравнение (⁎⁎), а вместе с ним и исходное уравнение имеют хотя бы один корень тогда и только тогда, когда хотя бы один неотрицательный корень имеет уравнение
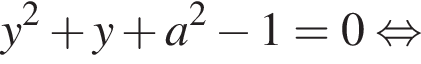

 Окружность пересекает вертикальную ось в точках −1 и 1 (см. рис.), уравнение имеет хотя бы одно неотрицательное решение, если
Окружность пересекает вертикальную ось в точках −1 и 1 (см. рис.), уравнение имеет хотя бы одно неотрицательное решение, если 

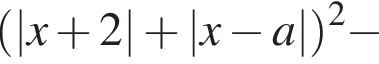



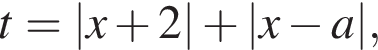 тогда исходное уравнение принимает вид:
тогда исходное уравнение принимает вид:

 или
или  Исследуем сколько решений имеет уравнение
Исследуем сколько решений имеет уравнение  в зависимости от a и
в зависимости от a и 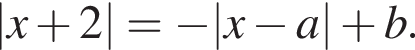 График левой части этого уравнения — график модуля с вершиной в точке
График левой части этого уравнения — график модуля с вершиной в точке  график правой части — график модуля, отражённый относительно
график правой части — график модуля, отражённый относительно  лежит правее (выше) прямой
лежит правее (выше) прямой  и прямая
и прямая  лежит левее (выше) прямой
лежит левее (выше) прямой  Это достигается условиями
Это достигается условиями  и
и  Таким образом, уравнение совокупности имеет два решения при условии:
Таким образом, уравнение совокупности имеет два решения при условии:
 то уравнение имеет два решения, если прямые
то уравнение имеет два решения, если прямые  и
и  или
или  или
или 

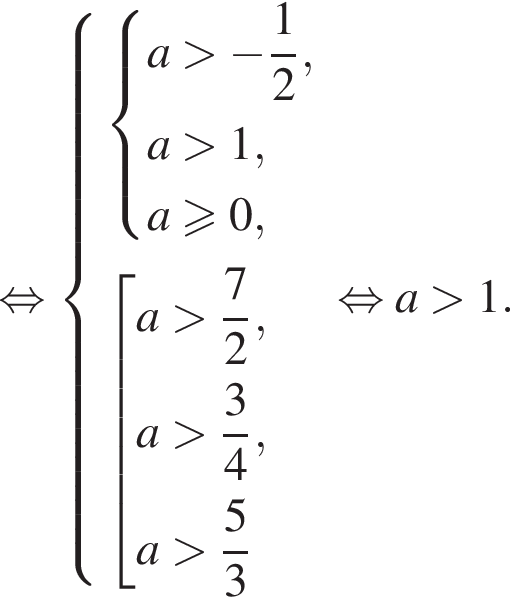
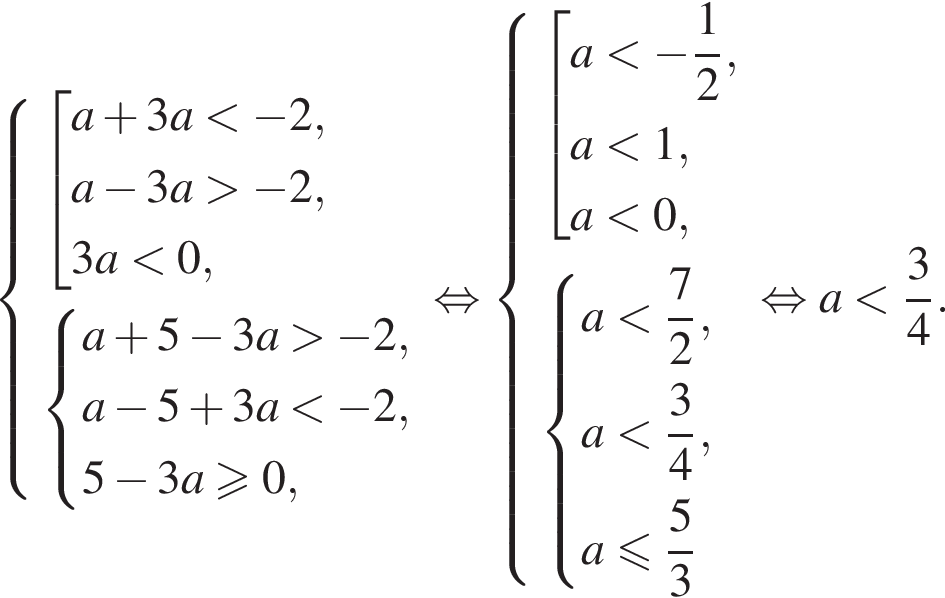


 откуда
откуда  При данном значении a оба уравнения принимают вид:
При данном значении a оба уравнения принимают вид: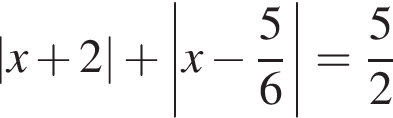

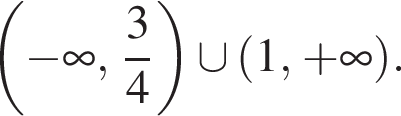


 и
и  и
и 
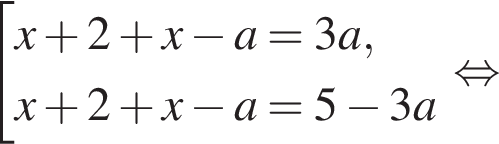

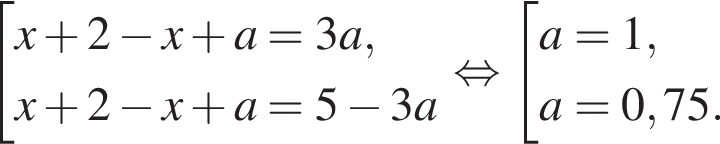
 и
и 
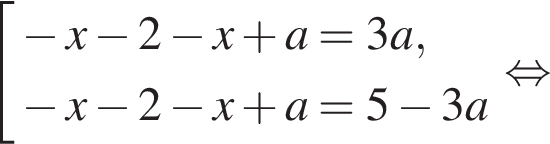


 или
или  или
или  исходное уравнение не имеет решений.
исходное уравнение не имеет решений.
 .
.