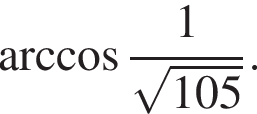В кубе ABCDA1B1C1D1
а) Докажите, что плоскость BA1C1 и прямая ![]() перпендикулярны.
перпендикулярны.
б) Найдите косинус угла между плоскостями BA1C1 и BA1D1.
Решение. а) Заметим, что проекция прямой
![]() на плоскость
на плоскость ![]() это прямая
это прямая ![]() Проекция прямой
Проекция прямой ![]() на плоскость
на плоскость ![]() это прямая
это прямая ![]()
 и
и  как диагонали квадрата. Таким образом, по теореме о трех перпендикулярах
как диагонали квадрата. Таким образом, по теореме о трех перпендикулярах  и
и  Тогда, по признаку перпендикулярности прямой и плоскости,
Тогда, по признаку перпендикулярности прямой и плоскости, 
б) Пусть точка O — центр куба, а M — середина ![]()
 а MO — средняя линия треугольника
а MO — средняя линия треугольника  поэтому
поэтому  Треугольник
Треугольник ![]() — равносторонний,
— равносторонний,  следовательно, искомый угол равен углу
следовательно, искомый угол равен углу 
Примем длины ребер куба за ![]() Найдем стороны треугольника
Найдем стороны треугольника  Из треугольника
Из треугольника  находим
находим  из равностороннего треугольника
из равностороннего треугольника ![]() находим
находим

Поскольку O — середина диагонали ![]() то
то  Теперь применим к треугольнику
Теперь применим к треугольнику ![]() теорему косинусов:
теорему косинусов:









Ответ: ![]()
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) ИЛИ имеется верное доказательство утверждения пункта а), и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а), ИЛИ при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | 1 |
| Решение не соответствует ни одному из критериев, приведённых выше | 0 |
| Максимальный балл | 3 |





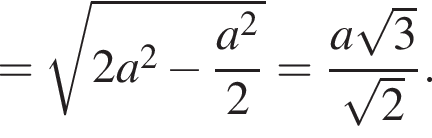




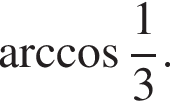















 откуда
откуда 




 и
и  диагонали перпендикулярны, поэтому
диагонали перпендикулярны, поэтому  Кроме того,
Кроме того,  так как BC перпендикулярна плоскости
так как BC перпендикулярна плоскости 
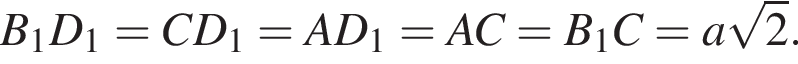 Опустим перпендикуляры
Опустим перпендикуляры 






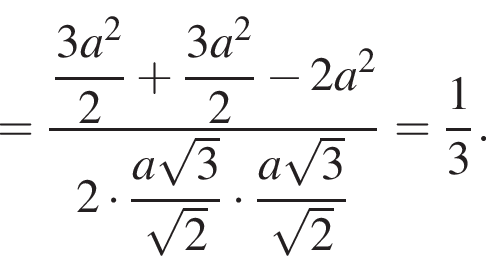





 параллельны.
параллельны. Значит, по признаку параллельности плоскостей,
Значит, по признаку параллельности плоскостей, 
 и
и  значит, угол DEA — линейный угол искомого угла. Из прямоугольного треугольника DAE находим
значит, угол DEA — линейный угол искомого угла. Из прямоугольного треугольника DAE находим 
 по теореме о трех перпендикулярах. Следовательно, высоты треугольников ABD и A1BD имеют общее основание H.
по теореме о трех перпендикулярах. Следовательно, высоты треугольников ABD и A1BD имеют общее основание H.






 и
и  (так как
(так как  ), имеем
), имеем  Поскольку плоскости ABC и
Поскольку плоскости ABC и 

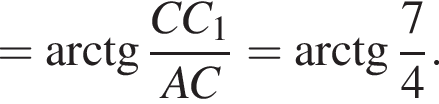

 (свойство диагоналей правильного шестиугольника) и
(свойство диагоналей правильного шестиугольника) и  (поскольку верхнее основание призмы перпеникулярно боковому ребру), то
(поскольку верхнее основание призмы перпеникулярно боковому ребру), то  а тогда и
а тогда и  (признак перпендикулярности плоскостей).
(признак перпендикулярности плоскостей). откуда
откуда  Кроме того
Кроме того  поскольку
поскольку  Тогда
Тогда






 то и
то и  Аналогично
Аналогично  (надо рассмотреть плоскость
(надо рассмотреть плоскость 


 откуда
откуда а угол между плоскостями —
а угол между плоскостями — 

 Отсюда отрезки
Отсюда отрезки  Из точки D проведём перпендикуляр
Из точки D проведём перпендикуляр  Плоский угол
Плоский угол  следовательно,
следовательно,
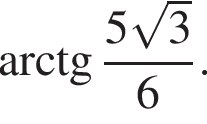
 а боковое ребро AA1 = 5.
а боковое ребро AA1 = 5.
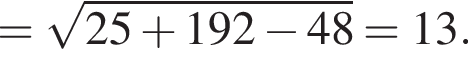


 (потому что его проекция на основание
(потому что его проекция на основание  (потому что
(потому что 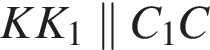 ), то
), то 


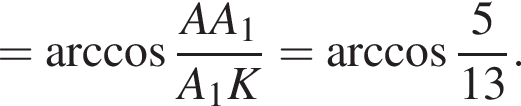




 а боковое ребро AA1 = 8.
а боковое ребро AA1 = 8. (так как
(так как  ) Значит,
) Значит,  Итак, плоскость
Итак, плоскость  поэтому плоскости перпендикулярны.
поэтому плоскости перпендикулярны. (так как
(так как  ) и
) и  по теореме о трех перпендикулярах (проекция
по теореме о трех перпендикулярах (проекция  ) Поэтому
) Поэтому







 вершина S проектируется в точку пересечения диагоналей, поэтому боковые ребра равны между собой. По теореме косинусов в треугольнике ABS:
вершина S проектируется в точку пересечения диагоналей, поэтому боковые ребра равны между собой. По теореме косинусов в треугольнике ABS:


 тогда
тогда  откуда
откуда  Аналогично находим
Аналогично находим  Тогда:
Тогда:
 что и требовалось доказать.
что и требовалось доказать.


 В треугольнике CBQ: угол Q — прямой,
В треугольнике CBQ: угол Q — прямой,  тогда
тогда  В треугольнике APB: угол P — прямой,
В треугольнике APB: угол P — прямой,  В треугольнике ABC': угол B — прямой,
В треугольнике ABC': угол B — прямой, 




 как показано на рисунке. По правилам сложения векторов получаем:
как показано на рисунке. По правилам сложения векторов получаем:  Запишем условие перпендикулярности:
Запишем условие перпендикулярности: 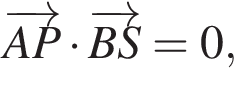 откуда ##
откуда ##
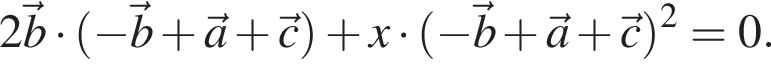




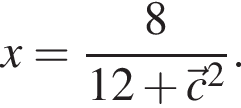
 и
и  Значит,
Значит,  Применим выражения векторов через базис и упростим получившиеся уравнение так же, как это сделано выше. В результате получаем:
Применим выражения векторов через базис и упростим получившиеся уравнение так же, как это сделано выше. В результате получаем: 

 Сравнивая коэффициенты, находим, что
Сравнивая коэффициенты, находим, что  Следовательно, точка P делит пополам отрезок BQ, что и требовалось доказать.
Следовательно, точка P делит пополам отрезок BQ, что и требовалось доказать. Теперь воспользуемся выражениями векторов, которые из п. а), откуда получим:
Теперь воспользуемся выражениями векторов, которые из п. а), откуда получим: 
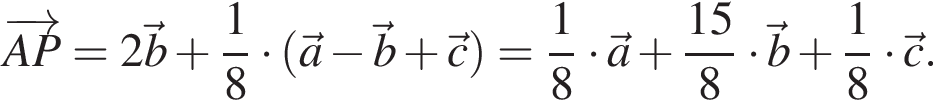










 и
и  Основания этих пирамид − равные прямоугольные трапеции, а высоты равны высоте равностороннего треугольника ABC, поэтому они тоже равны. Следовательно, равны и объемы этих пирамид. Что и требовалось доказать.
Основания этих пирамид − равные прямоугольные трапеции, а высоты равны высоте равностороннего треугольника ABC, поэтому они тоже равны. Следовательно, равны и объемы этих пирамид. Что и требовалось доказать.

 и KCD получаем:
и KCD получаем: 
 высота CH является высотой и биссектрисой, откуда
высота CH является высотой и биссектрисой, откуда 
 тогда
тогда 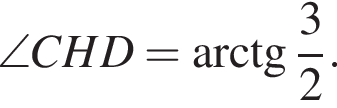

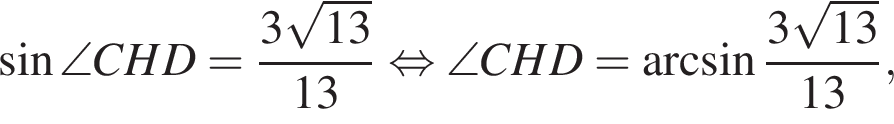

 треугольник ABC — прямоугольный. Введем координаты с началом в точке C и с осями x, y, z, направленными вдоль ребер CA, CB, CC1 соответственно. Тогда координаты точек будут
треугольник ABC — прямоугольный. Введем координаты с началом в точке C и с осями x, y, z, направленными вдоль ребер CA, CB, CC1 соответственно. Тогда координаты точек будут
 уравнение плоскости A1B1C будет
уравнение плоскости A1B1C будет  Тогда, если α искомый угол, то
Тогда, если α искомый угол, то 

 Аналогично доказывается, что
Аналогично доказывается, что 
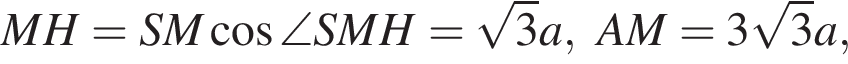



 Значит,
Значит, 
 и
и  Искомый угол между боковыми гранями равен углу при вершине равнобедренного треугольника
Искомый угол между боковыми гранями равен углу при вершине равнобедренного треугольника 






 следовательно,
следовательно,  Теперь вычислим
Теперь вычислим 
 следовательно, QB = 4PB и
следовательно, QB = 4PB и  и
и 


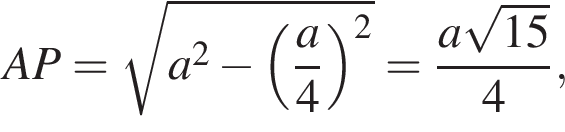






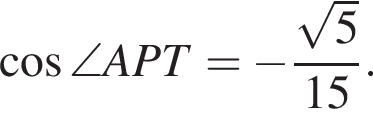 Таким образом,
Таким образом, 

 BC = 6. Высота пирамиды проходит через точку пересечения диагоналей прямоугольника. Из вершин A и C опущены перпендикуляры AP и CQ на ребро SB.
BC = 6. Высота пирамиды проходит через точку пересечения диагоналей прямоугольника. Из вершин A и C опущены перпендикуляры AP и CQ на ребро SB. 





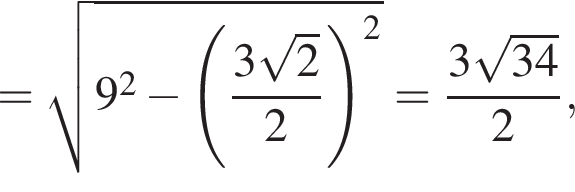



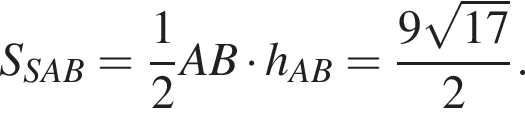










 по доказанному ранее,
по доказанному ранее, 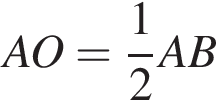 = 15. Тогда по теореме Пифагора
= 15. Тогда по теореме Пифагора  Наконец,
Наконец,  а
а 






 Высота пирамиды проектируется в точку пересечения диагоналей основания. Из вершин A и C на ребро SB опущены перпендикуляры AP и CQ.
Высота пирамиды проектируется в точку пересечения диагоналей основания. Из вершин A и C на ребро SB опущены перпендикуляры AP и CQ.

 и
и  Таким образом,
Таким образом,  следовательно, точка P — середина отрезка BQ.
следовательно, точка P — середина отрезка BQ.









 Высота пирамиды проецируется в точку пересечения диагоналей основания. Из вершин А и C на ребро SB опущены перпендикуляры AP и CQ.
Высота пирамиды проецируется в точку пересечения диагоналей основания. Из вершин А и C на ребро SB опущены перпендикуляры AP и CQ.