1. Тип Д11 C3 № 484598 

Классификатор алгебры: Системы неравенств
Кодификатор ФИПИ/Решу ЕГЭ: 2.2.3 Показательные неравенства
Простые системы неравенств. Рациональные, иррациональные, показательные неравенства
i
Решите систему неравенств 
Решение. Последовательно получаем:












Ответ: 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 3 |
| Обоснованно получены верные ответы в обоих неравенствах системы неравенств | 2 |
| Обоснованно получен верный ответ в одном из неравенств системы неравенств | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ответ: 

484598

Классификатор алгебры: Системы неравенств
Кодификатор ФИПИ/Решу ЕГЭ: 2.2.3 Показательные неравенства


 или
или 
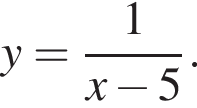 Получим:
Получим:

 получаем:
получаем:  или
или 







 или
или 
 Получим
Получим

 получаем
получаем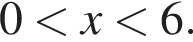
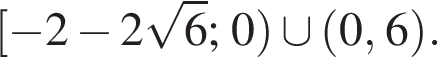
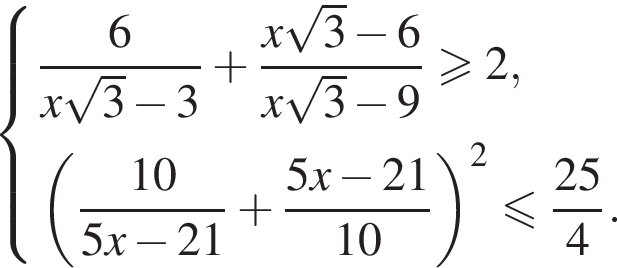
 получаем:
получаем: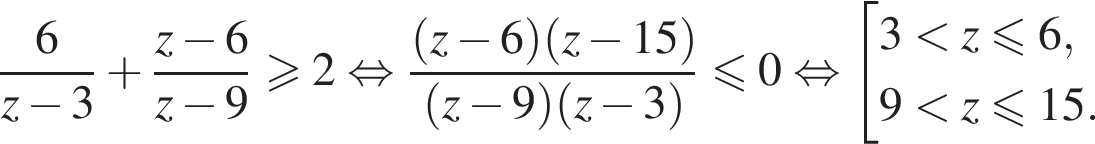




 или
или 
 получаем:
получаем:
 или
или 
 получаем решение системы:
получаем решение системы: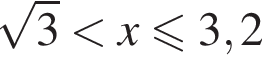 или
или 

 Решение: x = 2,8 или x ≤ 2,5.
Решение: x = 2,8 или x ≤ 2,5.



 и
и  Пересекая решения полученных неравенств получаем множество решений исходного неравенства:
Пересекая решения полученных неравенств получаем множество решений исходного неравенства: 

 Решение: x = 1,8 или x ≤ 1,5.
Решение: x = 1,8 или x ≤ 1,5.



 и
и 




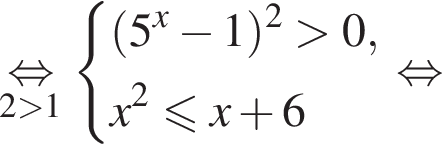







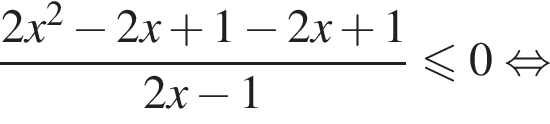






 получаем неравенство
получаем неравенство  откуда
откуда 
 откуда
откуда 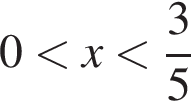 или
или 

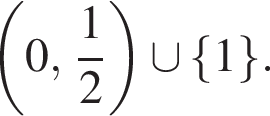







 Тогда
Тогда 
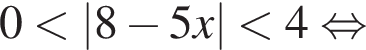




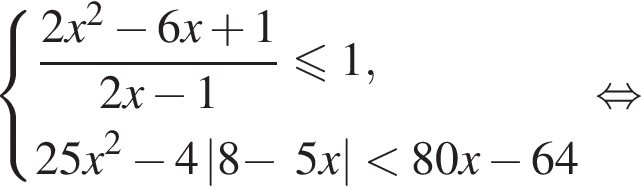






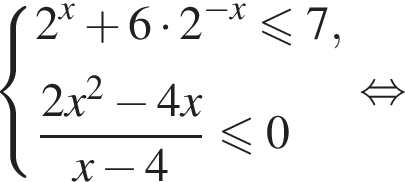










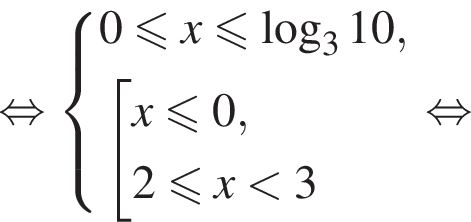
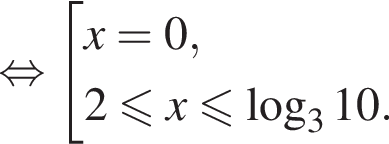









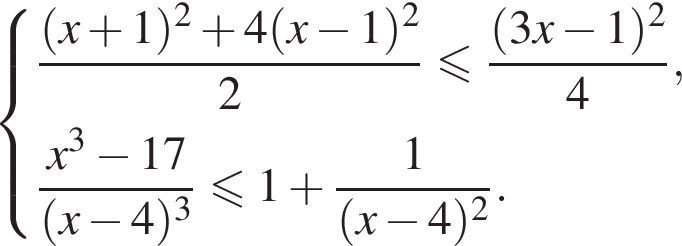

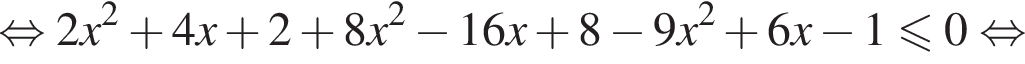



 — верное
— верное



 откуда
откуда  возвращаясь к исходной переменной получим:
возвращаясь к исходной переменной получим:


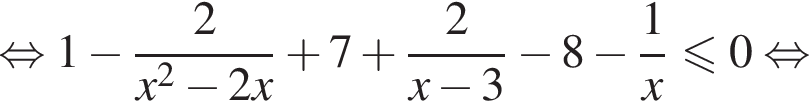





 множество решений исходной системы неравенств:
множество решений исходной системы неравенств: 




 откуда
откуда  возвращаясь к исходной переменной, получим:
возвращаясь к исходной переменной, получим:







 получаем множество решений исходной системы неравенств:
получаем множество решений исходной системы неравенств: 







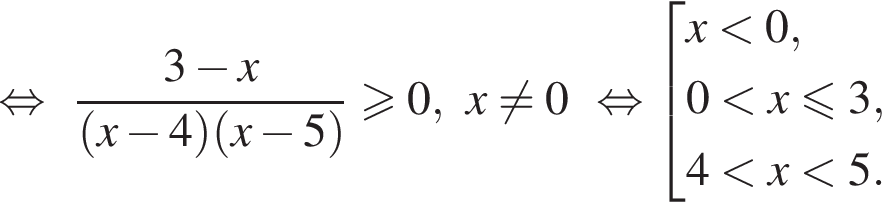


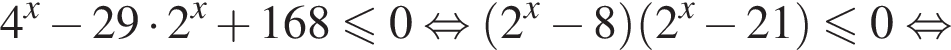




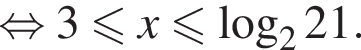



 Пусть
Пусть  откуда
откуда  возвращаясь к исходной переменной получаем:
возвращаясь к исходной переменной получаем:
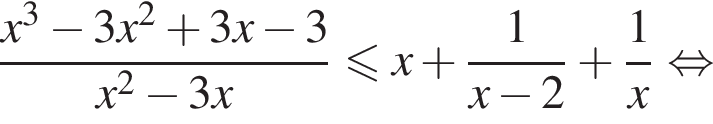



 получаем множество решений исходной системы неравенств:
получаем множество решений исходной системы неравенств:
 Пусть
Пусть 











 получаем:
получаем: 

 По теореме, обратной теореме Виета, сумма его корней равна
По теореме, обратной теореме Виета, сумма его корней равна  а их произведение равно
а их произведение равно  Поэтому это числа
Поэтому это числа 


 и
и  имеют одинаковые знаки; для любых для
имеют одинаковые знаки; для любых для  и
и  имеют одинаковые знаки.
имеют одинаковые знаки.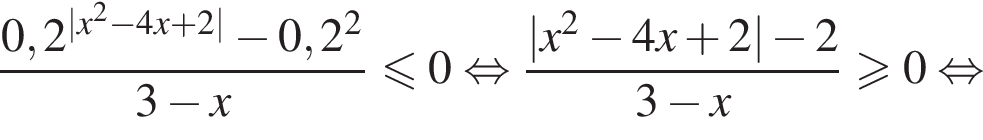
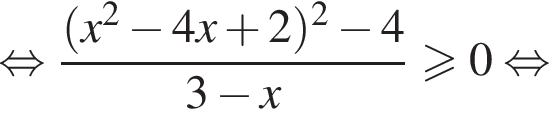
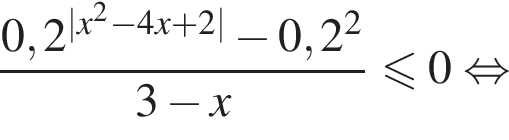

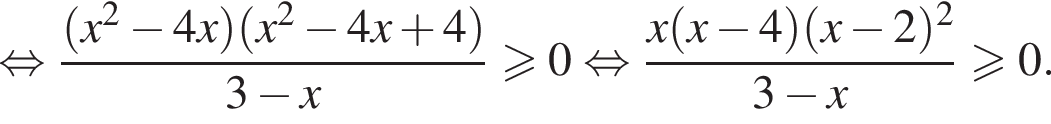


 или
или  получаем решение системы.
получаем решение системы.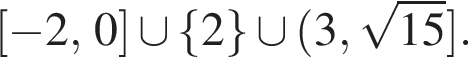









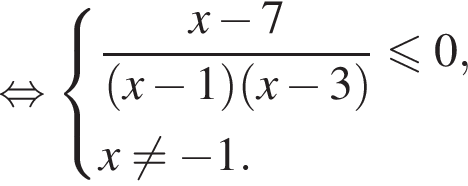

 получаем:
получаем: 




 откуда
откуда  возвращаясь к исходной переменной получаем:
возвращаясь к исходной переменной получаем:






 получаем что множество решений исходной системы:
получаем что множество решений исходной системы: 
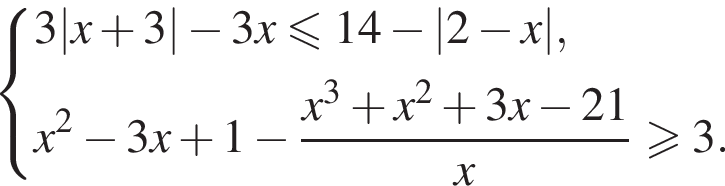
 возможны четыре случая раскрытия модулей, откуда заключаем:
возможны четыре случая раскрытия модулей, откуда заключаем:






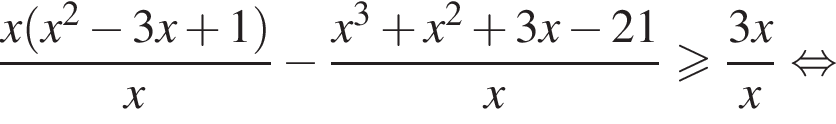
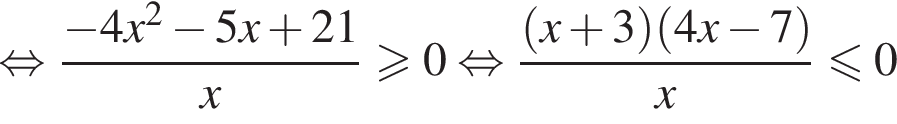



 или
или 
 или
или 








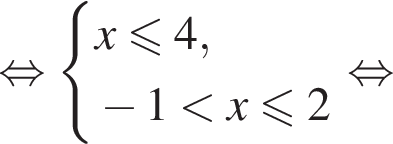

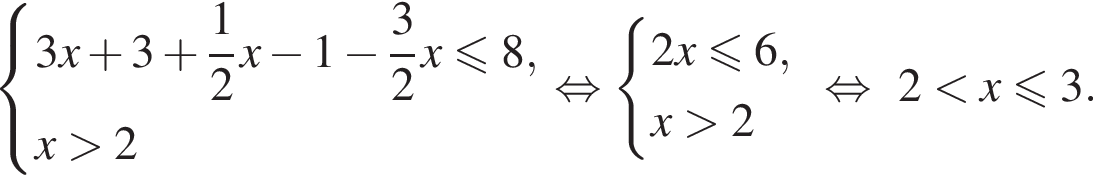













 получаем:
получаем:



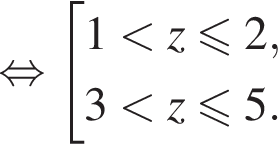
 или
или 
 получаем:
получаем:

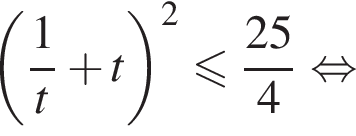



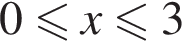 или
или 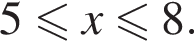
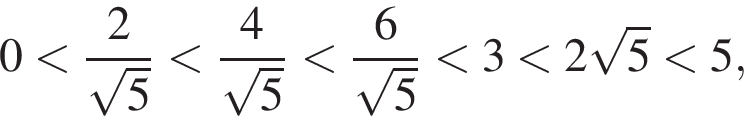 получаем множетсво решений системы:
получаем множетсво решений системы: 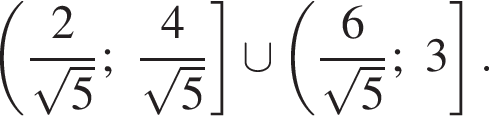

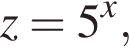 получаем:
получаем: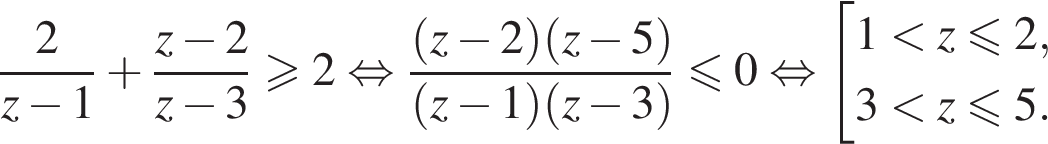

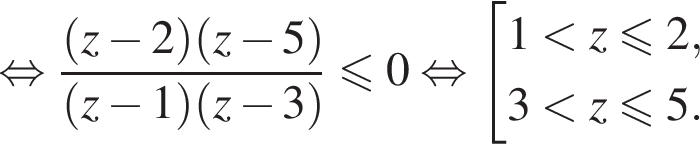


 или
или 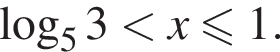
 получаем:
получаем: 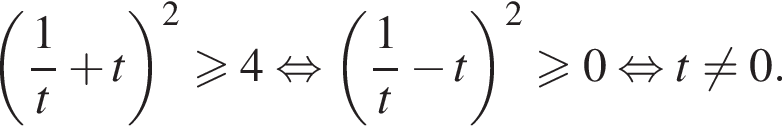
 и
и  Заметим, что
Заметим, что  а
а 
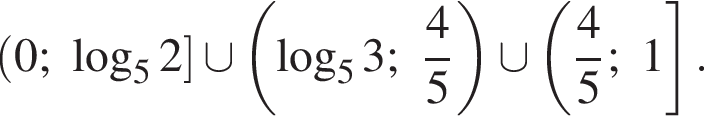

 При любом
При любом  не выполняется. При
не выполняется. При  решением которого с учетом условия
решением которого с учетом условия  и второе неравенство равносильно неравенству
и второе неравенство равносильно неравенству  Решим систему:
Решим систему:




 и точка
и точка 







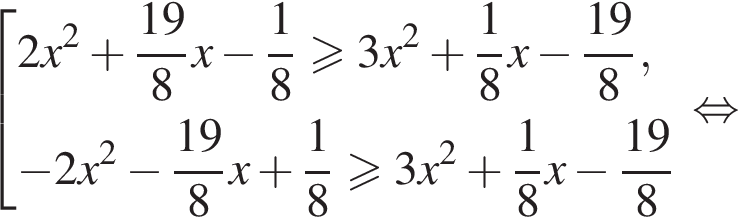





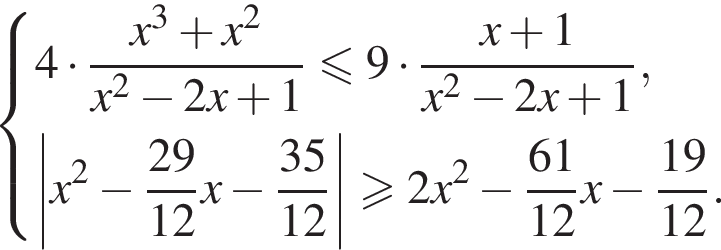


















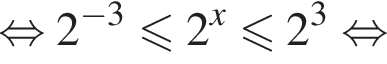

 решим второе неравенство, запомнив, что
решим второе неравенство, запомнив, что 


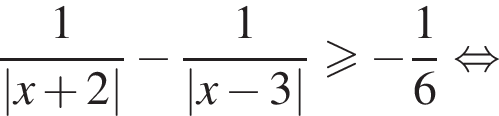

 правая часть неравенства неотрицательна, получаем систему:
правая часть неравенства неотрицательна, получаем систему:


















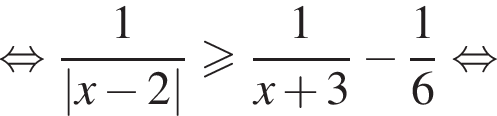







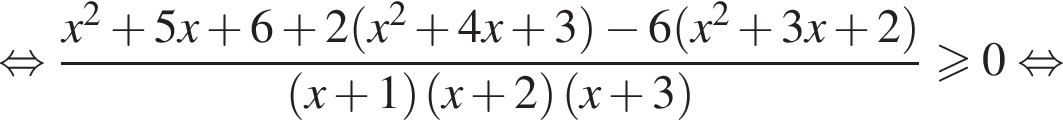




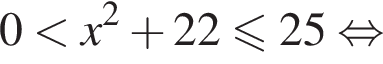

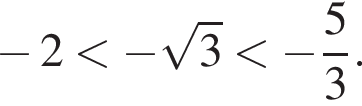 Таким образом, множество решений исходной системы неравенств:
Таким образом, множество решений исходной системы неравенств: 





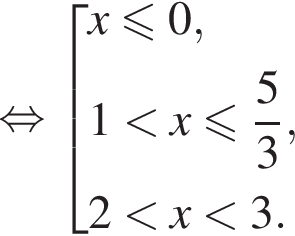

 Таким образом, множество решений исходной системы:
Таким образом, множество решений исходной системы: 





















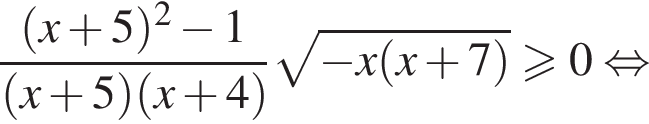

 то есть при
то есть при  :
: 



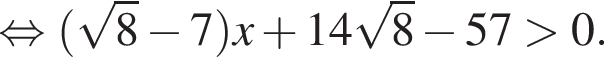
 тогда
тогда 

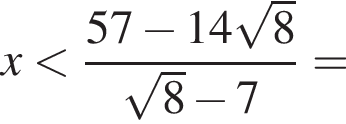


 получим множество решений исходной системы неравенств:
получим множество решений исходной системы неравенств: 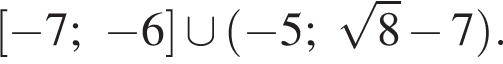



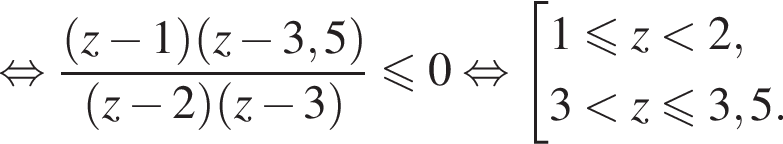

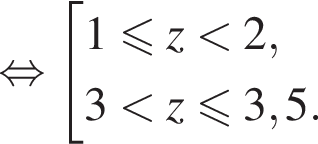
 или
или 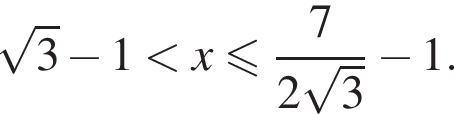


 выполнено при всех x, кроме всех
выполнено при всех x, кроме всех  и
и  причем
причем и
и 



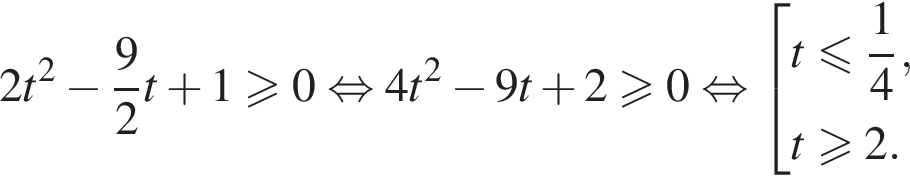





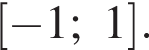


 получим
получим 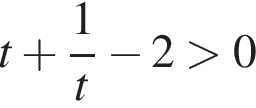 при всех положительных t, кроме
при всех положительных t, кроме  не влияет на знак, кроме как при
не влияет на знак, кроме как при  с ответом
с ответом 

