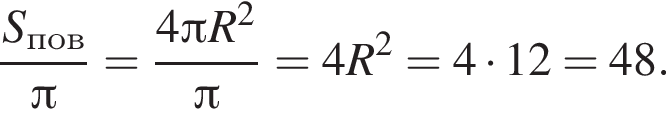1. Тип 3 № 5077 

Источник: ЕГЭ по математике 29.06.2021. Основная волна, резервный день. Центр. Вариант 401
Кодификатор ФИПИ/Решу ЕГЭ:
Стереометрия. Комбинации тел
i
Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шара.
Решение. Радиусы шара и основания цилиндра равны. Площадь поверхности цилиндра радиусом основания r и высотой 2r равна





Площадь поверхности шара радиуса r равна  она в
она в
Ответ: 12.
Ответ: 12
5077
12



 Поскольку гипотенуза является диаметром основания описанного цилиндра, его объем равен
Поскольку гипотенуза является диаметром основания описанного цилиндра, его объем равен
 является диаметром описанного вокруг призмы цилиндра. Тогда объем цилиндра равен
является диаметром описанного вокруг призмы цилиндра. Тогда объем цилиндра равен


 и поэтому он в
и поэтому он в 
 Тогда для объема конуса, деленного на
Тогда для объема конуса, деленного на 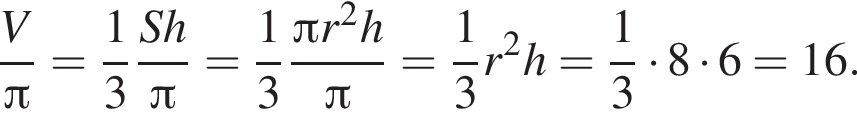


 Тогда объем шара равен
Тогда объем шара равен


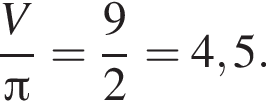
 с ребром 1,6 является центром сферы, проходящей через
с ребром 1,6 является центром сферы, проходящей через 






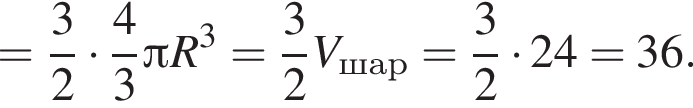
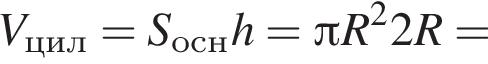
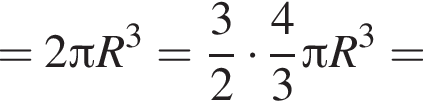
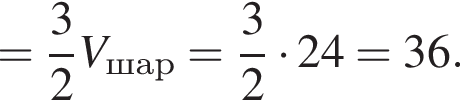











 Следовательно, ребро куба равно 2, а его объем равен 8.
Следовательно, ребро куба равно 2, а его объем равен 8. 


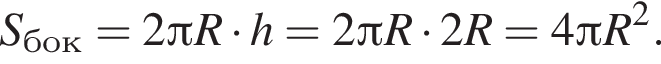



 имеем:
имеем: 
 Объём шара вычисляется по формуле
Объём шара вычисляется по формуле  откуда имеем:
откуда имеем: 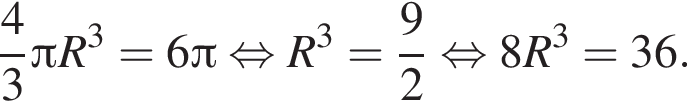
 откуда, учитывая, что
откуда, учитывая, что  или
или 
 откуда, учитывая, что
откуда, учитывая, что  или
или 
 Следовательно,
Следовательно,




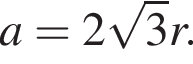 Тогда площадь боковой поверхности призмы выражается формулой
Тогда площадь боковой поверхности призмы выражается формулой 




 Площадь боковой поверхности призмы тогда равна
Площадь боковой поверхности призмы тогда равна 
 Тогда площадь боковой поверхности призмы выражается формулой
Тогда площадь боковой поверхности призмы выражается формулой 
 где r — радиус основания, h — высота, l — образующая. В силу соотношения
где r — радиус основания, h — высота, l — образующая. В силу соотношения  учитывая, что
учитывая, что 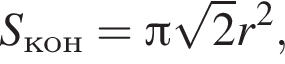 откуда находим квадрат радиуса:
откуда находим квадрат радиуса: 

 Объём шара вычисляется по формуле
Объём шара вычисляется по формуле 

 где a — сторона треугольника. Значит,
где a — сторона треугольника. Значит, 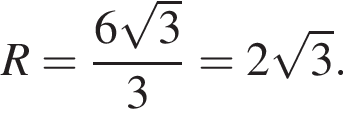 Итак,
Итак,