1. Тип 15 № 507691 

Классификатор алгебры: Неравенства с модулями, Неравенства смешанного типа
Методы алгебры: Метод интервалов
Кодификатор ФИПИ/Решу ЕГЭ:
Неравенства. Другие неравенства смешанного типа
i
Решите неравенство: 
Решение. Используя свойства логарифмов, преобразуем неравенство:


При ![]() :
:
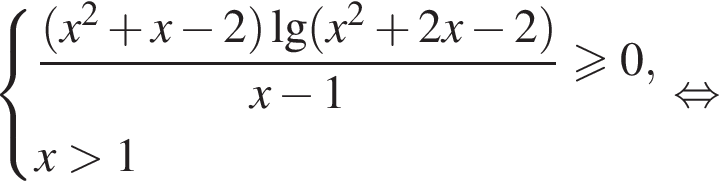
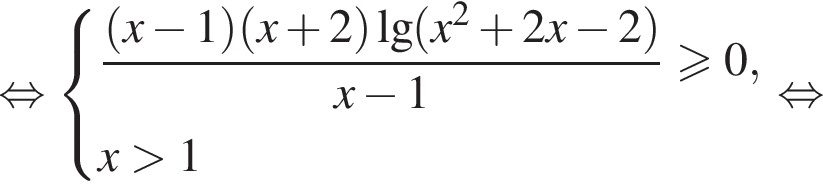





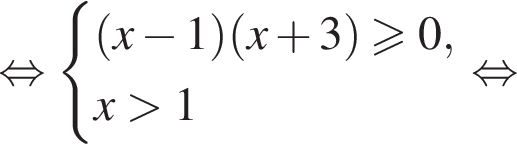

При ![]() :
:

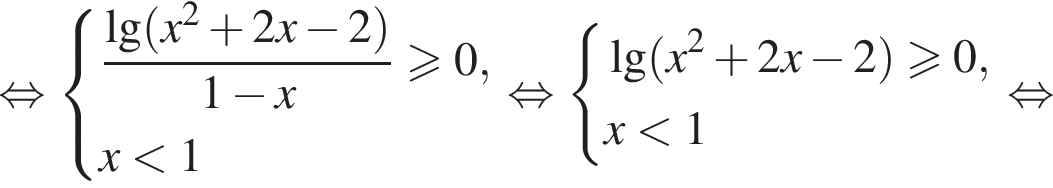












Таким образом, получаем, что решение неравенства — множество 
Ответ: 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 2 |
| Обоснованно получен ответ, отличающийся от верного исключением точек, ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Ответ: 

507691

Классификатор алгебры: Неравенства с модулями, Неравенства смешанного типа
Методы алгебры: Метод интервалов
Кодификатор ФИПИ/Решу ЕГЭ:




 тогда
тогда 
 :
:









 тогда
тогда 







 удовлетворяют условию
удовлетворяют условию  то есть неравенству
то есть неравенству 














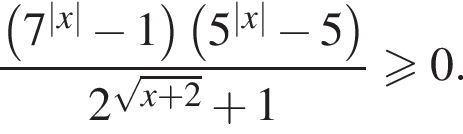
 при любом
при любом  при
при  неравенство решений не имеет.
неравенство решений не имеет.
 тогда
тогда  откуда
откуда 











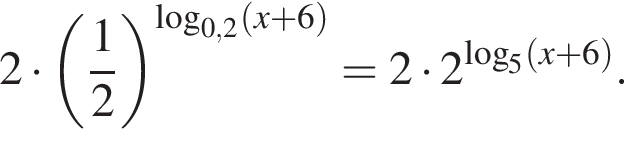











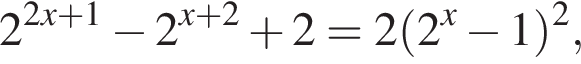 при условии
при условии 





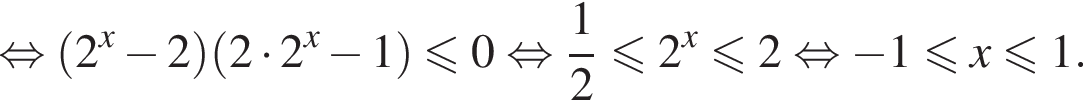




 представим первый множитель в числителе в виде
представим первый множитель в числителе в виде 




 имеет тот же знак, что и разность
имеет тот же знак, что и разность  и разность
и разность 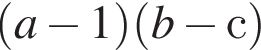 также имеют одинаковые знаки. Наконец, одинаковые знаки имеют выражения
также имеют одинаковые знаки. Наконец, одинаковые знаки имеют выражения  и
и  Последовательно заменяя множители в числителе выражениями того же знака и учитывая ОДЗ, получим равносильное неравенство:
Последовательно заменяя множители в числителе выражениями того же знака и учитывая ОДЗ, получим равносильное неравенство: 






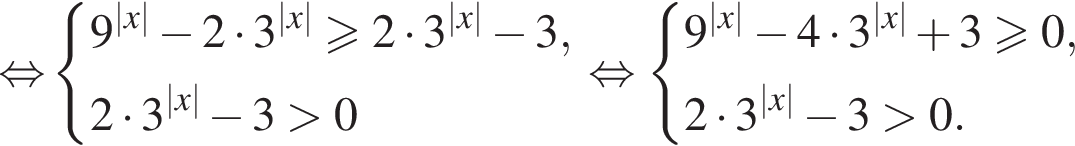


 тогда
тогда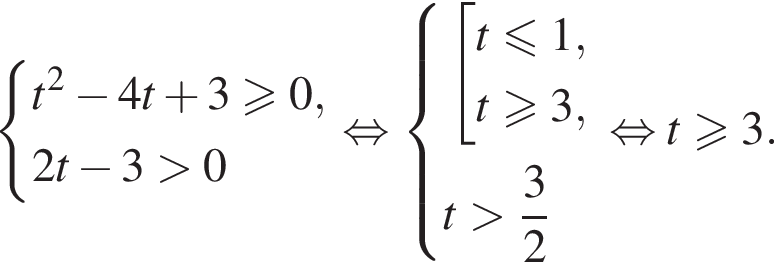










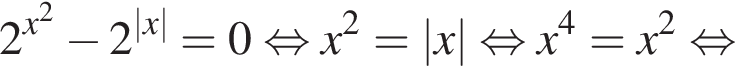












 то система равносильна неравенству
то система равносильна неравенству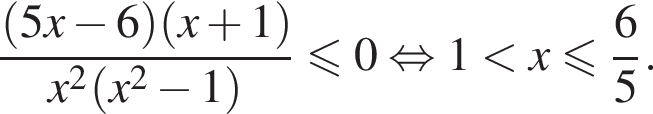







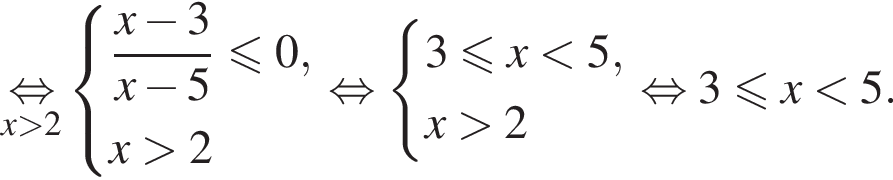



 и
и  определены при
определены при 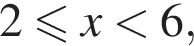 равны нулю в точках
равны нулю в точках  откуда
откуда  то есть
то есть  Полуинтервалу [2; 6) принадлежат решения
Полуинтервалу [2; 6) принадлежат решения  осталось присоединить в ним числа
осталось присоединить в ним числа 












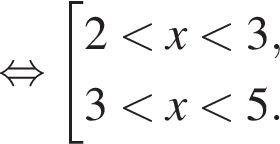



 выражение
выражение  определено и неравенство является верным.
определено и неравенство является верным. выражение
выражение  положительно и на него можно разделить, не меняя знак неравенства. Получаем:
положительно и на него можно разделить, не меняя знак неравенства. Получаем:






 получаем:
получаем:  или
или 






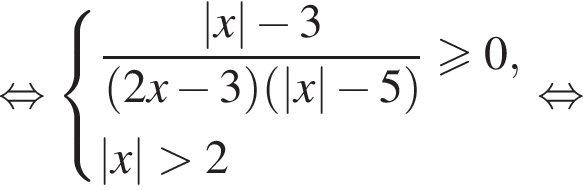

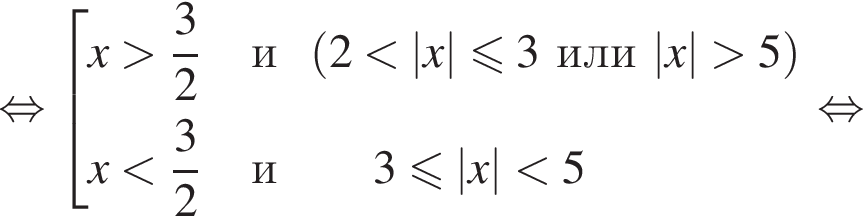



 :
:













 неравенство принимает вид
неравенство принимает вид 
 получаем:
получаем:


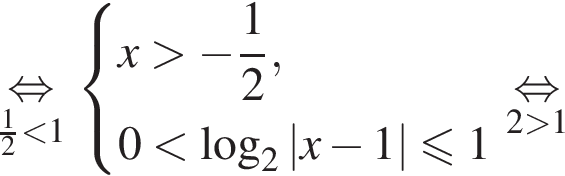






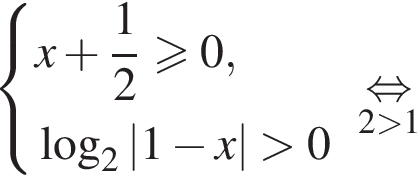


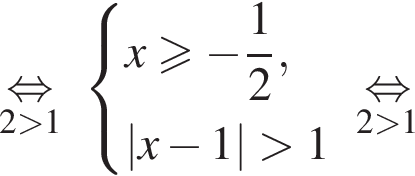











 а второй множитель обращается в нуль, если
а второй множитель обращается в нуль, если  откуда
откуда  (вне ОДЗ), или если
(вне ОДЗ), или если  неравенство сохраняет знак, а на открытом луче
неравенство сохраняет знак, а на открытом луче  может поменять знак в точке 3. Выясним знаки неравенства на этих промежутках, взяв на них пробные точки.
может поменять знак в точке 3. Выясним знаки неравенства на этих промежутках, взяв на них пробные точки. заметим, что
заметим, что  а потому
а потому  Таким образом, оба множителя в пробной точке, а значит, и на интервале
Таким образом, оба множителя в пробной точке, а значит, и на интервале  положительны.
положительны. заметим, что
заметим, что  а потому
а потому  Таким образом, оба множителя в пробной точке, а значит, и на интервале (2; 3) положительны.
Таким образом, оба множителя в пробной точке, а значит, и на интервале (2; 3) положительны. а
а  Таким образом, первый множитель в пробной точке, а значит, и на всем луче
Таким образом, первый множитель в пробной точке, а значит, и на всем луче  положителен, а второй — отрицателен.
положителен, а второй — отрицателен.

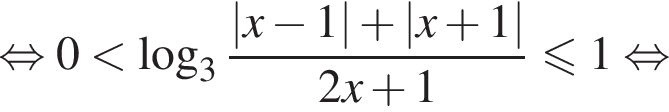
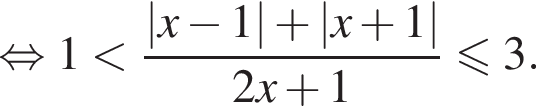

 имеем:
имеем:


 имеем:
имеем:




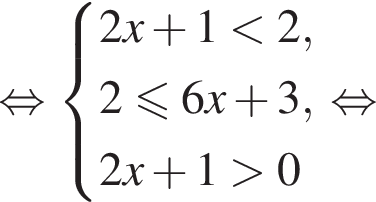




 тогда
тогда  Поэтому, умножив на положительный знаменатель и снимая модуль, получаем на луче
Поэтому, умножив на положительный знаменатель и снимая модуль, получаем на луче  :
:



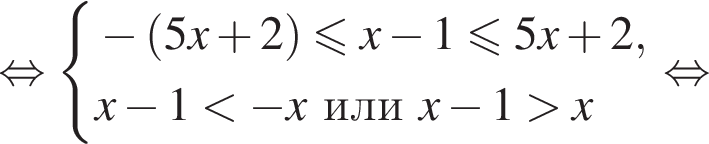



 Тогда
Тогда
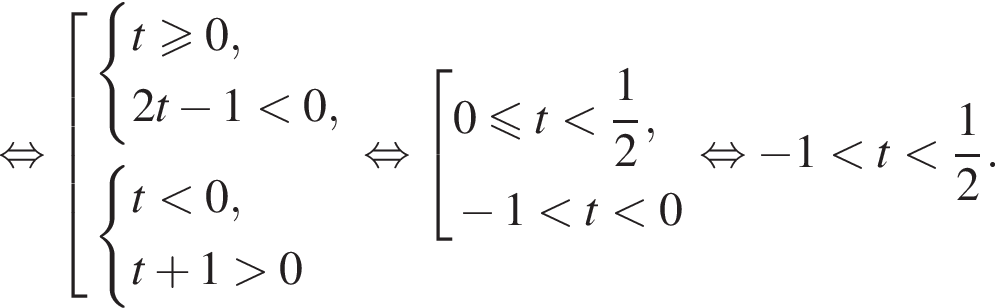










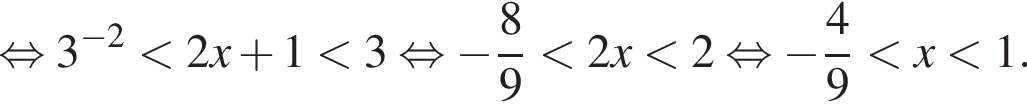



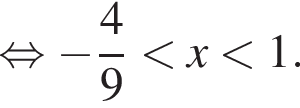
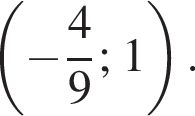


 или при
или при 





 или при
или при  получаем:
получаем:







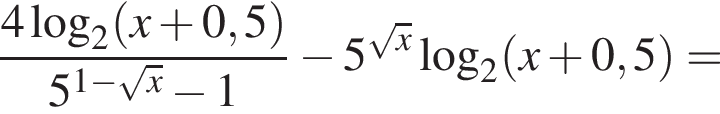




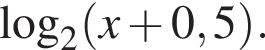 На области определения выражение
На области определения выражение 
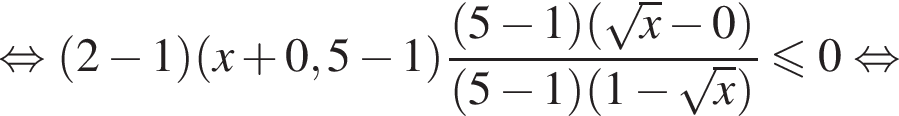

 или
или 





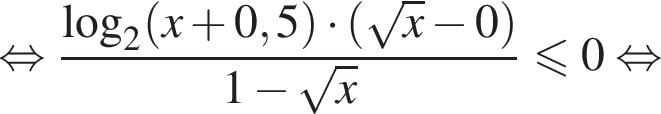







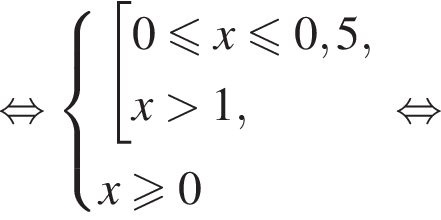





















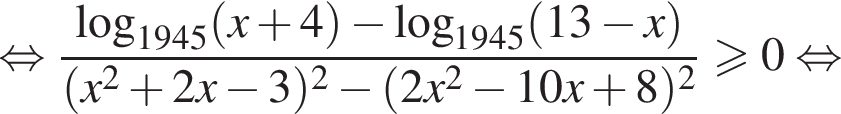
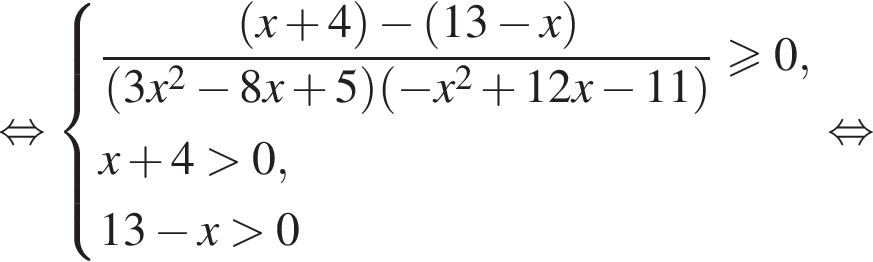










 получаем:
получаем: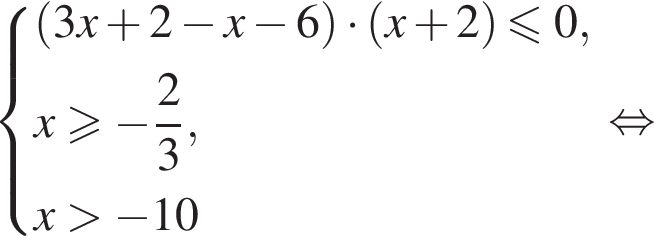



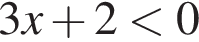 получаем:
получаем:
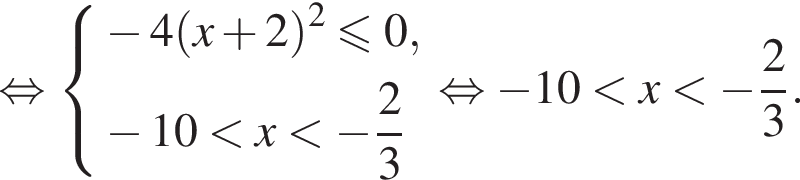





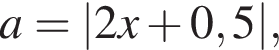
 перейдем к основанию 3 и разложим на множители:
перейдем к основанию 3 и разложим на множители:





 откуда получаем:
откуда получаем:










 тогда
тогда








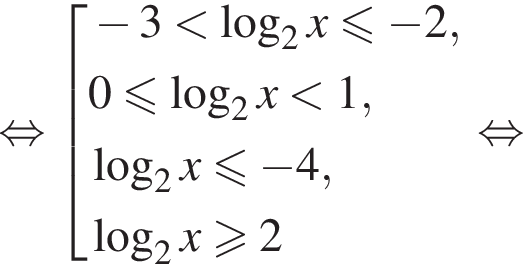
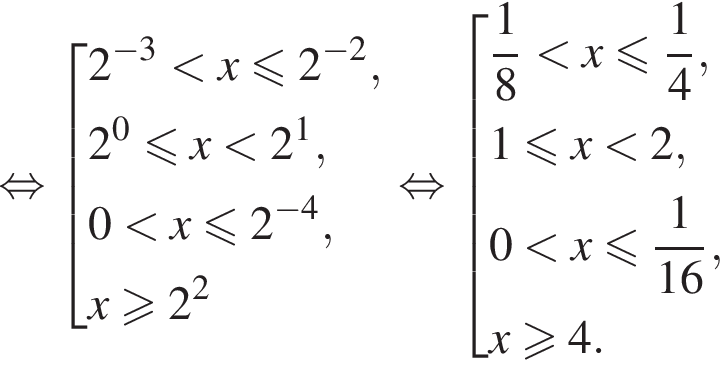











 и
и 


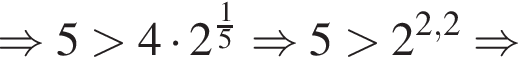













 Оценим значение правой части неравенства:
Оценим значение правой части неравенства:






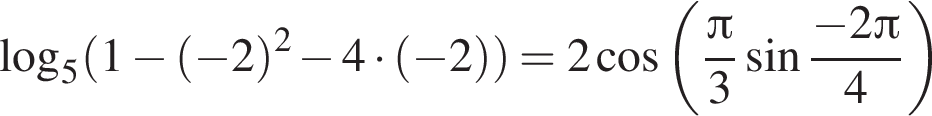 — верно.
— верно.




 то
то



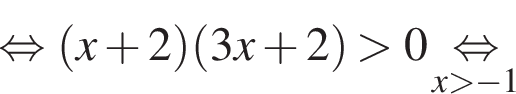


 получим:
получим: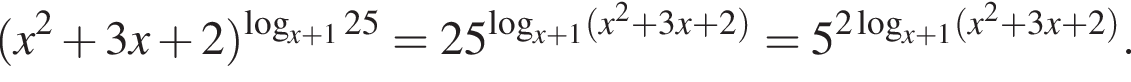






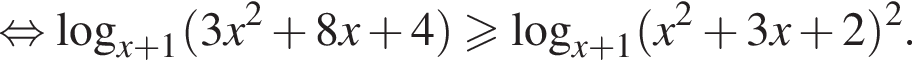
 и
и  равносильны. Отсюда получаем:
равносильны. Отсюда получаем:

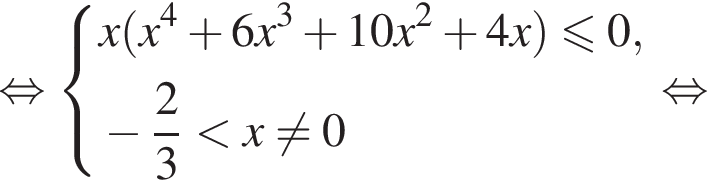
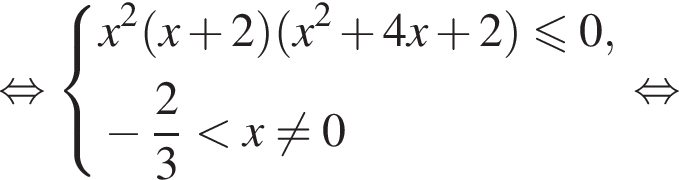



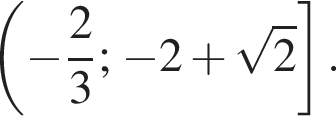

 принимают только положительные значения. Поэтому неравенство верно тогда и только тогда, когда на ОДЗ выполнено неравенство
принимают только положительные значения. Поэтому неравенство верно тогда и только тогда, когда на ОДЗ выполнено неравенство  Получаем:
Получаем:





