
Четырехугольник ABCD описан около окружности и вписан в окружность. Прямые AB и DC пересекаются в точке M. Найдите площадь четырехугольника, если известно, что ∠AMD = α и радиусы окружностей, вписанных в треугольники BCM и AMD равны соответственно r и R.
Решение. Первый случай.
Центры O1 и O окружностей, вписанных в треугольники BMC и AMD соответственно, лежат на биссектрисе MO угла AMD. Окружность, вписанная в четырехугольник ABCD, является также окружностью, вписанной в треугольник AMD и вневписанной окружностью треугольника BMC. Будем искать площадь четырехугольника ABCD, как разность площадей треугольников AMD и BMC.
Четырехугольник ABCD вписан в окружность, следовательно, ∠BAD + ∠BCD = 180°, но ∠BCM + ∠BCD = 180°, откуда ∠BCM = ∠BAD. Так как треугольники BCM и AMD имеют еще общий угол AMD, они подобны, причем коэффициент подобия равен отношению радиусов окружностей, вписанных в эти треугольники.
Далее имеем:
1) 

2)  где p — полупериметр треугольника BCM, равный по свойству вневписанной окружности длине отрезка KM.
где p — полупериметр треугольника BCM, равный по свойству вневписанной окружности длине отрезка KM.
3) Из прямоугольного треугольника OKM, находим  откуда
откуда 
Подставляя найденное значение SΔBCM в формулу SABCD, окончательно получаем



Второй случай.
Отличается от первого положением точки M левее точек D и A. В этом случае R < r и в рассуждении они и треугольники BCM и ADM должны быть поменяны местами. Таким образом, в этом случае

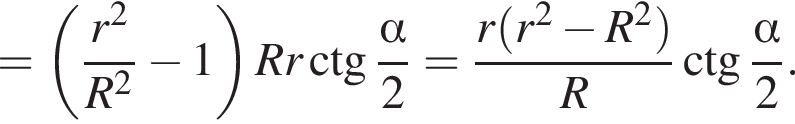



Ответ:  или
или 
| Критерии оценивания ответа на задание С4 | Баллы |
|---|---|
| Обоснованно получен верный ответ | 3 |
| Рассмотрена хотя бы одна возможная геотметрическая конфигурация, для которой получено правильное значениеискомой величины, или рассмотрены обе конфигурации, для которых получены значения искомой величины, неправильные из-за арифметических ошибок. | 2 |
| Рассмотрена хотя бы одна возможная геометрическая конфигурация, для которой получен значение искомой величины, неправильное из-за арифметической ошибки | 1 |
| Решение не соответсвует ни одному из критериев, перечисленных выше | 0 |
| Максимальное количество баллов | 3 |
 или
или 
 или
или 

























 или
или  откуда находим, что r = 6.
откуда находим, что r = 6. из которого найдём, что
из которого найдём, что 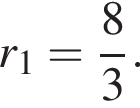
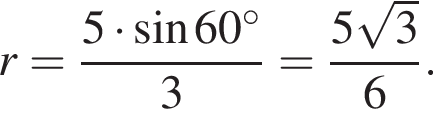

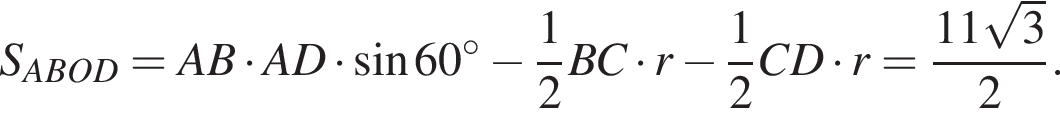

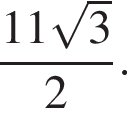








 а
а 

 Тогда
Тогда



 Высота треугольника AOD, проведённая из вершины O, равна
Высота треугольника AOD, проведённая из вершины O, равна 
























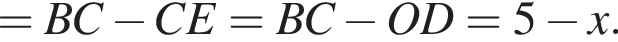



 По теореме Пифагора:
По теореме Пифагора: 



 находим, что
находим, что 


 находим, что x = 5 (это значит, что OD = BC, то есть точка E совпадает с вершиной B).
находим, что x = 5 (это значит, что OD = BC, то есть точка E совпадает с вершиной B).


 По теореме косинусов
По теореме косинусов  Заметим, что так как O1 и O2 — центры описанных окружностей, то прямая O1O2 — серединный перпендикуляр к диагонали BD и является биссектрисой центрального угла BO1D равного 2α. Cледовательно,
Заметим, что так как O1 и O2 — центры описанных окружностей, то прямая O1O2 — серединный перпендикуляр к диагонали BD и является биссектрисой центрального угла BO1D равного 2α. Cледовательно,  поэтому
поэтому 




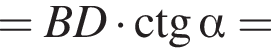






 Поскольку ∠ABO1 = ∠ACO2, прямые O1B и O2C параллельны, следовательно, искомый четырёхугольник — трапеция O1BCO2.
Поскольку ∠ABO1 = ∠ACO2, прямые O1B и O2C параллельны, следовательно, искомый четырёхугольник — трапеция O1BCO2.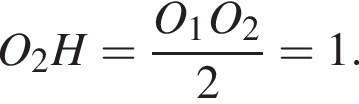

 Поскольку ∠ABO1 = ∠ACO2, прямые O1B и CO2 параллельны. следовательно, искомый четырёхугольник — трапеция O1BO2C.
Поскольку ∠ABO1 = ∠ACO2, прямые O1B и CO2 параллельны. следовательно, искомый четырёхугольник — трапеция O1BO2C.


 откуда
откуда 

 Таким образом,
Таким образом, 
 или
или 





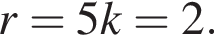
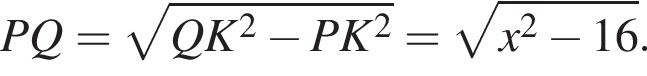
 откуда
откуда 





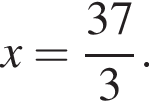



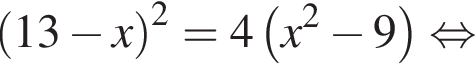



 Обозначим
Обозначим 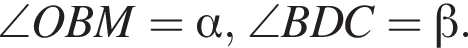 Из прямоугольных треугольников и находим, что
Из прямоугольных треугольников и находим, что 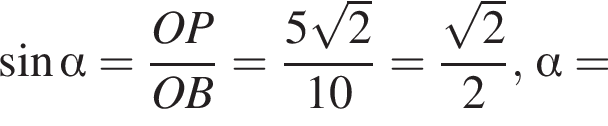


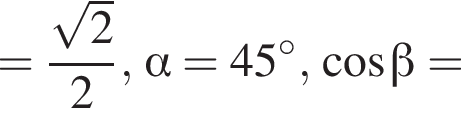
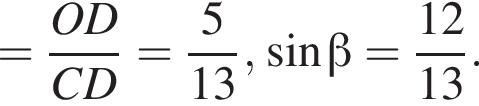
 поэтому
поэтому



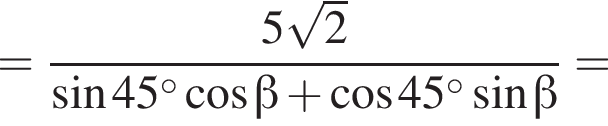








 с коэффициентом подобия
с коэффициентом подобия 



 получаем:
получаем: 










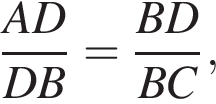 то есть
то есть 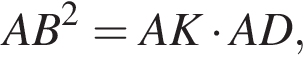 то есть
то есть  Следовательно,
Следовательно, 

 а значит, AB = BD. Из подобия треугольников ABD и DCB находим, что BC = CD. Используя следствие из теоремы косинусов, находим
а значит, AB = BD. Из подобия треугольников ABD и DCB находим, что BC = CD. Используя следствие из теоремы косинусов, находим 



 Имеем:
Имеем:


 Получаем, что
Получаем, что  Пусть AC = 10x, тогда: AB = 6x, BC = 8x и
Пусть AC = 10x, тогда: AB = 6x, BC = 8x и 