1.
i
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 103°, угол CAD равен 42°. Найдите угол ABD. Ответ дайте в градусах.
ИЛИ
Площадь параллелограмма ABCD равна 24. Точка E — середина стороны AD. Найдите площадь трапеции BCDE.
ИЛИ
В треугольнике ABC AC = BC, угол C равен 134°. Найдите внешний угол CBD. Ответ дайте в градусах.
ИЛИ
Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.
Следовательно, 
Площадь трапеции BCDE равна
и 
Найдите скалярное произведение 
Найдите длину вектора 
Скалярное произведение векторов равно:
высоты. Объём жидкости равен 4 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
и 
а второй кружки — за 
и 
Первая кружка в два раза выше второй, тогда 
Вторая кружка в полтора раза шире первой, тогда 
Тогда объем первой кружки равен
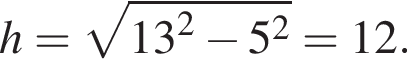Тогда площадь поверхности пирамиды 
Объемы подобных тел относятся как куб коэффициента подобия. Поэтому объем большего конуса в 27 раз больше объема меньшего конуса, он равен 108 мл. Следовательно, необходимо долить 108 − 4 = 104 мл жидкости.
Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
если 
Получаем:
производной функции f(x). На оси абсцисс отмечено десять точек: x1, x2, x3, x4, x5, x6, x7, x8, x9, x10. Сколько из этих точек принадлежит промежуткам возрастания функции f(x)?
и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Гц. Чуть позже издал гудок подъезжающий к платформе тепловоз. Из-за эффекта Доплера частота второго гудка f больше первого: она зависит от скорости тепловоза по закону 
(Гц), где c — скорость звука (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 5 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а 
м/с. Ответ выразите в м/с.
при известном значении постоянной 
Гц:
Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 72-процентный раствор кислоты: 
литров воды в минуту. Резервуар объемом 104 литра первая труба заполняет на 5 минут дольше, чем вторая труба, отсюда имеем:
и 
пересекающиеся в точках A и B. Найдите абсциссу точки B.
откуда 
Составим систему уравнений и найдем коэффициенты a и b:
на отрезке 
заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение:
б) 
и 
и 
Площадь SRTK равна:
не определено при 
равно нулю при 
и при 
и положительно при других значениях x. При 
и 
неравенство принимает вид: 
Учитывая условия 
получаем: 
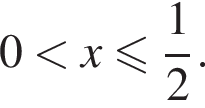
тогда проценты, начисленные с 2026 по 2035 год, составят: 
и 
и 
По свойству пересекающихся хорд получаем:
Таким образом, 
следовательно, 
откуда 
либо является решением системы: 
при условии 
и найдём количество корней получившегося уравнения в зависимости от a. 
откуда 
при условии 
Дискриминант этого уравнения равен 
имеет два корня при 
имеет единственный корень x = 4 при 
и не имеет корней при 
функция 
принимает наименьшее значение при x = 4, и это значение отрицательно. Следовательно, больший корень уравнения 
удовлетворяет условию 
тогда и только тогда, когда 
откуда 
удовлетворяет условию 
откуда 
Число 
является корнем квадратного уравнения 
Таким образом, исходная система уравнений имеет ровно два различных решения при 
за один ход получают пару (a + b; a – b).
поэтому второй ход даст 
Дальше все пары будут либо вида 
либо вида 
Поскольку 806 кратно 31, а ни одно из чисел в этих парах не кратно 31, получить его нельзя.
и 
откуда 
и 