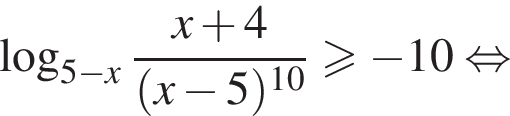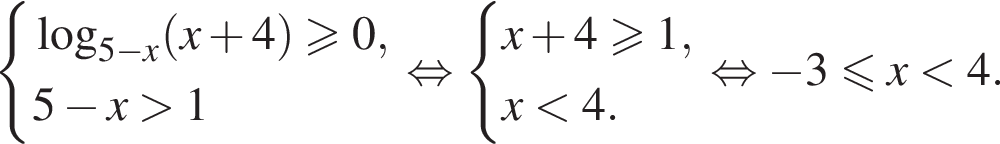1. Тип Д11 C3 № 484597 

Классификатор алгебры: Неравенства с логарифмами по переменному основанию, Системы неравенств
Методы алгебры: Группировка
Простые системы неравенств. Системы с логарифмами по переменному основанию
i
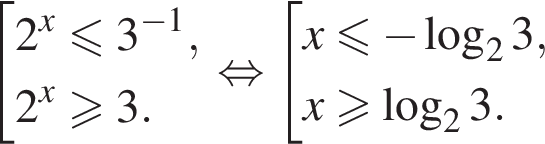
Решите систему неравенств 
Решение. Область допустимых значений первого неравенства задается соотношениями:
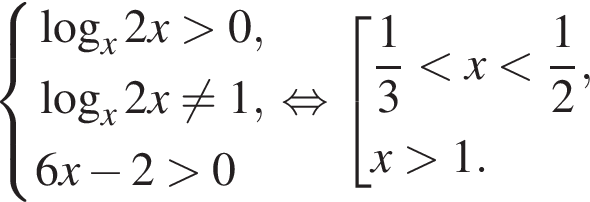
На области допустимых значений справедливы равносильности:


Поэтому на ОДЗ имеем:









Заметим, что









Поэтому







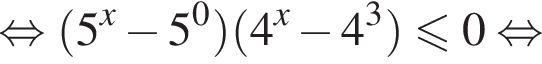
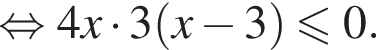
Окончательно имеем:






Ответ: 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 3 |
| Обоснованно получены верные ответы в обоих неравенствах системы неравенств | 2 |
| Обоснованно получен верный ответ в одном из неравенств системы неравенств | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ответ: 

484597

Классификатор алгебры: Неравенства с логарифмами по переменному основанию, Системы неравенств
Методы алгебры: Группировка








 неравенство
неравенство  определено, и его знак совпадает со знаком произведения
определено, и его знак совпадает со знаком произведения  Поскольку на указанном отрезке числитель и знаменатель первой дроби положительны, получаем:
Поскольку на указанном отрезке числитель и знаменатель первой дроби положительны, получаем: 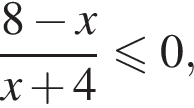 откуда
откуда  или
или 
 и
и  Рассмотрим два случая.
Рассмотрим два случая. 
 Тогда
Тогда





 Получаем, что
Получаем, что 
 следовательно, при
следовательно, при 

 На этом множестве основание и аргумент множителя
На этом множестве основание и аргумент множителя  оба больше 1, поэтому он положителен. Тогда остаётся решить неравенство
оба больше 1, поэтому он положителен. Тогда остаётся решить неравенство  что на ОДЗ даёт
что на ОДЗ даёт  откуда
откуда  и окончательно с учётом ОДЗ:
и окончательно с учётом ОДЗ: 




 При
При  будем также иметь:
будем также иметь: 




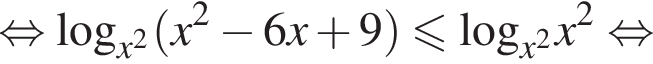









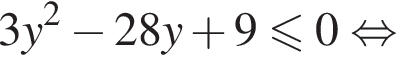



 откуда находим решение первого неравенства системы:
откуда находим решение первого неравенства системы: 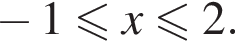




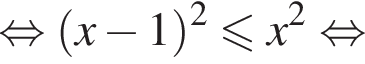
 получаем:
получаем: 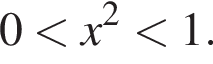


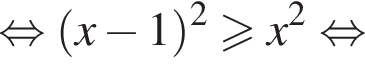
 получаем
получаем 







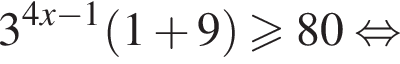

 при всех
при всех 



 имеем
имеем  откуда получаем множество решений системы:
откуда получаем множество решений системы: 








 при всех
при всех 


 или
или  поэтому
поэтому  Следовательно,
Следовательно, или
или 







 или
или  откуда находим:
откуда находим:  или
или 

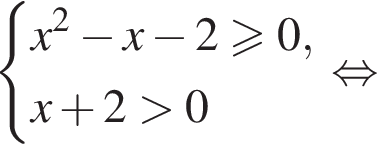
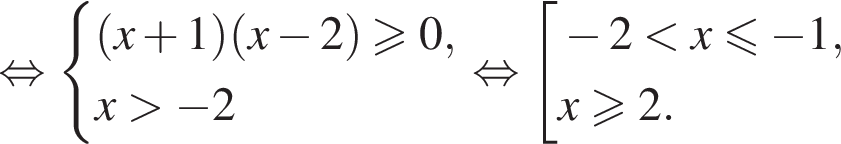
 получаем:
получаем:  или
или 



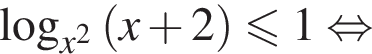

 получаем:
получаем:  или
или 

 получим множество решений исходной системы неравенств:
получим множество решений исходной системы неравенств: 




 или
или  откуда:
откуда:  или
или 

 или
или 




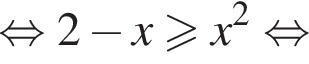


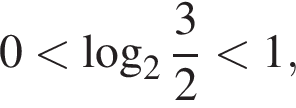 получаем решение исходной системы неравенств:
получаем решение исходной системы неравенств: 


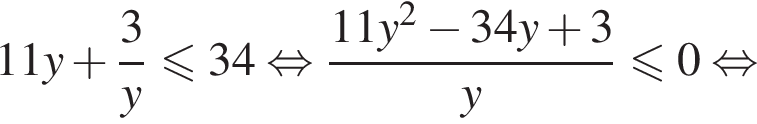


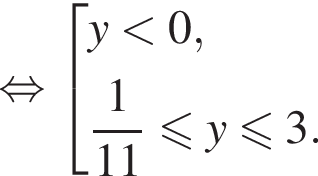


 получаем:
получаем: 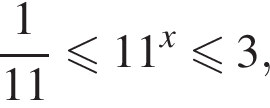 откуда множество решение первого неравенства
откуда множество решение первого неравенства 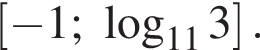




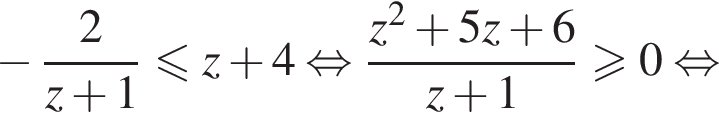



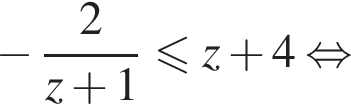


 получаем решение исходной системы неравенств:
получаем решение исходной системы неравенств: 








 получаем:
получаем:  откуда получаем множество решений первого неравенства
откуда получаем множество решений первого неравенства 







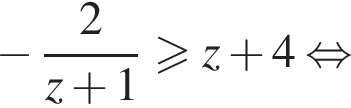

 или
или  откуда получаем множество решений второго неравенства
откуда получаем множество решений второго неравенства 
 получаем решение исходной системы неравенств:
получаем решение исходной системы неравенств: 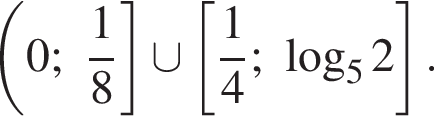







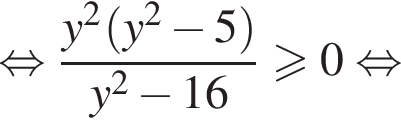
 получаем
получаем  или
или  откуда находим множество решений первого неравенства системы:
откуда находим множество решений первого неравенства системы: 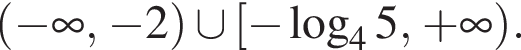







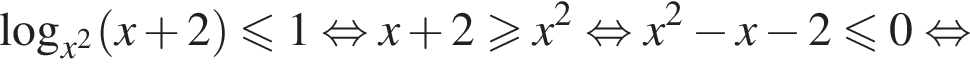






 получаем множество решений исходной системы
получаем множество решений исходной системы 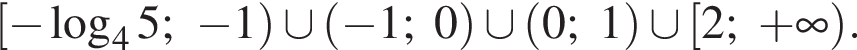








 или
или 



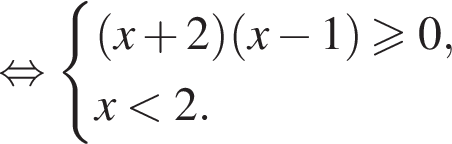






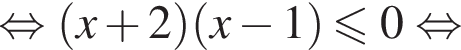



 получаем решение исходной системы неравенств:
получаем решение исходной системы неравенств: 

 тогда данное неравенство принимает вид
тогда данное неравенство принимает вид 
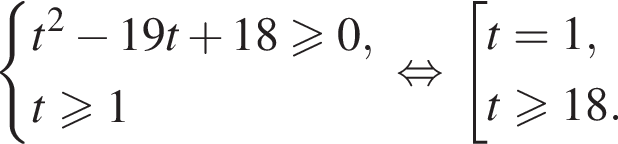



 и
и  исходное неравенство равносильно неравенству:
исходное неравенство равносильно неравенству: 
 получаем:
получаем: 


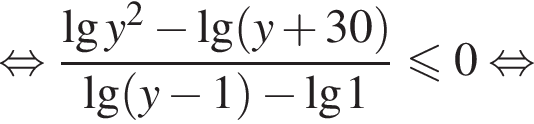









 получаем множество решений второго неравенства:
получаем множество решений второго неравенства: 


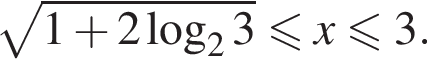


 тогда данное неравенство принимает вид
тогда данное неравенство принимает вид 




 и
и  исходное неравенство равносильно неравенству
исходное неравенство равносильно неравенству
 получаем
получаем 





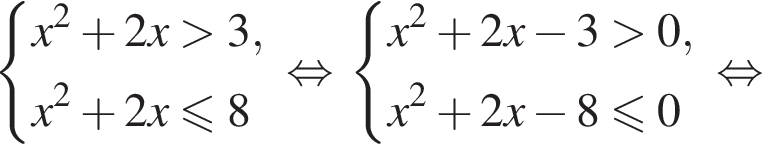
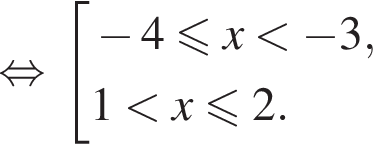


 получаем решения второго неравенства:
получаем решения второго неравенства: 










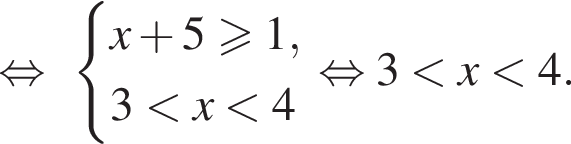
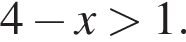




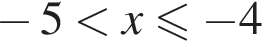 или
или 
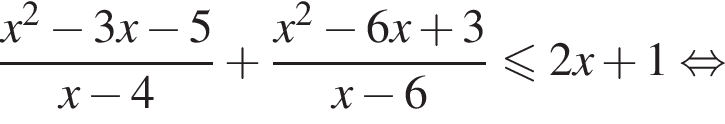


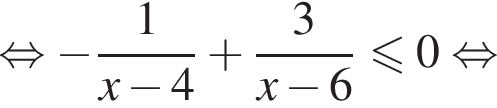


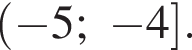











 или
или 







 Рассмотрим два случая.
Рассмотрим два случая. 
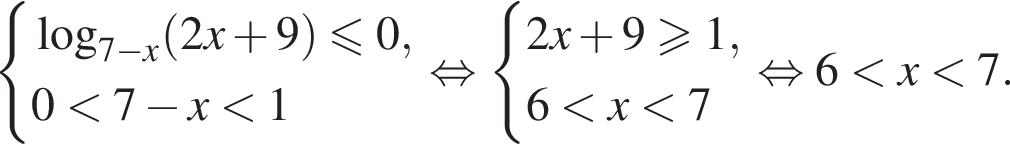










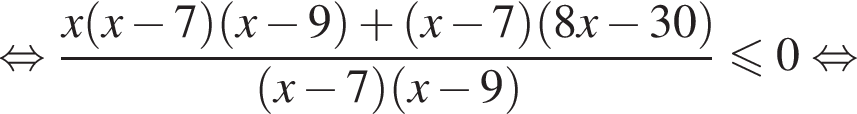









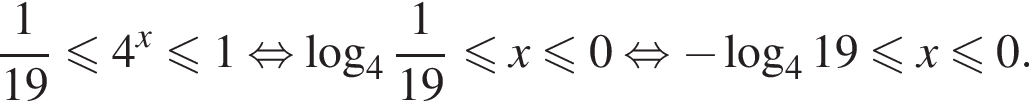




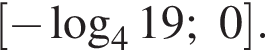







 неположителен. Тогда второе неравенство можно решить иначе. Отметим, что число 0 является его решением и рассмотрим значения
неположителен. Тогда второе неравенство можно решить иначе. Отметим, что число 0 является его решением и рассмотрим значения  Поскольку при
Поскольку при  откуда
откуда  Вместе с числом 0 это и даёт ответ.
Вместе с числом 0 это и даёт ответ.
 Тогда имеем систему:
Тогда имеем систему:



 Тогда имеем систему:
Тогда имеем систему:







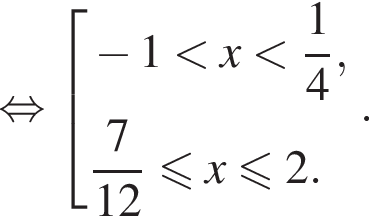


 Тогда имеем систему
Тогда имеем систему


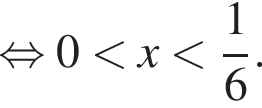
 Тогда имеем систему:
Тогда имеем систему:
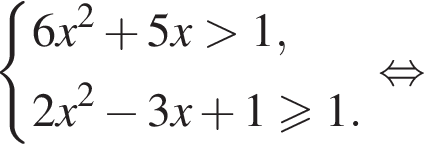

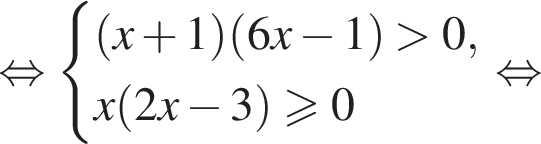













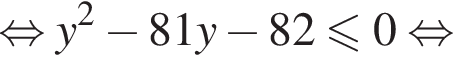
 откуда находим решение первого неравенства системы
откуда находим решение первого неравенства системы 




 Полученные значения переменной удовлетворяют условию
Полученные значения переменной удовлетворяют условию 
 Имеем:
Имеем:







 получаем:
получаем:  Решение второго неравенства исходной системы:
Решение второго неравенства исходной системы: 
 получаем решение исходной системы неравенств:
получаем решение исходной системы неравенств:


 получаем:
получаем:  Из
Из 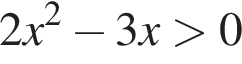 получаем:
получаем: 
 получаем:
получаем:  откуда
откуда 



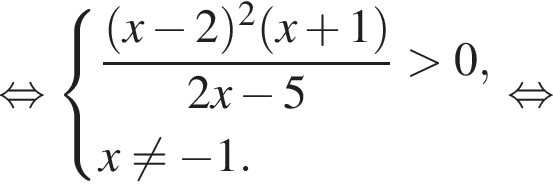










 откуда находим решение первого неравенства системы:
откуда находим решение первого неравенства системы: 
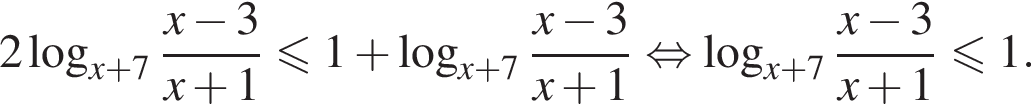













 получаем:
получаем:  Множество решений второго неравенства исходной системы:
Множество решений второго неравенства исходной системы: 
 получаем решение исходной системы неравенств:
получаем решение исходной системы неравенств: 

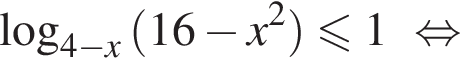


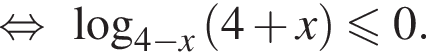

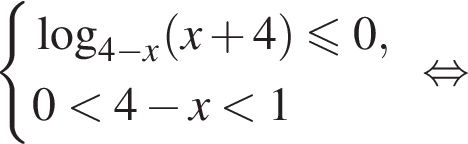





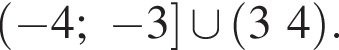















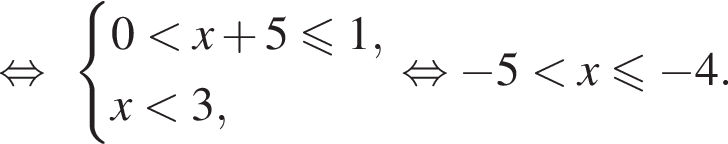













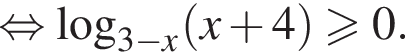







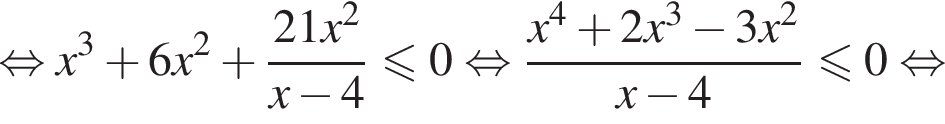
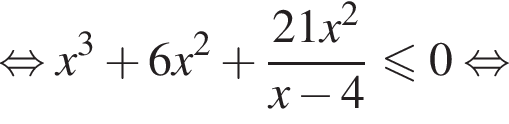


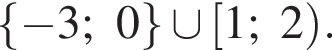
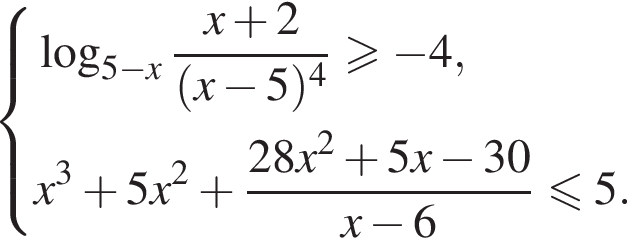




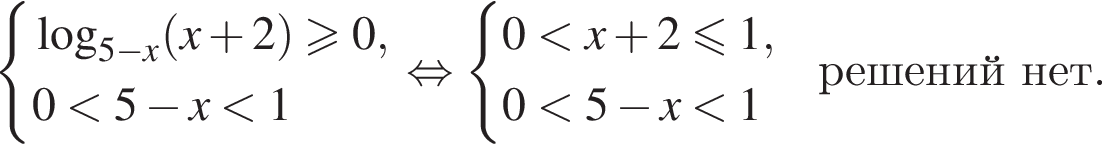



















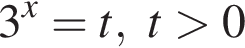 тогда данное неравенство принимает вид:
тогда данное неравенство принимает вид:
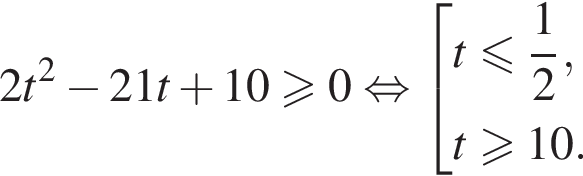
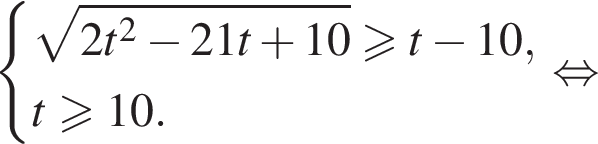









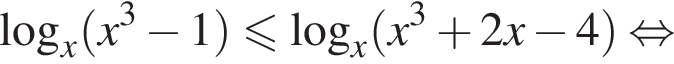




 тогда данное неравенство принимает вид:
тогда данное неравенство принимает вид:

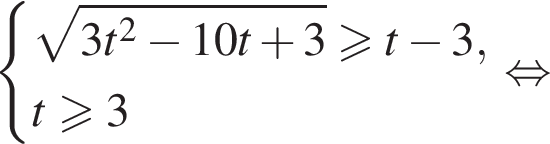

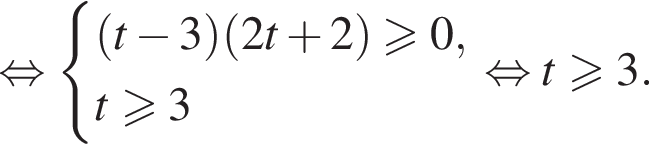





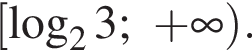








 получим
получим  откуда
откуда 
 откуда
откуда 
 имеем:
имеем:
 Имеем:
Имеем:





 получаем решение исходной системы неравенств:
получаем решение исходной системы неравенств: 




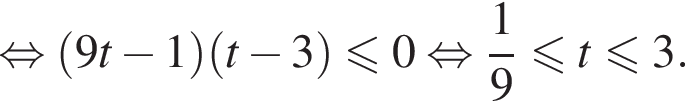






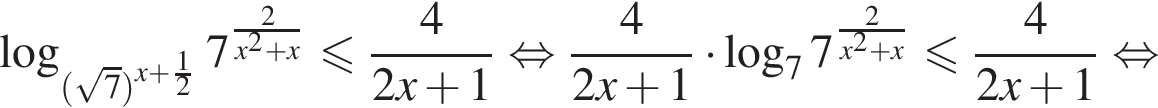

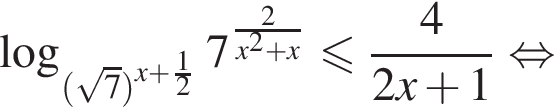


















 получаем решение исходной системы неравенств:
получаем решение исходной системы неравенств: 
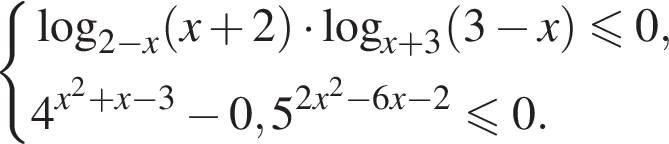
 и
и  Получаем, что
Получаем, что  Тогда:
Тогда: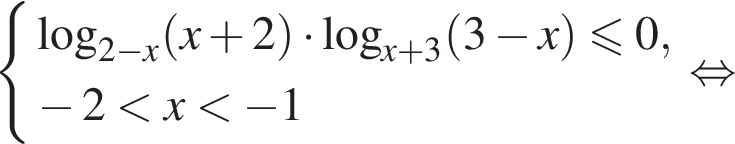




 следовательно, при
следовательно, при  первое неравенство исходной системы верно.
первое неравенство исходной системы верно.













 то
то
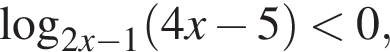 то
то

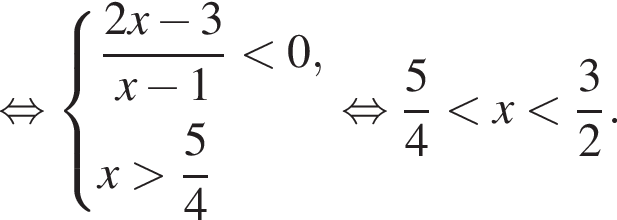


 или
или 
 Получаем
Получаем 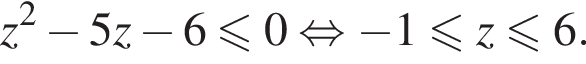

 находим решение системы:
находим решение системы: 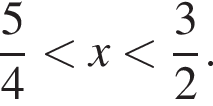


 откуда
откуда  Таким образом,
Таким образом, 
 и
и  для любого
для любого  и методом интервалов, получаем:
и методом интервалов, получаем:





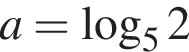 и
и  Имеем
Имеем 
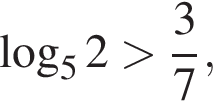 откуда и получаем решение данной системы:
откуда и получаем решение данной системы: 
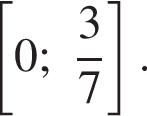



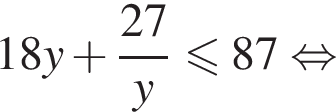



 получаем:
получаем: 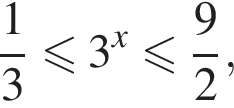 откуда находим решение первого неравенства системы:
откуда находим решение первого неравенства системы: 
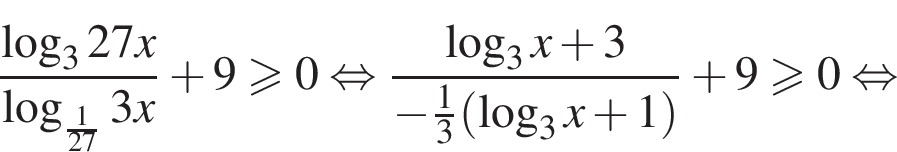







 или
или  откуда
откуда  или
или  Пересекая полученные решения найдём множество решений исходной системы неравенств:
Пересекая полученные решения найдём множество решений исходной системы неравенств: 
 Имеем:
Имеем:




 Решение первого неравенства исходной системы:
Решение первого неравенства исходной системы: 
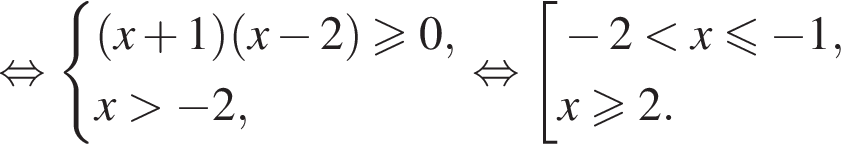







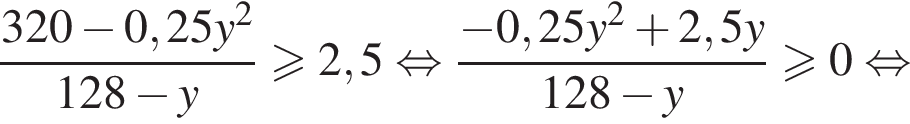





 или
или  откуда находим множество решений первого неравенства системы:
откуда находим множество решений первого неравенства системы: 





 получаем:
получаем:  или
или 
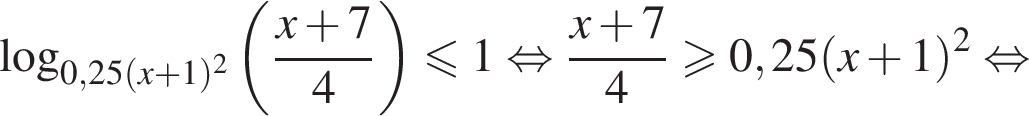



 получаем:
получаем: 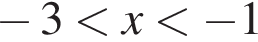 или
или 

 получаем решение исходной системы неравенств:
получаем решение исходной системы неравенств:




 то
то
 то
то 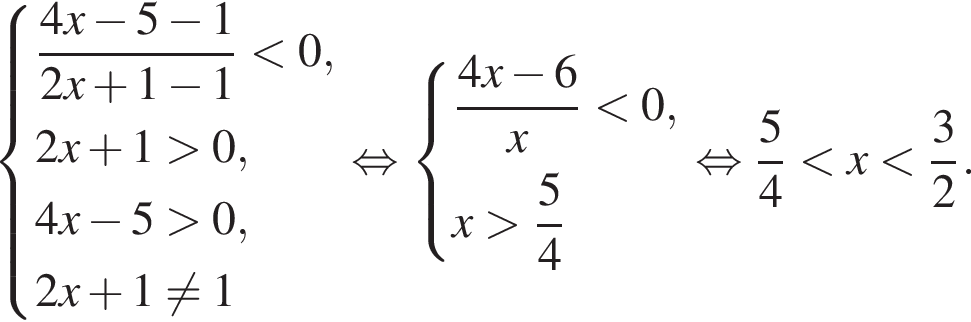

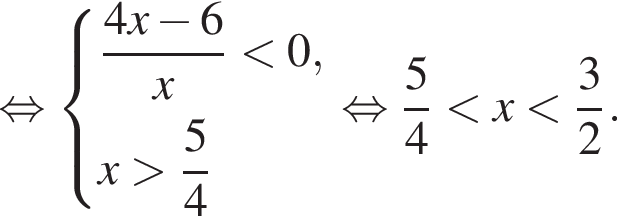




 Получаем:
Получаем: 
 то есть
то есть 
 находим решение системы:
находим решение системы: 

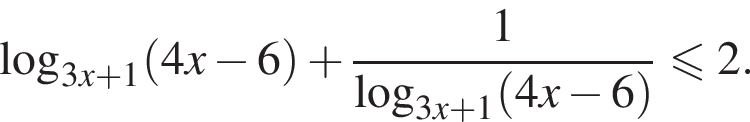




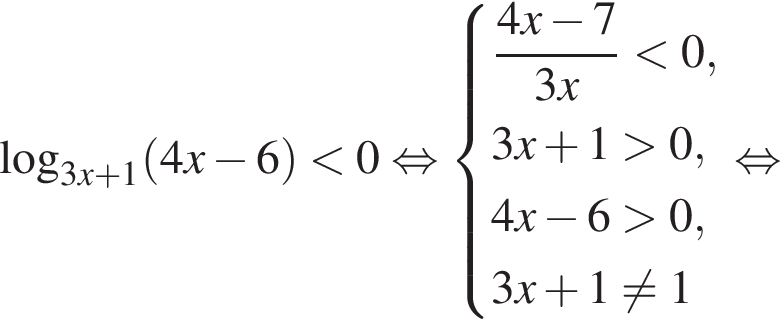

 или
или 
 имеем:
имеем:  Откуда, возвращаясь к исходной переменной, получим:
Откуда, возвращаясь к исходной переменной, получим:
 находим решение системы.
находим решение системы.

 то есть при
то есть при  Тогда неравенство принимает вид
Тогда неравенство принимает вид  откуда
откуда 




 :
: 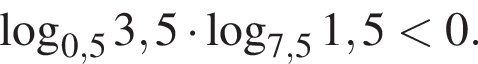
 :
: 
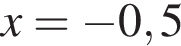 :
: 


 то есть при
то есть при  Тогда неравенство принимает вид
Тогда неравенство принимает вид 







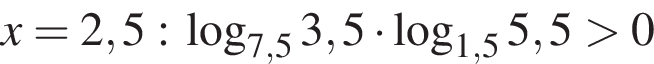


 и
и 






 и
и  а значит,
а значит,  и
и 





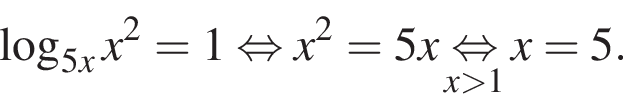




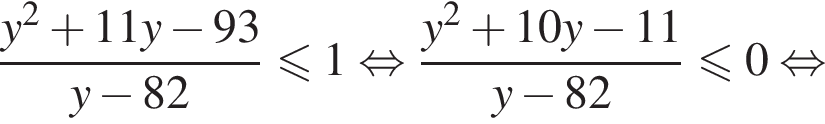





 получаем:
получаем:  откуда находим решение первого неравенства системы
откуда находим решение первого неравенства системы 




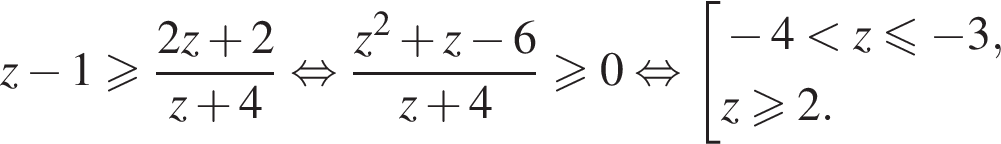




 или
или  откуда находим решение второго неравенства системы:
откуда находим решение второго неравенства системы: 
 получаем решение исходной системы неравенств:
получаем решение исходной системы неравенств: 


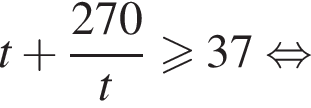



 получим:
получим:








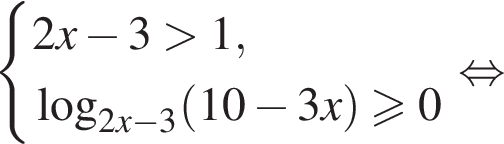




 получаем решение исходной системы неравенств:
получаем решение исходной системы неравенств: 








 тогда неравенство примет вид:
тогда неравенство примет вид: 





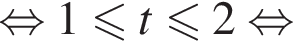







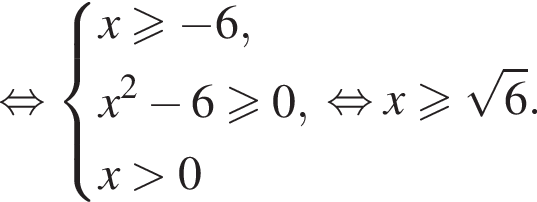



 получаем решение исходной системы неравенств:
получаем решение исходной системы неравенств: