
Найдите все значения a, при каждом из которых уравнение



имеет хотя бы одно решение, меньшее 2.
Решение. Сделаем замену  Поскольку
Поскольку 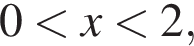 то
то  и каждому такому t соответствует единственное
и каждому такому t соответствует единственное ![]()
Получаем задачу — при каких a уравнение 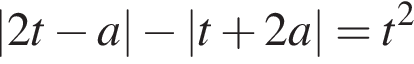 имеет корень, больший чем
имеет корень, больший чем ![]() ?
?
Построим график этого уравнения в плоскости tOa.
Прямые ![]() и
и  разбивают плоскость на четыре части (I, II, III и IV), в каждой из которых график уравнения
разбивают плоскость на четыре части (I, II, III и IV), в каждой из которых график уравнения  представляет собой часть параболы.
представляет собой часть параболы.
В области I оба подмодульных выражения положительны и уравнение принимает вид

Графиком 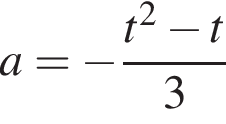 является парабола с вершиной в точке с координатами
является парабола с вершиной в точке с координатами 
В области II выражение ![]() отрицательно, а выражение
отрицательно, а выражение ![]() положительно и уравнение принимает вид
положительно и уравнение принимает вид
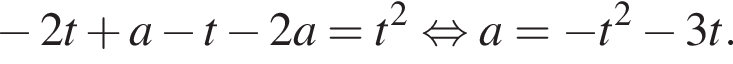
Графиком  является парабола с вершиной в точке с координатами
является парабола с вершиной в точке с координатами 
Для области III получим

Графиком  является парабола с вершиной в точке с координатами
является парабола с вершиной в точке с координатами 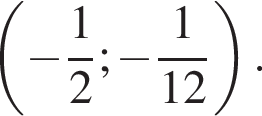
Для области IV получим

Графиком  является парабола с вершиной в точке с координатами
является парабола с вершиной в точке с координатами 
Задача свелась к ответу на вопрос: при каких значениях a, горизонтальная прямая имеет пересечение с графиком функции правее вертикальной прямой  (красная линия).
(красная линия).
Получаем ответ: при
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен правильный ответ. | 4 |
| С помощью верного рассуждения получены оба верных значения параметра, но – или в ответ включены также и одно-два неверных значения; – или решение недостаточно обосновано. | 3 |
| С помощью верного рассуждения получено хотя бы одно верное значение параметра. | 2 |
| Задача сведена к исследованию: – или взаимного расположения трёх окружностей; – или двух квадратных уравнений с параметром. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |


 получаем:
получаем:










 Наибольшая разность корней достигается в том случае, когда эта прямая содержит диаметр окружности, то есть при a = 2.
Наибольшая разность корней достигается в том случае, когда эта прямая содержит диаметр окружности, то есть при a = 2.





 (здесь a — значение параметра). Квадратичная функция
(здесь a — значение параметра). Квадратичная функция  с отрицательным старшим коэффициентом достигает наибольшего значения в точке
с отрицательным старшим коэффициентом достигает наибольшего значения в точке  Проверим, что при найденном значении параметра подкоренное выражение неотрицательно:
Проверим, что при найденном значении параметра подкоренное выражение неотрицательно:  Следовательно, наибольшее значение модуля разности достигается при a = 2.
Следовательно, наибольшее значение модуля разности достигается при a = 2.





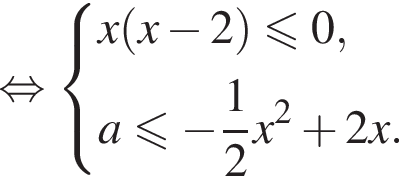
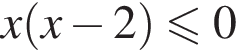 определяет на плоскости Oxa полосу, заключенную между прямыми
определяет на плоскости Oxa полосу, заключенную между прямыми 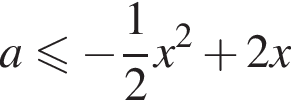 задаёт часть плоскости, ограниченную сверху параболой.
задаёт часть плоскости, ограниченную сверху параболой. это означает, что на интервале
это означает, что на интервале 








 то множеством решений данного неравенства также является не луч, а объединение двух промежутков:
то множеством решений данного неравенства также является не луч, а объединение двух промежутков:  (см. рис. 1).
(см. рис. 1). то
то 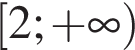 (см. рис. 2).
(см. рис. 2). ).
).

 то неравенство, а значит, и система не имеет решений.
то неравенство, а значит, и система не имеет решений.  то решение неравенства — луч
то решение неравенства — луч 
 то решение неравенства — луч
то решение неравенства — луч 
 первое неравенство системы принимает вид
первое неравенство системы принимает вид
 Очевидно, что при
Очевидно, что при  решение системы будет содержать луч вида
решение системы будет содержать луч вида  где b — большее из чисел
где b — большее из чисел  и
и  а значит, система будет иметь решение.
а значит, система будет иметь решение. первое неравенство исходной системы, а значит, и система не будет иметь решений. В остальных случаях решением первого неравенства исходной системы будет полуинтервал с концами в точках
первое неравенство исходной системы, а значит, и система не будет иметь решений. В остальных случаях решением первого неравенства исходной системы будет полуинтервал с концами в точках  Отметим, что точки
Отметим, что точки  нет во множестве решений первого неравенства.
нет во множестве решений первого неравенства. 



 получаем ответ.
получаем ответ.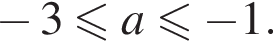
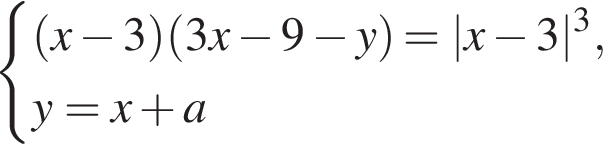
 и заметим, что
и заметим, что  Очевидно, число решений системы будет совпадать с числом решений уравнения
Очевидно, число решений системы будет совпадать с числом решений уравнения 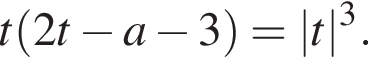 Очевидно,
Очевидно, 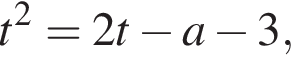
 Это уравнение имеет два положительных корня, если
Это уравнение имеет два положительных корня, если  то есть при
то есть при  и один положительный корень при
и один положительный корень при 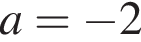 или
или 

 Это уравнение имеет два отрицательных корня, если
Это уравнение имеет два отрицательных корня, если  то есть при
то есть при  и один отрицательный корень при
и один отрицательный корень при  или
или 
 система будет иметь два решения;
система будет иметь два решения; система будет иметь четыре решения;
система будет иметь четыре решения; система будет иметь три решения;
система будет иметь три решения; система будет иметь четыре решения;
система будет иметь четыре решения; система будет иметь два решения.
система будет иметь два решения.

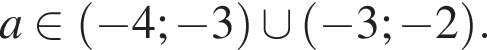
 или
или  ; возможно, с включением граничных точек.
; возможно, с включением граничных точек.






 неравенство не имеет решений.
неравенство не имеет решений. решением являются все точки, лежащие правее прямой
решением являются все точки, лежащие правее прямой 

 решением являются все точки между прямыми
решением являются все точки между прямыми 
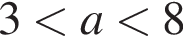 решением являются все точки, лежащие правее правой ветви параболы
решением являются все точки, лежащие правее правой ветви параболы  и левее прямой
и левее прямой 



 пересекаются в точке A(2; 1). Гипербола и прямая
пересекаются в точке A(2; 1). Гипербола и прямая 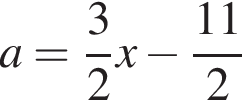 пересекаются в точке
пересекаются в точке  График корня и прямая пересекаются в точке C(5; 2). Множество точек, координаты которых удовлетворяют заданной системе (выделено штриховкой на рисунке), состоит из точек криволинейного треугольника ABC, не включая границу, лежащую на дуге АС.
График корня и прямая пересекаются в точке C(5; 2). Множество точек, координаты которых удовлетворяют заданной системе (выделено штриховкой на рисунке), состоит из точек криволинейного треугольника ABC, не включая границу, лежащую на дуге АС. дают искомое множество: заданная система неравенств имеет хотя бы одно решение на отрезке [3; 4] при
дают искомое множество: заданная система неравенств имеет хотя бы одно решение на отрезке [3; 4] при 


 имеющий общие точки с отрезком [3; 4].
имеющий общие точки с отрезком [3; 4]. Тогда решением системы является отрезок
Тогда решением системы является отрезок  Он существует, если
Он существует, если





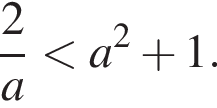 В этом случае решением системы является полуинтервал
В этом случае решением системы является полуинтервал  Этот полуинтервал существует, если
Этот полуинтервал существует, если



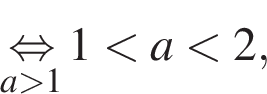
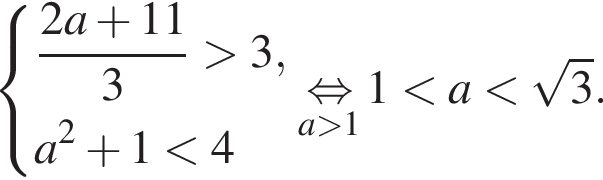



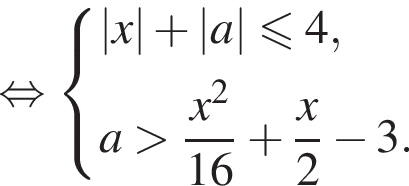


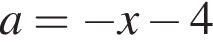 и
и  а неравенство
а неравенство  задаёт часть плоскости выше параболы с вершиной (−4; −4), ветви которой направлены вверх. Найдём координаты точки A пересечения параболы с прямой
задаёт часть плоскости выше параболы с вершиной (−4; −4), ветви которой направлены вверх. Найдём координаты точки A пересечения параболы с прямой 


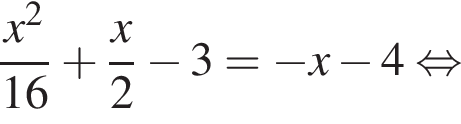



 соответствует точке пересечения, лежащей во второй четверти. Для большего корня справедливы неравенства:
соответствует точке пересечения, лежащей во второй четверти. Для большего корня справедливы неравенства:
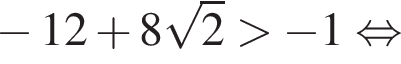
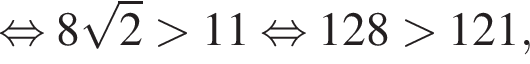


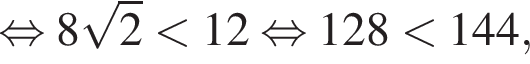
 находим:
находим: 

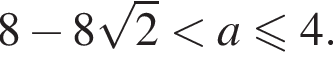


 и двух тупых углов, ограниченных прямыми
и двух тупых углов, ограниченных прямыми  и
и 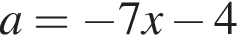 (см. рис., выделено жирным контуром). Найдём абсциссы их точек пересечения.
(см. рис., выделено жирным контуром). Найдём абсциссы их точек пересечения.





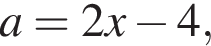 то есть для всех a из отрезка
то есть для всех a из отрезка и для
и для 
 при
при  при
при  при
при  при
при 




 При
При  исходная система принимает вид:
исходная система принимает вид:
 поскольку
поскольку  Поэтому при
Поэтому при 
 откуда
откуда  Заметим, что максимальное значение функции
Заметим, что максимальное значение функции  на отрезке
на отрезке  равно
равно  Кроме того, при
Кроме того, при 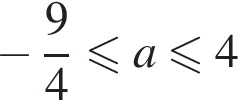 больший корень уравнения
больший корень уравнения  удовлетворяет системе неравенств, поскольку функция
удовлетворяет системе неравенств, поскольку функция  Таким образом, исходная система неравенств имеет хотя бы одной решение при
Таким образом, исходная система неравенств имеет хотя бы одной решение при 
 и/или
и/или  или
или 





 Тогда корень
Тогда корень  принадлежит отрезку [4; 8] и удовлетворяет ОДЗ. Тогда уравнение имеет единственное решение на заданном отрезке, если второй корень не принадлежит отрезку [4; 8] или не удовлетворяет ОДЗ. Имеем:
принадлежит отрезку [4; 8] и удовлетворяет ОДЗ. Тогда уравнение имеет единственное решение на заданном отрезке, если второй корень не принадлежит отрезку [4; 8] или не удовлетворяет ОДЗ. Имеем:




 принадлежит отрезку [4; 8] и удовлетворяет ОДЗ. Тогда уравнение имеет единственное решение на заданном отрезке, если первый корень не принадлежит отрезку [4; 8] или не удовлетворяет ОДЗ. Имеем:
принадлежит отрезку [4; 8] и удовлетворяет ОДЗ. Тогда уравнение имеет единственное решение на заданном отрезке, если первый корень не принадлежит отрезку [4; 8] или не удовлетворяет ОДЗ. Имеем:





 и
и 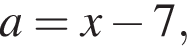 лежащие внутри круга, ограниченного окружностью
лежащие внутри круга, ограниченного окружностью 


 найдём, подставив в уравнение окружности
найдём, подставив в уравнение окружности 




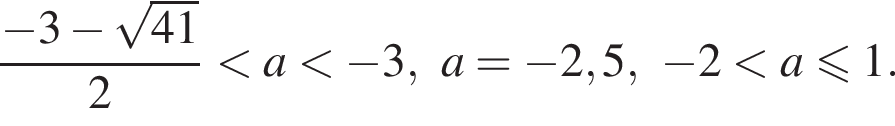



 Прямая
Прямая 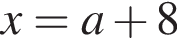 и окружность
и окружность  и
и  Прямая
Прямая  и окружность
и окружность  пересекаются в точках
пересекаются в точках  и
и  Неравенству удовлетворяет, например, точка A(5; 0) — центр окружности. Таким образом, множество точек, координаты которых удовлетворяют уравнению, состоит из дуг BD и CE.
Неравенству удовлетворяет, например, точка A(5; 0) — центр окружности. Таким образом, множество точек, координаты которых удовлетворяют уравнению, состоит из дуг BD и CE. в точках (2; −4) и (2; 4). Прямая x = 6 пересекает окружность
в точках (2; −4) и (2; 4). Прямая x = 6 пересекает окружность  и
и 
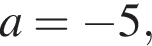
 и
и 
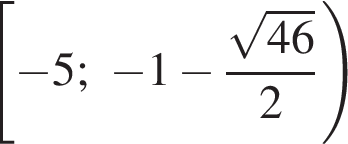 и
и  , множества значений a, возможно, с исключением граничных точек.
, множества значений a, возможно, с исключением граничных точек.






 в плоскости xOa на интервале
в плоскости xOa на интервале При
При  При
При  (см. рис).
(см. рис). и при
и при 

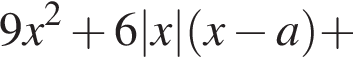






 или при a = 0. При a = −4 уравнение не имеет корней, которые удовлетворяют условию задачи.
или при a = 0. При a = −4 уравнение не имеет корней, которые удовлетворяют условию задачи.


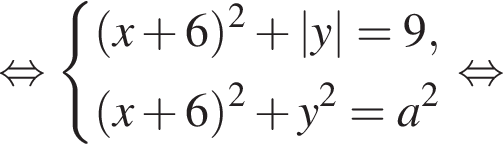

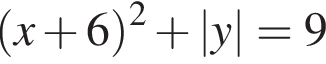 каждому значению переменной y соответствует не более двух значений переменной x, а именно, если
каждому значению переменной y соответствует не более двух значений переменной x, а именно, если  то два значения,
то два значения,  то одно значение,
то одно значение,  то соответствующих значений переменной x не существует. Значит, количество решений системы не превышает удвоенного числа корней уравнения
то соответствующих значений переменной x не существует. Значит, количество решений системы не превышает удвоенного числа корней уравнения  Построим эскиз графика этого уравнения в системе координат
Построим эскиз графика этого уравнения в системе координат 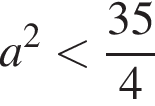 уравнение (⁎), а значит, и исходная система не имеют решений. При
уравнение (⁎), а значит, и исходная система не имеют решений. При  или
или  уравнение (⁎) имеет четыре корня, все эти корни такие, что
уравнение (⁎) имеет четыре корня, все эти корни такие, что 







 лежащих выше и ниже прямой
лежащих выше и ниже прямой  соответственно (см. рис.), пересекающихся в точках
соответственно (см. рис.), пересекающихся в точках 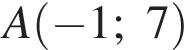 и
и  Количество корней равнения равно количеству точек пересечения графика уравнения с горизонтальной прямой при соответствующем значении a.
Количество корней равнения равно количеству точек пересечения графика уравнения с горизонтальной прямой при соответствующем значении a.  уравнение не имеет корней;
уравнение не имеет корней; уравнение имеет два корня;
уравнение имеет два корня; уравнение имеет три корня;
уравнение имеет три корня;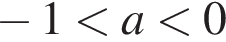 уравнение имеет четыре корня;
уравнение имеет четыре корня; уравнение имеет два корня;
уравнение имеет два корня; уравнение имеет четыре корня;
уравнение имеет четыре корня; уравнение имеет два корня;
уравнение имеет два корня; или при
или при 
