
Найдите все значения а, при каждом из которых решения неравенства  образуют отрезок длины 1.
образуют отрезок длины 1.
Решение. Перенесем единицу: 
Построим схематично графики функций  и
и 
На рисунке видно, что неравенство имеет решения только при  или
или 
1. 
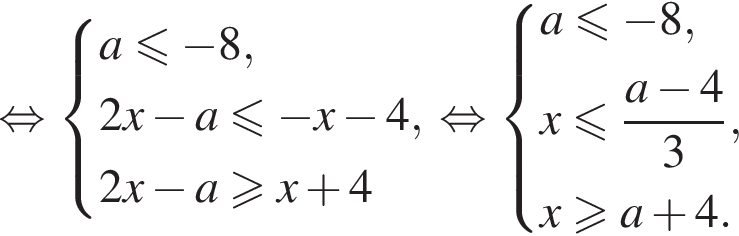
Решения образуют отрезок длины 1, если  откуда
откуда 
2. 
Решения образуют отрезок длины 1, если  откуда
откуда 
Ответ: 
Приведем другое решение (автор Александр Соколов).
Изобразим решение неравенства  в системе координат
в системе координат ![]()
Прямые  и
и  разбивают плоскость на четыре части, в каждой из которых знаки выражений
разбивают плоскость на четыре части, в каждой из которых знаки выражений  и
и ![]() остаются постоянными.
остаются постоянными.
| знак выражения
| ||||
| знак выражения
| ||||
| соответствующее неравенство |  |  |  |  |
Множество точек, являющееся решением неравенства, на рисунке выделены зелёным цветом.
Очевидно, что решения неравенства образуют отрезок длины 1 ровно два раза.
1 случай: отрезок ограничен прямыми  (слева) и
(слева) и  (справа).
(справа).
Найдём соответствующее значение параметра
 откуда
откуда  и
и 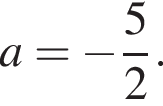
2 случай: отрезок ограничен прямыми 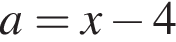 (слева) и
(слева) и  (справа).
(справа).
Найдём соответствующее значение параметра
 откуда
откуда  и
и 
Ответ: 
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен правильный ответ | 4 |
| Либо получен верный ответ, но при его обосновании допущены ошибки, либо обоснованно получен ответ, отличный от верного только из-за потери одного из значений параметра | 3 |
| Ответ неверен, но в решении представлена правильная графическая интерпретация или правильная аналитика | 2 |
| Ответ, возможно, отсутствует или неверен, но в решении с помощью верного рассуждения найдены промежутки, содержащие правильные значения параметра | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |



 образуют отрезок длины 1.
образуют отрезок длины 1.
 и
и 


 откуда
откуда 
 откуда
откуда 
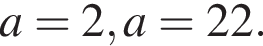
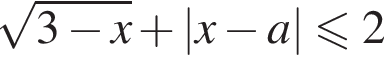

 является часть параболы, она выделена на рисунке цветом океанской воды. График функции
является часть параболы, она выделена на рисунке цветом океанской воды. График функции  при различных значениях параметра получается сдвигом графика функции
при различных значениях параметра получается сдвигом графика функции  на |а| единиц влево или вправо.
на |а| единиц влево или вправо. график правой части неравенства лежит ниже графика левой части, а значит, неравенство не имеет решений. При
график правой части неравенства лежит ниже графика левой части, а значит, неравенство не имеет решений. При  графики имеют единственную общую точку (изображено пурпурным) и неравенство имеет единственное решение. При
графики имеют единственную общую точку (изображено пурпурным) и неравенство имеет единственное решение. При  решением неравенства является отрезок. При
решением неравенства является отрезок. При  где
где  (выделено древесным цветом) решение снова превратится в один отрезок. При
(выделено древесным цветом) решение снова превратится в один отрезок. При  решение остается отрезком, пока, при
решение остается отрезком, пока, при 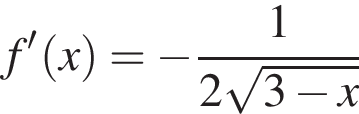 в точке касания
в точке касания 
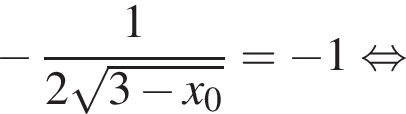





 или
или 

 и прямая
и прямая  являющаяся правым лучом графика функции
являющаяся правым лучом графика функции  имеют ровно одну общую точку. Абсцисса x0 этой точки определяется из уравнения:
имеют ровно одну общую точку. Абсцисса x0 этой точки определяется из уравнения:





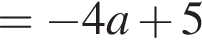

 Найденному значению параметра соответствует уравнение
Найденному значению параметра соответствует уравнение  то есть
то есть 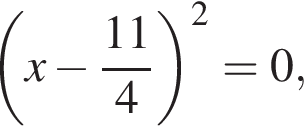 откуда определяем абсциссу точки касания
откуда определяем абсциссу точки касания  При возведении в квадрат уравнения
При возведении в квадрат уравнения 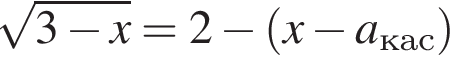 могли появиться посторонние корни, поэтому необходима проверка. Подставляя найденные значения
могли появиться посторонние корни, поэтому необходима проверка. Подставляя найденные значения 


 тогда задача сводится к исследованию неравенства
тогда задача сводится к исследованию неравенства





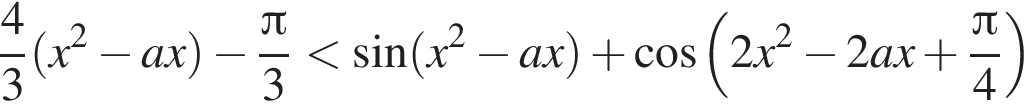



 тогда
тогда  то есть
то есть  Проявив опыт и смекалку, запишем полученное неравенство в виде
Проявив опыт и смекалку, запишем полученное неравенство в виде




 для
для  Поскольку
Поскольку  для всех y, функция f возрастающая. Следовательно, неравенство относительно значений функции можно заменить равносильным неравенством на аргументы. Тогда
для всех y, функция f возрастающая. Следовательно, неравенство относительно значений функции можно заменить равносильным неравенством на аргументы. Тогда  откуда
откуда 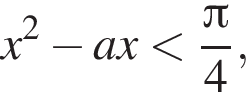 то есть
то есть  которое должно быть выполнено для всех х из отрезка
которое должно быть выполнено для всех х из отрезка  положителен, поэтому если значения g на концах отрезка отрицательны, то и на всем отрезке отрицательны. Получаем систему:
положителен, поэтому если значения g на концах отрезка отрицательны, то и на всем отрезке отрицательны. Получаем систему: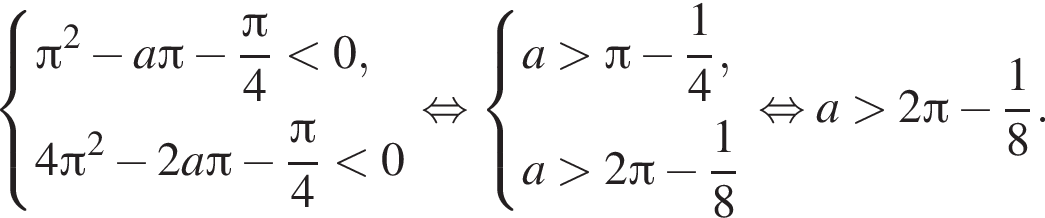

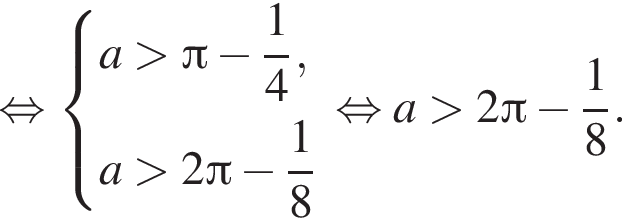
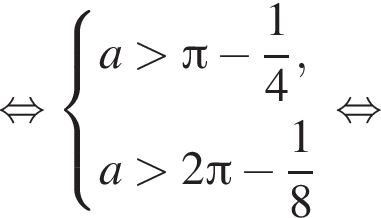


 получим неравенство
получим неравенство  Запишем это неравенство в виде
Запишем это неравенство в виде  Этим задача сведена к неравенству
Этим задача сведена к неравенству  для возрастающей функции
для возрастающей функции  Таким образом,
Таким образом,  откуда
откуда 
 Тогда если
Тогда если  то
то  на всем отрезке
на всем отрезке  откуда
откуда 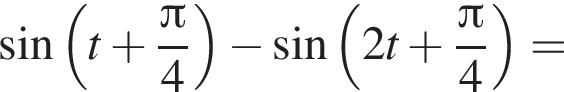


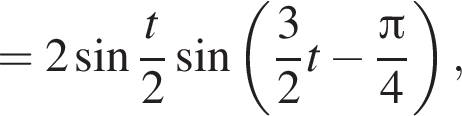

 то
то  Все такие числа t являются решениями, поскольку правая часть не меньше −2.
Все такие числа t являются решениями, поскольку правая часть не меньше −2. то левая часть отрицательна, а правая положительна. Неравенство верно.
то левая часть отрицательна, а правая положительна. Неравенство верно. 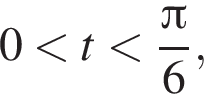 то левая часть положительна, а правая отрицательна. Решений нет.
то левая часть положительна, а правая отрицательна. Решений нет. то в силу неравенства
то в силу неравенства  справедливого для положительных α, получаем:
справедливого для положительных α, получаем:
 В этом случае решений нет, поскольку правая часть не больше 2.
В этом случае решений нет, поскольку правая часть не больше 2.  и далее как ранее.
и далее как ранее.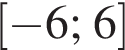 при которых неравенство
при которых неравенство  выполняется при любых
выполняется при любых 



 является вертикальная прямая, графиком уравнения
является вертикальная прямая, графиком уравнения  является гипербола с асимптотами
является гипербола с асимптотами 
 Для построения гиперболы дополнительно составим таблицу:
Для построения гиперболы дополнительно составим таблицу: — верно.
— верно. —
—  — неверно.
— неверно. —
—  — верно.
— верно. —
—  — неверно.
— неверно. —
—  — неверно.
— неверно.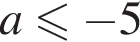 или
или  Учитывая, что по условию
Учитывая, что по условию  получаем ответ (выделено красным).
получаем ответ (выделено красным).




 тогда
тогда



 является решением системы. Значит, при любом положительном значении параметра исходное неравенство имеет решение. Если
является решением системы. Значит, при любом положительном значении параметра исходное неравенство имеет решение. Если 


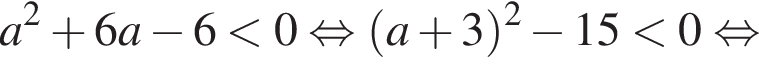
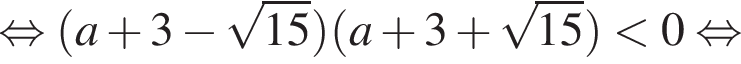





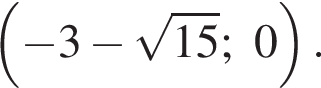

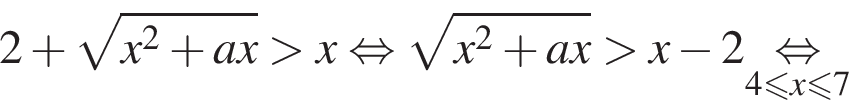




 убывает. Значит, чтобы отрезок
убывает. Значит, чтобы отрезок  необходимо и достаточно, чтобы выполнялось неравенство
необходимо и достаточно, чтобы выполнялось неравенство 


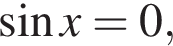 то неравенство верно при любом значении параметра a. Рассмотрим случай
то неравенство верно при любом значении параметра a. Рассмотрим случай 

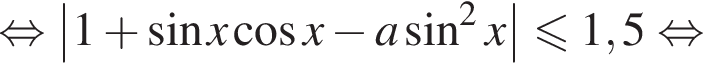





 и первое, и второе неравенства системы имеют решения для любого значения переменной, удовлетворяющего условию
и первое, и второе неравенства системы имеют решения для любого значения переменной, удовлетворяющего условию  причем правая часть второго неравенства не меньше правой части первого, а потому и вся система в целом имеет решения.
причем правая часть второго неравенства не меньше правой части первого, а потому и вся система в целом имеет решения. 

 Это часть плоскости между двумя параболами с разнонаправленными ветвями. Параметр принимает значения от ординаты нижней вершины до ординаты верхней, поэтому
Это часть плоскости между двумя параболами с разнонаправленными ветвями. Параметр принимает значения от ординаты нижней вершины до ординаты верхней, поэтому 

 Тогда
Тогда  и неравенство принимает вид
и неравенство принимает вид

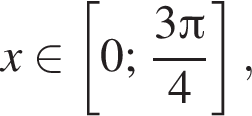 то
то  поэтому достаточно найти все а, при каждом из которых неравенство
поэтому достаточно найти все а, при каждом из которых неравенство





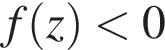 при всех
при всех  тогда и только тогда, когда
тогда и только тогда, когда  Решим эту систему:
Решим эту систему:





 или
или  или
или  или
или


 и
и  также соответствуют решениям. Найдем наибольшее из значений параметра при
также соответствуют решениям. Найдем наибольшее из значений параметра при  Таким образом, в рассматриваемом случае решения есть при каждом значении
Таким образом, в рассматриваемом случае решения есть при каждом значении 

 и
и  получим:
получим:  Таким образом, в рассматриваемом случае решения есть при каждом значении
Таким образом, в рассматриваемом случае решения есть при каждом значении 



 то на ОДЗ неравенство верно.
то на ОДЗ неравенство верно. то
то



 исходное неравенство имеет два решения;
исходное неравенство имеет два решения; — бесконечное число решений;
— бесконечное число решений;
 то
то  или
или  то
то  то
то  или
или  или
или  то
то  или
или  то
то 
 то
то 


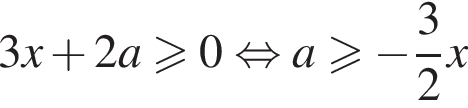
 включая эту прямую.
включая эту прямую.

 — верно.
— верно. — неверно.
— неверно. неравенство имеет одно решение, при
неравенство имеет одно решение, при  неравенство имеет бесконечное число решений, при
неравенство имеет бесконечное число решений, при 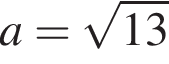 неравенство имеет два решения, при
неравенство имеет два решения, при  неравенство имеет одно решение.
неравенство имеет одно решение.
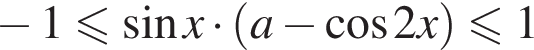



 и
и  Введём функцию
Введём функцию  где
где 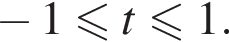 Тогда нужно, чтобы неравенство
Тогда нужно, чтобы неравенство

 значит, условие (⁎) не выполняется при всех t из отрезка
значит, условие (⁎) не выполняется при всех t из отрезка  тогда
тогда 



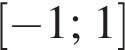 в двух случаях.
в двух случаях. то достаточно выполнения условий
то достаточно выполнения условий
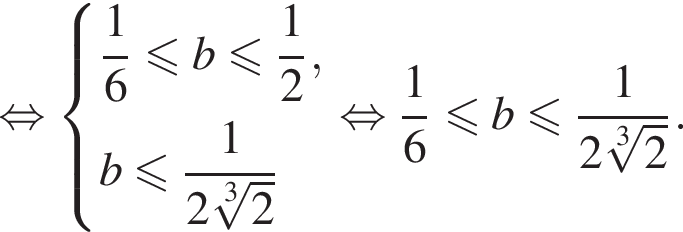




 то достаточно выполнения условий
то достаточно выполнения условий
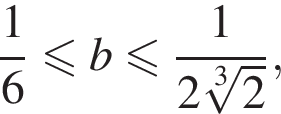 то есть если
то есть если  Вернёмся к исходному параметру:
Вернёмся к исходному параметру:




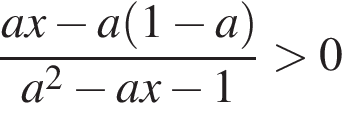





 прямая, проходящая через точки
прямая, проходящая через точки 
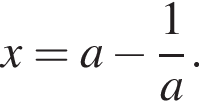
 нечётная, ее производная
нечётная, ее производная  положительна при всех
положительна при всех 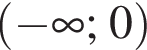 и на
и на  График имеет асимптоты
График имеет асимптоты  (выделены оранжевым пунктиром) разбивают плоскость на восемь областей, в каждой из которых знак левой части исходного неравенства остается неизменным. Подставляя координаты какой-либо точки из каждой области, проверяем выполнение исходного неравенства. Области, в которых неравенство выполняется, выделены на рисунке светло-зеленым цветом.
(выделены оранжевым пунктиром) разбивают плоскость на восемь областей, в каждой из которых знак левой части исходного неравенства остается неизменным. Подставляя координаты какой-либо точки из каждой области, проверяем выполнение исходного неравенства. Области, в которых неравенство выполняется, выделены на рисунке светло-зеленым цветом.  (выделены синим). Значения x, которые не превосходят по модулю 1, находятся внутри полосы, ограниченной этими прямыми, включая сами прямые. Тогда исходное неравенство выполняется для любых x, не превосходящих по модулю 1, при
(выделены синим). Значения x, которые не превосходят по модулю 1, находятся внутри полосы, ограниченной этими прямыми, включая сами прямые. Тогда исходное неравенство выполняется для любых x, не превосходящих по модулю 1, при  где a1 — меньший корень уравнения
где a1 — меньший корень уравнения  а a2 — корень уравнения
а a2 — корень уравнения  Ясно, что
Ясно, что  Найдём a1:
Найдём a1:





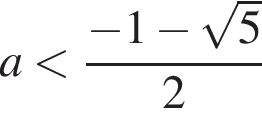 и
и 
 выполняется при любых x.
выполняется при любых x.


 тогда получим систему
тогда получим систему
 и
и  положительно, а голубым цветом те, в которых отрицательно). Анализируя график, получаем, что неравенство выполняется при любых значениях x тогда и только тогда, когда
положительно, а голубым цветом те, в которых отрицательно). Анализируя график, получаем, что неравенство выполняется при любых значениях x тогда и только тогда, когда 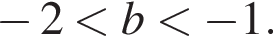 Возвращаясь к параметру a, получаем
Возвращаясь к параметру a, получаем 
