1. Тип 18 № 507235 

Классификатор алгебры: Расположение корней квадратного трехчлена
Методы алгебры: Введение замены, Группировка, Метод интервалов
Задача с параметром. Расположение корней квадратного трехчлена
i
Найдите все значения параметра а, при каждом из которых множество решений неравенства

содержит отрезок 
Решение. Заметим, что при любых значениях переменной x и параметра a знаменатель дроби в левой части неравенства положителен, поэтому исходное неравенство равносильно неравенству





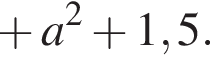
Для того чтобы множество решений неравенства содержало отрезок  синус должен принимать все значения
синус должен принимать все значения  (см. рис.)
(см. рис.)
Пусть  тогда неравенство принимает вид
тогда неравенство принимает вид


Рассмотрим функцию  Для того, чтобы множество решений последнего неравенства содержало отрезок
Для того, чтобы множество решений последнего неравенства содержало отрезок ![]() необходимо и достаточно, чтобы одновременно выполнялись два условия
необходимо и достаточно, чтобы одновременно выполнялись два условия  и
и 






Ответ: 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 4 |
| С помощью верного рассуждения получены все верные значения параметра, но решение недостаточно обосновано | 3 |
| С помощью верного рассуждения получен промежуток, содержащий верный ответ, либо содержащийся в верном промежутке | 2 |
| Задача сведена к исследованию взаимного расположения частей двух парабол | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ответ: 

507235

Классификатор алгебры: Расположение корней квадратного трехчлена
Методы алгебры: Введение замены, Группировка, Метод интервалов
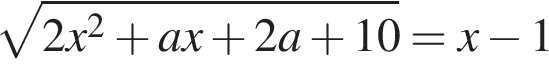 не имеет действительных корней.
не имеет действительных корней.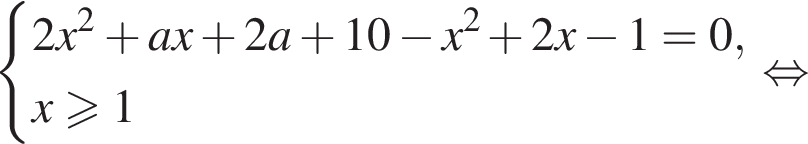





 имеет решения, каждое из которых меньше 1. Рассмотрим функцию
имеет решения, каждое из которых меньше 1. Рассмотрим функцию  необходимо и достаточно одновременного выполнения неравенств:
необходимо и достаточно одновременного выполнения неравенств: 
 Получаем:
Получаем: 





 Если
Если  — два корня. Если
— два корня. Если  — единственный корень.
— единственный корень.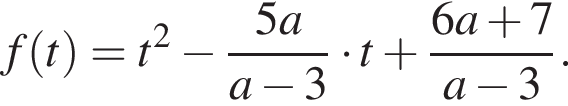 Исходное уравнение имеет ровно два корня тогда и только тогда, когда уравнение
Исходное уравнение имеет ровно два корня тогда и только тогда, когда уравнение  имеет корни, из которых ровно один больше 1, и при этом
имеет корни, из которых ровно один больше 1, и при этом  имеет ровно один корень, если дискриминант равен нулю:
имеет ровно один корень, если дискриминант равен нулю:



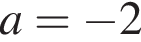 уравнение
уравнение  имеет единственный корень
имеет единственный корень  уравнение
уравнение  имеет единственный корень
имеет единственный корень 


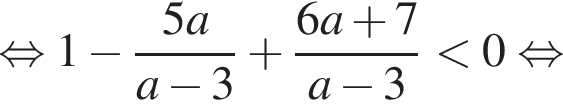

 Ответ отличается от верного только включением точек
Ответ отличается от верного только включением точек  или
или 
 Если
Если  и
и  Если
Если 
 Исходное уравнение имеет ровно два корня в двух случаях:
Исходное уравнение имеет ровно два корня в двух случаях: имеет ровно один корень, если дискриминант равен нулю:
имеет ровно один корень, если дискриминант равен нулю:



 имеет единственный корень
имеет единственный корень 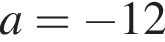 уравнение
уравнение  имеет единственный корень
имеет единственный корень 




 Ответ отличается от верного только включением точек
Ответ отличается от верного только включением точек 













 Этот случай невозможен. Действительно, пусть
Этот случай невозможен. Действительно, пусть 




 верно для всех x из отрезка [0; 1,5].
верно для всех x из отрезка [0; 1,5].
 В правой части — линейная функция с отрицательным угловым коэффициентом. Для того, чтобы на отрезке [0; 1,5] прямая лежала ниже графика корня, значение линейной функции при x = 0 должно быть меньше 5, а при x = 1,5 должно быть меньше 10. Решая систему неравенств
В правой части — линейная функция с отрицательным угловым коэффициентом. Для того, чтобы на отрезке [0; 1,5] прямая лежала ниже графика корня, значение линейной функции при x = 0 должно быть меньше 5, а при x = 1,5 должно быть меньше 10. Решая систему неравенств 
 находим, что
находим, что 
 тогда
тогда  Имеем:
Имеем:

 соответствуют t, лежащие в отрезке
соответствуют t, лежащие в отрезке  неравенство (⁎) верно, поскольку на отрезке
неравенство (⁎) верно, поскольку на отрезке 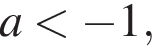 то старший коэффициент квадратичной функции
то старший коэффициент квадратичной функции  отрицателен, а потому для того, чтобы функция f была положительной на
отрицателен, а потому для того, чтобы функция f была положительной на  и
и  Тогда
Тогда  и
и  то есть
то есть 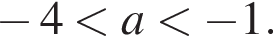 Объединяя со случаем
Объединяя со случаем 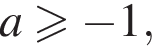 окончательно получаем:
окончательно получаем: 
 поэтому
поэтому  Задачу можно сформулировать так: найдите значения a, при каждом из которых уравнение
Задачу можно сформулировать так: найдите значения a, при каждом из которых уравнение  имеет хотя бы одно решение, удовлетворяющее условию
имеет хотя бы одно решение, удовлетворяющее условию 


 не является корнем уравнения.
не является корнем уравнения. Её график — парабола, ветви которой направлены вверх. Следовательно, условие задачи выполнено тогда и только тогда, когда выполняется одно из трех условий:
Её график — парабола, ветви которой направлены вверх. Следовательно, условие задачи выполнено тогда и только тогда, когда выполняется одно из трех условий:


 — абсцисса вершины параболы. Эти условия соответствуют следующим способам расположения графика функции
— абсцисса вершины параболы. Эти условия соответствуют следующим способам расположения графика функции 


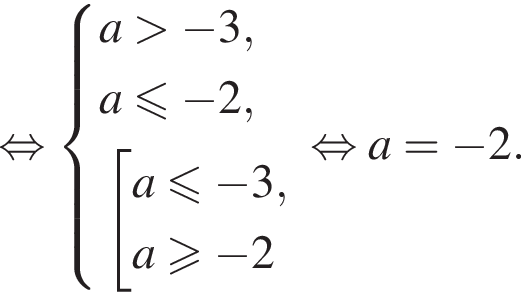
 поэтому
поэтому  и преобразуем уравнение.
и преобразуем уравнение. 

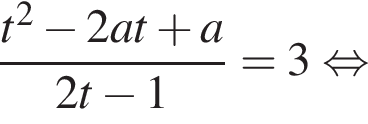

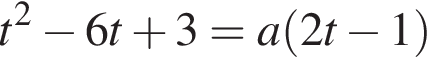 имеет хотя бы одно решение, удовлетворяющее условию
имеет хотя бы одно решение, удовлетворяющее условию  Левая часть этого уравнения — функция
Левая часть этого уравнения — функция  графиком которой является парабола, правая часть — функция
графиком которой является парабола, правая часть — функция  пучок прямых, проходящих через точку
пучок прямых, проходящих через точку  Для того чтобы исходное уравнение имело решение, необходимо, чтобы графики пересекались при
Для того чтобы исходное уравнение имело решение, необходимо, чтобы графики пересекались при 

 должен быть равен нулю.
должен быть равен нулю. 
 — графики пересекаются на промежутке
— графики пересекаются на промежутке  при
при  — графики не пересекаются, при
— графики не пересекаются, при  — графики пересекаются на промежутке
— графики пересекаются на промежутке 
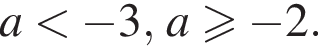
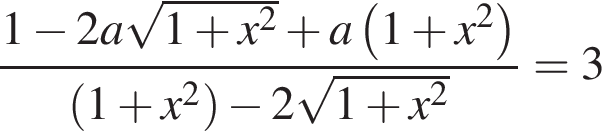
 Исходное уравнение имеет хотя бы одно решение тогда и только тогда, когда имеет хотя бы одно решение система
Исходное уравнение имеет хотя бы одно решение тогда и только тогда, когда имеет хотя бы одно решение система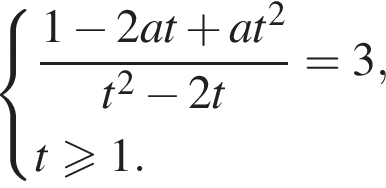


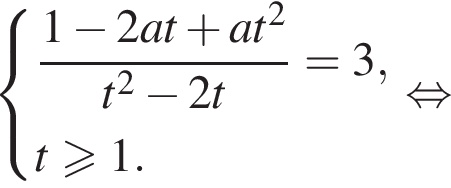









 Из неравенства
Из неравенства  следует, что
следует, что  Имеем:
Имеем:  Теперь задачу можно сформулировать так: найдите все значения а, при каждом из которых уравнение
Теперь задачу можно сформулировать так: найдите все значения а, при каждом из которых уравнение  имеет хотя бы одно решение, удовлетворяющее условию
имеет хотя бы одно решение, удовлетворяющее условию 


 Её график — парабола, ветви которой направлены вверх. Следовательно, условие задачи выполнено тогда и только тогда, когда выполняется одно из трех условий:
Её график — парабола, ветви которой направлены вверх. Следовательно, условие задачи выполнено тогда и только тогда, когда выполняется одно из трех условий: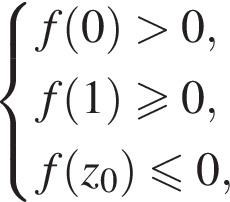



 При
При 




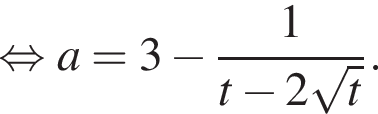





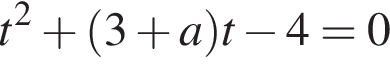 имеет хотя бы один корень, принадлежащий отрезку [−1; 1]. Графиком функции
имеет хотя бы один корень, принадлежащий отрезку [−1; 1]. Графиком функции  является парабола, ветви которой направлены вверх,
является парабола, ветви которой направлены вверх, 
 (рис. 1)
(рис. 1)  откуда
откуда  либо при условии
либо при условии  (рис. 2)
(рис. 2)  откуда
откуда 



 косинус должен принимать значения
косинус должен принимать значения  (см. рис.)
(см. рис.) тогда
тогда  и неравенство принимает вид
и неравенство принимает вид (2)
(2) (3)
(3)





 удвоенный аргумент должен содержать отрезок
удвоенный аргумент должен содержать отрезок  а косинус двойного угла должен принимать все значения
а косинус двойного угла должен принимать все значения  (см. рис.).
(см. рис.). тогда неравенство принимает вид
тогда неравенство принимает вид


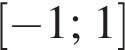 необходимо и достаточно, чтобы одновременно выполнялись два условия
необходимо и достаточно, чтобы одновременно выполнялись два условия  и
и 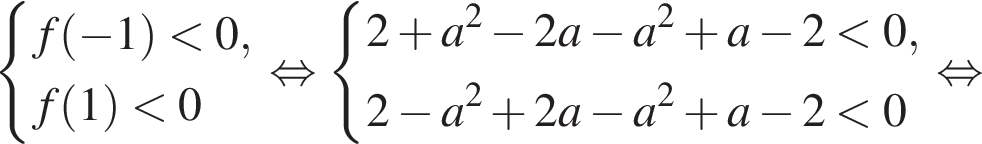




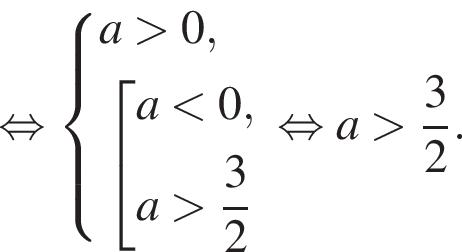




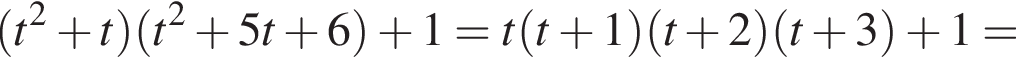








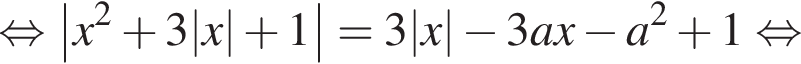


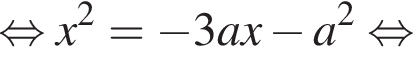

 Это квадратичная функция, графиком которой является парабола, ветви которой направлены вверх. Следовательно, для того, чтобы уравнение
Это квадратичная функция, графиком которой является парабола, ветви которой направлены вверх. Следовательно, для того, чтобы уравнение  а значит, и исходное уравнение, имело корни как большие −3, так и меньшие −3, необходимо и достаточно, чтобы
а значит, и исходное уравнение, имело корни как большие −3, так и меньшие −3, необходимо и достаточно, чтобы  Решим это неравенство:
Решим это неравенство:














 тогда
тогда  Для того, чтобы исходное неравенство было выполнено при любом значении x, необходимо и достаточно, чтобы неравенство
Для того, чтобы исходное неравенство было выполнено при любом значении x, необходимо и достаточно, чтобы неравенство  было выполнено для всех
было выполнено для всех 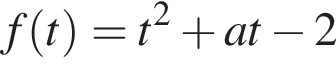 с положительным старшим коэффициентом, эскиз графика которой приведен на рисунке. Для выполнения условия задачи необходимо и достаточно, чтобы выполнялась система
с положительным старшим коэффициентом, эскиз графика которой приведен на рисунке. Для выполнения условия задачи необходимо и достаточно, чтобы выполнялась система 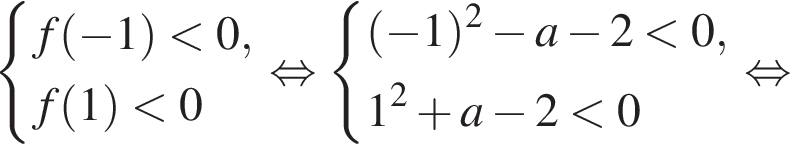






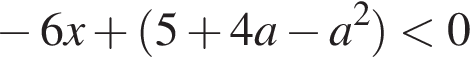




 выполнялось хотя бы при при одном значении а, принадлежащем отрезку
выполнялось хотя бы при при одном значении а, принадлежащем отрезку 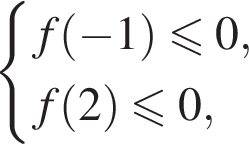











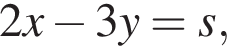
 тогда
тогда  Получаем систему
Получаем систему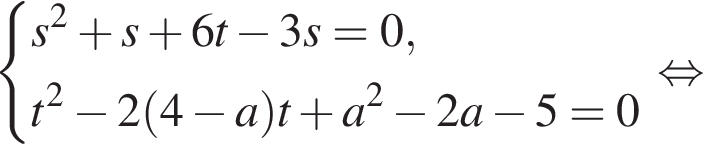

 тогда система имеет решения в том случае, когда уравнение
тогда система имеет решения в том случае, когда уравнение  имеет хотя бы один корень, удовлетворяющий условию
имеет хотя бы один корень, удовлетворяющий условию 

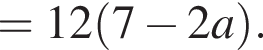


 Графиком является парабола, ветви которой направлены вверх, абсцисса вершины
Графиком является парабола, ветви которой направлены вверх, абсцисса вершины  При
При 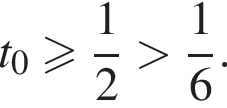 Значит, только один (меньший) корень уравнения
Значит, только один (меньший) корень уравнения 







 где
где 


 Для того чтобы исходное уравнение имело ровно два корня, хотя бы один из которых не менее 0,5, уравнение
Для того чтобы исходное уравнение имело ровно два корня, хотя бы один из которых не менее 0,5, уравнение  должно иметь два положительных корня, хотя бы один из которых не больше
должно иметь два положительных корня, хотя бы один из которых не больше  или
или 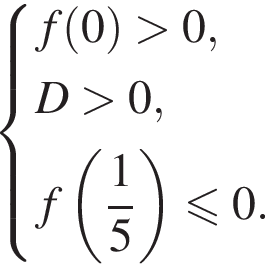

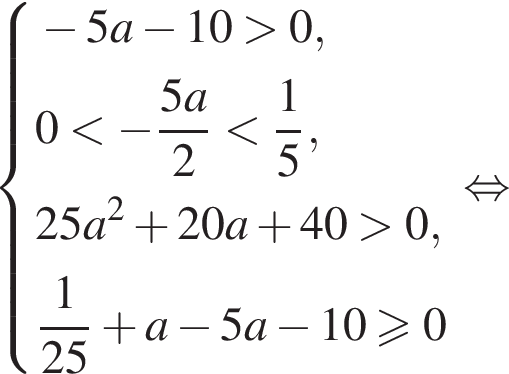








 При
При 


 Значит, уравнение имеет ровно два корня
Значит, уравнение имеет ровно два корня 
 является парабола с ветвями, направленными вверх, и вершиной в точке
является парабола с ветвями, направленными вверх, и вершиной в точке 
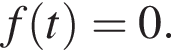 Поскольку
Поскольку  неравенства
неравенства  и
и  Получаем:
Получаем:  и
и 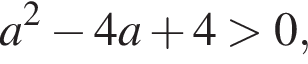 следовательно,
следовательно, 

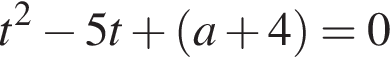 при условиях
при условиях