1. Тип Д8 C1 № 507570 

Классификатор алгебры: Основное тригонометрическое тождество и его следствия, Системы тригонометрических уравнений
Уравнения, системы уравнений. Системы тригонометрических уравнений
i
Решите систему 
Решение. Из второго уравнения находим:  Учитывая, что
Учитывая, что  получаем систему уравнений:
получаем систему уравнений:









Ответ: 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а или пункте б, ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения уравнения и отбора корней | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
Ответ: 

507570



 или
или 
 то
то  тогда
тогда  Это невозможно.
Это невозможно. то
то  тогда
тогда  Это невозможно.
Это невозможно.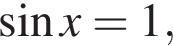 то
то  тогда
тогда 


 откуда
откуда  Значит,
Значит, 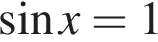 или
или 
 то второе уравнение не имеет решений. При
то второе уравнение не имеет решений. При  рассмотрим второе уравнение как квадратное относительно
рассмотрим второе уравнение как квадратное относительно 
 отрицательно при всех возможных x, значит,
отрицательно при всех возможных x, значит,  Следовательно, случай
Следовательно, случай  находим:
находим: 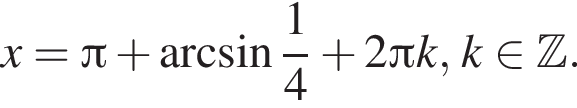
 Второе уравнение принимает вид:
Второе уравнение принимает вид:  откуда:
откуда:  Значит,
Значит, 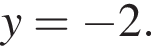


 откуда
откуда  Учитывая, что
Учитывая, что  Тогда
Тогда 

 или
или 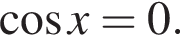 Последнее равносильно
Последнее равносильно  Тогда
Тогда  что невозможно.
что невозможно.  Тогда
Тогда 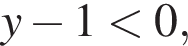 что невозможно.
что невозможно.



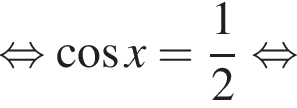


 не удовлетворяет уравнению (*).
не удовлетворяет уравнению (*).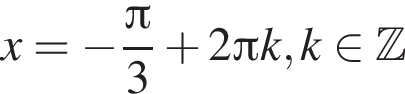 удовлетворяет уравнению (*).
удовлетворяет уравнению (*).

















 то
то  при этом из второго уравнения следует, что
при этом из второго уравнения следует, что 
 то из первого уравнения находим:
то из первого уравнения находим: 
 учитывая условие
учитывая условие 


 находим:
находим:  или
или 
 тогда либо
тогда либо  и
и 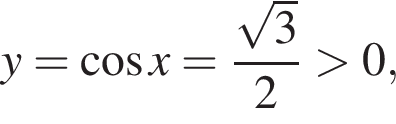 либо
либо  и
и  — не дает решения.
— не дает решения. тогда
тогда  — не дает решения.
— не дает решения.

 находим:
находим:  и
и  либо
либо 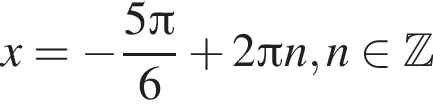 и
и 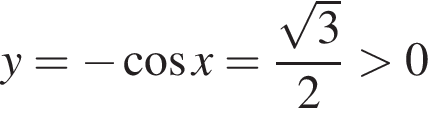 — не дает решения.
— не дает решения. — не дает решения.
— не дает решения.


 или
или  тогда
тогда 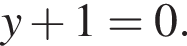
 тогда
тогда  Это невозможно.
Это невозможно. тогда
тогда  и в этом случае получаются решения системы.
и в этом случае получаются решения системы.




 тогда получим:
тогда получим: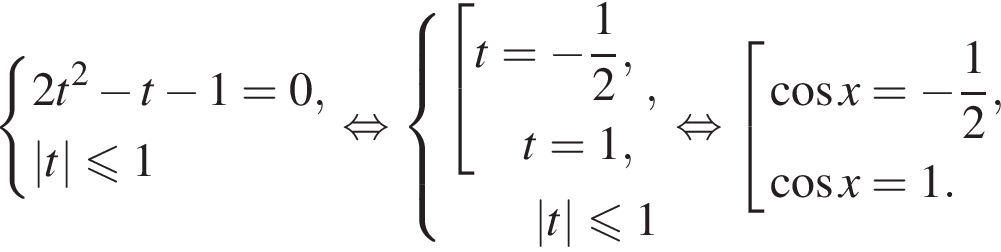




 Тогда
Тогда  И из второго уравнения получаем:
И из второго уравнения получаем:  откуда
откуда 
 Из второго уравнения следует, что
Из второго уравнения следует, что  Тогда
Тогда  откуда
откуда  а из второго уравнения получаем:
а из второго уравнения получаем:  откуда
откуда 


 откуда
откуда  или
или  Из второго уравнения следует, что
Из второго уравнения следует, что  Таким образом,
Таким образом,  Рассмотрим оставшиеся случаи.
Рассмотрим оставшиеся случаи. Тогда
Тогда 
 Тогда
Тогда 

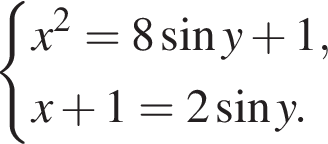



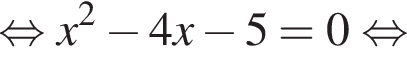

 из второго уравнения следует:
из второго уравнения следует:  откуда
откуда 
 Решений нет.
Решений нет.




 из второго уравнения получаем:
из второго уравнения получаем:  откуда
откуда 
 Нет решений.
Нет решений.

 Получаем:
Получаем:

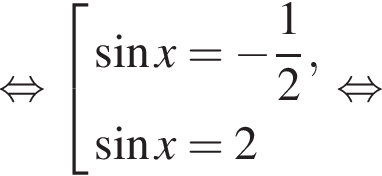



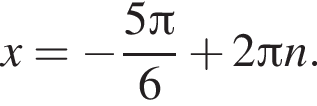 Второе уравнение принимает вид
Второе уравнение принимает вид  откуда
откуда 


 тогда
тогда


 не имеет решений. Из первого уравнения следует, что
не имеет решений. Из первого уравнения следует, что  Из уравнения
Из уравнения  находим, что
находим, что 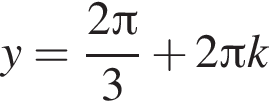 или
или  Условию
Условию  удовлетворяет только
удовлетворяет только  Следовательно,
Следовательно,  откуда
откуда  и, значит,
и, значит, 
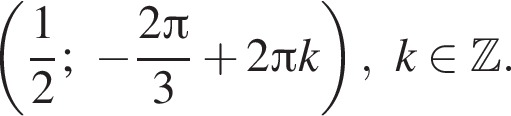

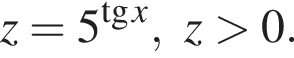 Тогда
Тогда 

 значит,
значит,  Поэтому
Поэтому  Тогда
Тогда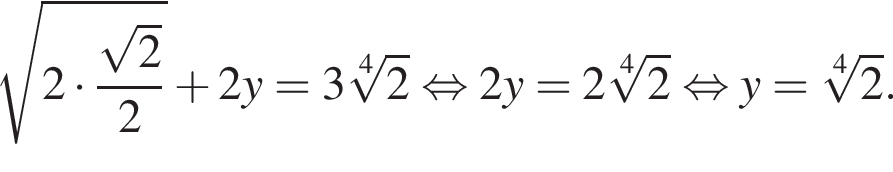


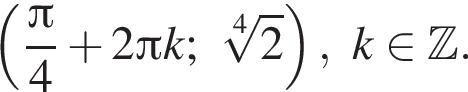

 Тогда уравнение примет вид:
Тогда уравнение примет вид:
 не имеет решений. Из уравнения
не имеет решений. Из уравнения 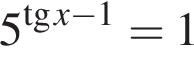 находим:
находим:  откуда
откуда 
 значит,
значит,  Поэтому
Поэтому 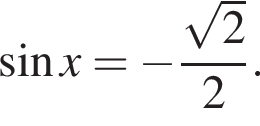 Найдём y из второго уравнения:
Найдём y из второго уравнения:












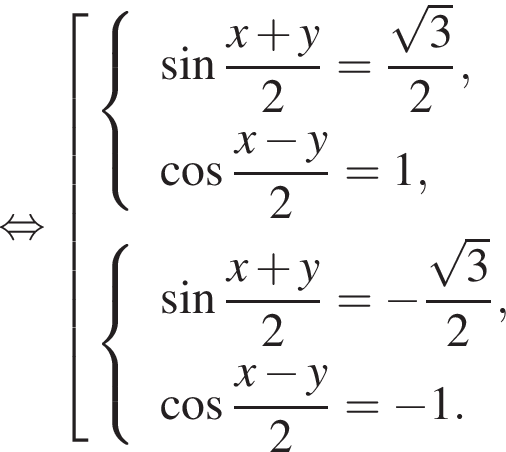
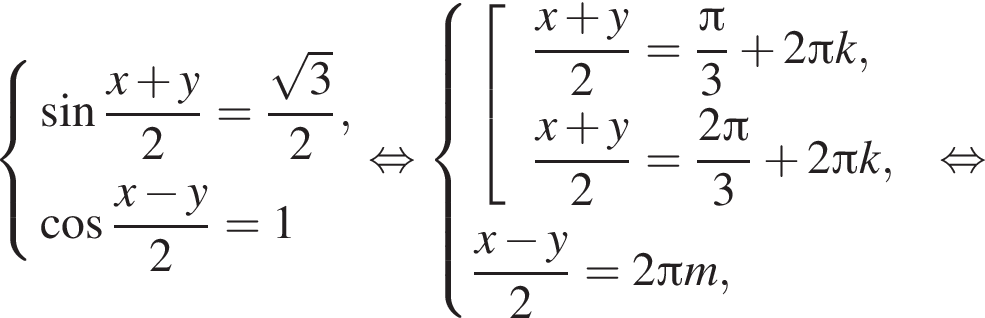









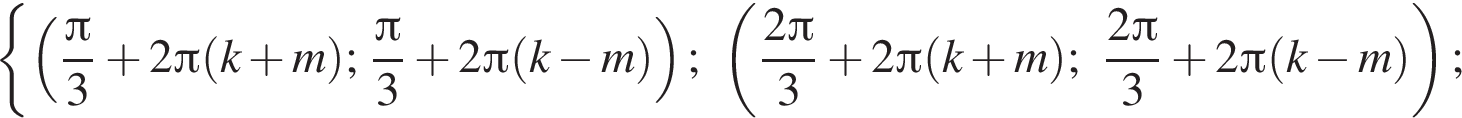


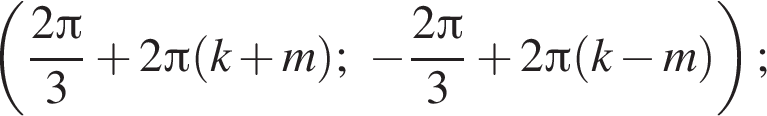
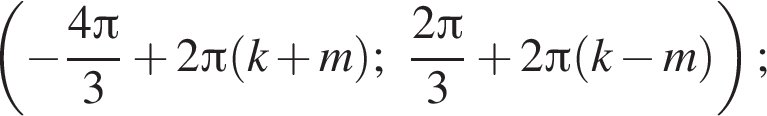
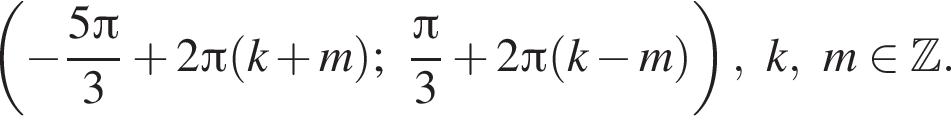








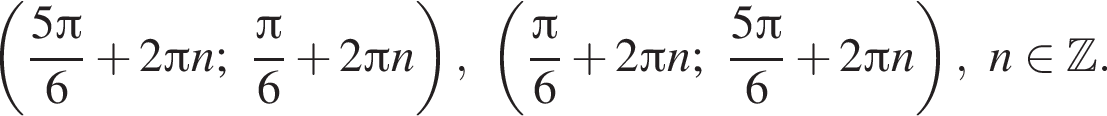

 или
или 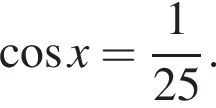
 то из первого уравнения
то из первого уравнения  Уравнение не имеет решений. Если
Уравнение не имеет решений. Если  то
то  и из первого уравнения получаем:
и из первого уравнения получаем: 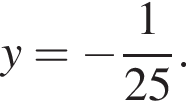


 получаем
получаем 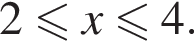
 тогда
тогда  если
если  Из второго уравнения получаем
Из второго уравнения получаем  откуда
откуда  или
или  Значит, первое решение системы
Значит, первое решение системы 
 Тогда
Тогда  и поэтому из первого уравнения получаем:
и поэтому из первого уравнения получаем: 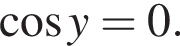
 Тогда
Тогда  Из всех решений уравнения
Из всех решений уравнения  этому условию удовлетворяет только
этому условию удовлетворяет только  При этом
При этом 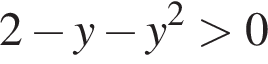 и, из второго уравнения получаем:
и, из второго уравнения получаем:  Из всех решений этого уравнения интервалу
Из всех решений этого уравнения интервалу 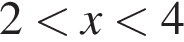 принадлежит только
принадлежит только 
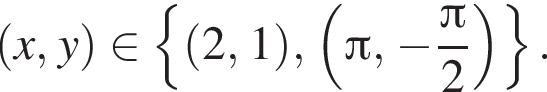



 Разложим выражение
Разложим выражение  как сумму кубов квадратов:
как сумму кубов квадратов: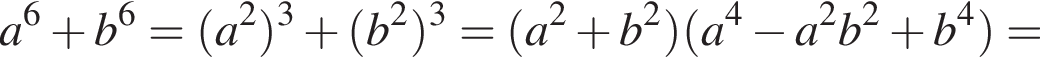



 тогда
тогда


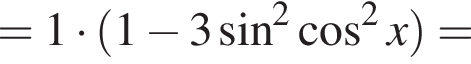

 Находим:
Находим:








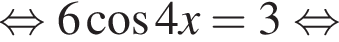
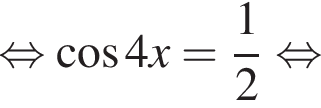



 найдем перебором. При
найдем перебором. При 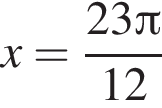 — не лежит на данном отрезке — или
— не лежит на данном отрезке — или  — лежит на данном отрезке. При
— лежит на данном отрезке. При  и
и  лежащие на заданном отрезке. При
лежащие на заданном отрезке. При  — не лежит на данном отрезке — или
— не лежит на данном отрезке — или  — лежит на данном отрезке. При
— лежит на данном отрезке. При 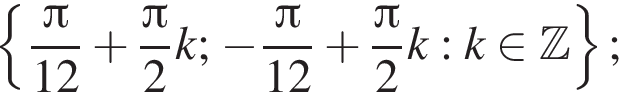 б)
б)