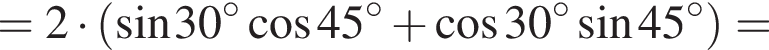Параллелограмм и окружность расположены так, что сторона AB касается окружности, CD является хордой, а стороны DA и BC пересекают окружность в точках P и Q соответственно.
а) Докажите, что около четырехугольника ABQP можно описать окружность.
б) Найдите длину отрезка DQ, если известно, что AP = a, BC = b, BQ = c.
Решение. а) Четырехугольник CDPQ вписан в окружность, и его стороны PD и CQ параллельны, следовательно, CDPQ ― либо прямоугольник, либо равнобедренная трапеция, откуда PQ = CD, но CD = AB, значит, и четырехугольник ABQP ― также прямоугольник или равнобедренная трапеция, и, следовательно, около него можно описать окружность, что и требовалось доказать.
б) Поскольку AK — касательная к данной окружности, а AD ― секущая, имеем: Аналогично находим
Аналогично находим  откуда
откуда  и тогда
и тогда 
Пусть QH ― высота равнобедренной трапеции CDPQ. Тогда









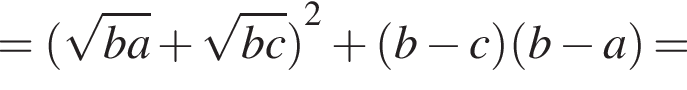


Таким образом, 
Ответ: 
Замечание.
Учащиеся, знающие теорему Птолемея для вписанного четырехугольника, могут привести более короткое решение, сразу написав 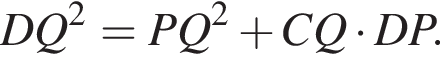
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) ИЛИ имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) ИЛИ при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | 1 |
| Решение не соответствует ни одному из критериев, приведённых выше | 0 |
| Максимальный балл | 3 |




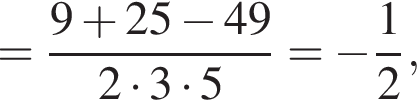






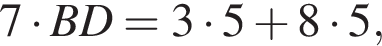

 поскольку
поскольку  Пусть
Пусть  тогда в треугольнике BAD по теореме косинусов
тогда в треугольнике BAD по теореме косинусов















 Заметим, что
Заметим, что  следовательно, CB параллельно FA. Тогда четырехугольник FCBA — вписанная в окружность трапеция, что означает, что она равнобедренная. Поэтому
следовательно, CB параллельно FA. Тогда четырехугольник FCBA — вписанная в окружность трапеция, что означает, что она равнобедренная. Поэтому  Следовательно,
Следовательно,  и CF параллельно BE, ведь соответственные углы
и CF параллельно BE, ведь соответственные углы  Заметим, что
Заметим, что  как вертикальные и
как вертикальные и  как вписанные, опирающиеся на одну дугу. Тогда треугольник CFE — равнобедренный,
как вписанные, опирающиеся на одну дугу. Тогда треугольник CFE — равнобедренный,  Найдем катет BH по теореме Пифагора, он равен
Найдем катет BH по теореме Пифагора, он равен  Найдем DH по теореме о произведении отрезков пересекающихся хорд:
Найдем DH по теореме о произведении отрезков пересекающихся хорд:


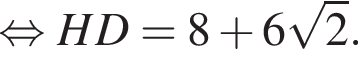
 (площадь дельтоида)
(площадь дельтоида) 


 как накрест лежащие.
как накрест лежащие.
 Следовательно,
Следовательно,  Тогда
Тогда

 из равенства
из равенства  находим, что
находим, что  Следовательно,
Следовательно, 



 По теореме синусов для треугольника ABC находим:
По теореме синусов для треугольника ABC находим:  откуда
откуда











 Треугольник ABC равнобедренный, поэтому
Треугольник ABC равнобедренный, поэтому  Значит,
Значит,  Четырехугольник ABCD — равнобедренная трапеция, поэтому
Четырехугольник ABCD — равнобедренная трапеция, поэтому  Значит,
Значит, 







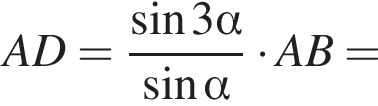

 а из треугольника BOF получаем, что
а из треугольника BOF получаем, что  Тогда высота трапеции
Тогда высота трапеции  а
а 

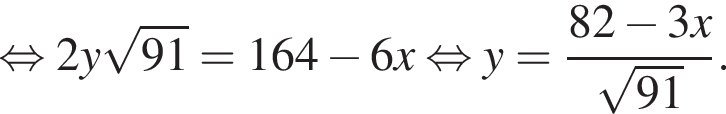



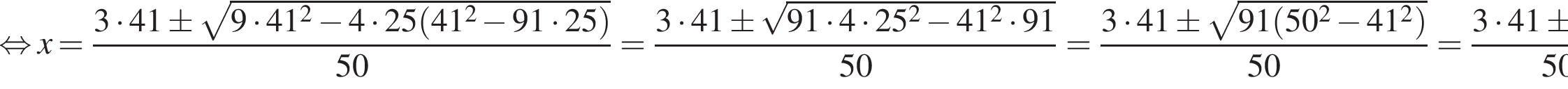

 получим, что треугольники BTC и ATD подобны с коэффициентом 2 : 1, значит,
получим, что треугольники BTC и ATD подобны с коэффициентом 2 : 1, значит,
 Из отношения
Из отношения  найдем, что
найдем, что 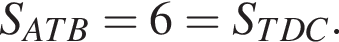 Вычислим площадь трапеции ABCD:
Вычислим площадь трапеции ABCD:
 где h — высота трапеции. Поскольку
где h — высота трапеции. Поскольку 

 Треугольник ABC равнобедренный, поэтому
Треугольник ABC равнобедренный, поэтому  Значит,
Значит, 


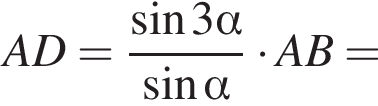

 Тогда
Тогда










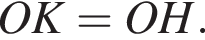
 а значит, KBMH — прямоугольник,
а значит, KBMH — прямоугольник,  Вписанный угол CBM прямой, значит, CM — диаметр окружности. Медиана AO делит треугольник ACM на два треугольника равной площади,
Вписанный угол CBM прямой, значит, CM — диаметр окружности. Медиана AO делит треугольник ACM на два треугольника равной площади,
















 если
если 
 по теореме Пифагора в треугольнике ABC и
по теореме Пифагора в треугольнике ABC и  по теореме Пифагора в треугольнике ABD.
по теореме Пифагора в треугольнике ABD.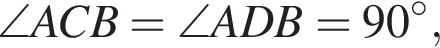 поэтому точки A, B, C, D лежат на одной окружности. Из равенства углов BAC и CAD следует равенство дуг, на которые они опираются. Равные дуги стягиваются равными хордами BC и CD, что и требовалось доказать.
поэтому точки A, B, C, D лежат на одной окружности. Из равенства углов BAC и CAD следует равенство дуг, на которые они опираются. Равные дуги стягиваются равными хордами BC и CD, что и требовалось доказать. как опирающиеся на одну дугу. Из условия следует, что
как опирающиеся на одну дугу. Из условия следует, что



 Из треугольника BTC найдем
Из треугольника BTC найдем 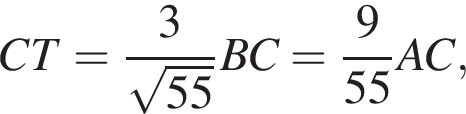 откуда и следует ответ.
откуда и следует ответ. как вписанные. Следовательно,
как вписанные. Следовательно,  поскольку
поскольку 
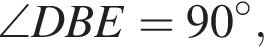 откуда
откуда  Четырехугольник ABEC — равнобокая трапеция, значит,
Четырехугольник ABEC — равнобокая трапеция, значит, 
 следовательно,
следовательно,
 и
и  Тогда:
Тогда:








 На его стороне BC вне треугольника (точки A и D лежат в разных полуплоскостях относительно прямой BC) построим равносторонний треугольник BCD.
На его стороне BC вне треугольника (точки A и D лежат в разных полуплоскостях относительно прямой BC) построим равносторонний треугольник BCD.




 Треугольник BCD равносторонний, в нем угол BDC равен 60°. Тогда
Треугольник BCD равносторонний, в нем угол BDC равен 60°. Тогда  а потому четырехугольник ABDC вписан в окружность.
а потому четырехугольник ABDC вписан в окружность.






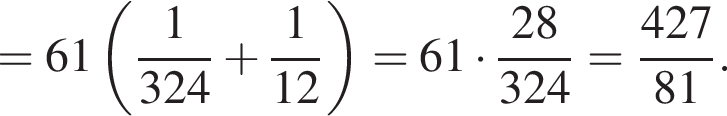
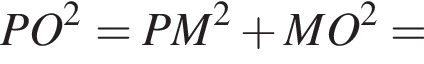



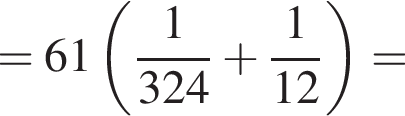



 следовательно, и треугольник BOC равносторонний, то есть
следовательно, и треугольник BOC равносторонний, то есть  и тогда
и тогда 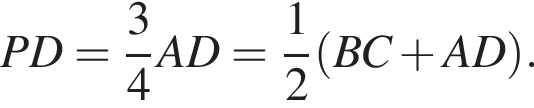
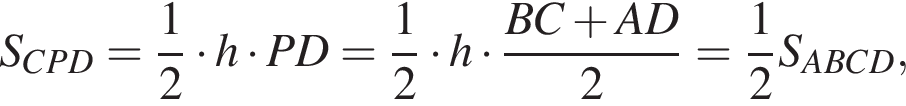





 По теореме о произведении отрезков хорд получаем:
По теореме о произведении отрезков хорд получаем:  то есть
то есть  откуда
откуда  Тогда
Тогда



 получаем:
получаем:  Таким образом,
Таким образом,
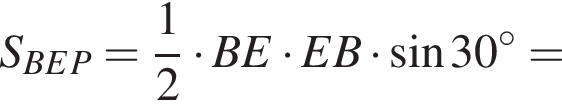

 откуда следует равенство треугольников KPE и KCE и отрезков PE и CE как соответственных элементов. Аналогично равны треугольники DPE и QCE и отрезки DP и CQ. Заметим, что
откуда следует равенство треугольников KPE и KCE и отрезков PE и CE как соответственных элементов. Аналогично равны треугольники DPE и QCE и отрезки DP и CQ. Заметим, что



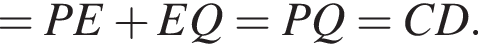

 Прямая AF пересекает сторону ВС в точке Т, а диагональ BD — в точке О.
Прямая AF пересекает сторону ВС в точке Т, а диагональ BD — в точке О.



 Пусть радиус окружности равен R. По теореме синусов получаем
Пусть радиус окружности равен R. По теореме синусов получаем  Далее
Далее  то есть
то есть  Тогда
Тогда

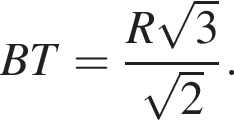




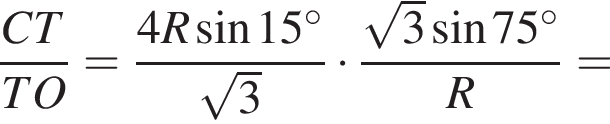




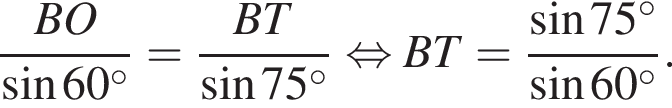
 Следовательно,
Следовательно,