
Решите неравенство



Решение. Сделаем замену:  Тогда
Тогда






Неравенство принимает вид:  откуда
откуда

Это неравенство выполняется тогда и только тогда, когда ![]() Получаем:
Получаем:






Ответ: ![]()
Примечание.
Задача допускает решение без замены переменной: тождественными преобразованиями данное неравенство приводится к  откуда также получается ответ
откуда также получается ответ 
Приведем решение Наиля Мусина для нахождения нулей числителя.
Выполним преобразования:



Для нахождения нулей числителя сделаем замену 
 Заметим, что
Заметим, что


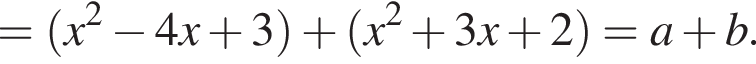



Для нахождения нулей числителя решим уравнение:

Возвращаясь к исходным переменным, получим

| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 2 |
| Обоснованно получен ответ, отличающийся от верного исключением точек, ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |





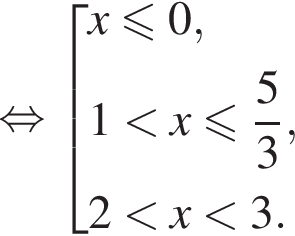





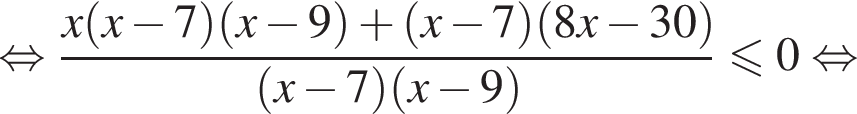


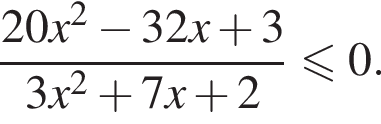







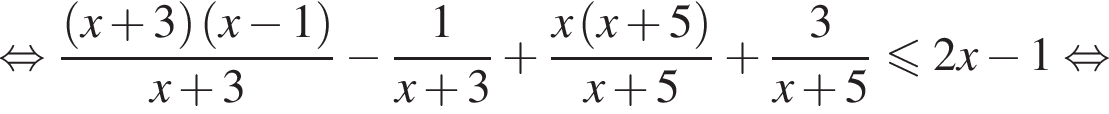



 или
или 










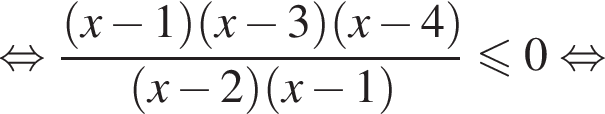









 получаем:
получаем:
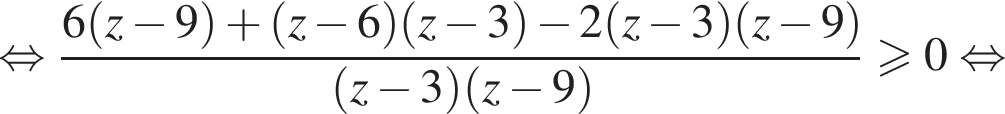
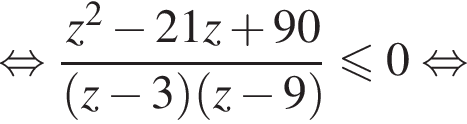



 или
или 

 тогда получим
тогда получим



 получаем:
получаем:
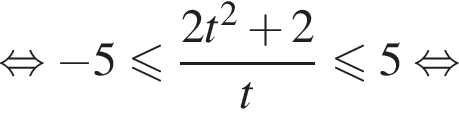
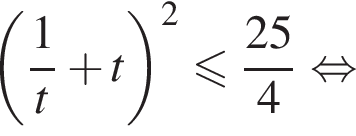


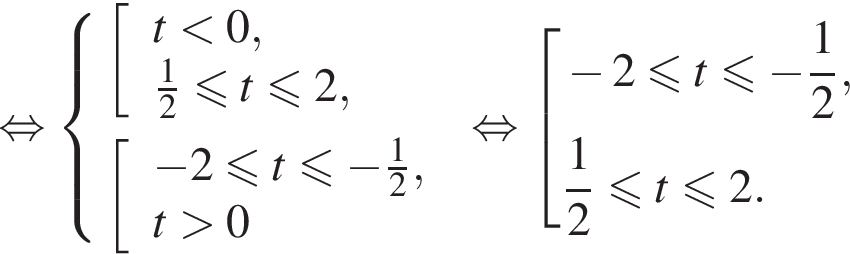
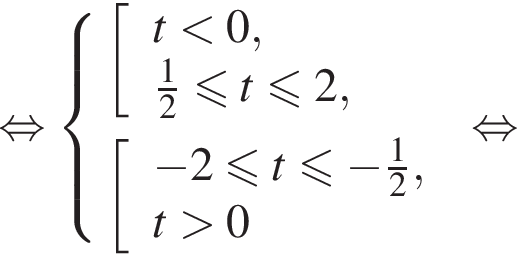

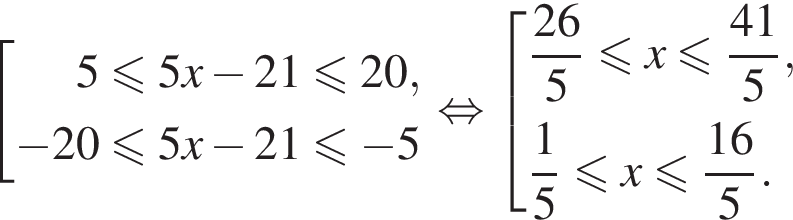


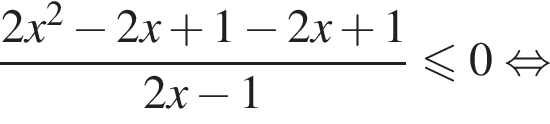





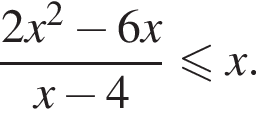
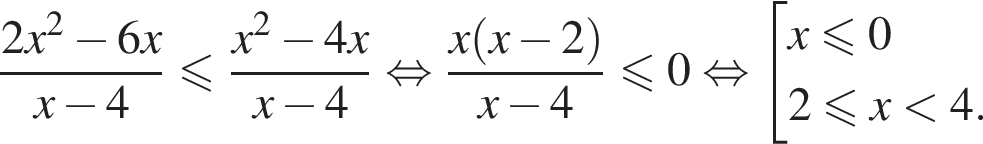












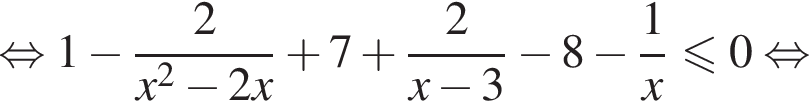





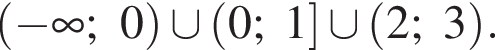











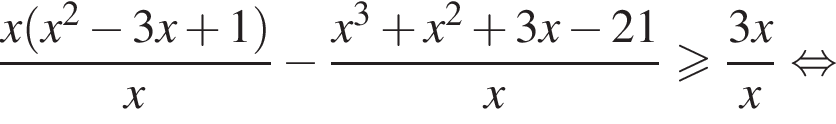
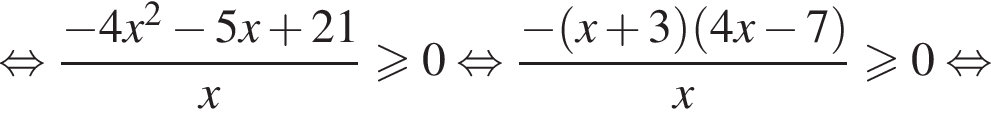





 получаем:
получаем: 







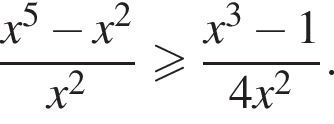







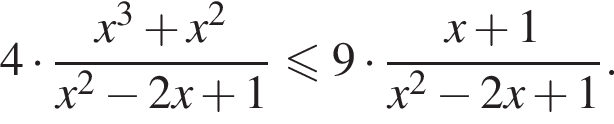







 а их произведение равно
а их произведение равно  Поэтому корни этого уравнения — числа
Поэтому корни этого уравнения — числа 



















 выполнено при всех x, кроме x = –0,7 и x = 0,8.
выполнено при всех x, кроме x = –0,7 и x = 0,8.












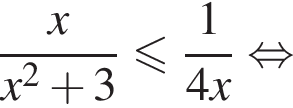




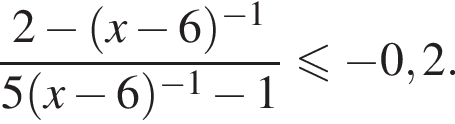
 Получим
Получим


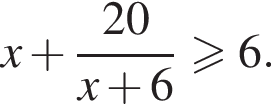




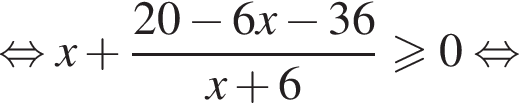
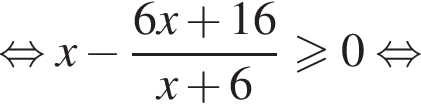





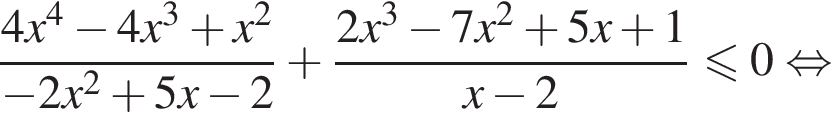











 и
и 

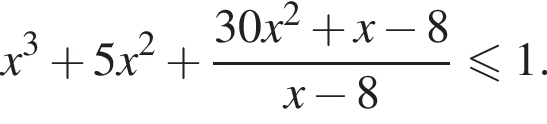


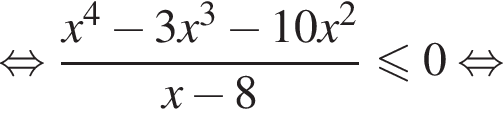

 и
и 
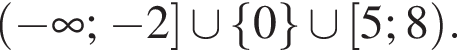

 Получим:
Получим:


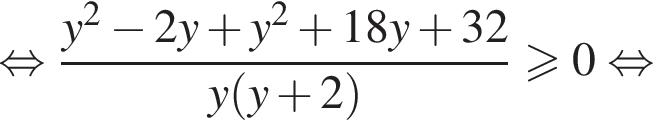










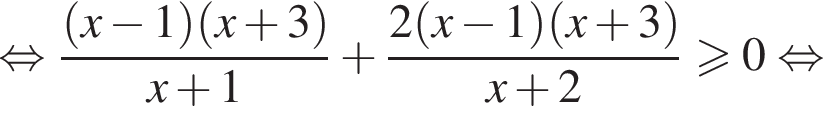




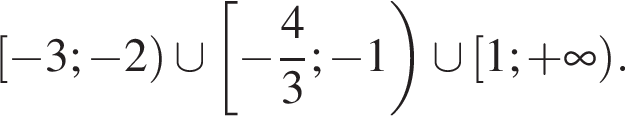

 Применим эту формулу к каждому слагаемому левой части, получим:
Применим эту формулу к каждому слагаемому левой части, получим:


























 по формуле разности кубов, получим:
по формуле разности кубов, получим:



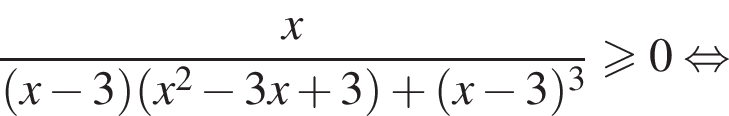
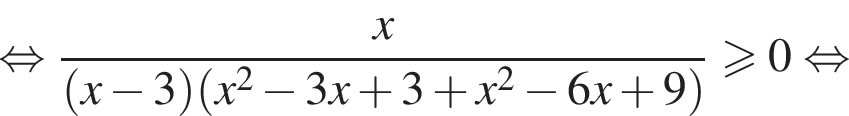












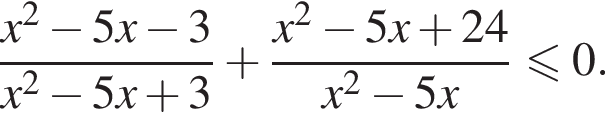
 Получим
Получим



















 :
:



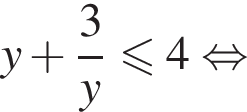
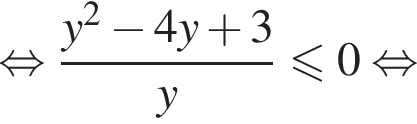




















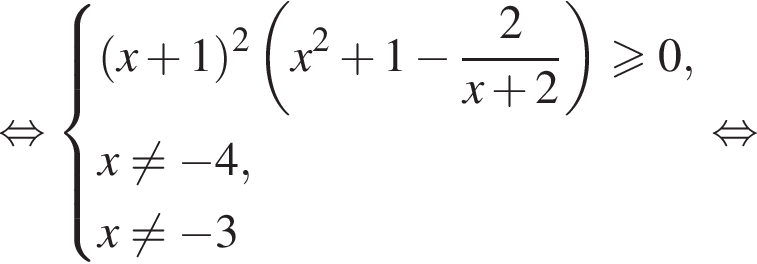









 или
или 









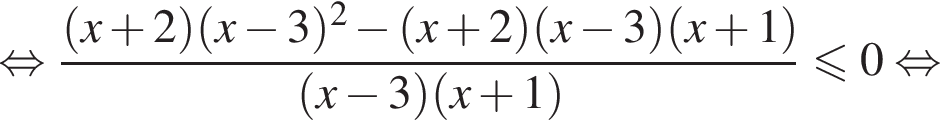





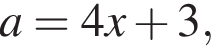
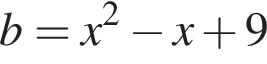 и применим формулу квадрата разности. Получим:
и применим формулу квадрата разности. Получим:







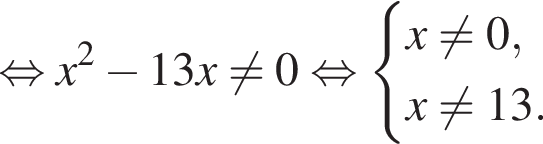













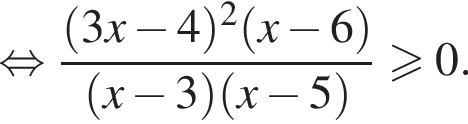
 или
или 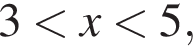 или
или 





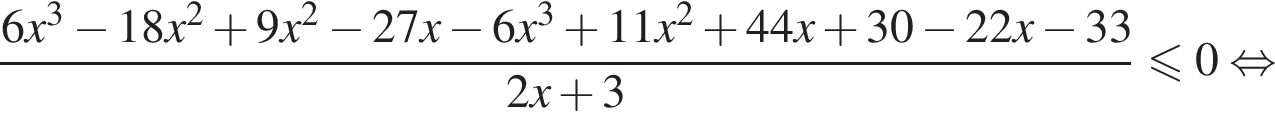



 или
или 













