1. Тип Д11 C3 № 484600 

Классификатор алгебры: Логарифмические неравенства, Неравенства с модулями, Системы неравенств
Методы алгебры: Метод интервалов
Простые системы неравенств. Системы, содержащие логарифмическое неравенство
i
Решите систему неравенств 
Решение. Из первого неравенства имеем 
При этих значениях переменной:
 следовательно,
следовательно, 
Таким образом, имеем:

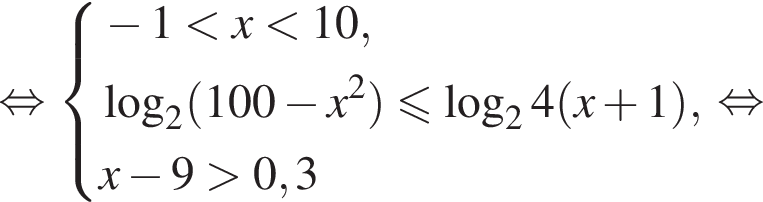
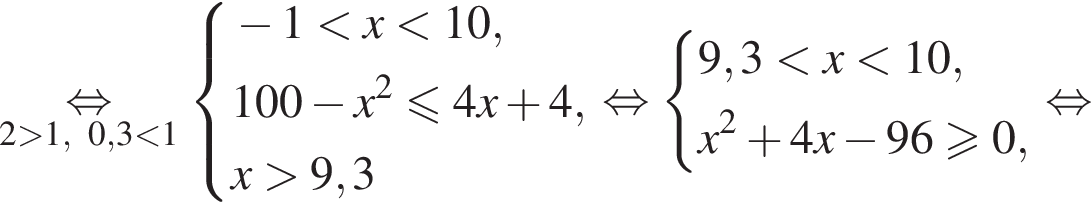








Ответ: 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 3 |
| Обоснованно получены верные ответы в обоих неравенствах системы неравенст | 2 |
| Обоснованно получен верный ответ в одном из неравенств системы неравенств | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ответ: 

484600

Классификатор алгебры: Логарифмические неравенства, Неравенства с модулями, Системы неравенств
Методы алгебры: Метод интервалов

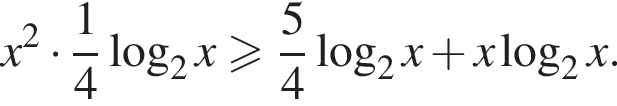




 Получаем:
Получаем: 
 или
или  тогда:
тогда:


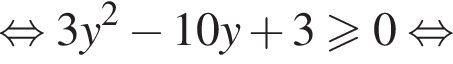














 или
или 
 Пересекая полученные решения, получим множество решений исходного неравенства:
Пересекая полученные решения, получим множество решений исходного неравенства: 




 то
то
 то
то


 или
или 
 Получаем:
Получаем: 


 находим множество решений системы:
находим множество решений системы: 


 имеем:
имеем:








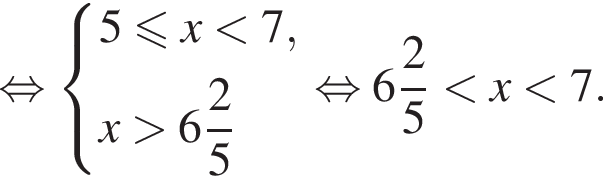

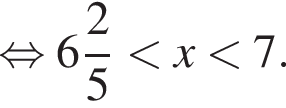

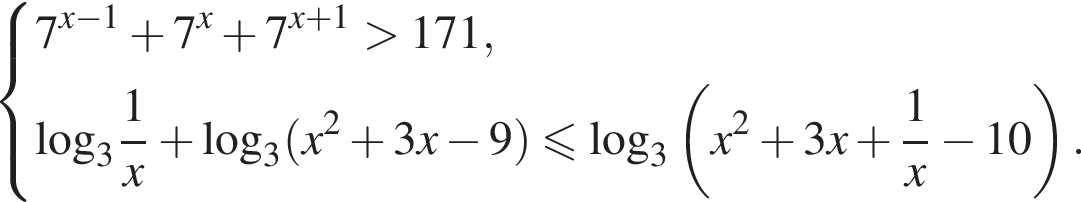
 и
и 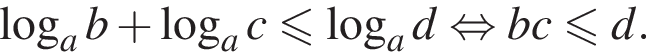

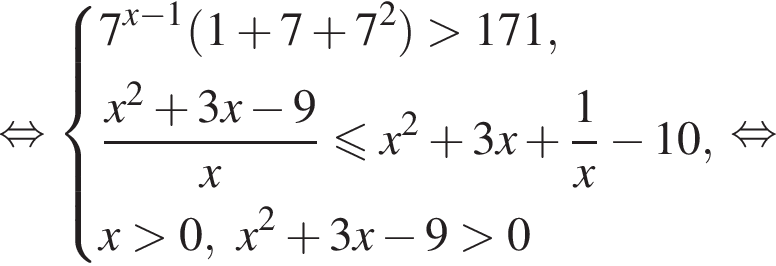








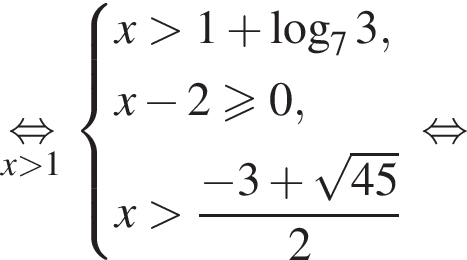














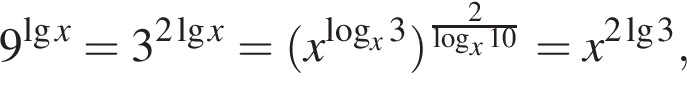 то решая первое неравенство, получаем
то решая первое неравенство, получаем



 получаем:
получаем: 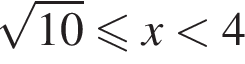


 то решая первое неравенство, получаем
то решая первое неравенство, получаем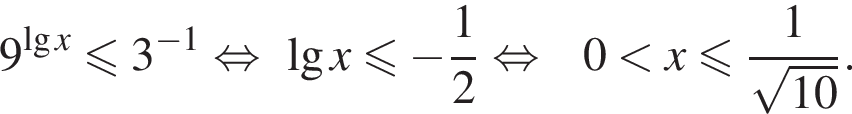





 или
или 
 получаем:
получаем: 


 для первого неравенства имеем:
для первого неравенства имеем:

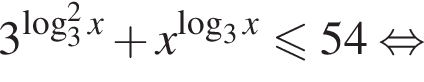









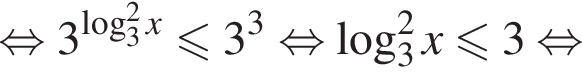


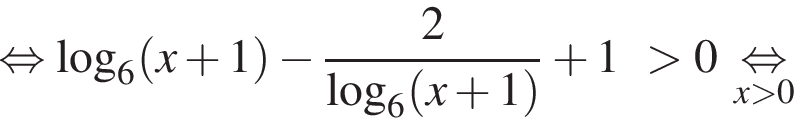
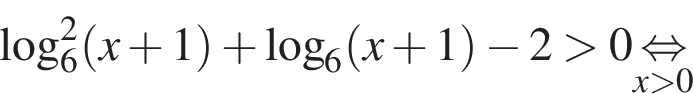

 окончательно получаем
окончательно получаем 


 имеем:
имеем:




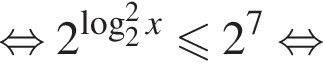
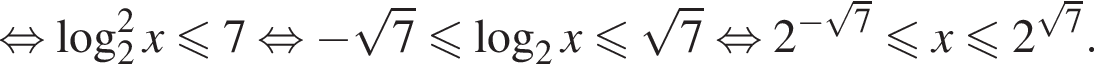
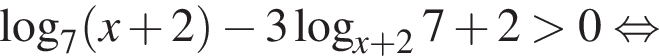

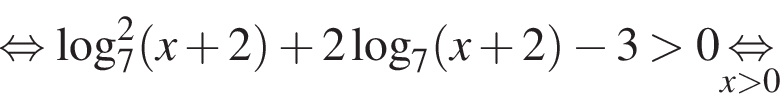

 окончательно получаем
окончательно получаем 


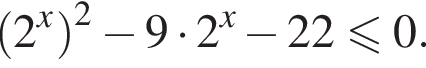





 откуда
откуда 








 и
и 
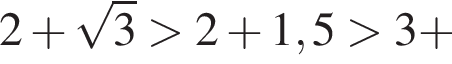



 и поэтому
и поэтому
 Решим неравенство:
Решим неравенство:










 и, значит,
и, значит,  получаем:
получаем:

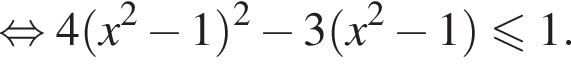
 и получим
и получим  откуда, учитывая, что
откуда, учитывая, что 


 поэтому
поэтому 
 и
и 
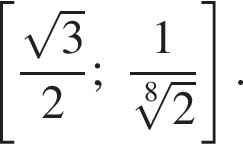

 и поэтому
и поэтому
 Решим неравенство:
Решим неравенство:








 откуда, учитывая, что
откуда, учитывая, что  поэтому
поэтому 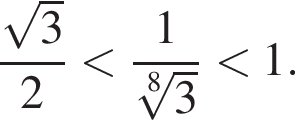
 и
и 

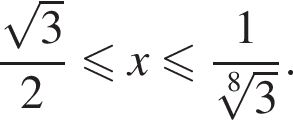



 или
или 

 или
или  Следовательно,
Следовательно,  или
или 








 получаем:
получаем:  откуда находим решение первого неравенства системы
откуда находим решение первого неравенства системы 

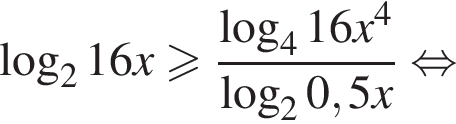

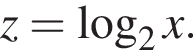









 и
и  получаем множество решений исходной системы неравенств.
получаем множество решений исходной системы неравенств.

 тогда:
тогда:


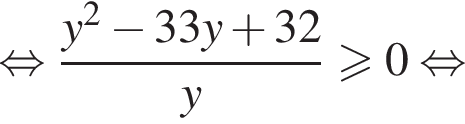

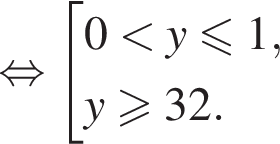

 получаем:
получаем:



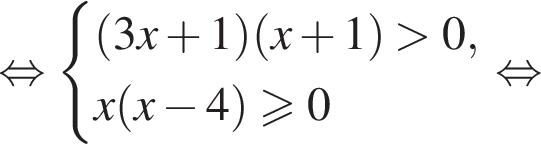











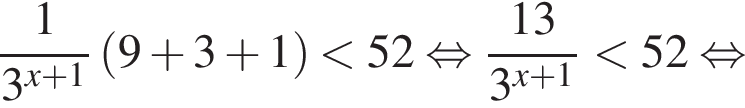






 решение системы неравенств:
решение системы неравенств: 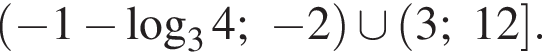


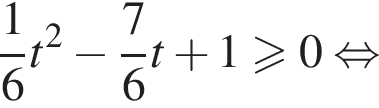



 являются
являются 





