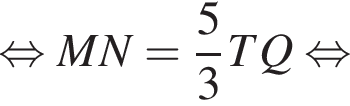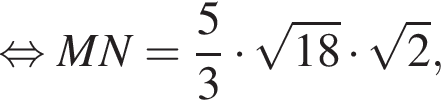В правильную шестиугольную пирамиду, боковое ребро которой равно 10, а высота равна 6, вписана сфера. (Сфера касается всех граней пирамиды.)
а) Докажите, что площадь боковой поверхности пирамиды относится к площади основания как 
б) Найдите площадь этой сферы.
Решение. а) Пусть MH — высота правильной шестиугольной пирамиды
 с вершиной M, тогда треугольник AMH прямоугольный,
с вершиной M, тогда треугольник AMH прямоугольный,  откуда
откуда
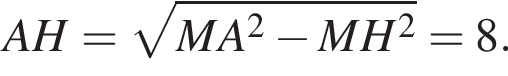
Треугольник ABH равносторонний, следовательно,  В треугольнике AMB высота
В треугольнике AMB высота

В правильном треугольнике AHB высота 
Тогда косинус двугранного угла при основании пирамиды равен  А площадь основания пирамиды есть площадь боковой поверхности пирамиды умножить на косинус двугранного угла при основании. Отсюда и следует требуемое.
А площадь основания пирамиды есть площадь боковой поверхности пирамиды умножить на косинус двугранного угла при основании. Отсюда и следует требуемое.
б) Центр O сферы, вписанной в правильную шестиугольную пирамиду, лежит на её высоте MH, точка K касания сферы и боковой грани AMB лежит на отрезке MN. Треугольники MOK и MNH подобны, поэтому





где r — радиус сферы. Площадь сферы 
Ответ: 
Укажем другой путь нахождения радиуса.
Объем пирамиды равен

Площадь полной поверхности пирамиды равна

Тогда





| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) ИЛИ имеется верное доказательство утверждения пункта а), и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а), ИЛИ при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | 1 |
| Решение не соответствует ни одному из критериев, приведённых выше | 0 |
| Максимальный балл | 3 |


 В треугольнике AMB высота
В треугольнике AMB высота

 поэтому угол, лежащий напротив MH, больше, чем угол, лежащий напротив NH, а значит, больше, чем
поэтому угол, лежащий напротив MH, больше, чем угол, лежащий напротив NH, а значит, больше, чем 





 имеем:
имеем: 







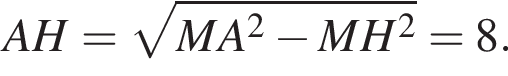
 Рассмотрим сечение пирамиды, проходящее через точки
Рассмотрим сечение пирамиды, проходящее через точки 


 В треугольнике AMB высота
В треугольнике AMB высота 







 где R — радиус меньшего шара. Тогда площадь его поверхности, равная
где R — радиус меньшего шара. Тогда площадь его поверхности, равная  — площадь сечения меньшего шара плоскостью α.
— площадь сечения меньшего шара плоскостью α.  — площадь сечения большего шара плоскостью β.
— площадь сечения большего шара плоскостью β.





 где R — радиус меньшего шара. Тогда площадь его поверхности, равная
где R — радиус меньшего шара. Тогда площадь его поверхности, равная  —
— —
—

 равна
равна 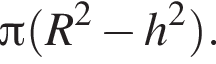 Плоскость α находится от центра шара на расстоянии
Плоскость α находится от центра шара на расстоянии 

 В левой части стоит площадь поверхности малого шара, в правой части — число, не меньшее 24. Утверждение а) доказано.
В левой части стоит площадь поверхности малого шара, в правой части — число, не меньшее 24. Утверждение а) доказано. В левой части стоит площадь сечения большего шара плоскостью α.
В левой части стоит площадь сечения большего шара плоскостью α. Отрезок OH равен
Отрезок OH равен  Высота CH пирамиды CABNM равна
Высота CH пирамиды CABNM равна  Следовательно, объём пирамиды CABNM равен
Следовательно, объём пирамиды CABNM равен



 соответственно.
соответственно.

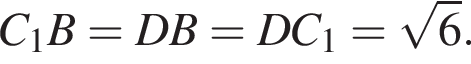 Тогда
Тогда  Значит, все рёбра тетраэдра DBC1P равны, поэтому он правильный.
Значит, все рёбра тетраэдра DBC1P равны, поэтому он правильный. Раcстояние от точки P до точки A равно
Раcстояние от точки P до точки A равно

 и
и  Отсюда вычислим
Отсюда вычислим 

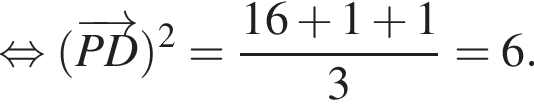


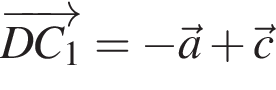 и
и  :
:
 и
и  Все ребра равны, значит, PDBC1 — правильный тетраэдр.
Все ребра равны, значит, PDBC1 — правильный тетраэдр. 





 Следовательно,
Следовательно, 


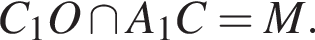 ABCD — квадрат, поэтому имеем:
ABCD — квадрат, поэтому имеем: 
 как накрест лежащие и
как накрест лежащие и  как вертикальные, получаем:
как вертикальные, получаем:  по двум углам, тогда
по двум углам, тогда 
 откуда
откуда 


 поскольку
поскольку 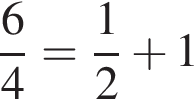 верно. Тогда, по теореме, обратной теореме Пифагора, ΔOMC прямоугольный, ∠M = 90°.
верно. Тогда, по теореме, обратной теореме Пифагора, ΔOMC прямоугольный, ∠M = 90°.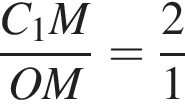 и
и  — правильный, поэтому M — точка пересечения медиан, биссектрис и высот ΔBDC1, то есть центр описанной окружности.
— правильный, поэтому M — точка пересечения медиан, биссектрис и высот ΔBDC1, то есть центр описанной окружности. по теореме косинусов
по теореме косинусов 


 — правильный тетраэдр, что и требовалось доказать.
— правильный тетраэдр, что и требовалось доказать. по теореме косинусов
по теореме косинусов 

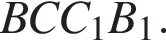
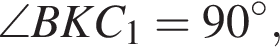 поскольку BC1 — диаметр окружности, поэтому
поскольку BC1 — диаметр окружности, поэтому 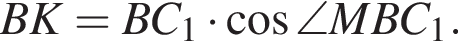
 поэтому
поэтому  откуда
откуда 
 получаем ответ
получаем ответ 
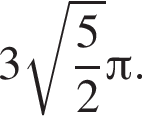
 диагональ трапеции ВН найдем из прямоугольного треугольника ВНD:
диагональ трапеции ВН найдем из прямоугольного треугольника ВНD: 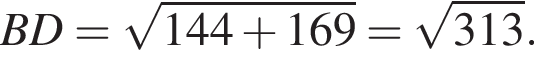
 для радиуса описанной окружности получаем:
для радиуса описанной окружности получаем:





 EB = 2a,
EB = 2a,  Координаты точек будут
Координаты точек будут 

 Тогда
Тогда 




 и, таким образом, угол между прямыми
и, таким образом, угол между прямыми 




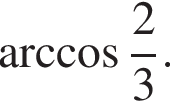







 Далее воспользуемся свойством секущих:
Далее воспользуемся свойством секущих:  откуда
откуда





 где r — радиус сферы, h — высота сферического сегмента. Чтобы найти высоту, проведем перпендикуляр KL из точки K на отрезок AO. Прямоугольные треугольники ABO и AKL подобны по острому углу. Из пункта а) сразу следует, что коэффициент подобия этих треугольников равен 33/65. Тогда:
где r — радиус сферы, h — высота сферического сегмента. Чтобы найти высоту, проведем перпендикуляр KL из точки K на отрезок AO. Прямоугольные треугольники ABO и AKL подобны по острому углу. Из пункта а) сразу следует, что коэффициент подобия этих треугольников равен 33/65. Тогда:



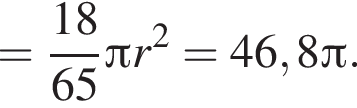

 — прямоугольник. При этом
— прямоугольник. При этом  где R — радиус цилиндра,
где R — радиус цилиндра,  Таким образом, в прямоугольном треугольнике BCB' угол CBB' равен 30°, и, следовательно, угол BCB' равен 60°.
Таким образом, в прямоугольном треугольнике BCB' угол CBB' равен 30°, и, следовательно, угол BCB' равен 60°.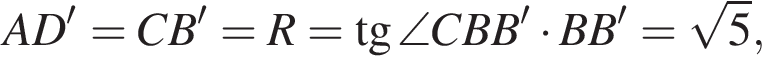



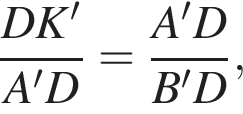 откуда
откуда 
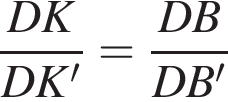 откуда
откуда







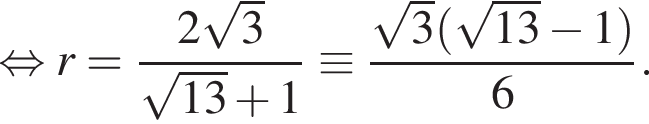

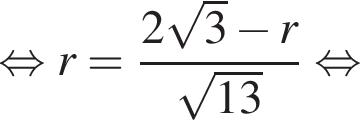



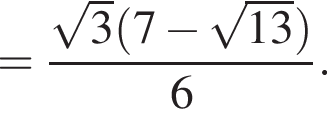






 Следовательно, расстояние от центра шара до плоскости α больше радиуса, и шар с плоскостью не пересекается.
Следовательно, расстояние от центра шара до плоскости α больше радиуса, и шар с плоскостью не пересекается.
 где V — объем пирамиды, Sп.п. — площадь полной поверхности пирамиды. Площадь основания пирамиды равна
где V — объем пирамиды, Sп.п. — площадь полной поверхности пирамиды. Площадь основания пирамиды равна 


 высота пирамиды равна
высота пирамиды равна


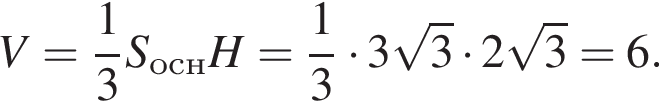
 где p — полупериметр основания,
где p — полупериметр основания,  —
—




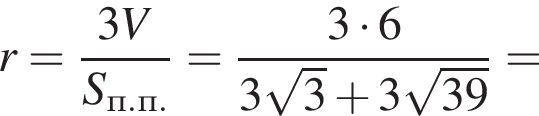

 поэтому плоскость α и шар не имеют общих точек.
поэтому плоскость α и шар не имеют общих точек. Тангенс угла между прямой BC и плоскостью ABF равен 2, а точка M выбрана на ребре BC так, что
Тангенс угла между прямой BC и плоскостью ABF равен 2, а точка M выбрана на ребре BC так, что  Точка T лежит на прямой AF и равноудалена от точек
Точка T лежит на прямой AF и равноудалена от точек 
 то есть AC = 2BC. Находим:
то есть AC = 2BC. Находим: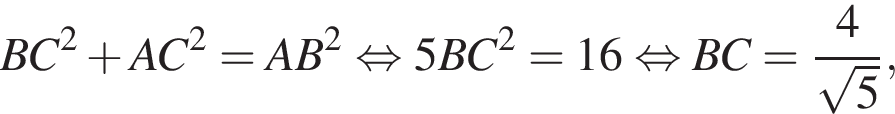

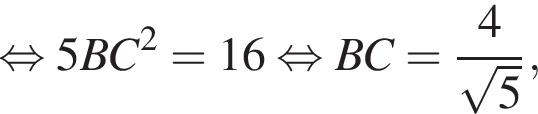

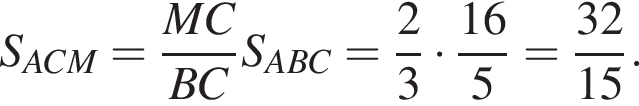






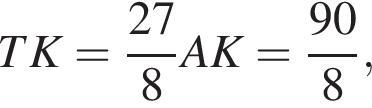


 Из подобия прямоугольных треугольников KEH и HED получаем
Из подобия прямоугольных треугольников KEH и HED получаем 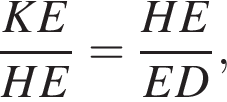 откуда находим:
откуда находим:


 откуда
откуда  Из п. а) боковые ребра пирамиды равны 3a, ребра основания —
Из п. а) боковые ребра пирамиды равны 3a, ребра основания — 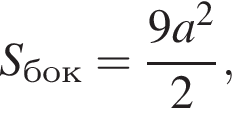 площадь основания
площадь основания  следовательно,
следовательно, 




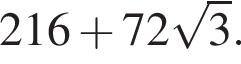


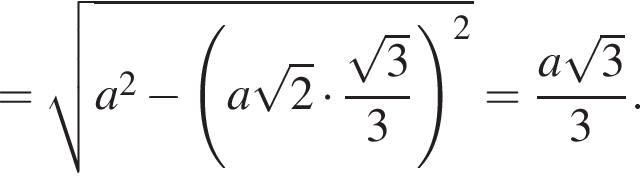

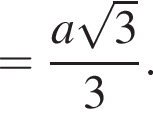


 значит,
значит,  Из подобия треугольников PTQ и PMN по двум углам получаем:
Из подобия треугольников PTQ и PMN по двум углам получаем: