Ре­ше­ние. а)  Пусть O  — центр окруж­но­сти, впи­сан­ной в пря­мо­уголь­ную тра­пе­цию ABCD с ос­но­ва­ни­я­ми AD и BC, O₁  — центр окруж­но­сти, ка­са­ю­щей­ся боль­шей бо­ко­вой сто­ро­ны и про­дол­же­ний ос­но­ва­ний тра­пе­ции (рис. 1).

Точка O лежит на бис­сек­три­сах углов BCD и ADC, сле­до­ва­тель­но,

Точка O₁ лежит на бис­сек­три­се угла, смеж­но­го с углом BCD, зна­чит, Ана­ло­гич­но, углы CO₁D и ODO₁  — пря­мые. Зна­чит, OCO₁D  — пря­мо­уголь­ник, по­это­му CD  =  OO₁.

б)  Пусть окруж­ность, впи­сан­ная в тра­пе­цию ABCD, ка­са­ет­ся сто­ро­ны AD в точке P, а сто­ро­ны CD  — в точке M, вто­рая окруж­ность ка­са­ет­ся пря­мой AD в точке Q (рис. 2).

Ра­ди­у­сы окруж­но­стей OP и O₁Q равны по­ло­ви­не рас­сто­я­ния между па­рал­лель­ны­ми пря­мы­ми AD и BC. По­лу­ча­ем, что OO₁QP  — пря­мо­уголь­ник, сле­до­ва­тель­но, OO₁  =  PQ.

В пря­мо­уголь­ном тре­уголь­ни­ке COD имеем:

В пря­мо­уголь­ном тре­уголь­ни­ке AQO₁ имеем:

Рас­сто­я­ние от вер­ши­ны пря­мо­го угла тра­пе­ции до цен­тра вто­рой окруж­но­сти равно

Ответ:

Ре­ше­ние. а)  Пусть O₁  — центр окруж­но­сти, ко­то­рая ка­са­ет­ся от­рез­ка CD, O₂  — центр окруж­но­сти, ко­то­рая ка­са­ет­ся от­рез­ка CE, R  — ра­ди­ус окруж­но­стей. Окруж­ность с цен­тром O₁ ка­са­ет­ся от­рез­ка CD в точке K, а пря­мой DE  — в точке M; окруж­ность с цен­тром O₂ ка­са­ет­ся от­рез­ка CE в точке L, а пря­мой DE  — в точке N (рис. 1).

По­лу­ча­ем, что AO₁O₂B и MO₁O₂N  — пря­мо­уголь­ни­ки, сле­до­ва­тель­но, AB  =  O₁O₂ и MN  =  O₁O₂.

По свой­ству ка­са­тель­ных CA  =  CK, DM  =  DK, CB  =  CL, EL  =  EN.

Тогда пе­ри­метр тре­уголь­ни­ка CDE

б)  Точка O₁ лежит на бис­сек­три­сах углов MDC и ACD (рис. 2), сле­до­ва­тель­но,

В пря­мо­уголь­ном тре­уголь­ни­ке CO₁D имеем:

Ана­ло­гич­но По­лу­ча­ем, что

Ответ: 12,375.

Ре­ше­ние. Пря­мые AD и BC па­рал­лель­ны, по­это­му ∠ACB = ∠CAD.

Пред­по­ло­жим, что ∠BAC = ∠ACD, тогда по­лу­ча­ем, что пря­мые AB и CD па­рал­лель­ны и ABCD  — па­рал­ле­ло­грамм. Зна­чит, пред­по­ло­же­ние не­вер­но и ∠ABC = ∠ACD.

б)  Тре­уголь­ни­ки ABC и DCA по­доб­ны. Сле­до­ва­тель­но, от­ку­да

Опу­стим из вер­ши­ны C пер­пен­ди­ку­ляр CK на ос­но­ва­ние AD. Тогда Зна­чит, ABCK  — пря­мо­уголь­ник.

Сле­до­ва­тель­но,

Пусть N и M  — се­ре­ди­ны ос­но­ва­ний AD и BC со­от­вет­ствен­но, MH  — пер­пен­ди­ку­ляр к AD. Тогда ABMH  — пря­мо­уголь­ник. По­лу­ча­ем, что

В пря­мо­уголь­ном тре­уголь­ни­ке MNH имеем:

Ответ:

При­ве­дем ре­ше­ние John Titor.

Тре­уголь­ни­ки ABC и DCA по­доб­ны. Сле­до­ва­тель­но, от­ку­да

Пусть N и M  — се­ре­ди­ны ос­но­ва­ний AD и BC со­от­вет­ствен­но. Про­ве­дем через точку C пря­мую, па­рал­лель­ную пря­мой MN. Пусть E  — точка пе­ре­се­че­ния этой пря­мой и от­рез­ка AD. NMCE  — па­рал­ле­ло­грамм, сле­до­ва­тель­но,

В тре­уголь­ни­ке ACE по тео­ре­ме ко­си­ну­сов най­дем CE:

Сле­до­ва­тель­но,

Ре­ше­ние. а)  Пусть тогда и Тре­уголь­ник BOC рав­но­бед­рен­ный. Сле­до­ва­тель­но,

Сле­до­ва­тель­но, точки O, B, K и C лежат на одной окруж­но­сти. Сле­до­ва­тель­но, четырёхуголь­ник OBKC впи­сан­ный.

б)  По усло­вию по­это­му

Из тео­ре­мы си­ну­сов по­лу­ча­ем со­от­но­ше­ние для ра­ди­у­са окруж­но­сти, опи­сан­ной около тре­уголь­ни­ка ABC. Таким об­ра­зом,

Пусть R  — ра­ди­ус окруж­но­сти, опи­сан­ной около четырёхуголь­ни­ка OBKC. В тре­уголь­ни­ке OCK имеем:

Ответ: 25.

Ре­ше­ние. а)  Пусть тогда как углы при ос­но­ва­нии рав­но­бед­рен­но­го тре­уголь­ни­ка OBC. Из усло­вия сле­ду­ет, что Тогда От­ку­да, по свой­ству впи­сан­ных углов, сле­ду­ет, что точки О, В, К, С лежат на одной окруж­но­сти.

б)  По усло­вию, тогда Рас­смот­рим в нем В обо­зна­че­ни­ях пунк­та а): тогда так как че­ты­рех­уголь­ник OBKC впи­сан­ный.

тогда

Рас­смот­рим тре­уголь­ник KBC:

Ответ:10.

Ре­ше­ние. а)  Пусть P  — ос­но­ва­ние пер­пен­ди­ку­ля­ра, опу­щен­но­го из точки D на пря­мую AB, тогда DH  =  DP. В рав­но­бед­рен­ном тре­уголь­ни­ке EAD угол AED  равен 30°. В пря­мо­уголь­ном тре­уголь­ни­ке EPD на­хо­дим от­ку­да по­лу­ча­ем, что FH  =  2DH.

б)  Пусть AM  — вы­со­та тре­уголь­ни­ка ABC  — пе­ре­се­ка­ет ED в точке N. Тогда

Пусть DH  =  EF  =  x, тогда FH  =  ED  =  2x. Тре­уголь­ни­ки ABC и AED по­доб­ны, сле­до­ва­тель­но,

Зна­чит, пло­щадь пря­мо­уголь­ни­ка DEFH равна

Ответ:

При­ве­дем ре­ше­ние пунк­та а) Сер­гея Фе­до­ро­ва.

Тре­уголь­ник ABC рав­но­бед­рен­ный, сле­до­ва­тель­но,

Углы BDE и DBC равны как на­крест ле­жа­щие, угол DBC равен углу DBE, по­сколь­ку BD яв­ля­ет­ся бис­сек­три­сой, сле­до­ва­тель­но, углы BDE и DBE равны, тогда тре­уголь­ник DBE рав­но­бед­рен­ный, DE  =  BE. В тре­уголь­ни­ке BFE катет EF лежит про­тив угла в 30°, сле­до­ва­тель­но, BE  =  2EF, тогда DE  =  2EF.

Ре­ше­ние. а)  Пусть Р  — ос­но­ва­ние пер­пен­ди­ку­ля­ра, опу­щен­но­го из точки D на пря­мую AB, тогда DH  =  DP.

В рав­но­бед­рен­ном тре­уголь­ни­ке EAD угол AED равен 30°.

В пря­мо­уголь­ном тре­уголь­ни­ке

от­ку­да по­лу­ча­ем, что FH  =  2DH.

б)  Пусть AM  — вы­со­та тре­уголь­ни­ка ABC  — пе­ре­се­ка­ет ED в точке N. Тогда

Пусть DH  =  EF  =  x, тогда FH  =  ED  =  2x. Тре­уголь­ни­ки ABC и AED по­доб­ны, сле­до­ва­тель­но

Зна­чит, пло­щадь пря­мо­уголь­ни­ка DEFH равна

Ответ:

----------

Дуб­ли­ру­ет за­да­ние 505249.

Ре­ше­ние.

а)  По­сколь­ку AA₁  — пер­пен­ди­ку­ляр к ВС, а BB₁  — пер­пен­ди­ку­ляр к AС (см. рис.), углы AHB₁ и ACB равны как углы со вза­им­но пер­пен­ди­ку­ляр­ны­ми сто­ро­на­ми.

б)  Сто­ро­на тре­уголь­ни­ка, ве­ли­чи­на про­ти­во­ле­жа­ще­го ей угла и от­ре­зок вы­со­ты, про­ведённой из вер­ши­ны этого угла в точку пе­ре­се­че­ния высот тре­уголь­ни­ка, свя­за­ны со­от­но­ше­ни­ем:

Ответ:

При­ведём ав­тор­ское ре­ше­ние.

а)  В четырёхуголь­ни­ке углы и   — пря­мые, сле­до­ва­тель­но, около этого четырёхуголь­ни­ка можно опи­сать окруж­ность, причём AH  — её диа­метр. Впи­сан­ные углы и опи­ра­ют­ся на одну дугу, сле­до­ва­тель­но,

Углы и   — пря­мые, зна­чит, точки и лежат на окруж­но­сти с диа­мет­ром Сле­до­ва­тель­но,

По­лу­ча­ем, что

б)  В тре­уголь­ни­ке диа­метр опи­сан­ной окруж­но­сти от­ку­да

В пря­мо­уголь­ном тре­уголь­ни­ке имеем:

В пря­мо­уголь­ном тре­уголь­ни­ке имеем:

По­лу­ча­ем, что Тре­уголь­ни­ки ABC и имеют общий угол A и сле­до­ва­тель­но, они по­доб­ны. Тогда Зна­чит,

При­ведём ре­ше­ние Егора Ва­ля­е­ва из Аль­ме­тьев­ска.

а)  Рас­смот­рим тре­уголь­ник B₁AH. Пусть угол AHB₁ равен α, тогда ∠HAB₁  =  90° − α. Опу­стим из точки A вы­со­ту AA₁ на сто­ро­ну BC. Рас­смот­рим тре­уголь­ник AA₁C, в ко­то­ром ∠A₁CA  =  180° − ∠AA₁C − ∠A₁AC (углы HAB₁ и A₁AC равны и ∠A₁AC  =  90° − α). Вы­чис­лим угол A₁CA  =  180° − 90° − (90° − α)  =  α, сле­до­ва­тель­но, ∠ACB = ∠A₁CA  =  α = ∠AHB₁.

б)  Рас­смот­рим тре­уголь­ник B₁AB, в нем ∠BAB₁  =  30°, от­ку­да по­лу­ча­ем:

а зна­чит, и от­ку­да

Рас­смот­рим те­перь тре­уголь­ник AHB₁ и за­ме­тим, что

На­ко­нец, рас­смот­рим тре­уголь­ник B₁BC: в нем Так как из пунк­та а) из­вест­но, что углы BCB₁, ACB и AHB₁ равны, имеем:

Тогда

Ре­ше­ние. а)  Пусть угол BAC  =  α. Углы BAC и KHB равны как углы с вза­им­но пер­пен­ди­ку­ляр­ны­ми сто­ро­на­ми. Рас­смот­рим четырёхуголь­ник BKHM: в нем ∠BKH + ∠BMH  =  90° + 90°  =  180°, сле­до­ва­тель­но, четырёхуголь­ник BKHM впи­сан в окруж­ность. Зна­чит, углы KHB и KMB  — впи­сан­ные, опи­ра­ю­щи­е­ся на одну и ту же дугу, сле­до­ва­тель­но, они равны. Таким об­ра­зом, ∠BAC = ∠KHB = ∠KMB. Тре­уголь­ни­ки ABC и MBK имеют общий угол B, а ∠BAC = ∠KMB, зна­чит, эти тре­уголь­ни­ки по­доб­ны по двум углам.

б)  Сумма углов К и М че­ты­рех­уголь­ни­ка BKHM равна 180°, по­это­му он впи­сан в окруж­ность. Пря­мо­уголь­ный тре­уголь­ник BKH впи­сан в эту же окруж­ность, а по­то­му ра­ди­ус R окруж­но­сти равен по­ло­ви­не ги­по­те­ну­зы BH: R  =  1. Тре­уголь­ник MBK также впи­сан в эту окруж­ность. Ко­эф­фи­ци­ент по­до­бия тре­уголь­ни­ков ABC и MBK равен от­но­ше­нию их сход­ствен­ных эле­мен­тов, по­это­му он равен Тогда для от­но­ше­ния пло­ща­ди тре­уголь­ни­ка MBK к пло­ща­ди четырёхуголь­ни­ка AKMC по­лу­ча­ем:

Ответ:

При­ве­дем дру­гое ре­ше­ние пунк­та б).

Из пря­мо­уголь­но­го тре­уголь­ни­ка BKH на­хо­дим, что Для тре­уголь­ни­ка ABC спра­вед­ли­во ра­вен­ство Учи­ты­вая, что ∠KHB = ∠BAC, по­лу­ча­ем: Сто­ро­ны BC и BK  — сход­ствен­ные в по­доб­ных тре­уголь­ни­ках ABC и MBK, сле­до­ва­тель­но, их ко­эф­фи­ци­ент по­до­бия Найдём от­но­ше­ние пло­ща­ди тре­уголь­ни­ка MBK к пло­ща­ди четырёхуголь­ни­ка AKMC:

Ре­ше­ние. а)  Пусть угол Углы BAC и KHB равны, как углы с вза­им­но пер­пен­ди­ку­ляр­ны­ми сто­ро­на­ми. Рас­смот­рим четырёхуголь­ник BKHM сле­до­ва­тель­но, четырёхуголь­ник BKHM впи­сан в окруж­ность. Зна­чит, углы KHB и KMB  — впи­сан­ные, опи­ра­ю­щи­е­ся на одну и ту же дугу, сле­до­ва­тель­но, они равны. Таким об­ра­зом, Тре­уголь­ни­ки ABC и MBK имеют общий угол B и зна­чит, эти тре­уголь­ни­ки по­доб­ны по двум углам.

б)  Из пря­мо­уголь­но­го тре­уголь­ни­ка BKH на­хо­дим, что Для тре­уголь­ни­ка ABC спра­вед­ли­во ра­вен­ство Учи­ты­вая, что по­лу­ча­ем: Сто­ро­ны BC и BK  — сход­ствен­ные в по­доб­ных тре­уголь­ни­ках ABC и MBK, сле­до­ва­тель­но, их ко­эф­фи­ци­ент по­до­бия Найдём от­но­ше­ние пло­ща­ди тре­уголь­ни­ка MBK к пло­ща­ди четырёхуголь­ни­ка

Ответ:

----------

Дуб­ли­ру­ет за­да­ние 505495.

Ре­ше­ние. а)  В четырёхуголь­ни­ке углы и   — пря­мые, сле­до­ва­тель­но, около этого четырёхуголь­ни­ка можно опи­сать окруж­ность, причём AH  — её диа­метр. Впи­сан­ные углы и опи­ра­ют­ся на одну дугу, сле­до­ва­тель­но,

Углы и   — пря­мые, зна­чит, точки и лежат на окруж­но­сти с диа­мет­ром Сле­до­ва­тель­но,

По­лу­ча­ем, что

б)  В тре­уголь­ни­ке диа­метр опи­сан­ной окруж­но­сти от­ку­да

В пря­мо­уголь­ном тре­уголь­ни­ке имеем:

В пря­мо­уголь­ном тре­уголь­ни­ке имеем:

По­лу­ча­ем, что Тре­уголь­ни­ки ABC и имеют общий угол A и сле­до­ва­тель­но, они по­доб­ны. Тогда Зна­чит,

Ответ: 24.

----------

Дуб­ли­ру­ет за­да­ние 505419.

Ре­ше­ние. а)  В четырёхуголь­ни­ке углы и   — пря­мые, сле­до­ва­тель­но, около этого четырёхуголь­ни­ка можно опи­сать окруж­ность, причём AH  — её диа­метр. Впи­сан­ные углы и опи­ра­ют­ся на одну дугу, сле­до­ва­тель­но,

Углы и   — пря­мые, зна­чит, точки и лежат на окруж­но­сти с диа­мет­ром Сле­до­ва­тель­но,

По­лу­ча­ем, что

б)  В тре­уголь­ни­ке диа­метр опи­сан­ной окруж­но­сти от­ку­да

В пря­мо­уголь­ном тре­уголь­ни­ке имеем:

В пря­мо­уголь­ном тре­уголь­ни­ке имеем:

По­лу­ча­ем, что Тре­уголь­ни­ки ABC и имеют общий угол A и сле­до­ва­тель­но, они по­доб­ны. Тогда Зна­чит,

Ответ:

При­ведём дру­гое ре­ше­ние.

а)  По­сколь­ку AA₁  — пер­пен­ди­ку­ляр к ВС, а BB₁  — пер­пен­ди­ку­ляр к AС (см. рис.), углы AHB₁ и ACB равны как углы со вза­им­но пер­пен­ди­ку­ляр­ны­ми сто­ро­на­ми.

б)  Сто­ро­на тре­уголь­ни­ка, ве­ли­чи­на про­ти­во­ле­жа­ще­го ей угла и от­ре­зок вы­со­ты, про­ведённой из вер­ши­ны этого угла в точку пе­ре­се­че­ния высот тре­уголь­ни­ка, свя­за­ны со­от­но­ше­ни­ем: от­ку­да

----------

Дуб­ли­ру­ет за­да­ние 505425.

Ре­ше­ние. а)  Угол KBC равен углу BAC как угол между ка­са­тель­ной и хор­дой. Пря­мые AB и CK па­рал­лель­ны. Сле­до­ва­тель­но, По­лу­ча­ем, что тре­уголь­ни­ки ABC и BCK по­доб­ны. Сле­до­ва­тель­но,

Зна­чит, тре­уголь­ник BCK  — рав­но­бед­рен­ный.

б)  Тре­уголь­ни­ки ABC и BCK по­доб­ны, ко­эф­фи­ци­ент по­до­бия равен От­но­ше­ние пло­ща­дей В тре­уголь­ни­ке ABC имеем:

Ответ: 2.

----------

Дуб­ли­ру­ет за­да­ние 505431.

Ре­ше­ние. а)  Обо­зна­чим K точку пе­ре­се­че­ния от­рез­ков AM и BN. Тре­уголь­ник ABN рав­но­бед­рен­ный, так как в нем AK яв­ля­ет­ся бис­сек­три­сой и вы­со­той. Сле­до­ва­тель­но, AK яв­ля­ет­ся и ме­ди­а­ной, то есть K  — се­ре­ди­на BN. По­лу­ча­ем, что AN = AB = 6, от­ку­да NC  =  AC − AN  =  3.

Рас­смот­рим тре­уголь­ник ABC, бис­сек­три­са делит про­ти­во­по­лож­ную сто­ро­ну на от­рез­ки, про­пор­ци­о­наль­ные при­ле­жа­щим сто­ро­нам: BM : MC = AB : AC, учи­ты­вая, что длина BC равна 5, по­лу­ча­ем: BM = 2; MC = 3.

В тре­уголь­ни­ке MNC сто­ро­ны NC и MC равны, сле­до­ва­тель­но, тре­уголь­ник MNC  — рав­но­бед­рен­ный, с ос­но­ва­ни­ем MN. Зна­чит, бис­сек­три­са угла C также яв­ля­ет­ся ме­ди­а­ной и вы­со­той. Таким об­ра­зом, по­лу­ча­ем, что бис­сек­три­са угла С делит от­ре­зок MN по­по­лам.

б)  Рас­смот­рим тре­уголь­ник PMN: от­ре­зок PO пер­пен­ди­ку­ля­рен пря­мой MN и делит её по­по­лам, сле­до­ва­тель­но, тре­уголь­ник PMN  — рав­но­бед­рен­ный с ос­но­ва­ни­ем MN. Зна­чит, PM = PN и от­но­ше­ние AP : PN = AP : PM.

В тре­уголь­ни­ке AMC от­ре­зок CP  — бис­сек­три­са, по­это­му AP : PM = AC : MC = 3 : 1.

Ответ: 3 : 1.

При­ве­дем дру­гое ре­ше­ние.

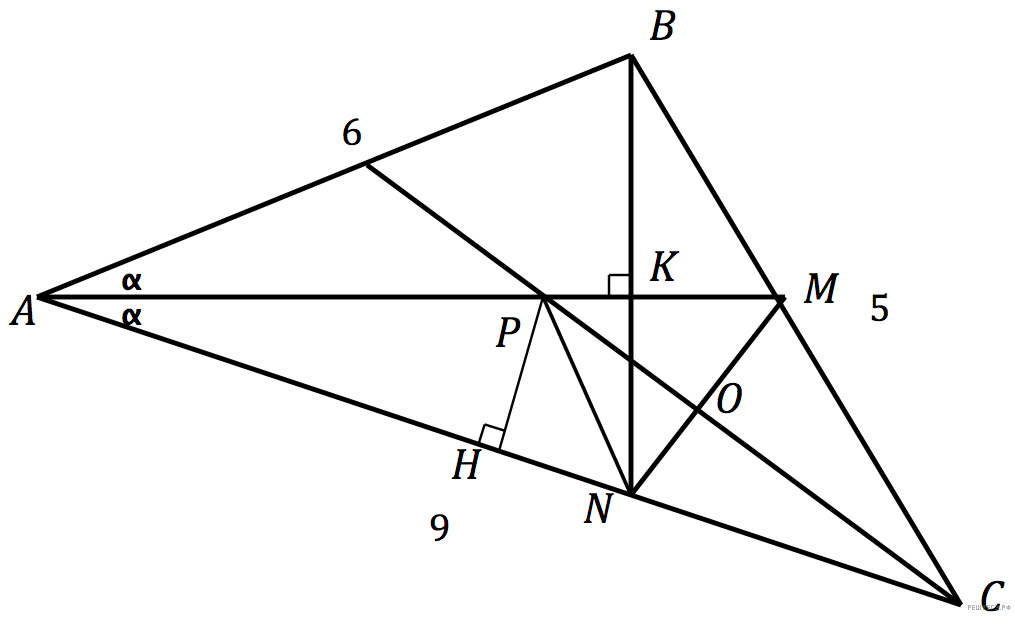а)  Обо­зна­чим за K точку пе­ре­се­че­ния от­рез­ков AM и BN. Тре­уголь­ник ABN рав­но­бед­рен­ный, так как в нем AK яв­ля­ет­ся бис­сек­три­сой и вы­со­той. Сле­до­ва­тель­но, AK яв­ля­ет­ся и ме­ди­а­ной, то есть K  — се­ре­ди­на BN. По­лу­ча­ем, что AN = AB = 6, от­ку­да NC  =  AC − AN  =  3.

Далее, в видим, что KM яв­ля­ет­ся вы­со­той и ме­ди­а­ной, от­ку­да сле­ду­ет, что тре­уголь­ник BMN рав­но­бед­рен­ный. Обо­зна­чим BM = MN = x, тогда MC = BC − BM = 5 − x.

Из по тео­ре­ме ко­си­ну­сов по­лу­ча­ем:

Из тре­уголь­ни­ка по тео­ре­ме ко­си­ну­сов: от­ку­да:

Таким об­ра­зом, по­лу­чи­ли, что MN = 2, MC = 3  — зна­чит, тре­уголь­ник MCN рав­но­бед­рен­ный, от­ку­да сле­ду­ет, что бис­сек­три­са CO яв­ля­ет­ся и вы­со­той, и ме­ди­а­ной. Зна­чит, точка O  — се­ре­ди­на сто­ро­ны MN. Что и тре­бо­ва­лось до­ка­зать.

б)  Опу­стим вспо­мо­га­тель­ный пер­пен­ди­ку­ляр из точки P на сто­ро­ну AN (пе­ре­се­че­ние в точке H). От­ре­зок PH яв­ля­ет­ся ра­ди­у­сом впи­сан­ной окруж­но­сти, так как P  — точка пе­ре­се­че­ния бис­сек­трис (а зна­чит  — центр впи­сан­ной окруж­но­сти). Най­дем ра­ди­ус из фор­му­лы где S  — пло­щадь тре­уголь­ни­ка ABC, p  — по­лу­пе­ри­метр тре­уголь­ни­ка, рав­ный

Най­дем пло­щадь по фор­му­ле Ге­ро­на:

Тогда

Из тре­уголь­ни­ка ABC вновь по тео­ре­ме ко­си­ну­сов най­дем ко­си­нус угла A (обо­зна­чим его за ):

Так как то

Тогда из по­лу­ча­ем:

Най­дем, что HN = AN − AH = 1, тогда из по тео­ре­ме Пи­фа­го­ра:

Окон­ча­тель­но по­лу­ча­ем, что

Ответ: 3 : 1.

----------

Дуб­ли­ру­ет за­да­ние 505501.