1. Тип 15 № 507779 

Классификатор алгебры: Иррациональные неравенства, Неравенства смешанного типа, Неравенства, рациональные относительно логарифмической функции
Методы алгебры: Введение замены
Кодификатор ФИПИ/Решу ЕГЭ: 2.2.9 Метод интервалов
Неравенства. Логарифмы и иррациональности
i
Решите неравенство: 
Решение. После замены  получаем
получаем  Значит,
Значит,
 или
или 
Решим первую систему неравенств:





Возвращаясь к исходной переменной, получаем:

Решим вторую систему неравенств:



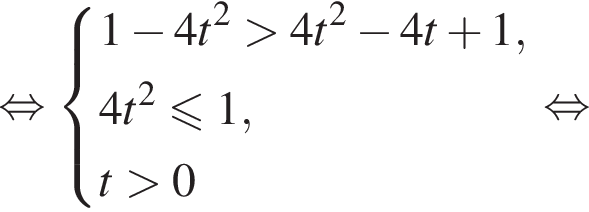
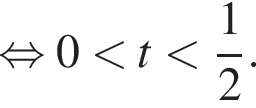
Возвращаясь к исходной переменной, получаем:

Таким образом, решением исходного неравенства является множество 
Ответ: 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 2 |
| Обоснованно получен ответ, отличающийся от верного исключением точек, ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Ответ: 

507779

Классификатор алгебры: Иррациональные неравенства, Неравенства смешанного типа, Неравенства, рациональные относительно логарифмической функции
Методы алгебры: Введение замены
Кодификатор ФИПИ/Решу ЕГЭ: 2.2.9 Метод интервалов


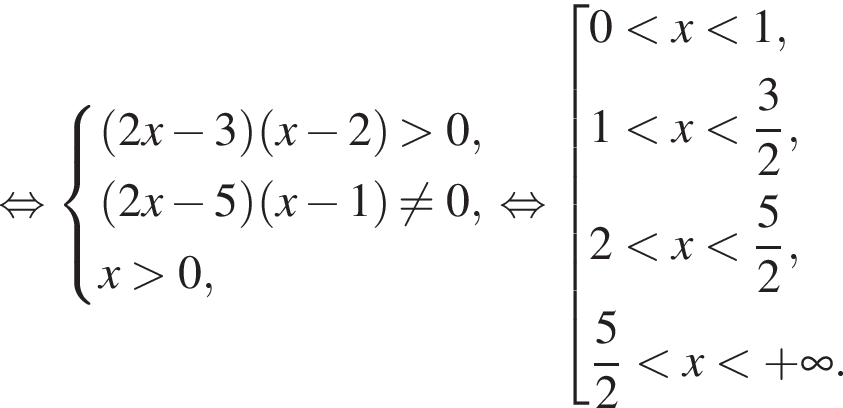


 Тогда
Тогда  откуда
откуда 
 Тогда
Тогда  откуда
откуда  то есть
то есть  или
или 


 определено при
определено при  поэтому неравенство записывается в виде
поэтому неравенство записывается в виде
 тогда
тогда











 тогда
тогда





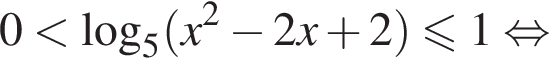










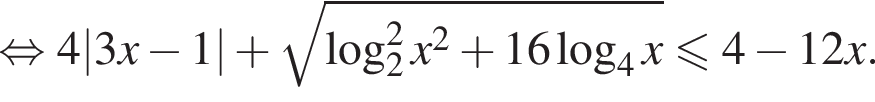
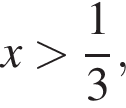 то
то

 то
то













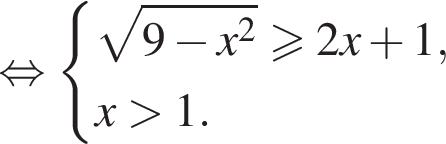
 получаем:
получаем:

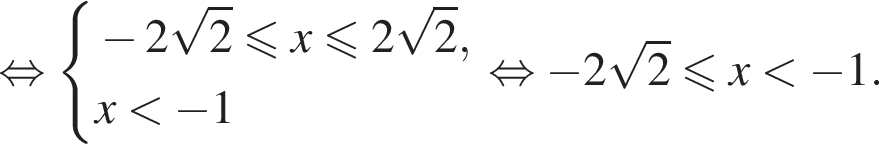





 получаем:
получаем:






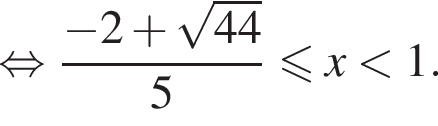
 получаем:
получаем: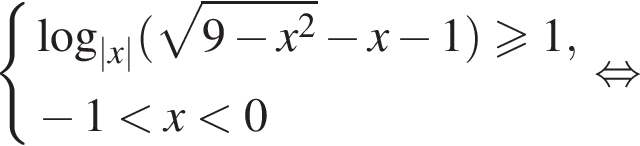




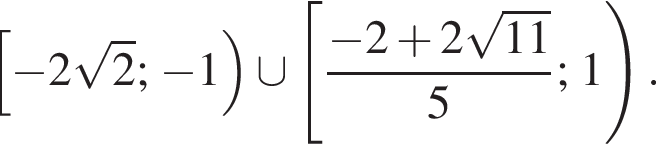
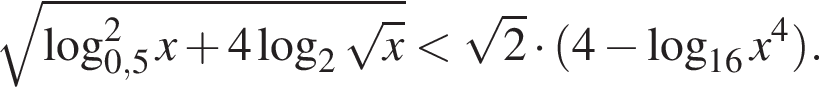


 тогда
тогда














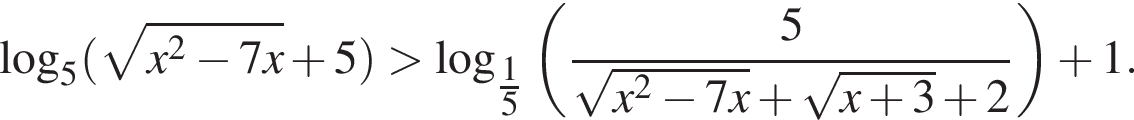





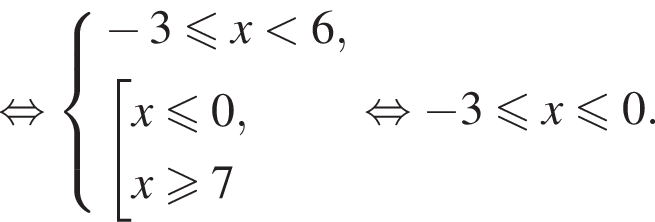
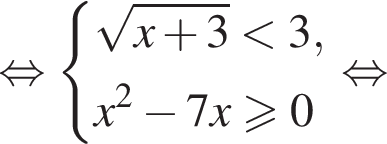









 то есть
то есть 















 а потому
а потому


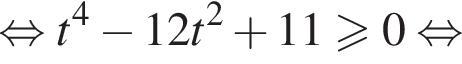










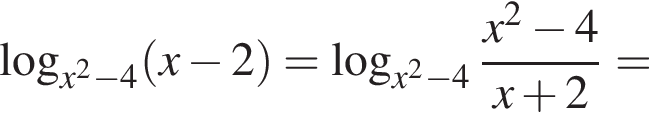



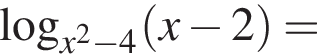

 тогда
тогда









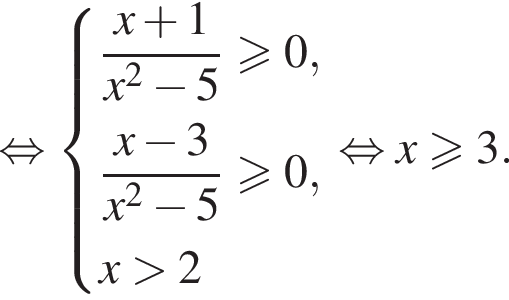







 тогда исходное неравенство примет вид:
тогда исходное неравенство примет вид:
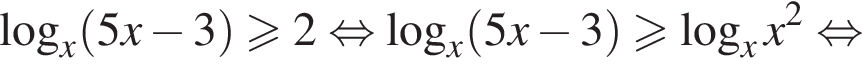






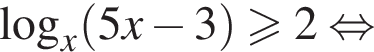





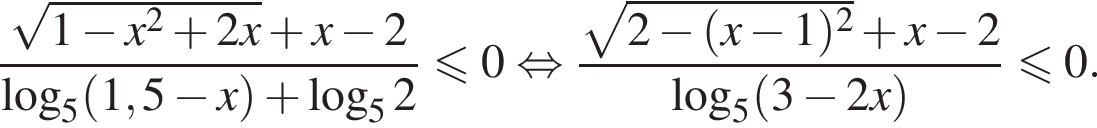





 получаем:
получаем: 
 получаем:
получаем:
 получаем:
получаем: 
 или
или 


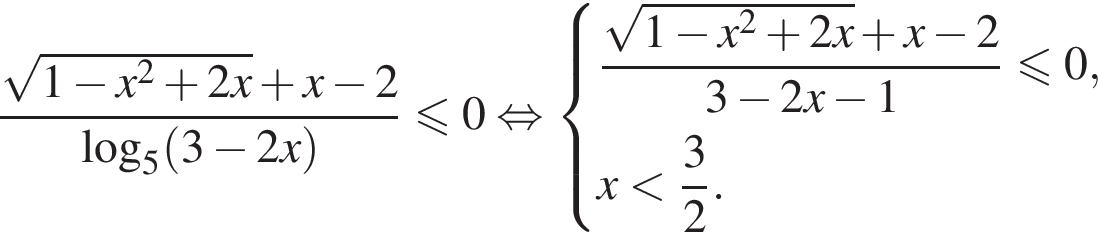
 Тогда получим
Тогда получим




 тогда
тогда






