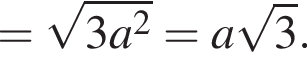Пятиугольник ABCDE вписан в окружность. Из вершины A опущены перпендикуляры AF, AH, AP и AQ на прямые DE, BE, CD и BC соответственно.
а) Докажите, что 
б) Найдите AH, если  и
и 
Решение. а) Будем пока считать, что F и Q лежат на продолжениях DE и CB соответственно а остальные точки — на отрезках. Тогда четырехугольники FEHA и APCQ вписанные (имеют по два противоположных прямых угла), откуда





что и требовалось.
Пусть теперь Q лежит на продолжении CB, а остальные точки — на отрезках. Тогда четырехугольники FEHA и APCQ вписанные (имеют два противоположных прямых угла и два равных прямых угла между стороной и диагональю первый), откуда 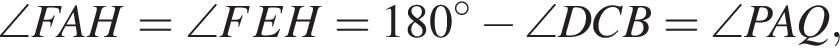 что и требовалось.
что и требовалось.
Аналогично разбираются остальные случаи расположения точек.
б) Углы QCA и HEA равны как вписанные углы, опирающиеся на одну дугу AB, поэтому прямоугольные треугольники CQA и AHE подобны. Углы AEF и ACP равны, поскольку оба они в сумме с углом AED дают 180°. Следовательно, подобны прямоугольные треугольники AFE и APC. Тогда верны пропорции  и
и  Разделим первую на вторую, получим
Разделим первую на вторую, получим  откуда
откуда 
Ответ: ![]()
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) ИЛИ имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) ИЛИ при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | 1 |
| Решение не соответствует ни одному из критериев, приведённых выше | 0 |
| Максимальный балл | 3 |






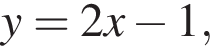 уравнение прямой BE:
уравнение прямой BE:  Координаты точки O найдём из системы уравнений
Координаты точки O найдём из системы уравнений 


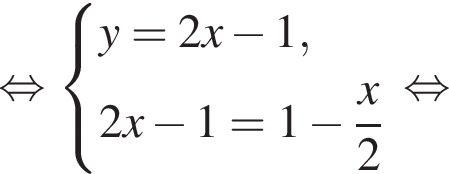

 и
и  равно
равно 
 то есть на хорды AO и AB описанной около четырёхугольника ABOK окружности опираются равные углы. Таким образом,
то есть на хорды AO и AB описанной около четырёхугольника ABOK окружности опираются равные углы. Таким образом, 



 Значит, скалярное произведение равно нулю, а тогда
Значит, скалярное произведение равно нулю, а тогда



 По теореме Пифагора из треугольника DCK находим:
По теореме Пифагора из треугольника DCK находим: 
 откуда
откуда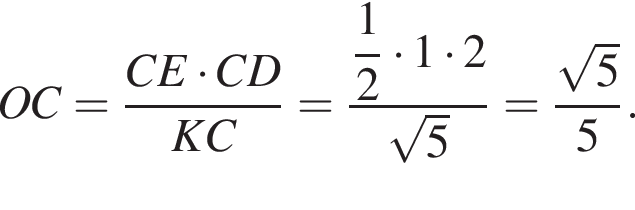








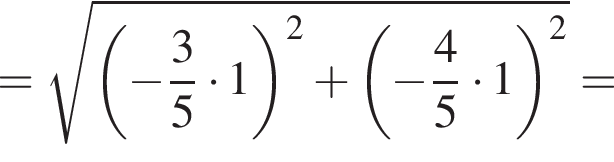


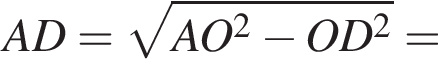
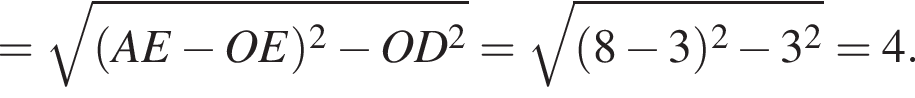





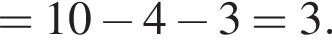
 Тогда
Тогда  Из треугольника N2M2B получаем, что
Из треугольника N2M2B получаем, что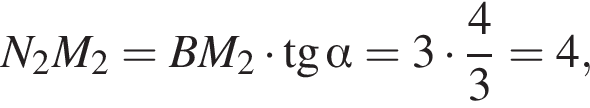

 Тогда
Тогда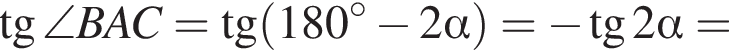













 Из этих двух равенств получаем, что
Из этих двух равенств получаем, что 




 тогда
тогда  и
и  По теореме косинусов
По теореме косинусов
 и
и 
 и
и  Из свойства хорд
Из свойства хорд  находим:
находим:







 то есть
то есть 








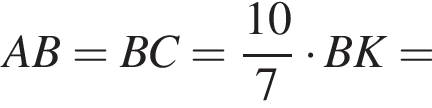





 и
и  тогда четырёхугольник POQC вписан в окружность. По тереме синусов
тогда четырёхугольник POQC вписан в окружность. По тереме синусов  следовательно, точка O лежит на биссектрисе угла ACB, то есть на прямой CN.
следовательно, точка O лежит на биссектрисе угла ACB, то есть на прямой CN. Треугольники APT, QBR и ABC подобны, значит,
Треугольники APT, QBR и ABC подобны, значит,
 и
и  Найдем гипотенузу AB:
Найдем гипотенузу AB: 









 Четырехугольник BCDM — параллелограмм, поэтому
Четырехугольник BCDM — параллелограмм, поэтому  Таким образом,
Таким образом,  а потому треугольник DEM равнобедренный, откуда следует, что углы DEM и DME равны. Углы DME и BMA также равны как вертикальные. Углы DEM и BAM равны, так как опираются на одну дугу. Следовательно, треугольник BMA равнобедренный, а потому
а потому треугольник DEM равнобедренный, откуда следует, что углы DEM и DME равны. Углы DME и BMA также равны как вертикальные. Углы DEM и BAM равны, так как опираются на одну дугу. Следовательно, треугольник BMA равнобедренный, а потому 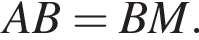 Треугольники BMA и DEM подобны по двум равным углам, а значит,
Треугольники BMA и DEM подобны по двум равным углам, а значит,




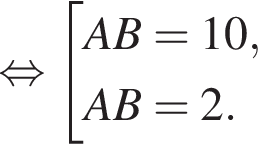
 то неравенство
то неравенство  для треугольника ABM не выполняется, поэтому
для треугольника ABM не выполняется, поэтому 



 и
и 
 Четырехугольник BCDM — параллелограмм, поэтому
Четырехугольник BCDM — параллелограмм, поэтому  а потому треугольник DEM равнобедренный. Отсюда следует, что углы DEM и DME равны. Углы DME и BMA также равны как вертикальные. Углы DEM и BAM равны, так как опираются на одну дугу. Следовательно, треугольник BMA равнобедренный, а потому
а потому треугольник DEM равнобедренный. Отсюда следует, что углы DEM и DME равны. Углы DME и BMA также равны как вертикальные. Углы DEM и BAM равны, так как опираются на одну дугу. Следовательно, треугольник BMA равнобедренный, а потому 





 то неравенство
то неравенство  не выполняется, поэтому
не выполняется, поэтому 


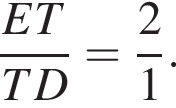 Площадь треугольника BOM равна
Площадь треугольника BOM равна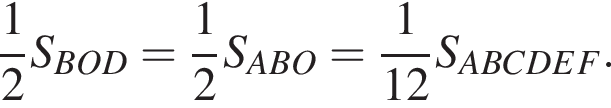







 BE = 2BC. По теореме косинусов для треугольника CDT получим, что
BE = 2BC. По теореме косинусов для треугольника CDT получим, что


 Тем самым
Тем самым
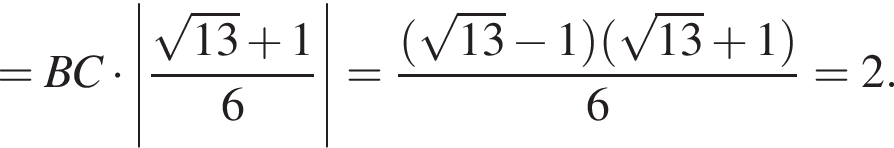
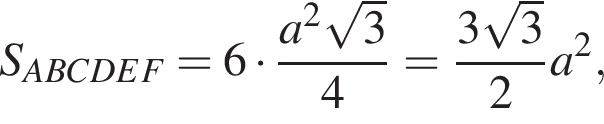

 то
то  значит, точка P — середина ребра EF. Следовательно, точка K — точка пересечения медиан треугольника AFE. Пусть также точка L — середина отрезка AE, тогда
значит, точка P — середина ребра EF. Следовательно, точка K — точка пересечения медиан треугольника AFE. Пусть также точка L — середина отрезка AE, тогда




 и
и 





 и
и  Тогда по теореме косинусов в треугольнике ABT:
Тогда по теореме косинусов в треугольнике ABT:
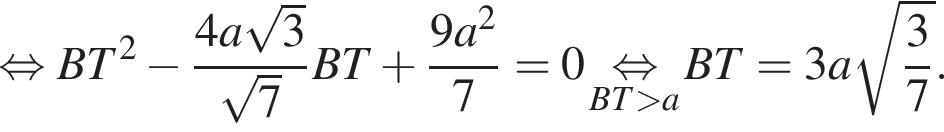


 и
и