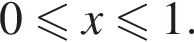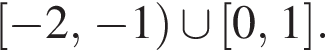1. Тип 15 № 507582 
Классификатор алгебры: Неравенство, содержащее радикал
Методы алгебры: Выделение полного квадрата, Метод интервалов
Кодификатор ФИПИ/Решу ЕГЭ: 2.2.9 Метод интервалов
Неравенства. Неравенства, содержащие радикалы
i
Решите неравенство 
Решение. Решение неравенства ищем при условиях: 
откуда 
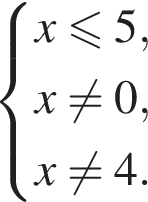
Рассмотрим два случая:
1) 
т. е. 
и, значит, 
или 
Таким образом, — решение задачи.
2) 
Разделив обе части неравенства на 
получим: 
откуда 
Решим это неравенство, получим: 
или 
Учитывая ограничения, получаем множество решений исходного неравенства: 
Ответ:
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 2 |
| Обоснованно получен ответ, отличающийся от верного исключением точек, ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Ответ:
507582
Классификатор алгебры: Неравенство, содержащее радикал
Методы алгебры: Выделение полного квадрата, Метод интервалов
Кодификатор ФИПИ/Решу ЕГЭ: 2.2.9 Метод интервалов
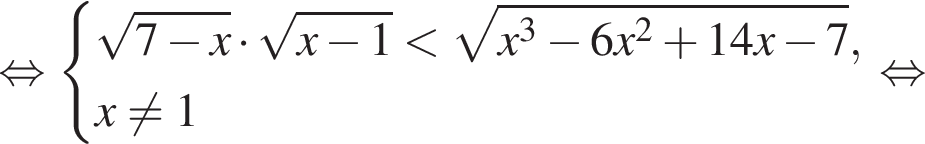
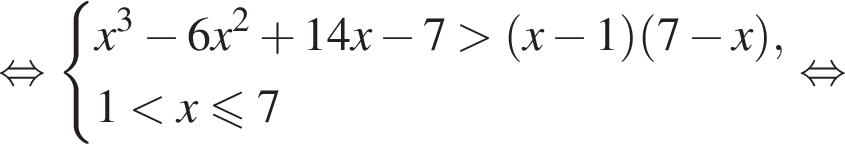
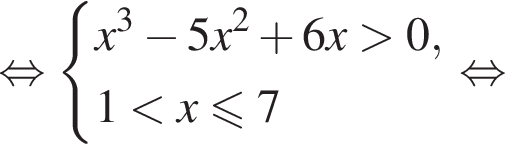
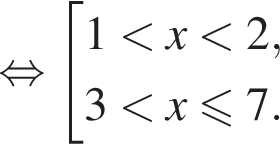
При этом условие 
избыточно, поскольку величина, большая неотрицательной, заведомо положительна. Существенным моментом решения является хорошее понимание этого обстоятельства. Именно поэтому, решая неравенство 
нет необходимости дополнительно решать неравенство 
Получаем систему неравенств: 
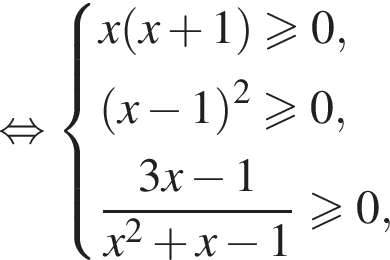
или 
или 
Тогда 
и неравенство равносильно неравенству 
Решим систему:
также является решением.
то 
или 
При этих значениях x выражение 
имеет смысл, поэтому 
являются решениями неравенства.
то 
при этом 
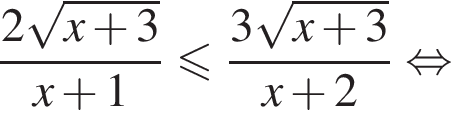
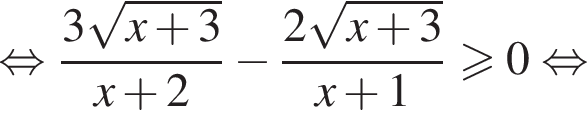
Тогда
и учитывая, что точки 0 и 6 также входят в являются решениями неравенства, получим множество решений исходного неравенства: 
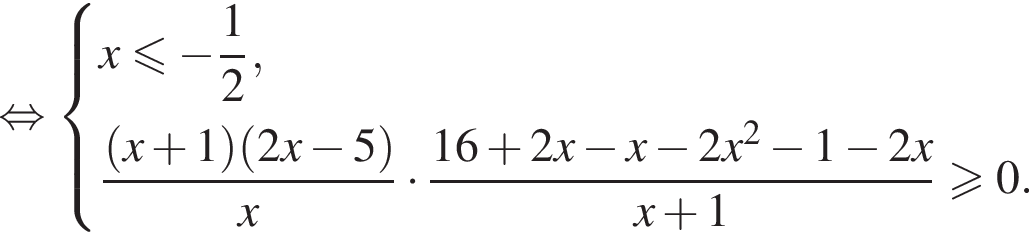
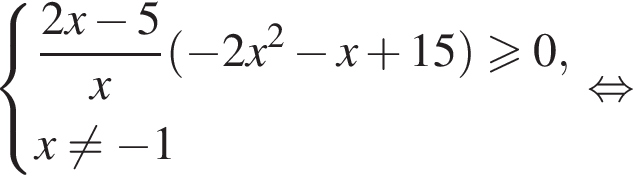
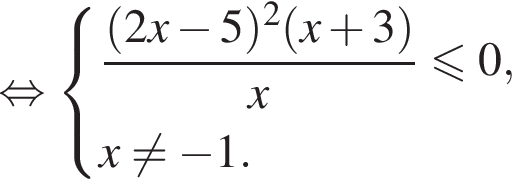
получаем решение: 
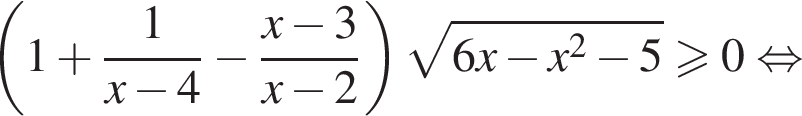
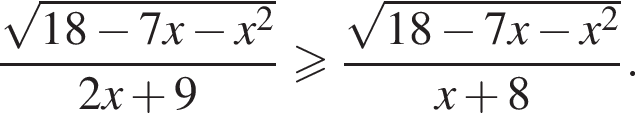
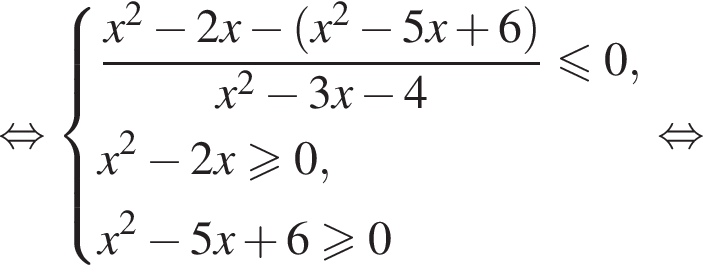
подкоренное выражение отрицательно, значит, решений нет. Пусть 
тогда:
выражение 
откуда x = 0 или x = 4.
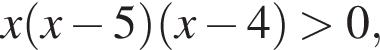выражение 
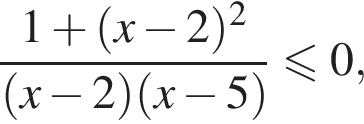то есть 
Получаем 
принимает только положительные значения. Найдем корни числителя при условии 
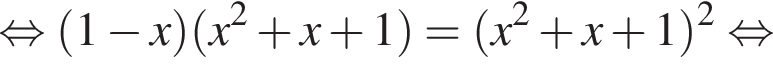
или 
